2.3.3专题二: 初速度为零的匀变速直线运动的规律及拓展 课件 (共30张PPT) -高一上学期物理人教版(2019)必修第1册
文档属性
| 名称 | 2.3.3专题二: 初速度为零的匀变速直线运动的规律及拓展 课件 (共30张PPT) -高一上学期物理人教版(2019)必修第1册 |  | |
| 格式 | pptx | ||
| 文件大小 | 13.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-29 11:15:14 | ||
图片预览











文档简介
(共30张PPT)
专题二: 初速度为零的匀变速直线运动的规律及拓展
第二章、匀变速直线运动的研究
初速度为零的匀变速直线运动等分位移规律
02
初速度为零的匀变速直线运动等分时间规律
01
方法与技巧
03
一题多解
04
巩固提升练习
05
匀变速直线运动
基本公式
重要推论
还有没有其他可循的规律呢?
初速度为零的匀变速直线运动等分时间规律
1. 求1T末、2T末、3T末……nT末的瞬时速度之比:
T
T
T
一、等分时间中的末速度之比
2.求前1T内、前2T内、前3T内……前nT内的位移之比:
T
T
T
x1
x2
x3
二、等分时间中的累加位移之比
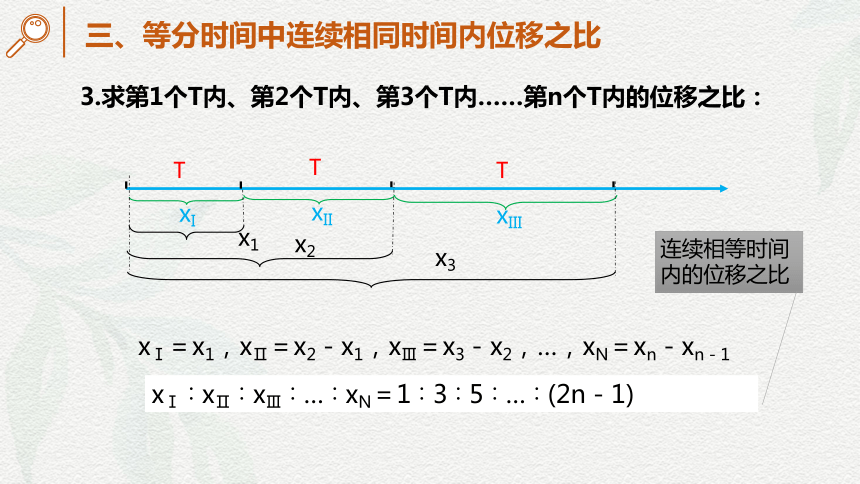
xⅠ=x1,xⅡ=x2-x1,xⅢ=x3-x2,…,xN=xn-xn-1
xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2n-1)
3.求第1个T内、第2个T内、第3个T内……第n个T内的位移之比:
T
T
T
xI
xII
xIII
x2
x1
x3
连续相等时间内的位移之比
三、等分时间中连续相同时间内位移之比
初速度为零的匀变速直线运动等分位移规律
1.求x末、2x末、3x末、…、nx末的瞬时速度之比:
x
x
x
一、等分位移中的末速度之比
2.求前1x内、前2x内、前3x内……前nx内的时间之比:
x
x
x
二、等分位移中的累加位移时间之比
3.求通过第1个x、第2个x、第3个x、…,第n个x所用的时间之比:
x
x
x
T1=t1, t2=T2-T1, t3=T3-T2 …,tN=Tn-Tn-1
三、等分位移中的连续相同位移内的时间之比
方法与技巧
解匀变速直线运动问题的常用方法
1、末速度为零的匀减速直线运动是初速度为零、加速度大小相等的反向匀加速直线运动的逆向运动。设物体的初速度为v0,加速度大小为a,做匀减速直线运动至速度为零,则可将此运动逆向看成初速度为0、加速度大小为 a 的匀加速直线运动,末速度为v0。
2、逆向思维法可简化问题的处理过程,但要注意原过程与逆过程的速度、位移的大小相等,但方向相反。
逆向思维法
一画:根据题意画出物体的运动示意图,使运动过程直观清晰。
二选:从以上常用方法中选取合适的方法。
三注意:注意列运动学方程时,方程式中每一个物理量均对应同一运动过程。
一画、二选、三注意
分析匀变速直线运动问题的技巧
【例题】如图所示,一物体以一定的初速度冲上固定的光滑斜面,斜面总长度为l,到达斜面最高点C时速度恰好为零,该过程物体做匀减速直线运动。已知物体第一次运动到距斜面底端 处的B点时,所用时间为 t,求物体从B滑到C所用的时间。
情境练习
一题多解
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面。故
又由以上三式解得 tBC=t
解法一:逆向思维法
因为物体沿斜面向上做匀减速直线运动,设物体从B滑到C所用的时间为tBC ,由匀变速直线运动的规律可得 ① ② ③
由①②③解得 ④
又vB=v0-at ⑤ vB=atBC ⑥
由④⑤⑥解得 tBC=t
解法二:基本公式法
对于初速度为零的匀加速直线运动,在连续相等的时间里通过的位移之比为x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)
因为
而通过xBA的时间为 t,所以通过xBC的时间tBC=t
解法三:位移比例法
对于初速度为零的匀加速直线运动,通过连续相等的各段位移所用的时间之比为
现将整个斜面分成相等的四段,如图所示,设通过BC段的时间为tx,那么通过BD、DE、EA的时间分别为
又tBD+tDE+tEA=t,解得tx=t
解法四:时间比例法
利用推论:中间时刻的瞬时速度等于这段位移的平均速度,
得
又
由以上三式解得
因为
所以有tBC=t
解法五:中间时刻速度法
根据匀变速直线运动的规律,作出v t图像,如图所示。利用相似三角形的规律,面积之比等于对应边长平方之比,
得 且
OD=t,OC=t+tBC。所以
解得tBC=t
解法六:图像法
1、1T末、2T末……瞬时速度比:
2、前1T内、前2T内……位移比:
xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2n-1)
3、第1个T内、第2个T内……位移比:
4、x末、2x末……瞬时速度比:
5、前1x内、前2x内……时间比:
6、第1个x、第2个x……时间比:
相等时间
相等位移
巩固提升
【练习1】第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕,其中滑雪是冬奥会中的一个比赛大项。如图所示,某滑雪运动员以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度为零。已知运动员在前四分之三位移中的平均速度大小为v,则滑雪者整个过程的平均速度为( )
A. B. C. D.
【正确答案】D
【练习2】取一根长2m左右的细线,5个铁垫圈和一个金属盘。在线下端系上第一个垫圈1,隔12 cm再系一个垫圈2,以后垫圈之间的距离分别为36 cm、60 cm、84 cm,如图所示。站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地上的金属盘。松手后开始计时,若不计空气阻力,则第2、3、4、5个垫圈( )
A.落到盘上的时间间隔越来越大
B.落到盘上的时间间隔越来越小
C.依次落到盘上的时间关系为1∶2∶3∶4
D.依次落到盘上的时间关系为
【正确答案】C
【练习3】第24届北京“冬奥会”于2022年2月4日由北京市和张家口市联合举办。在“冬奥会”冰上项目中冰壶比赛是极具观赏性的一个项目。如图所示,在一次训练中,冰壶(可视为质点)以某一速度沿虚线做匀减速直线运动,垂直进入四个完全相同的矩形区域,离开第四个矩形区域边缘的E点时速度恰好为零。冰壶从A点运动到D点和从B点运动到E点的时间分别为t1和t2,则t1与t2之比为( )
A. B. C. D.
【正确答案】A
【练习4】如图所示,音乐喷泉竖直向上喷出水流,喷出的水经3s到达最高点,把最大高度分成三等份,水通过起始的第一等份用时为t1,通过最后一等份用时为t2。空气阻力不计,则 满足( )
A. B.
C. D.
【正确答案】B
【练习5】如图所示,光滑斜面AE被分为四个相等的部分,一物体从A点由静止释放,它沿斜面向下做匀加速运动,依次通过B、C、D点,最后到达底端E点。下列说法正确的是( )
A.物体通过各点的瞬时速度之比为vB∶vC∶vD∶vE=1∶2∶3∶4
B.通过各段所用的时间之比为tAB∶tBC∶tCD∶tDE=1∶ ∶ ∶2
C.物体由A点到各点所经历的时间之比为tB∶tC∶tD∶tE=1∶ ∶ ∶2
D.下滑全程的平均速度
【正确答案】C
专题二: 初速度为零的匀变速直线运动的规律及拓展
第二章、匀变速直线运动的研究
初速度为零的匀变速直线运动等分位移规律
02
初速度为零的匀变速直线运动等分时间规律
01
方法与技巧
03
一题多解
04
巩固提升练习
05
匀变速直线运动
基本公式
重要推论
还有没有其他可循的规律呢?
初速度为零的匀变速直线运动等分时间规律
1. 求1T末、2T末、3T末……nT末的瞬时速度之比:
T
T
T
一、等分时间中的末速度之比
2.求前1T内、前2T内、前3T内……前nT内的位移之比:
T
T
T
x1
x2
x3
二、等分时间中的累加位移之比
xⅠ=x1,xⅡ=x2-x1,xⅢ=x3-x2,…,xN=xn-xn-1
xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2n-1)
3.求第1个T内、第2个T内、第3个T内……第n个T内的位移之比:
T
T
T
xI
xII
xIII
x2
x1
x3
连续相等时间内的位移之比
三、等分时间中连续相同时间内位移之比
初速度为零的匀变速直线运动等分位移规律
1.求x末、2x末、3x末、…、nx末的瞬时速度之比:
x
x
x
一、等分位移中的末速度之比
2.求前1x内、前2x内、前3x内……前nx内的时间之比:
x
x
x
二、等分位移中的累加位移时间之比
3.求通过第1个x、第2个x、第3个x、…,第n个x所用的时间之比:
x
x
x
T1=t1, t2=T2-T1, t3=T3-T2 …,tN=Tn-Tn-1
三、等分位移中的连续相同位移内的时间之比
方法与技巧
解匀变速直线运动问题的常用方法
1、末速度为零的匀减速直线运动是初速度为零、加速度大小相等的反向匀加速直线运动的逆向运动。设物体的初速度为v0,加速度大小为a,做匀减速直线运动至速度为零,则可将此运动逆向看成初速度为0、加速度大小为 a 的匀加速直线运动,末速度为v0。
2、逆向思维法可简化问题的处理过程,但要注意原过程与逆过程的速度、位移的大小相等,但方向相反。
逆向思维法
一画:根据题意画出物体的运动示意图,使运动过程直观清晰。
二选:从以上常用方法中选取合适的方法。
三注意:注意列运动学方程时,方程式中每一个物理量均对应同一运动过程。
一画、二选、三注意
分析匀变速直线运动问题的技巧
【例题】如图所示,一物体以一定的初速度冲上固定的光滑斜面,斜面总长度为l,到达斜面最高点C时速度恰好为零,该过程物体做匀减速直线运动。已知物体第一次运动到距斜面底端 处的B点时,所用时间为 t,求物体从B滑到C所用的时间。
情境练习
一题多解
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面。故
又由以上三式解得 tBC=t
解法一:逆向思维法
因为物体沿斜面向上做匀减速直线运动,设物体从B滑到C所用的时间为tBC ,由匀变速直线运动的规律可得 ① ② ③
由①②③解得 ④
又vB=v0-at ⑤ vB=atBC ⑥
由④⑤⑥解得 tBC=t
解法二:基本公式法
对于初速度为零的匀加速直线运动,在连续相等的时间里通过的位移之比为x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)
因为
而通过xBA的时间为 t,所以通过xBC的时间tBC=t
解法三:位移比例法
对于初速度为零的匀加速直线运动,通过连续相等的各段位移所用的时间之比为
现将整个斜面分成相等的四段,如图所示,设通过BC段的时间为tx,那么通过BD、DE、EA的时间分别为
又tBD+tDE+tEA=t,解得tx=t
解法四:时间比例法
利用推论:中间时刻的瞬时速度等于这段位移的平均速度,
得
又
由以上三式解得
因为
所以有tBC=t
解法五:中间时刻速度法
根据匀变速直线运动的规律,作出v t图像,如图所示。利用相似三角形的规律,面积之比等于对应边长平方之比,
得 且
OD=t,OC=t+tBC。所以
解得tBC=t
解法六:图像法
1、1T末、2T末……瞬时速度比:
2、前1T内、前2T内……位移比:
xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2n-1)
3、第1个T内、第2个T内……位移比:
4、x末、2x末……瞬时速度比:
5、前1x内、前2x内……时间比:
6、第1个x、第2个x……时间比:
相等时间
相等位移
巩固提升
【练习1】第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕,其中滑雪是冬奥会中的一个比赛大项。如图所示,某滑雪运动员以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度为零。已知运动员在前四分之三位移中的平均速度大小为v,则滑雪者整个过程的平均速度为( )
A. B. C. D.
【正确答案】D
【练习2】取一根长2m左右的细线,5个铁垫圈和一个金属盘。在线下端系上第一个垫圈1,隔12 cm再系一个垫圈2,以后垫圈之间的距离分别为36 cm、60 cm、84 cm,如图所示。站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地上的金属盘。松手后开始计时,若不计空气阻力,则第2、3、4、5个垫圈( )
A.落到盘上的时间间隔越来越大
B.落到盘上的时间间隔越来越小
C.依次落到盘上的时间关系为1∶2∶3∶4
D.依次落到盘上的时间关系为
【正确答案】C
【练习3】第24届北京“冬奥会”于2022年2月4日由北京市和张家口市联合举办。在“冬奥会”冰上项目中冰壶比赛是极具观赏性的一个项目。如图所示,在一次训练中,冰壶(可视为质点)以某一速度沿虚线做匀减速直线运动,垂直进入四个完全相同的矩形区域,离开第四个矩形区域边缘的E点时速度恰好为零。冰壶从A点运动到D点和从B点运动到E点的时间分别为t1和t2,则t1与t2之比为( )
A. B. C. D.
【正确答案】A
【练习4】如图所示,音乐喷泉竖直向上喷出水流,喷出的水经3s到达最高点,把最大高度分成三等份,水通过起始的第一等份用时为t1,通过最后一等份用时为t2。空气阻力不计,则 满足( )
A. B.
C. D.
【正确答案】B
【练习5】如图所示,光滑斜面AE被分为四个相等的部分,一物体从A点由静止释放,它沿斜面向下做匀加速运动,依次通过B、C、D点,最后到达底端E点。下列说法正确的是( )
A.物体通过各点的瞬时速度之比为vB∶vC∶vD∶vE=1∶2∶3∶4
B.通过各段所用的时间之比为tAB∶tBC∶tCD∶tDE=1∶ ∶ ∶2
C.物体由A点到各点所经历的时间之比为tB∶tC∶tD∶tE=1∶ ∶ ∶2
D.下滑全程的平均速度
【正确答案】C
