浙江省2024年秋季九年级上册第一次月考数学检测卷 含解析
文档属性
| 名称 | 浙江省2024年秋季九年级上册第一次月考数学检测卷 含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 12:28:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省2024年秋季九年级上册第一次月考数学检测卷
范围:第1-3章 满分:120分 时间:120分钟
题号 选择题 填空题 解答题
得分
一.选择题(共10小题,满分30分,每小题3分)
1.二次函数y=x2+2x+1的顶点坐标为( )
A.(﹣1,0) B.(1,0) C.(0,﹣1) D.(0,1)
2.为了丰富校园生活,培养学生特长,学校开展了特色课程.小明从感兴趣的“花样跳绳”“天文地理”“艺术插花”“象棋博交”4门课程中随机选择一门学习.小明选中“天文地理”这一门课程的概率为( )
A. B. C. D.
3.如图,将△AOB绕点O按逆时针方向旋转50°后得到△COD,若∠AOB=20°,则∠AOD的度数是( )
A.20° B.30° C.40° D.50°
4.如图,AB是圆O的直径,CD是圆O的弦,∠ABD=69°,则∠C等于( )
A.29° B.21° C.31° D.62°
5.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.36左右,则布袋中黄球估计有( )
A.18个 B.22个 C.28个 D.32个
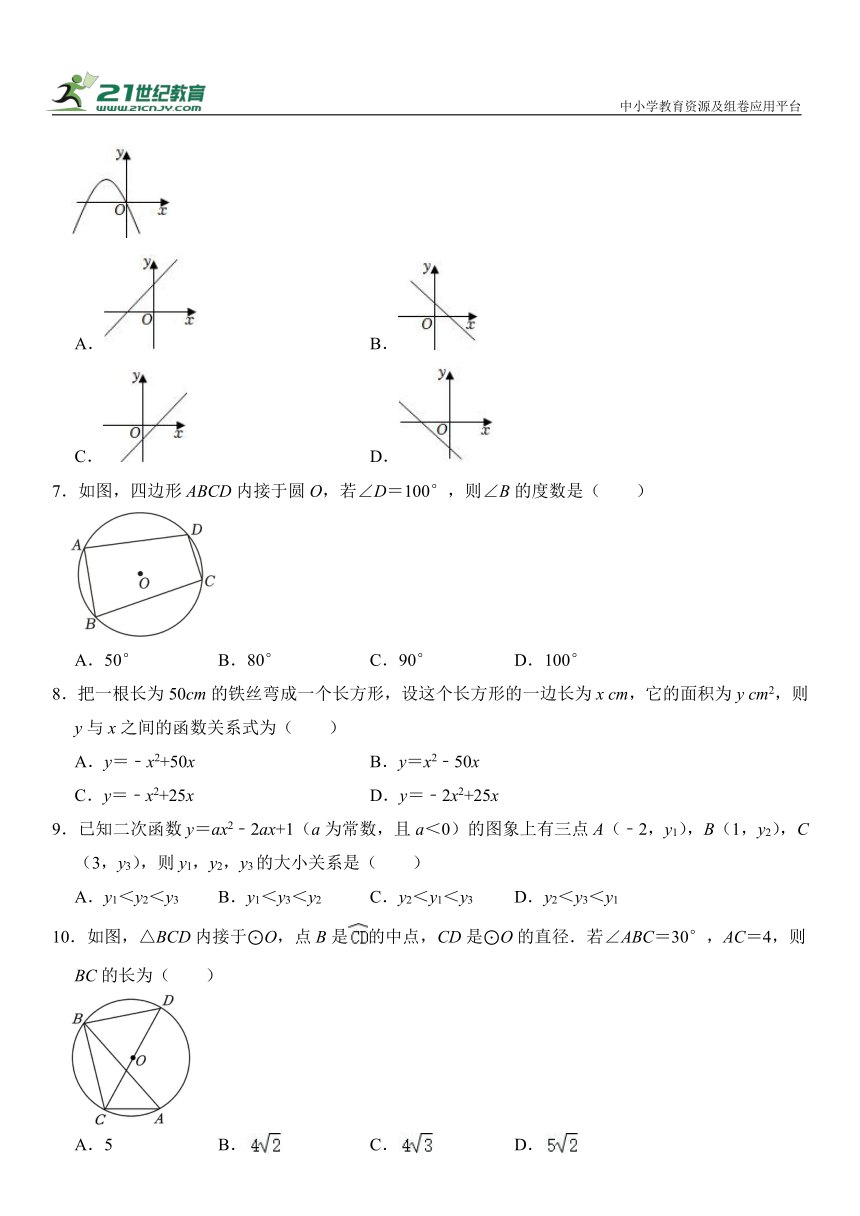
6.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=﹣ax+b的图象大致是( )
A. B.
C. D.
7.如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是( )
A.50° B.80° C.90° D.100°
8.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x cm,它的面积为y cm2,则y与x之间的函数关系式为( )
A.y=﹣x2+50x B.y=x2﹣50x
C.y=﹣x2+25x D.y=﹣2x2+25x
9.已知二次函数y=ax2﹣2ax+1(a为常数,且a<0)的图象上有三点A(﹣2,y1),B(1,y2),C(3,y3),则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y1<y3 D.y2<y3<y1
10.如图,△BCD内接于⊙O,点B是的中点,CD是⊙O的直径.若∠ABC=30°,AC=4,则BC的长为( )
A.5 B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.写出一个开口向下,顶点为(1,2)的二次函数 .
12.已知⊙O的半径为5,点P在⊙O上,则OP的长为 .
13.某商场为吸引顾客设计了如图所示的自由转盘,当指针指向阴影部分(含边界)时,该顾客可获奖品一份,那么该顾客获奖的概率为 .
14.将抛物线y=﹣2(x+2)2向右平移3个单位长度,再向下平移4个单位长度得到的抛物线的函数解析式为 .
15.如图,已知⊙O的内接正六边形ABCDEF的边长为4,H为边AF的中点,则图中阴影部分的面积是 .
16.已知二次函数y=ax2+bx+c的图象经过(1,0),(﹣2,t)两点,其中t<0,对称轴为x=﹣1.下列四个结论:①bc<0;②c=t;③点A(s,y1)、B(s+1,y2)在抛物线上,当s<﹣1时,y1>y2;④已知关于x的方程ax2+bx+c﹣m=0(m>0)有两个根,其中一个根是3,若关于x的方程ax2+bx+c﹣n=0(0<n<m)有整数根,则其根为﹣4和2;其中正确的结论是 (填写序号).
三.解答题(共8小题,满分72分)
17.(7分)如图,已知⊙O内接ABC,AD为⊙O直径,AE⊥BC于E点,连接BD.求证:∠BAD=∠CAE.
18.(7分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕O顺时针旋转90°后的△A2B2C2并写出点C2的坐标.
19.(8分)如图,一座石桥的主桥拱是圆弧形,某时刻测得水面AB的宽度为8m,拱高CD(的中点到水面的距离)为2m.
(1)求所在圆的半径;
(2)若水面下降1m,求此时水面的宽度(保留根号).
20.(8分)从背面相同的同一副扑克牌中取出9张红桃,10张黑桃,11张方块.
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉9张红桃和m(m>6)张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,再从桌面上随机抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
21.(8分)【探究】如图,已知抛物线y=﹣x2+4.
(1)在坐标系中画出此抛物线y的大致图象(不要求列表);
(2)该抛物线y=﹣x2+4可由抛物线y=﹣x2向 平移 个单位得到;
(3)当﹣1≤x≤3时,函数值y取值范围是 .
【应用】已知二次函数y=﹣(x﹣h)2(h是常数),且自变量取值范围是2≤x≤5.
(1)当h=3时,求函数的最大值;
(2)若函数的最大值为﹣1,求h的值.
22.(10分)排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生在O处将球垫偏,之后又在A、B两处先后垫球,球沿抛物线C1→C2→C3运动(假设抛物线C1、C2、C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点,点B的横坐标为,抛物线C1表达式为y=ax2﹣2ax和抛物线C3表达式为y=2ax2+bx(a≠0).
(1)求抛物线C1的函数表达式;
(2)第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;
(3)为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处B离地面的高度至少为多少米?
23.(12分)如图,在△ABC中,∠C=90°,点M在圆O上,AC交圆O于点M,BC与圆O交于点D,DM=DE,DE⊥AD交AB于点E,AE为⊙O的直径,DF⊥AB.
(1)求证:∠CAD=∠DAB;
(2)若DM平分∠ADC,求∠CAD的度数;
(3)若AD=BD=6cm,求图中阴影部分的面积.
24.(12分)如图,抛物线y=ax2+bx﹣4交x轴于点A(﹣2,0)和点B(4,0),交y轴于点C.
(1)求抛物线的表达式;
(2)若点P是直线BC下方抛物线上一动点,连接PC,PB,当△PBC的面积最大时,求点P的坐标及面积的最大值;
(3)在(2)的条件下,若点N是直线BC上的动点,在平面内的是否存在点Q,使得以PB为边、以P、B、N、Q和顶点的四边形是菱形?若存在,请求出符合条件的所有Q点的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【分析】利用函数顶点式解答即可.
【解答】解:y=x2+2x+1=(x+1)2,
二次函数顶点坐标为(﹣1,0),
故选:A.
2.【分析】直接根据概率公式解答即可.
【解答】解:∵小明从感兴趣的“花样跳绳”“天文地理”“艺术插花”“象棋博交”4门课程中随机选择一门学习,
∴小明选中“天文地理”这一门课程的概率为.
故选:B.
3.【分析】首先根据旋转变换的性质求出∠BOD=50°,结合∠AOB=20°,即可解决问题.
【解答】解:由题意及旋转变换的性质得:∠BOD=50°,
∵∠AOB=20°,
∴∠AOD=50°﹣20°=30°,
故选:B.
4.【分析】首先根据同弧所对的圆周角相等求得角A的度数,然后再求得∠ABD的度数即可.
【解答】解:∵AB是直径,
∴∠ADB=90°,
∵∠ABD=69°,
∴∠A=21°,
∴∠C=21°,
故选:B.
5.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
【解答】解:设袋中有黄球x个,由题意得=0.36,
解得x=18,
∴黄球可能有18个.
故选:A.
6.【分析】可先根据二次函数的图象判断a、b的符号,再判断一次函数图象与实际是否相符,判断正误.
【解答】解:由二次函数图象,得出a<0,b<0,
A、一次函数图象,得a<0,b>0,故A错误;
B、一次函数图象,得a>0,b>0,故B错误;
C、一次函数图象,得a<0,b<0,故C正确;
D、一次函数图象,得a>0,b<0,故D错误;
故选:C.
7.【分析】根据圆内接四边形的性质得出∠A+∠C=180°,再代入求出答案即可.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠C=100°,
∴∠A=80°,
故选:B.
8.【分析】要求长方形的面积,需求出长方形相邻两边的长度,根据长方形的周长公式可计算出长方形另一边的长为(25﹣x)cm;接下来,根据长方形的面积公式即可得到y与x的函数关系式.
【解答】解:设这个长方形的一边长为x cm,周长是50cm,
∴另一边长是(25﹣x)cm,
∴y与x的函数关系式为:y=x(25﹣x)=﹣x2+25x.
选项A、B、D都不正确,选项C正确.
故选:C.
9.【分析】先确定对称轴,根据把点A的对称点确定,转化为对称轴同侧的点,根据抛物线开口向下,对称轴的右侧y随x的增大而减小即可得到解答.
【解答】解:∵二次函数y=ax2﹣2ax+1(a为常数,且a<0)的图象上有三点A(﹣2,y1),B(1,y2),C(3,y3),
∴对称轴.
设点A的对称点为(x0,y1),
所以.
解得x0=4,
∴点A的对称点为(4,y1).
∵a<0,
∴抛物线开口向下.
∴对称轴的右侧y随x的增大而增减小.
∵4>3>1,
所以y1<y3<y2.
故选:B.
10.【分析】连接OA,先根据圆周角定理可得∠AOC=2∠ABC=60°,从而可得△AOC是等边三角形,根据等边三角形的性质可得AC=OC=4,从而可得DC=2OC=8,然后根据直径所对的圆周角是直角可得∠CBD=90°,再根据已知可得=,从而可得CB=BD,最后根据等腰直角三角形的性质进行计算即可解答.
【解答】解:连接OA,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OC=4,
∴DC=2OC=8,
∵CD是⊙O的直径,
∴∠CBD=90°,
∵点B是的中点,
∴=,
∴CB=BD,
∴BC==4,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.【分析】因为顶点为(1,2),所以设y=a(x﹣1)2+2,因为开口向下,所以a<0,据此即可作答.
【解答】解:∵顶点为(1,2),
∴设二次函数的解析式y=a(x﹣1)2+2,
∵开口向下,
∴a=﹣1<0,
∴y=﹣(x﹣1)2+2,
故答案为:y=﹣(x﹣1)2+2(答案不唯一).
12.【分析】根据d=r时点在圆上解决问题即可.
【解答】解:∵⊙O的半径为5,点P在⊙O上,
∴OP=r=5.
故答案为:5.
13.【分析】先求出45°在整个转盘中所占面积的比值,根据此比值即可解答.
【解答】解:阴影部分占45°,
则其占整个圆面积的=,
即该顾客获奖的概率为.
故答案为:.
14.【分析】由平移的规律即可求得答案.
【解答】解:将抛物线y=﹣2(x+2)2向右平移3个单位,则函数解析式变为y=﹣2(x+2﹣3)2=﹣2(x﹣1)2,向下平移4个单位长度得到的抛物线的函数解析式为y=﹣2(x﹣1)2﹣4.
故答案为:y=﹣2(x﹣1)2﹣4.
15.【分析】根据题意先计算出S△CDH的面积,再计算扇形COD面积及S△COD面积,即可得到本题答案.
【解答】解:过点H作HE⊥CD交CD于点Q,连接OC,OD,
∵⊙O的内接正六边形ABCDEF的边长为4,H为边AF的中点,
∴∠COD=60°,∠QCO=60°,CO=OD=4,Q为边CD的中点,
∴CQ=DQ=2,
∴OQ=2,
∴QH=4,
∴,
∴扇形COD面积:,
∵,
∴阴影部分的面积:,
故答案为:.
16.【分析】利用二次函数的图象及性质,系数间的关系和一元二次方程的关系即可求解.
【解答】解:∵抛物线过(1,0),对称轴为x=﹣1,
∴图象必过(﹣3,0),
又∵过点(﹣2,t)(t<0),
∴开口向上,与y轴交于负半轴,
∴a>0,b>0,c<0,故①对;
∵(0,c)与(﹣2,t)到对称轴等距,
∴c=t,故②对;
∵s<﹣1,无法判断点A(s,y1)、B(s+1,y2)与对称轴是同侧还是异侧,
也就无法判断点A、B与对称轴x=﹣1的距离的大小,故无法比较y1与y2的大小,故③错;
∵方程ax2+bx+c=0的两根分别为1和﹣3,
又x的方程ax2+bx+c﹣m=0(m>0)有两个根,其中一个根是3,而抛物线的对称轴为x=﹣1,由对称性得另一个根为﹣5,
观察图象,得关于x的方程ax2+bx+c﹣n=0(0<n<m)整数根为﹣4和2,故④对,
故答案为:①②④.
三.解答题(共8小题,满分72分)
17.【分析】由圆周角定理,推出∠ABD=90°,∠D=∠C,由垂直的定义得到∠AEC=90°,由三角形内角和定理推出∠BAD=∠CAE.
【解答】证明:∵AD是圆的直径,
∴∠ABD=90°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠ABD=∠AEC,
∵∠D=∠C,
∴∠BAD=∠CAE.
18.【分析】(1)分别确定A,B,C关于原点的对称点A1,B1,C1,再顺次连接A1,B1,C1,可得答案;
(2)分别确定A,B,C绕原点O顺时针旋转90°后的对应点A2,B2,C2,再顺次连接A2,B2,C2,再根据C2的位置可得答案.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;C2(4,﹣3).
19.【分析】(1)根据垂径定理得到OC⊥AB,AC=BC,结合勾股定理求解即可得到答案;
(2)根据(1)即可得到OG=5﹣1﹣2=2m,OF=5m,结合勾股定理求解即可得到答案;
【解答】(1)解:如图,设所在圆的圆心为O,连接OA,OC,
∵D是的中点,CD⊥AB,即OD为圆的半径,
∴,
设OA=OD=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,OA2=OC2+AC2,
即r2=(r﹣2)2+42,解得r=5,故所在圆的半径为5m;
(2)解:如图,连接OF,设OD与EF交于点G,则∠OGF=90°,
在Rt△OGF中,OG=5﹣1﹣2=2(m),OF=5m,
∴,
∴,
故此时水面的宽度为.
20.【分析】(1)由概率公式计算即可;
(2)①事件“再抽出的这张牌是方块”为必然事件,则剩下的牌只有方块,即可得出答案;
②事件“再抽出的这张牌是方块”为随机事件,则剩下的牌有黑桃和方块,再由m>6和概率公式即可得出答案.
【解答】解:(1)从中随机抽出一张是红桃的概率是=;
(2)①∵事件“再抽出的这张牌是方块”为必然事件,则剩下的牌只有方块,
∴当m为10时,事件“再抽出的这张牌是方块”为必然事件,
②∵事件“再抽出的这张牌是方块”为随机事件,
∴剩下的牌有黑桃和方块,
∵m>6,
∴当m为9、8、7时,事件“再抽出的这张牌是方块”为随机事件事件,
这个事件的概率的最小值为:=.
21.【分析】探究(1)依据题意,函数为y=﹣x2+4,则抛物线开口向下,对称轴是y轴,顶点为(0,4),进而可以作图;
(2)依据题意,根据平移规律“上加下减,左加右减”,进而可以判断得解;
(3)依据题意,由抛物线为y=﹣x2+4,故当x=0时,y取最大值为4,结合当x=﹣1时,y=3;当x=3时,y=﹣5,进而可以判断得解;
应用(1)依据题意,由h=3,可得二次函数为:y=﹣(x﹣3)2,故当x=3时,函数有最大值为0,结合2≤x≤5,从而可以判断得解;
(2)依据题意,二次函数y=﹣(x﹣h)2(h为常数),当自变量x满足2≤x≤5时,其对应函数y的最大值为﹣1,进而分5<h、h<2和2<h<5分别进行计算分析可以得解.
【解答】解:探究(1)由题意,函数为y=﹣x2+4,
∴抛物线开口向下,对称轴是y轴,顶点为(0,4).
作图如下.
(2)由题意,∵抛物线为y=﹣x2+4,
又根据平移规律“上加下减,左加右减”,
∴抛物线为y=﹣x2+4可由y=﹣x2向上平移4个单位得到.
故答案为:4.
(3)由题意,∵抛物线为y=﹣x2+4,
∴当x=0时,y取最大值为4,
又当x=﹣1时,y=3;当x=3时,y=﹣5,
∴当﹣1≤x≤3时,﹣5≤y≤4.
故答案为:﹣5≤y≤4.
应用(1)由题意,∵h=3,
∴二次函数为:y=﹣(x﹣3)2.
∴当x=3时,函数有最大值为0.
∵2≤x≤5,
∴当x=3时,函数有最大值为0,符合题意.
(2)∵二次函数y=﹣(x﹣h)2(h为常数),当自变量x满足2≤x≤5时,其对应函数y的最大值为﹣1,
∴若5<h,则当x=5时,y最大,即﹣(5﹣h)2=﹣1,得h1=4(舍去),h2=6;
若h<2,则当x=2时,y最大,即﹣(2﹣h)2=﹣1,得h3=1,h4=3(舍去);
若2<h<5,则最大值为0,与题意不符;
由上可得,h的值是6或1.
22.【分析】(1)直接利用待定系数法,即可求出抛物线C1的函数表达式;
(2)将抛物线C1表达式化为顶点式,得到顶点坐标,求出实际最大高度,即可得到答案;
(3)由(1)可知,,得到抛物线C3表达式为y=﹣x2+bx,进而得到对称轴为直线,顶点坐标为,根据最大高度的要求和对称轴,求出b≤﹣2,再根据点B的横坐标为,得到,求出yB的最小值即可得到答案.
【解答】解:(1)∵抛物线C1表达式为y=ax2﹣2ax,且经过点,
∴,
解得:,
∴抛物线C1的函数表达式为:;
(2)最大高度未达到要求,理由如下:
由(1)得,抛物线C1的函数表达式为,
∵,
∴抛物线C1的顶点坐标为,
∵O处离地面的距离为1米,
∴球在运动中离地面的最大高度为,
∴最大高度未达到要求;
(3)解:由(1)可知,,
∵抛物线C3表达式为y=﹣x2+bx,
∴对称轴为直线,顶点坐标为,
∵球在运动中离地面的最大高度达到要求,
∴,
∴b≥2或b≤﹣2,
∵对称轴在x轴负半轴,
∴b<0,
∴b≤﹣2,
∵点B的横坐标为,
∴,
∴当b=﹣2时,yB有最小值,最小值为,
∴点B离地面的高度至少为(米).
23.【分析】(1)根据圆周角定理即可得出答案;
(2)由角平分线定义得到∠CDM=∠ADM,由等腰三角形的性质,余角的性质推出∠CDM=∠CAD,由直角三角形的性质即可求出∠CAD的度数;
(3)由等腰三角形的性质,直角三角形的性质求出∠B的度数,得到∠DOE=60°,由直角三角形的性质求出DF,OF,OD的长,求出扇形ODE的面积,△ODF的面积,即可求出阴影的面积.
【解答】(1)证明:∵DM=DE,
∴=,
∴∠CAD=∠DAB;
(2)解:连接OM,OD,作OH⊥MD于H,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠CAD=∠DAB,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90,
∴AC⊥BC,
∴OD⊥BC,
∴∠MDC+∠MDO=90°,
∵OM=OD,OH⊥MD,
∴∠DOH=∠MOD,
∵∠CAD=∠MOD,
∴∠CAD=∠DOH,
∵∠DOH+∠MDO=90°,
∴∠DOH=∠CDM,
∴∠CAD=∠CDM,
∵DM平分∠ADC,
∴∠CDM=∠ADM,
∵∠CAD+∠ADM+∠CDM=90°,
∴∠CAD=30°;
(3)解:∵DA=DB,
∴∠DAB=∠B,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠DOB=∠DAB+∠ADO=2∠B,
∵∠DOB+∠B=90°,
∴∠B=∠DAB=30°,
∴∠BOD=60°,
∵AD=6cm,
∴DF=AD=3cm,
∴OF=FD=cm,
∴OD=2OF=2cm,
∴扇形ODE的面积==2π(cm2),△ODF的面积=OF DF=×3×=(cm2),
∴阴影的面积=扇形ODE的面积﹣△ODF的面积=(2π﹣)(cm2).
24.【分析】(1)将点A和点B代入解析式,求出a和b即可得到抛物线表达式;
(2)过点P作PD∥y轴交BC于点D,设点P(x,)(0<x<4),D(x,x﹣4),==﹣x2+4x=﹣(x2﹣4x+4﹣4)=﹣(x﹣2)2+4,得出当x=2,即点P(2,﹣4)时,△PBC的面积取得最大值,最大值为4;
(3)B(4,0),P(2,﹣4),N(x,x﹣4),Q(m,n),分①以BN、PQ为对角线,BP=PN,②以BQ、NP为对角线,BP=BN,两种情况进行讨论.
【解答】解:(1)∵y=ax2+bx﹣4交x轴于点A(﹣2,0)和点B(4,0),
∴,
∴,
∴;
(2)当x=0时,y=﹣4,
∴C(0,﹣4),
过点P作PD∥y轴交BC于点D,
∵B(4,0),C(0,﹣4),
∴BC:y=x﹣4,
设点P(x,)(0<x<4),
∴D(x,x﹣4),
∴PD=(x﹣4)﹣()=,
∵
=
=﹣x2+4x
=﹣(x2﹣4x+4﹣4)
=﹣(x﹣2)2+4,
∴当x=2,即点P(2,﹣4)时,△PBC的面积取得最大值,最大值为4;
(3)B(4,0),P(2,﹣4),N(x,x﹣4),Q(m,n),
①以BN、PQ为对角线,BP=PN,
∴,
∴或(舍),
∴Q(0,﹣2);
②以BQ、NP为对角线,BP=BN,
∴,
∴或,
∴Q(,)或Q(,);
综上所述:Q(0,﹣2)或Q(,)或Q(,).
浙江省2024年秋季九年级上册第一次月考数学检测卷
范围:第1-3章 满分:120分 时间:120分钟
题号 选择题 填空题 解答题
得分
一.选择题(共10小题,满分30分,每小题3分)
1.二次函数y=x2+2x+1的顶点坐标为( )
A.(﹣1,0) B.(1,0) C.(0,﹣1) D.(0,1)
2.为了丰富校园生活,培养学生特长,学校开展了特色课程.小明从感兴趣的“花样跳绳”“天文地理”“艺术插花”“象棋博交”4门课程中随机选择一门学习.小明选中“天文地理”这一门课程的概率为( )
A. B. C. D.
3.如图,将△AOB绕点O按逆时针方向旋转50°后得到△COD,若∠AOB=20°,则∠AOD的度数是( )
A.20° B.30° C.40° D.50°
4.如图,AB是圆O的直径,CD是圆O的弦,∠ABD=69°,则∠C等于( )
A.29° B.21° C.31° D.62°
5.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.36左右,则布袋中黄球估计有( )
A.18个 B.22个 C.28个 D.32个
6.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=﹣ax+b的图象大致是( )
A. B.
C. D.
7.如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是( )
A.50° B.80° C.90° D.100°
8.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x cm,它的面积为y cm2,则y与x之间的函数关系式为( )
A.y=﹣x2+50x B.y=x2﹣50x
C.y=﹣x2+25x D.y=﹣2x2+25x
9.已知二次函数y=ax2﹣2ax+1(a为常数,且a<0)的图象上有三点A(﹣2,y1),B(1,y2),C(3,y3),则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y1<y3 D.y2<y3<y1
10.如图,△BCD内接于⊙O,点B是的中点,CD是⊙O的直径.若∠ABC=30°,AC=4,则BC的长为( )
A.5 B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.写出一个开口向下,顶点为(1,2)的二次函数 .
12.已知⊙O的半径为5,点P在⊙O上,则OP的长为 .
13.某商场为吸引顾客设计了如图所示的自由转盘,当指针指向阴影部分(含边界)时,该顾客可获奖品一份,那么该顾客获奖的概率为 .
14.将抛物线y=﹣2(x+2)2向右平移3个单位长度,再向下平移4个单位长度得到的抛物线的函数解析式为 .
15.如图,已知⊙O的内接正六边形ABCDEF的边长为4,H为边AF的中点,则图中阴影部分的面积是 .
16.已知二次函数y=ax2+bx+c的图象经过(1,0),(﹣2,t)两点,其中t<0,对称轴为x=﹣1.下列四个结论:①bc<0;②c=t;③点A(s,y1)、B(s+1,y2)在抛物线上,当s<﹣1时,y1>y2;④已知关于x的方程ax2+bx+c﹣m=0(m>0)有两个根,其中一个根是3,若关于x的方程ax2+bx+c﹣n=0(0<n<m)有整数根,则其根为﹣4和2;其中正确的结论是 (填写序号).
三.解答题(共8小题,满分72分)
17.(7分)如图,已知⊙O内接ABC,AD为⊙O直径,AE⊥BC于E点,连接BD.求证:∠BAD=∠CAE.
18.(7分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕O顺时针旋转90°后的△A2B2C2并写出点C2的坐标.
19.(8分)如图,一座石桥的主桥拱是圆弧形,某时刻测得水面AB的宽度为8m,拱高CD(的中点到水面的距离)为2m.
(1)求所在圆的半径;
(2)若水面下降1m,求此时水面的宽度(保留根号).
20.(8分)从背面相同的同一副扑克牌中取出9张红桃,10张黑桃,11张方块.
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉9张红桃和m(m>6)张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,再从桌面上随机抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
21.(8分)【探究】如图,已知抛物线y=﹣x2+4.
(1)在坐标系中画出此抛物线y的大致图象(不要求列表);
(2)该抛物线y=﹣x2+4可由抛物线y=﹣x2向 平移 个单位得到;
(3)当﹣1≤x≤3时,函数值y取值范围是 .
【应用】已知二次函数y=﹣(x﹣h)2(h是常数),且自变量取值范围是2≤x≤5.
(1)当h=3时,求函数的最大值;
(2)若函数的最大值为﹣1,求h的值.
22.(10分)排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生在O处将球垫偏,之后又在A、B两处先后垫球,球沿抛物线C1→C2→C3运动(假设抛物线C1、C2、C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点,点B的横坐标为,抛物线C1表达式为y=ax2﹣2ax和抛物线C3表达式为y=2ax2+bx(a≠0).
(1)求抛物线C1的函数表达式;
(2)第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;
(3)为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处B离地面的高度至少为多少米?
23.(12分)如图,在△ABC中,∠C=90°,点M在圆O上,AC交圆O于点M,BC与圆O交于点D,DM=DE,DE⊥AD交AB于点E,AE为⊙O的直径,DF⊥AB.
(1)求证:∠CAD=∠DAB;
(2)若DM平分∠ADC,求∠CAD的度数;
(3)若AD=BD=6cm,求图中阴影部分的面积.
24.(12分)如图,抛物线y=ax2+bx﹣4交x轴于点A(﹣2,0)和点B(4,0),交y轴于点C.
(1)求抛物线的表达式;
(2)若点P是直线BC下方抛物线上一动点,连接PC,PB,当△PBC的面积最大时,求点P的坐标及面积的最大值;
(3)在(2)的条件下,若点N是直线BC上的动点,在平面内的是否存在点Q,使得以PB为边、以P、B、N、Q和顶点的四边形是菱形?若存在,请求出符合条件的所有Q点的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【分析】利用函数顶点式解答即可.
【解答】解:y=x2+2x+1=(x+1)2,
二次函数顶点坐标为(﹣1,0),
故选:A.
2.【分析】直接根据概率公式解答即可.
【解答】解:∵小明从感兴趣的“花样跳绳”“天文地理”“艺术插花”“象棋博交”4门课程中随机选择一门学习,
∴小明选中“天文地理”这一门课程的概率为.
故选:B.
3.【分析】首先根据旋转变换的性质求出∠BOD=50°,结合∠AOB=20°,即可解决问题.
【解答】解:由题意及旋转变换的性质得:∠BOD=50°,
∵∠AOB=20°,
∴∠AOD=50°﹣20°=30°,
故选:B.
4.【分析】首先根据同弧所对的圆周角相等求得角A的度数,然后再求得∠ABD的度数即可.
【解答】解:∵AB是直径,
∴∠ADB=90°,
∵∠ABD=69°,
∴∠A=21°,
∴∠C=21°,
故选:B.
5.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
【解答】解:设袋中有黄球x个,由题意得=0.36,
解得x=18,
∴黄球可能有18个.
故选:A.
6.【分析】可先根据二次函数的图象判断a、b的符号,再判断一次函数图象与实际是否相符,判断正误.
【解答】解:由二次函数图象,得出a<0,b<0,
A、一次函数图象,得a<0,b>0,故A错误;
B、一次函数图象,得a>0,b>0,故B错误;
C、一次函数图象,得a<0,b<0,故C正确;
D、一次函数图象,得a>0,b<0,故D错误;
故选:C.
7.【分析】根据圆内接四边形的性质得出∠A+∠C=180°,再代入求出答案即可.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠C=100°,
∴∠A=80°,
故选:B.
8.【分析】要求长方形的面积,需求出长方形相邻两边的长度,根据长方形的周长公式可计算出长方形另一边的长为(25﹣x)cm;接下来,根据长方形的面积公式即可得到y与x的函数关系式.
【解答】解:设这个长方形的一边长为x cm,周长是50cm,
∴另一边长是(25﹣x)cm,
∴y与x的函数关系式为:y=x(25﹣x)=﹣x2+25x.
选项A、B、D都不正确,选项C正确.
故选:C.
9.【分析】先确定对称轴,根据把点A的对称点确定,转化为对称轴同侧的点,根据抛物线开口向下,对称轴的右侧y随x的增大而减小即可得到解答.
【解答】解:∵二次函数y=ax2﹣2ax+1(a为常数,且a<0)的图象上有三点A(﹣2,y1),B(1,y2),C(3,y3),
∴对称轴.
设点A的对称点为(x0,y1),
所以.
解得x0=4,
∴点A的对称点为(4,y1).
∵a<0,
∴抛物线开口向下.
∴对称轴的右侧y随x的增大而增减小.
∵4>3>1,
所以y1<y3<y2.
故选:B.
10.【分析】连接OA,先根据圆周角定理可得∠AOC=2∠ABC=60°,从而可得△AOC是等边三角形,根据等边三角形的性质可得AC=OC=4,从而可得DC=2OC=8,然后根据直径所对的圆周角是直角可得∠CBD=90°,再根据已知可得=,从而可得CB=BD,最后根据等腰直角三角形的性质进行计算即可解答.
【解答】解:连接OA,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OC=4,
∴DC=2OC=8,
∵CD是⊙O的直径,
∴∠CBD=90°,
∵点B是的中点,
∴=,
∴CB=BD,
∴BC==4,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.【分析】因为顶点为(1,2),所以设y=a(x﹣1)2+2,因为开口向下,所以a<0,据此即可作答.
【解答】解:∵顶点为(1,2),
∴设二次函数的解析式y=a(x﹣1)2+2,
∵开口向下,
∴a=﹣1<0,
∴y=﹣(x﹣1)2+2,
故答案为:y=﹣(x﹣1)2+2(答案不唯一).
12.【分析】根据d=r时点在圆上解决问题即可.
【解答】解:∵⊙O的半径为5,点P在⊙O上,
∴OP=r=5.
故答案为:5.
13.【分析】先求出45°在整个转盘中所占面积的比值,根据此比值即可解答.
【解答】解:阴影部分占45°,
则其占整个圆面积的=,
即该顾客获奖的概率为.
故答案为:.
14.【分析】由平移的规律即可求得答案.
【解答】解:将抛物线y=﹣2(x+2)2向右平移3个单位,则函数解析式变为y=﹣2(x+2﹣3)2=﹣2(x﹣1)2,向下平移4个单位长度得到的抛物线的函数解析式为y=﹣2(x﹣1)2﹣4.
故答案为:y=﹣2(x﹣1)2﹣4.
15.【分析】根据题意先计算出S△CDH的面积,再计算扇形COD面积及S△COD面积,即可得到本题答案.
【解答】解:过点H作HE⊥CD交CD于点Q,连接OC,OD,
∵⊙O的内接正六边形ABCDEF的边长为4,H为边AF的中点,
∴∠COD=60°,∠QCO=60°,CO=OD=4,Q为边CD的中点,
∴CQ=DQ=2,
∴OQ=2,
∴QH=4,
∴,
∴扇形COD面积:,
∵,
∴阴影部分的面积:,
故答案为:.
16.【分析】利用二次函数的图象及性质,系数间的关系和一元二次方程的关系即可求解.
【解答】解:∵抛物线过(1,0),对称轴为x=﹣1,
∴图象必过(﹣3,0),
又∵过点(﹣2,t)(t<0),
∴开口向上,与y轴交于负半轴,
∴a>0,b>0,c<0,故①对;
∵(0,c)与(﹣2,t)到对称轴等距,
∴c=t,故②对;
∵s<﹣1,无法判断点A(s,y1)、B(s+1,y2)与对称轴是同侧还是异侧,
也就无法判断点A、B与对称轴x=﹣1的距离的大小,故无法比较y1与y2的大小,故③错;
∵方程ax2+bx+c=0的两根分别为1和﹣3,
又x的方程ax2+bx+c﹣m=0(m>0)有两个根,其中一个根是3,而抛物线的对称轴为x=﹣1,由对称性得另一个根为﹣5,
观察图象,得关于x的方程ax2+bx+c﹣n=0(0<n<m)整数根为﹣4和2,故④对,
故答案为:①②④.
三.解答题(共8小题,满分72分)
17.【分析】由圆周角定理,推出∠ABD=90°,∠D=∠C,由垂直的定义得到∠AEC=90°,由三角形内角和定理推出∠BAD=∠CAE.
【解答】证明:∵AD是圆的直径,
∴∠ABD=90°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠ABD=∠AEC,
∵∠D=∠C,
∴∠BAD=∠CAE.
18.【分析】(1)分别确定A,B,C关于原点的对称点A1,B1,C1,再顺次连接A1,B1,C1,可得答案;
(2)分别确定A,B,C绕原点O顺时针旋转90°后的对应点A2,B2,C2,再顺次连接A2,B2,C2,再根据C2的位置可得答案.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;C2(4,﹣3).
19.【分析】(1)根据垂径定理得到OC⊥AB,AC=BC,结合勾股定理求解即可得到答案;
(2)根据(1)即可得到OG=5﹣1﹣2=2m,OF=5m,结合勾股定理求解即可得到答案;
【解答】(1)解:如图,设所在圆的圆心为O,连接OA,OC,
∵D是的中点,CD⊥AB,即OD为圆的半径,
∴,
设OA=OD=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,OA2=OC2+AC2,
即r2=(r﹣2)2+42,解得r=5,故所在圆的半径为5m;
(2)解:如图,连接OF,设OD与EF交于点G,则∠OGF=90°,
在Rt△OGF中,OG=5﹣1﹣2=2(m),OF=5m,
∴,
∴,
故此时水面的宽度为.
20.【分析】(1)由概率公式计算即可;
(2)①事件“再抽出的这张牌是方块”为必然事件,则剩下的牌只有方块,即可得出答案;
②事件“再抽出的这张牌是方块”为随机事件,则剩下的牌有黑桃和方块,再由m>6和概率公式即可得出答案.
【解答】解:(1)从中随机抽出一张是红桃的概率是=;
(2)①∵事件“再抽出的这张牌是方块”为必然事件,则剩下的牌只有方块,
∴当m为10时,事件“再抽出的这张牌是方块”为必然事件,
②∵事件“再抽出的这张牌是方块”为随机事件,
∴剩下的牌有黑桃和方块,
∵m>6,
∴当m为9、8、7时,事件“再抽出的这张牌是方块”为随机事件事件,
这个事件的概率的最小值为:=.
21.【分析】探究(1)依据题意,函数为y=﹣x2+4,则抛物线开口向下,对称轴是y轴,顶点为(0,4),进而可以作图;
(2)依据题意,根据平移规律“上加下减,左加右减”,进而可以判断得解;
(3)依据题意,由抛物线为y=﹣x2+4,故当x=0时,y取最大值为4,结合当x=﹣1时,y=3;当x=3时,y=﹣5,进而可以判断得解;
应用(1)依据题意,由h=3,可得二次函数为:y=﹣(x﹣3)2,故当x=3时,函数有最大值为0,结合2≤x≤5,从而可以判断得解;
(2)依据题意,二次函数y=﹣(x﹣h)2(h为常数),当自变量x满足2≤x≤5时,其对应函数y的最大值为﹣1,进而分5<h、h<2和2<h<5分别进行计算分析可以得解.
【解答】解:探究(1)由题意,函数为y=﹣x2+4,
∴抛物线开口向下,对称轴是y轴,顶点为(0,4).
作图如下.
(2)由题意,∵抛物线为y=﹣x2+4,
又根据平移规律“上加下减,左加右减”,
∴抛物线为y=﹣x2+4可由y=﹣x2向上平移4个单位得到.
故答案为:4.
(3)由题意,∵抛物线为y=﹣x2+4,
∴当x=0时,y取最大值为4,
又当x=﹣1时,y=3;当x=3时,y=﹣5,
∴当﹣1≤x≤3时,﹣5≤y≤4.
故答案为:﹣5≤y≤4.
应用(1)由题意,∵h=3,
∴二次函数为:y=﹣(x﹣3)2.
∴当x=3时,函数有最大值为0.
∵2≤x≤5,
∴当x=3时,函数有最大值为0,符合题意.
(2)∵二次函数y=﹣(x﹣h)2(h为常数),当自变量x满足2≤x≤5时,其对应函数y的最大值为﹣1,
∴若5<h,则当x=5时,y最大,即﹣(5﹣h)2=﹣1,得h1=4(舍去),h2=6;
若h<2,则当x=2时,y最大,即﹣(2﹣h)2=﹣1,得h3=1,h4=3(舍去);
若2<h<5,则最大值为0,与题意不符;
由上可得,h的值是6或1.
22.【分析】(1)直接利用待定系数法,即可求出抛物线C1的函数表达式;
(2)将抛物线C1表达式化为顶点式,得到顶点坐标,求出实际最大高度,即可得到答案;
(3)由(1)可知,,得到抛物线C3表达式为y=﹣x2+bx,进而得到对称轴为直线,顶点坐标为,根据最大高度的要求和对称轴,求出b≤﹣2,再根据点B的横坐标为,得到,求出yB的最小值即可得到答案.
【解答】解:(1)∵抛物线C1表达式为y=ax2﹣2ax,且经过点,
∴,
解得:,
∴抛物线C1的函数表达式为:;
(2)最大高度未达到要求,理由如下:
由(1)得,抛物线C1的函数表达式为,
∵,
∴抛物线C1的顶点坐标为,
∵O处离地面的距离为1米,
∴球在运动中离地面的最大高度为,
∴最大高度未达到要求;
(3)解:由(1)可知,,
∵抛物线C3表达式为y=﹣x2+bx,
∴对称轴为直线,顶点坐标为,
∵球在运动中离地面的最大高度达到要求,
∴,
∴b≥2或b≤﹣2,
∵对称轴在x轴负半轴,
∴b<0,
∴b≤﹣2,
∵点B的横坐标为,
∴,
∴当b=﹣2时,yB有最小值,最小值为,
∴点B离地面的高度至少为(米).
23.【分析】(1)根据圆周角定理即可得出答案;
(2)由角平分线定义得到∠CDM=∠ADM,由等腰三角形的性质,余角的性质推出∠CDM=∠CAD,由直角三角形的性质即可求出∠CAD的度数;
(3)由等腰三角形的性质,直角三角形的性质求出∠B的度数,得到∠DOE=60°,由直角三角形的性质求出DF,OF,OD的长,求出扇形ODE的面积,△ODF的面积,即可求出阴影的面积.
【解答】(1)证明:∵DM=DE,
∴=,
∴∠CAD=∠DAB;
(2)解:连接OM,OD,作OH⊥MD于H,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠CAD=∠DAB,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90,
∴AC⊥BC,
∴OD⊥BC,
∴∠MDC+∠MDO=90°,
∵OM=OD,OH⊥MD,
∴∠DOH=∠MOD,
∵∠CAD=∠MOD,
∴∠CAD=∠DOH,
∵∠DOH+∠MDO=90°,
∴∠DOH=∠CDM,
∴∠CAD=∠CDM,
∵DM平分∠ADC,
∴∠CDM=∠ADM,
∵∠CAD+∠ADM+∠CDM=90°,
∴∠CAD=30°;
(3)解:∵DA=DB,
∴∠DAB=∠B,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠DOB=∠DAB+∠ADO=2∠B,
∵∠DOB+∠B=90°,
∴∠B=∠DAB=30°,
∴∠BOD=60°,
∵AD=6cm,
∴DF=AD=3cm,
∴OF=FD=cm,
∴OD=2OF=2cm,
∴扇形ODE的面积==2π(cm2),△ODF的面积=OF DF=×3×=(cm2),
∴阴影的面积=扇形ODE的面积﹣△ODF的面积=(2π﹣)(cm2).
24.【分析】(1)将点A和点B代入解析式,求出a和b即可得到抛物线表达式;
(2)过点P作PD∥y轴交BC于点D,设点P(x,)(0<x<4),D(x,x﹣4),==﹣x2+4x=﹣(x2﹣4x+4﹣4)=﹣(x﹣2)2+4,得出当x=2,即点P(2,﹣4)时,△PBC的面积取得最大值,最大值为4;
(3)B(4,0),P(2,﹣4),N(x,x﹣4),Q(m,n),分①以BN、PQ为对角线,BP=PN,②以BQ、NP为对角线,BP=BN,两种情况进行讨论.
【解答】解:(1)∵y=ax2+bx﹣4交x轴于点A(﹣2,0)和点B(4,0),
∴,
∴,
∴;
(2)当x=0时,y=﹣4,
∴C(0,﹣4),
过点P作PD∥y轴交BC于点D,
∵B(4,0),C(0,﹣4),
∴BC:y=x﹣4,
设点P(x,)(0<x<4),
∴D(x,x﹣4),
∴PD=(x﹣4)﹣()=,
∵
=
=﹣x2+4x
=﹣(x2﹣4x+4﹣4)
=﹣(x﹣2)2+4,
∴当x=2,即点P(2,﹣4)时,△PBC的面积取得最大值,最大值为4;
(3)B(4,0),P(2,﹣4),N(x,x﹣4),Q(m,n),
①以BN、PQ为对角线,BP=PN,
∴,
∴或(舍),
∴Q(0,﹣2);
②以BQ、NP为对角线,BP=BN,
∴,
∴或,
∴Q(,)或Q(,);
综上所述:Q(0,﹣2)或Q(,)或Q(,).
同课章节目录
