2024年山东省淄博市中考数学试题(PDF版无答案)
文档属性
| 名称 | 2024年山东省淄博市中考数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 22:08:44 | ||
图片预览



文档简介
2024年淄博市初中学业水平考试数学试题
一、选择题(本大题共 10小题,每题 4分,共 40分)
1.下列运算结果是正数的是 ( )
(A) 3-1 (B) - 32 (C) - -3 (D) - 3
2.下列图案中,既是轴对称图形又是中心对称图形的是 ( )
(A) (B) (C) (D)
3.我国大力发展新质生产力,推动了新能源汽车产业的快速发展。据中国汽车工业协会发布的消
息显示。 2024年 1至 3月,我国新能源汽车完成出口 30.7万辆。将 30.7万用科学记数法表示为
3.07× 10n.则 n的值是 ( )
(A) 4 (B) 5 (C) 6 (D) 7
4.如图,已知 AD BC,BD平分∠ABC。若∠A= 110°,则∠D的度数是 ( )
A D
B C
第4题图
(A) 40° (B) 36° (C) 35° (D) 30°
5.数学兴趣小组成员小刚对自己的学习质量进行了测试。右图是他最近五次测试成绩(满分为
100分)的折线统计图,那么其平均数和方差分别是 ( )
成绩/分
100 100 9996
92 93
90
80
0 1 2 3 4 5 次数
(第5题图)
(A) 95分, 10 (B) 96分, 10 (C) 95分,10 (D) 96分,10
6.如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长 BC为 35m.又在点C处测
得该楼的顶端 A的仰角是 29°。则用科学计算器计算教学楼高度的按键顺序正确的是 ( )
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
A
C B
(第6题图)
(A) 3 5 × tan 2 9 = (B) 3 5 ÷ tan 2 9 =
(C) 3 5 × sin 2 9 = (D) 3 5 × cos 2 9 =
7.如图,其大意为:已知矩形门的高比宽多 6尺 8寸,门的对角线长 1丈,那么门的高和宽各是多
少? 1丈=10尺,1尺=10寸 若设门的高和宽分别是 x尺和 y尺。则下面所列方程组正确的是
( )
今有户高多于广六
尺八寸。两隅相去适一
丈。问户高、广各几何?
《九章算术》
(第7题图)
(A) x=y-6.8 x=y-6.8 x=y+6.8 x=y+6.8 x2+102=y2 (B) x2+y2=102 (C) x2+102=y2 (D) x2+y2=102
8.如图所示,在矩形 ABCD中,BC = 2AB,点 M ,N分别在边 BC ,AD上。连接 MN,将四边形
CMND沿MN翻折,点C,D分别落在点 A,E处。则 tan∠AMN的值是 ( )
E
A N D
B M C
(第8题图)
(A) 2 (B) 2 (C) 3 (D) 5
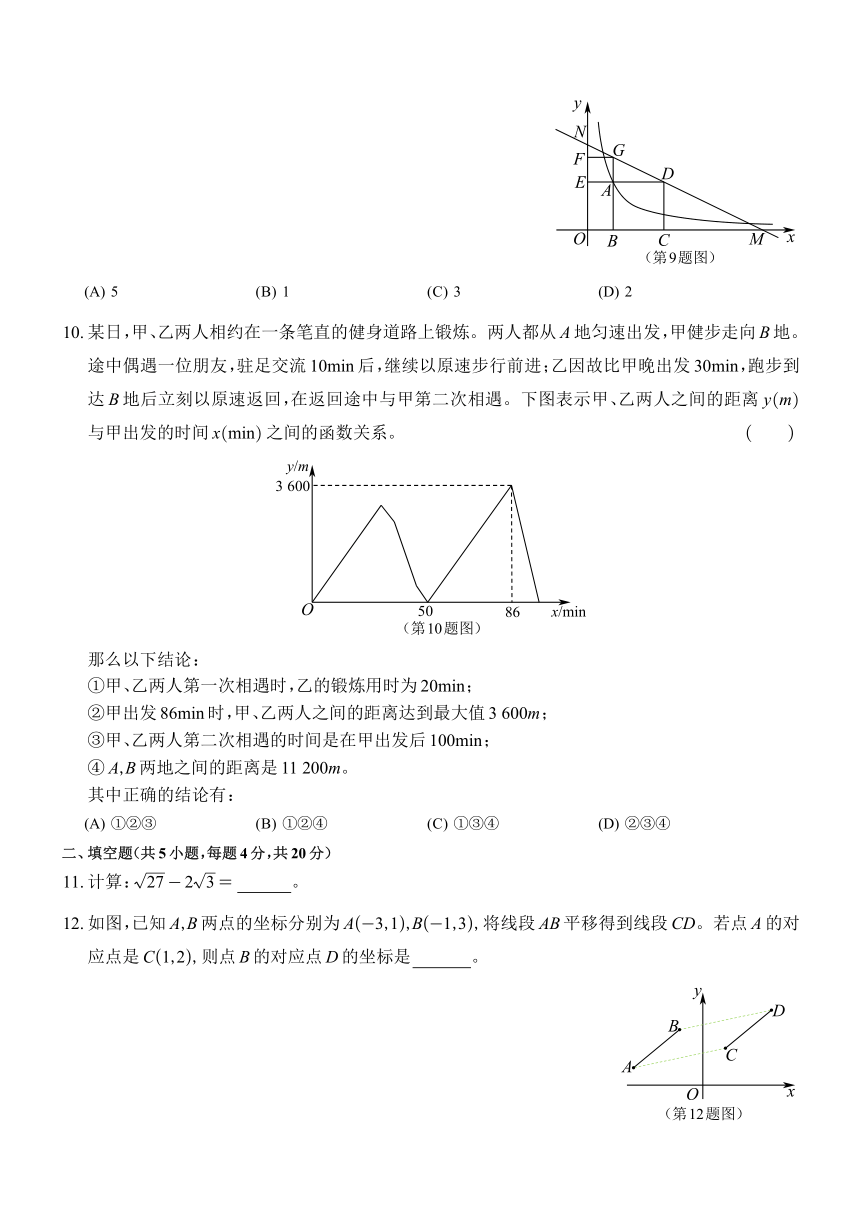
9.如图所示,正方形 ABCD与 AEFG 其中边BC,EF分别在x,y轴的正半轴上 的公共顶点 A在反
y= k比例函数 x 的图象上,直线DG与 x,y轴分别相交于点M ,N。若这两个正方形的面积之和
15
是 2 ,且MD= 4GN .则 k的值是 ( )
{#{QQABaYS0Q4ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
y
N
F G
E DA
O B C M x
(第9题图)
(A) 5 (B) 1 (C) 3 (D) 2
10.某日,甲、乙两人相约在一条笔直的健身道路上锻炼。两人都从 A地匀速出发,甲健步走向 B地。
途中偶遇一位朋友,驻足交流 10min后,继续以原速步行前进;乙因故比甲晚出发 30min,跑步到
达 B地后立刻以原速返回,在返回途中与甲第二次相遇。下图表示甲、乙两人之间的距离 y m
与甲出发的时间 x min 之间的函数关系。 ( )
y/m
3 600
O 50 86 x/min
(第10题图)
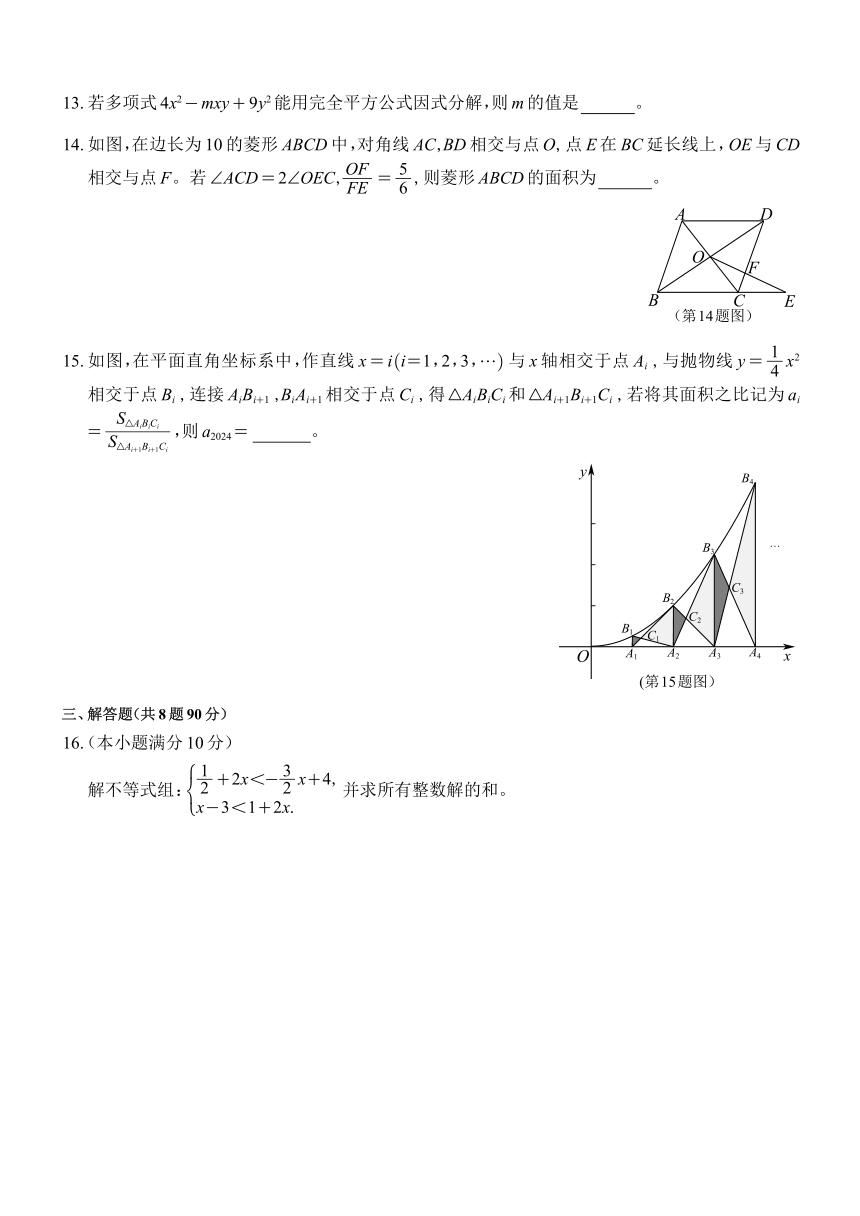
那么以下结论:
①甲、乙两人第一次相遇时,乙的锻炼用时为 20min;
②甲出发 86min时,甲、乙两人之间的距离达到最大值 3 600m;
③甲、乙两人第二次相遇的时间是在甲出发后 100min;
④ A,B两地之间的距离是 11 200m。
其中正确的结论有:
(A) ①②③ (B) ①②④ (C) ①③④ (D) ②③④
二、填空题(共 5小题,每题 4分,共 20分)
11.计算: 27- 2 3= 。
12.如图,已知 A,B两点的坐标分别为 A(-3,1),B(-1,3),将线段 AB平移得到线段CD。若点 A的对
应点是C(1,2),则点 B的对应点D的坐标是 。
y
D
B
C
A
O x
(第12题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
13.若多项式 4x2-mxy+ 9y2能用完全平方公式因式分解,则m的值是 。
14.如图,在边长为 10的菱形 ABCD中,对角线 AC,BD相交与点O,点 E在 BC延长线上,OE与CD
相交与点 F ∠ACD= 2∠OEC,OF。若 FE =
5
6 ,则菱形 ABCD的面积为 。
A D
O F
B C E
(第14题图)
15. 1如图,在平面直角坐标系中,作直线 x= i i=1,2,3, 与 x轴相交于点 Ai ,与抛物线 y= x24
相交于点 Bi ,连接 AiBi+1 ,BiAi+1相交于点Ci ,得△AiBiCi和△Ai+1Bi+1Ci ,若将其面积之比记为 ai
S
= △AiBiCiS ,则 a2024= 。△Ai+1Bi+1Ci
y B4
B3
C
B 32
C2
B1 C1
O A1 A2 A3 A4 x
(第15题图)
三、解答题(共 8题 90分)
16(. 本小题满分 10分)
1 +2x<- 3 x+4,
解不等式组: 2 2 并求所有整数解的和。x-3<1+2x.
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
17(. 本小题满分 10分)
如图,已知 AB=CD,点 E,F在线段 BD上,且 AF=CE。
请从① BF= DE;②∠BAF=∠DCE;③ AF= CF中.选择一个合适的选项作为已知条件,使得
△ABF≌△CDE。
你添加的条件是: (只填写一个序号)。
添加条件后,请证明 AE CF。
A B
F
E
D C
(第17题图)
18(. 本小题满分 10分)
a2-b2 1-a-b
化简分式:
a2- + 2 + a-b ,并求值(请从小宇和小丽的对话中确定 a,b的值)2ab b
a 3 b是大于1且是 的
小于 5的整数。
相反数。
小宇 小丽
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
19(. 本小题满分 10分)
希望中学做了如下表的调查报告(不完整):
调查目的 了解本校学生(:1)周家务劳动的时间(;2)最喜欢的劳动课程
调查方式 随机问卷调查
调查对象 部分七年级学生(该校所有学生周家务劳动时间都在 1~3.5h范围内)
(1)你的周家务劳动时间(单位:h)是
① 1~1.5② 1.5~2③ 2~2.5④ 2.5~3⑤ 3~3.5
调查内容
(2)你最喜欢的劳动课程是(必选且只选一门)
A.家政 B.烹饪 C.剪纸 D.园艺 E.陶艺
周家务劳动时间频数直方图 劳动课程条形统计图
人数(频数) 周家务劳动时间扇形统计图 人数
40 2635 2435 24
30 ⑤ ① 22
25 ② 20 20调查结果
20 20 20%④ 18 18
15 16
10 10 10 ③ 16
5 14
0 1 1.5 2 2.5 3 3.5 0时间 /h 家政烹饪 剪纸 园艺 陶艺 课程
结合调查信息,回答下列问题:
1 参与本次问卷调查的学生人数 名;在扇形统计图中,第④组所对应扇形的圆心角的度数为
度;
2 补全周家务劳动时间的频数直方图:
3 若该校七年级学生共有 800人,请估计最喜欢“烹饪”课程的学生人数;
4 小红和小颖分别从“家政”等五门最喜欢的劳动课程中任选一门学习,请用列表法或画树状图的方法,求两
人恰好选到同一门课程的概率。
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
20(. 本小满分 12分)
“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高。某市参加健身运动的人数
逐年增多,从 2021年的 32万人增加到 2023年的 50万人。
1 求该市参加健身运动人数的年均增长率;
2 为支持市民的健身运动,市政府决定从 A公司购买某种套装健身器材。该公司规定:若购买
不超过 100套,每套售价 1600元;若超过 100套,每增加 10套,售价每套可降低 40元。但最低售
价不得少于 1000元。已知市政府向该公司支付货款 24万元,求购买的这种健身器材的套数。
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
21(. 本小题满分 12分)
= + = k2如图,一次函数 y k1x 2的图象与反比例函数 y x 的图象相交于 A m,4 ,B两点,与 x,y轴
分别相交于点C,D.且 tan∠ACO= 2。
1 分别求这两个函数的表达式;
2 以点 D为圆心,线段 DB的长为半径作弧与 x轴正半轴相交于点 E,连接 AE,BE。求△ABE
的面积;
k
3 根据函数的图象直接写出关于 x的不等式 k1x+ 2> 2x 的解集。
y
A
D
C
O E x
B
(第21题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
22(. 本小题满分 13分)
在综合与实践活动课上,小明以“圆”为主题开展研究性学习。
【操作发现】
小明作出了⊙O的内接等腰三角形 ABC,AB= AC.并在 BC边上任取一点D(不与点 B,C重合),
连按 AD,然后将△ABD绕点 A逆时针旋转得到△ACE.如图①
小明发现:CE与⊙O的位置关系是 ,请说明理由:
【实践探究】
连接 DE,与 AC相交于点 F.如图②,小明又发现:当△ABC确定时,线段 CF的长存在最大值。
请求出当 AB= 3 10 .BC= 6时,CF长的最大值;
【问题解决】
在图②中,小明进一步发现:点 D分线段 BC所成的比 CD:DB与点 F分线段 DF所成的比 DF :
FE始终相等。请予以证明。
A A
O OE E
F
B D C B D C
图① 图②
(第22题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
23(. 本小题满分 13分)
如图,抛物线 y= ax2+ bx+ 3与 x轴相交于 A x1,0 ,B x2,0 两点(点 A在点 B的左侧),其中 x1,
x2是方程 x2- 2x- 3= 0的两个根,抛物线与 y轴相交于点C。
1 求该抛物线对应的函数表达式;
2 已知直线 l:y= 3x+ 9与 x,y轴分别相交于点D,E。
①设直线 BC与 l相交于点 F,问在第三象限内的抛物线上是否存在点 P,使得∠PBF=∠DFB?
若存在,求出点 P的坐标;若不存在,说明理由;
②过抛物线上一点M作直线 BC的平行线.与抛物线相交于另一点 N .设直线MB,NC相交于点
Q.连接QD,QE.求线段QD+QE的最小值。
y y
l l
E E
F F
C C
D B D B
A O x A O x
(第23题图) (备用图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
一、选择题(本大题共 10小题,每题 4分,共 40分)
1.下列运算结果是正数的是 ( )
(A) 3-1 (B) - 32 (C) - -3 (D) - 3
2.下列图案中,既是轴对称图形又是中心对称图形的是 ( )
(A) (B) (C) (D)
3.我国大力发展新质生产力,推动了新能源汽车产业的快速发展。据中国汽车工业协会发布的消
息显示。 2024年 1至 3月,我国新能源汽车完成出口 30.7万辆。将 30.7万用科学记数法表示为
3.07× 10n.则 n的值是 ( )
(A) 4 (B) 5 (C) 6 (D) 7
4.如图,已知 AD BC,BD平分∠ABC。若∠A= 110°,则∠D的度数是 ( )
A D
B C
第4题图
(A) 40° (B) 36° (C) 35° (D) 30°
5.数学兴趣小组成员小刚对自己的学习质量进行了测试。右图是他最近五次测试成绩(满分为
100分)的折线统计图,那么其平均数和方差分别是 ( )
成绩/分
100 100 9996
92 93
90
80
0 1 2 3 4 5 次数
(第5题图)
(A) 95分, 10 (B) 96分, 10 (C) 95分,10 (D) 96分,10
6.如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长 BC为 35m.又在点C处测
得该楼的顶端 A的仰角是 29°。则用科学计算器计算教学楼高度的按键顺序正确的是 ( )
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
A
C B
(第6题图)
(A) 3 5 × tan 2 9 = (B) 3 5 ÷ tan 2 9 =
(C) 3 5 × sin 2 9 = (D) 3 5 × cos 2 9 =
7.如图,其大意为:已知矩形门的高比宽多 6尺 8寸,门的对角线长 1丈,那么门的高和宽各是多
少? 1丈=10尺,1尺=10寸 若设门的高和宽分别是 x尺和 y尺。则下面所列方程组正确的是
( )
今有户高多于广六
尺八寸。两隅相去适一
丈。问户高、广各几何?
《九章算术》
(第7题图)
(A) x=y-6.8 x=y-6.8 x=y+6.8 x=y+6.8 x2+102=y2 (B) x2+y2=102 (C) x2+102=y2 (D) x2+y2=102
8.如图所示,在矩形 ABCD中,BC = 2AB,点 M ,N分别在边 BC ,AD上。连接 MN,将四边形
CMND沿MN翻折,点C,D分别落在点 A,E处。则 tan∠AMN的值是 ( )
E
A N D
B M C
(第8题图)
(A) 2 (B) 2 (C) 3 (D) 5
9.如图所示,正方形 ABCD与 AEFG 其中边BC,EF分别在x,y轴的正半轴上 的公共顶点 A在反
y= k比例函数 x 的图象上,直线DG与 x,y轴分别相交于点M ,N。若这两个正方形的面积之和
15
是 2 ,且MD= 4GN .则 k的值是 ( )
{#{QQABaYS0Q4ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
y
N
F G
E DA
O B C M x
(第9题图)
(A) 5 (B) 1 (C) 3 (D) 2
10.某日,甲、乙两人相约在一条笔直的健身道路上锻炼。两人都从 A地匀速出发,甲健步走向 B地。
途中偶遇一位朋友,驻足交流 10min后,继续以原速步行前进;乙因故比甲晚出发 30min,跑步到
达 B地后立刻以原速返回,在返回途中与甲第二次相遇。下图表示甲、乙两人之间的距离 y m
与甲出发的时间 x min 之间的函数关系。 ( )
y/m
3 600
O 50 86 x/min
(第10题图)
那么以下结论:
①甲、乙两人第一次相遇时,乙的锻炼用时为 20min;
②甲出发 86min时,甲、乙两人之间的距离达到最大值 3 600m;
③甲、乙两人第二次相遇的时间是在甲出发后 100min;
④ A,B两地之间的距离是 11 200m。
其中正确的结论有:
(A) ①②③ (B) ①②④ (C) ①③④ (D) ②③④
二、填空题(共 5小题,每题 4分,共 20分)
11.计算: 27- 2 3= 。
12.如图,已知 A,B两点的坐标分别为 A(-3,1),B(-1,3),将线段 AB平移得到线段CD。若点 A的对
应点是C(1,2),则点 B的对应点D的坐标是 。
y
D
B
C
A
O x
(第12题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
13.若多项式 4x2-mxy+ 9y2能用完全平方公式因式分解,则m的值是 。
14.如图,在边长为 10的菱形 ABCD中,对角线 AC,BD相交与点O,点 E在 BC延长线上,OE与CD
相交与点 F ∠ACD= 2∠OEC,OF。若 FE =
5
6 ,则菱形 ABCD的面积为 。
A D
O F
B C E
(第14题图)
15. 1如图,在平面直角坐标系中,作直线 x= i i=1,2,3, 与 x轴相交于点 Ai ,与抛物线 y= x24
相交于点 Bi ,连接 AiBi+1 ,BiAi+1相交于点Ci ,得△AiBiCi和△Ai+1Bi+1Ci ,若将其面积之比记为 ai
S
= △AiBiCiS ,则 a2024= 。△Ai+1Bi+1Ci
y B4
B3
C
B 32
C2
B1 C1
O A1 A2 A3 A4 x
(第15题图)
三、解答题(共 8题 90分)
16(. 本小题满分 10分)
1 +2x<- 3 x+4,
解不等式组: 2 2 并求所有整数解的和。x-3<1+2x.
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
17(. 本小题满分 10分)
如图,已知 AB=CD,点 E,F在线段 BD上,且 AF=CE。
请从① BF= DE;②∠BAF=∠DCE;③ AF= CF中.选择一个合适的选项作为已知条件,使得
△ABF≌△CDE。
你添加的条件是: (只填写一个序号)。
添加条件后,请证明 AE CF。
A B
F
E
D C
(第17题图)
18(. 本小题满分 10分)
a2-b2 1-a-b
化简分式:
a2- + 2 + a-b ,并求值(请从小宇和小丽的对话中确定 a,b的值)2ab b
a 3 b是大于1且是 的
小于 5的整数。
相反数。
小宇 小丽
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
19(. 本小题满分 10分)
希望中学做了如下表的调查报告(不完整):
调查目的 了解本校学生(:1)周家务劳动的时间(;2)最喜欢的劳动课程
调查方式 随机问卷调查
调查对象 部分七年级学生(该校所有学生周家务劳动时间都在 1~3.5h范围内)
(1)你的周家务劳动时间(单位:h)是
① 1~1.5② 1.5~2③ 2~2.5④ 2.5~3⑤ 3~3.5
调查内容
(2)你最喜欢的劳动课程是(必选且只选一门)
A.家政 B.烹饪 C.剪纸 D.园艺 E.陶艺
周家务劳动时间频数直方图 劳动课程条形统计图
人数(频数) 周家务劳动时间扇形统计图 人数
40 2635 2435 24
30 ⑤ ① 22
25 ② 20 20调查结果
20 20 20%④ 18 18
15 16
10 10 10 ③ 16
5 14
0 1 1.5 2 2.5 3 3.5 0时间 /h 家政烹饪 剪纸 园艺 陶艺 课程
结合调查信息,回答下列问题:
1 参与本次问卷调查的学生人数 名;在扇形统计图中,第④组所对应扇形的圆心角的度数为
度;
2 补全周家务劳动时间的频数直方图:
3 若该校七年级学生共有 800人,请估计最喜欢“烹饪”课程的学生人数;
4 小红和小颖分别从“家政”等五门最喜欢的劳动课程中任选一门学习,请用列表法或画树状图的方法,求两
人恰好选到同一门课程的概率。
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
20(. 本小满分 12分)
“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高。某市参加健身运动的人数
逐年增多,从 2021年的 32万人增加到 2023年的 50万人。
1 求该市参加健身运动人数的年均增长率;
2 为支持市民的健身运动,市政府决定从 A公司购买某种套装健身器材。该公司规定:若购买
不超过 100套,每套售价 1600元;若超过 100套,每增加 10套,售价每套可降低 40元。但最低售
价不得少于 1000元。已知市政府向该公司支付货款 24万元,求购买的这种健身器材的套数。
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
21(. 本小题满分 12分)
= + = k2如图,一次函数 y k1x 2的图象与反比例函数 y x 的图象相交于 A m,4 ,B两点,与 x,y轴
分别相交于点C,D.且 tan∠ACO= 2。
1 分别求这两个函数的表达式;
2 以点 D为圆心,线段 DB的长为半径作弧与 x轴正半轴相交于点 E,连接 AE,BE。求△ABE
的面积;
k
3 根据函数的图象直接写出关于 x的不等式 k1x+ 2> 2x 的解集。
y
A
D
C
O E x
B
(第21题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
22(. 本小题满分 13分)
在综合与实践活动课上,小明以“圆”为主题开展研究性学习。
【操作发现】
小明作出了⊙O的内接等腰三角形 ABC,AB= AC.并在 BC边上任取一点D(不与点 B,C重合),
连按 AD,然后将△ABD绕点 A逆时针旋转得到△ACE.如图①
小明发现:CE与⊙O的位置关系是 ,请说明理由:
【实践探究】
连接 DE,与 AC相交于点 F.如图②,小明又发现:当△ABC确定时,线段 CF的长存在最大值。
请求出当 AB= 3 10 .BC= 6时,CF长的最大值;
【问题解决】
在图②中,小明进一步发现:点 D分线段 BC所成的比 CD:DB与点 F分线段 DF所成的比 DF :
FE始终相等。请予以证明。
A A
O OE E
F
B D C B D C
图① 图②
(第22题图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
23(. 本小题满分 13分)
如图,抛物线 y= ax2+ bx+ 3与 x轴相交于 A x1,0 ,B x2,0 两点(点 A在点 B的左侧),其中 x1,
x2是方程 x2- 2x- 3= 0的两个根,抛物线与 y轴相交于点C。
1 求该抛物线对应的函数表达式;
2 已知直线 l:y= 3x+ 9与 x,y轴分别相交于点D,E。
①设直线 BC与 l相交于点 F,问在第三象限内的抛物线上是否存在点 P,使得∠PBF=∠DFB?
若存在,求出点 P的坐标;若不存在,说明理由;
②过抛物线上一点M作直线 BC的平行线.与抛物线相交于另一点 N .设直线MB,NC相交于点
Q.连接QD,QE.求线段QD+QE的最小值。
y y
l l
E E
F F
C C
D B D B
A O x A O x
(第23题图) (备用图)
{#{QQABaYSQ04ogggCwggANIBSAACBZg5CKAw0k0uKCCAAsMQQsIkMAjELUCgCMYAgORCAAJKAAQMLAAAJBNgIBINAA=B}#A}A=}#}
同课章节目录
