第十一章 三角形综合复习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十一章 三角形综合复习(含答案) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 268.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 18:44:03 | ||
图片预览


文档简介
十一章 三角形
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题10小题,每小题3分,共30分)
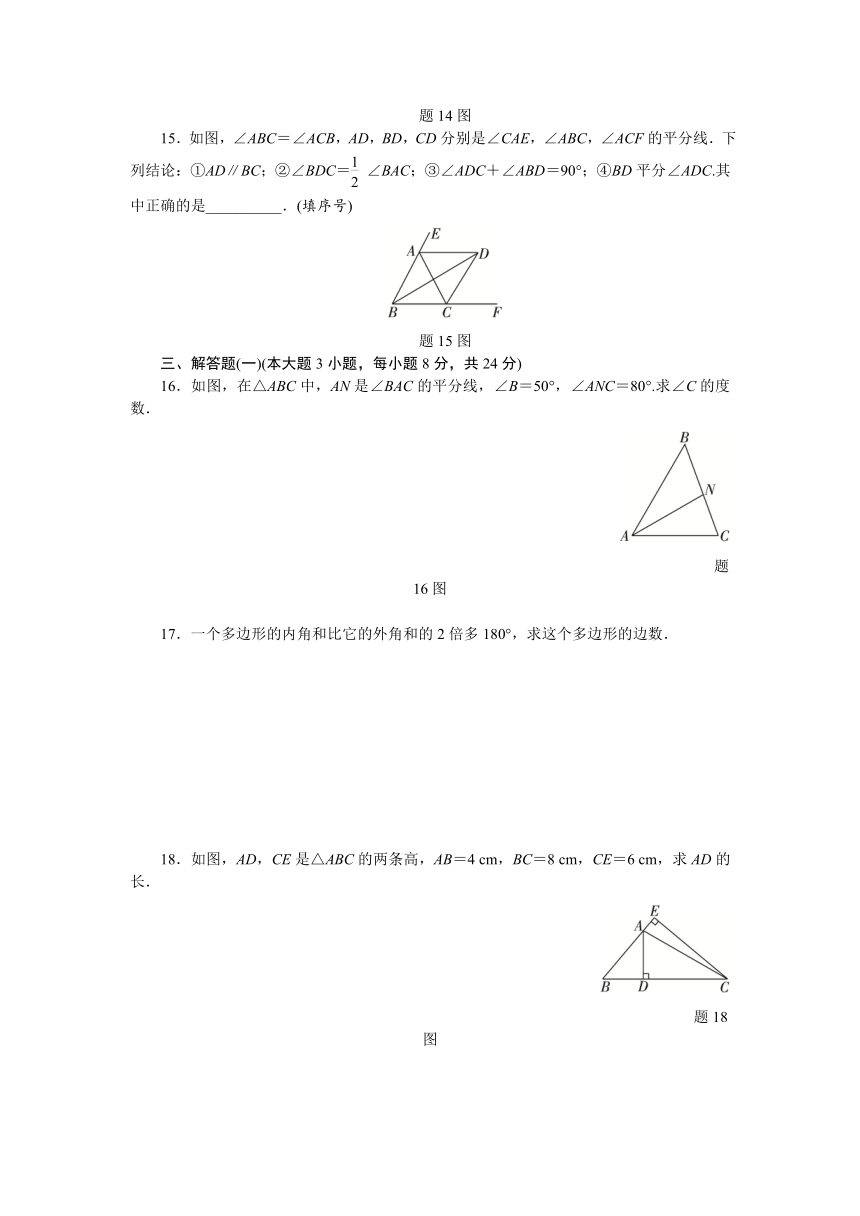
1.下列长度的三条线段,能组成三角形的是( )
A.2,2,4 B.4,5,8 C.3,6,9 D.5,5,11
2.安装空调时,一般会采用如图所示的方法固定,这样做的数学依据是( )
题2图
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,在△ABC中,边AC上的高是( )
题3图
A.线段AE B.线段CD C.线段AF D.线段BF
4.一个多边形的内角和为1 260°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
5.在△ABC中,若∠A∶∠B∶∠C=2∶3∶5,则该三角形的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
6.如图,已知Rt△ABC和Rt△DEF,∠D=∠ACB=90°,∠A=30°,∠F=45°,A,E,B,D四点在一条直线上,点C在EF上,则∠ECB的度数为( )
题6图
A.70° B.75° C.80° D.85°
7.如图,已知AD是△ABC的中线,CE是△ACD的中线,S△ACE=4,则S△ABC=( )
题7图
A.14 B.15 C.16 D.17
8.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=32°,∠CAD=24°,则∠B=( )
题8图
A.45° B.50° C.55° D.60°
9.(2023深圳)如图为商场某品牌椅子及其侧面示意图,∠DEF=120°,DE与地面平行,∠ABD=50°,则∠ACB=( )
题9图
A.70° B.65° C.60° D.50°
10.科技馆为某机器人编制了一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
题10图
A.6米 B.8米 C.10米 D.12米
二、填空题(本大题5小题,每小题3分,共15分)
11.已知三角形的三边长分别为5,x,8,则x的取值范围是__________.
12.在△ABC中,∠B=70°,∠C=25°,则∠A=__________.
13.如图,已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4 cm.若AB=16 cm,则AC=__________cm.
题13图
14.如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为__________.
题14图
15.如图,∠ABC=∠ACB,AD,BD,CD分别是∠CAE,∠ABC,∠ACF的平分线.下列结论:①AD∥BC;②∠BDC=∠BAC;③∠ADC+∠ABD=90°;④BD平分∠ADC.其中正确的是__________.(填序号)
题15图
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.如图,在△ABC中,AN是∠BAC的平分线,∠B=50°,∠ANC=80°.求∠C的度数.
题16图
17.一个多边形的内角和比它的外角和的2倍多180°,求这个多边形的边数.
18.如图,AD,CE是△ABC的两条高,AB=4 cm,BC=8 cm,CE=6 cm,求AD的长.
题18图
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=72°,求∠1和∠ADB的度数.
题19图
20.如图,已知B村在A村的南偏西50°方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A,B两个村庄的视角∠ACB的度数.
题20图
21.一个等腰三角形的周长为25 cm.
(1)若腰长是底边长的2倍,求各边的长;
(2)若其中一边的长为6 cm,求另两边的长.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE,CD相交于点F.
(1)若∠DCB=40°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
题22图
23.综合与实践
学习三角形内角和定理后,我们知道,任何一个三角形的三个内角之和都等于180°.请利用三角形内角和定理,解决以下问题:
【问题引入】
(1)如图①,在Rt△ABC中,∠A=90°,若沿直线l剪去∠A,则∠1+∠2=__________;
(2)如图②,在△ABC中,∠A=40°,若剪去∠A,则∠1+∠2=__________;
【类比探究】
(3)如图③,在△ABC中,若∠A=α,剪去∠A后得到∠1和∠2,请你猜想∠1+∠2与∠A的数量关系:__________________;
【知识拓展】
(4)如图④,在△ABC中,将∠A折叠,使点A落在△ABC内的点P处,试猜想∠1+∠2与∠A的数量关系,并说明理由.
题23图
1.B 2.A 3.D 4.C 5.C 6.B 7.C 8.B 9.A 10.C
11.3<x<13 12.85° 13.12 14.360° 15.①②③
16.解:∵∠B=50°,∠ANC=80°,∴∠BAN=∠ANC-∠B=80°-50°=30°.
∵AN是∠BAC的平分线,∴∠BAC=2∠BAN=60°.
∴∠C=180°-∠B-∠BAC=70°.
17.解:设这个多边形的边数是n,则内角和为(n-2)×180°.
依题意,得(n-2)×180°=2×360°+180°.解得n=7.
∴这个多边形的边数是7.
18.解:∵AD,CE是△ABC的两条高,∴S△ABC=AB·CE=BC·AD.
∵AB=4,BC=8,CE=6,∴×4×6=×8·AD.∴AD=3 cm.
19.解:设∠1=∠2=x,则∠3=∠4=∠1+∠2=2x.
∵∠BAC=72°,∴∠2+∠4=180°-∠BAC=108°,即x+2x=108°.
∴x=36°.∴∠1=∠2=36°.∴∠ADB=180°-∠1-∠2=108°.
20.解:由题意,得∠BAC=50°+15°=65°,∠ABC=85°-50°=35°.
∴∠ACB=180°-∠BAC-∠ABC=180°-65°-35°=80°.
答:从C村观测A,B两个村庄的视角∠ACB的度数为80°.
21.解:(1)设底边长为x cm,则腰长为2x cm.
∵等腰三角形的周长是25 cm,∴2x+2x+x=25.∴x=5,2x=10.
∴各边的长分别为10 cm,10 cm,5 cm.
(2)①当底边长为6 cm时,腰长为(25-6)÷2=9.5(cm).
此时另两边的长分别为9.5 cm,9.5 cm,能构成三角形.
②当腰长为6 cm时,底边长为25-6×2=13(cm).
∵6+6=12<13,∴此时不能构成三角形.
综上,另两边的长分别为9.5 cm,9.5 cm.
22.(1)解:∵CD是高,∠DCB=40°,∴∠B=90°-∠DCB=50°.
∵∠ACB=90°,∴∠BAC=90°-∠B=40°.
∵AE是角平分线,∴∠BAE=∠BAC=20°.
∴∠CEF=∠B+∠BAE=50°+20°=70°.
(2)证明:∵∠ACB=90°,CD是高,∴∠CAE+∠AEC=90°,∠FAD+∠AFD=90°.
∵AE是角平分线,∴∠CAE=∠FAD.∴∠AEC=∠AFD.
又∠AFD=∠CFE,∴∠CEF=∠CFE.
23.解:(1)270°.(2)220°.(3)∠1+∠2=180°+∠A.
(4)∠1+∠2=2∠A.理由如下:
∠1+∠2=180°×2-2(180°-∠A)=360°-360°+2∠A=2∠A,即∠1+∠2=2∠A.
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题10小题,每小题3分,共30分)
1.下列长度的三条线段,能组成三角形的是( )
A.2,2,4 B.4,5,8 C.3,6,9 D.5,5,11
2.安装空调时,一般会采用如图所示的方法固定,这样做的数学依据是( )
题2图
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,在△ABC中,边AC上的高是( )
题3图
A.线段AE B.线段CD C.线段AF D.线段BF
4.一个多边形的内角和为1 260°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
5.在△ABC中,若∠A∶∠B∶∠C=2∶3∶5,则该三角形的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
6.如图,已知Rt△ABC和Rt△DEF,∠D=∠ACB=90°,∠A=30°,∠F=45°,A,E,B,D四点在一条直线上,点C在EF上,则∠ECB的度数为( )
题6图
A.70° B.75° C.80° D.85°
7.如图,已知AD是△ABC的中线,CE是△ACD的中线,S△ACE=4,则S△ABC=( )
题7图
A.14 B.15 C.16 D.17
8.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=32°,∠CAD=24°,则∠B=( )
题8图
A.45° B.50° C.55° D.60°
9.(2023深圳)如图为商场某品牌椅子及其侧面示意图,∠DEF=120°,DE与地面平行,∠ABD=50°,则∠ACB=( )
题9图
A.70° B.65° C.60° D.50°
10.科技馆为某机器人编制了一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
题10图
A.6米 B.8米 C.10米 D.12米
二、填空题(本大题5小题,每小题3分,共15分)
11.已知三角形的三边长分别为5,x,8,则x的取值范围是__________.
12.在△ABC中,∠B=70°,∠C=25°,则∠A=__________.
13.如图,已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4 cm.若AB=16 cm,则AC=__________cm.
题13图
14.如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为__________.
题14图
15.如图,∠ABC=∠ACB,AD,BD,CD分别是∠CAE,∠ABC,∠ACF的平分线.下列结论:①AD∥BC;②∠BDC=∠BAC;③∠ADC+∠ABD=90°;④BD平分∠ADC.其中正确的是__________.(填序号)
题15图
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.如图,在△ABC中,AN是∠BAC的平分线,∠B=50°,∠ANC=80°.求∠C的度数.
题16图
17.一个多边形的内角和比它的外角和的2倍多180°,求这个多边形的边数.
18.如图,AD,CE是△ABC的两条高,AB=4 cm,BC=8 cm,CE=6 cm,求AD的长.
题18图
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=72°,求∠1和∠ADB的度数.
题19图
20.如图,已知B村在A村的南偏西50°方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A,B两个村庄的视角∠ACB的度数.
题20图
21.一个等腰三角形的周长为25 cm.
(1)若腰长是底边长的2倍,求各边的长;
(2)若其中一边的长为6 cm,求另两边的长.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE,CD相交于点F.
(1)若∠DCB=40°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
题22图
23.综合与实践
学习三角形内角和定理后,我们知道,任何一个三角形的三个内角之和都等于180°.请利用三角形内角和定理,解决以下问题:
【问题引入】
(1)如图①,在Rt△ABC中,∠A=90°,若沿直线l剪去∠A,则∠1+∠2=__________;
(2)如图②,在△ABC中,∠A=40°,若剪去∠A,则∠1+∠2=__________;
【类比探究】
(3)如图③,在△ABC中,若∠A=α,剪去∠A后得到∠1和∠2,请你猜想∠1+∠2与∠A的数量关系:__________________;
【知识拓展】
(4)如图④,在△ABC中,将∠A折叠,使点A落在△ABC内的点P处,试猜想∠1+∠2与∠A的数量关系,并说明理由.
题23图
1.B 2.A 3.D 4.C 5.C 6.B 7.C 8.B 9.A 10.C
11.3<x<13 12.85° 13.12 14.360° 15.①②③
16.解:∵∠B=50°,∠ANC=80°,∴∠BAN=∠ANC-∠B=80°-50°=30°.
∵AN是∠BAC的平分线,∴∠BAC=2∠BAN=60°.
∴∠C=180°-∠B-∠BAC=70°.
17.解:设这个多边形的边数是n,则内角和为(n-2)×180°.
依题意,得(n-2)×180°=2×360°+180°.解得n=7.
∴这个多边形的边数是7.
18.解:∵AD,CE是△ABC的两条高,∴S△ABC=AB·CE=BC·AD.
∵AB=4,BC=8,CE=6,∴×4×6=×8·AD.∴AD=3 cm.
19.解:设∠1=∠2=x,则∠3=∠4=∠1+∠2=2x.
∵∠BAC=72°,∴∠2+∠4=180°-∠BAC=108°,即x+2x=108°.
∴x=36°.∴∠1=∠2=36°.∴∠ADB=180°-∠1-∠2=108°.
20.解:由题意,得∠BAC=50°+15°=65°,∠ABC=85°-50°=35°.
∴∠ACB=180°-∠BAC-∠ABC=180°-65°-35°=80°.
答:从C村观测A,B两个村庄的视角∠ACB的度数为80°.
21.解:(1)设底边长为x cm,则腰长为2x cm.
∵等腰三角形的周长是25 cm,∴2x+2x+x=25.∴x=5,2x=10.
∴各边的长分别为10 cm,10 cm,5 cm.
(2)①当底边长为6 cm时,腰长为(25-6)÷2=9.5(cm).
此时另两边的长分别为9.5 cm,9.5 cm,能构成三角形.
②当腰长为6 cm时,底边长为25-6×2=13(cm).
∵6+6=12<13,∴此时不能构成三角形.
综上,另两边的长分别为9.5 cm,9.5 cm.
22.(1)解:∵CD是高,∠DCB=40°,∴∠B=90°-∠DCB=50°.
∵∠ACB=90°,∴∠BAC=90°-∠B=40°.
∵AE是角平分线,∴∠BAE=∠BAC=20°.
∴∠CEF=∠B+∠BAE=50°+20°=70°.
(2)证明:∵∠ACB=90°,CD是高,∴∠CAE+∠AEC=90°,∠FAD+∠AFD=90°.
∵AE是角平分线,∴∠CAE=∠FAD.∴∠AEC=∠AFD.
又∠AFD=∠CFE,∴∠CEF=∠CFE.
23.解:(1)270°.(2)220°.(3)∠1+∠2=180°+∠A.
(4)∠1+∠2=2∠A.理由如下:
∠1+∠2=180°×2-2(180°-∠A)=360°-360°+2∠A=2∠A,即∠1+∠2=2∠A.
