人教版2024-2025九年级数学上册同步讲义专题专题24.1圆【十大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025九年级数学上册同步讲义专题专题24.1圆【十大题型】(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 00:00:00 | ||
图片预览



文档简介
专题24.1 圆【十大题型】
【人教版】
【题型1 圆的基本概念】 1
【题型2 识别圆心角】 2
【题型3 求圆中弦的条数】 3
【题型4 圆的周长和面积】 4
【题型5 确定圆内一点最长的弦】 5
【题型6 判断点与圆的位置关系】 6
【题型7 由点与圆的位置关系求半径】 7
【题型8 求一点到圆上点的距离的最值】 8
【题型9 圆中角度的计算】 9
【题型10 圆中线段长度的计算】 10
知识点1:圆的有关概念
圆的定义:第一种:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫作圆。固定的端点O叫作圆心,线段OA叫作半径。
第二种:圆心为O,半径为r的圆可以瞧成就是所有到定点O的距离等于定长r的点的集合。
比较圆的两种定义可知:第一种定义就是圆的形成进行描述的,第二种就是运用集合的观点下的定义,但就是都说明确定了定点与定长,也就确定了圆。
弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫作直径。
弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。小于半圆的弧叫做劣弧。大于半圆的弧叫做优弧。
等圆:等够重合的两个圆叫做等圆。
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
弦就是线段,弧就是曲线,判断等弧首要的条件就是在同圆或等圆中,只有在同圆或等圆中完全重合的弧才就是等弧,而不就是长度相等的弧。
同圆或等圆的半径相等.
【题型1 圆的基本概念】
【例1】(23-24九年级·山东潍坊·期末)下列说法正确的有( )
A.经过圆心的线段是直径 B.直径是同一个圆中最长的弦
C.长度相等的两条弧是等弧 D.弧分为优弧和劣弧
【变式1-1】(23-24·甘肃平凉·模拟预测)如图, 的两条弦、的延长线交于C点,的平分线过点O,请直接写出图中一对相等的线段: .
【变式1-2】(23-24·湖南常德·一模)如图,在平面直角坐标系中,点A的坐标为,点B在y轴正半轴上,以点B为圆心,长为半径作弧,交x轴正半轴于点C,则点C的坐标为 .
【变式1-3】(23-24·河北邯郸·二模)如图,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
知识点2:圆心角
顶点在圆心的角叫圆心角.
【题型2 识别圆心角】
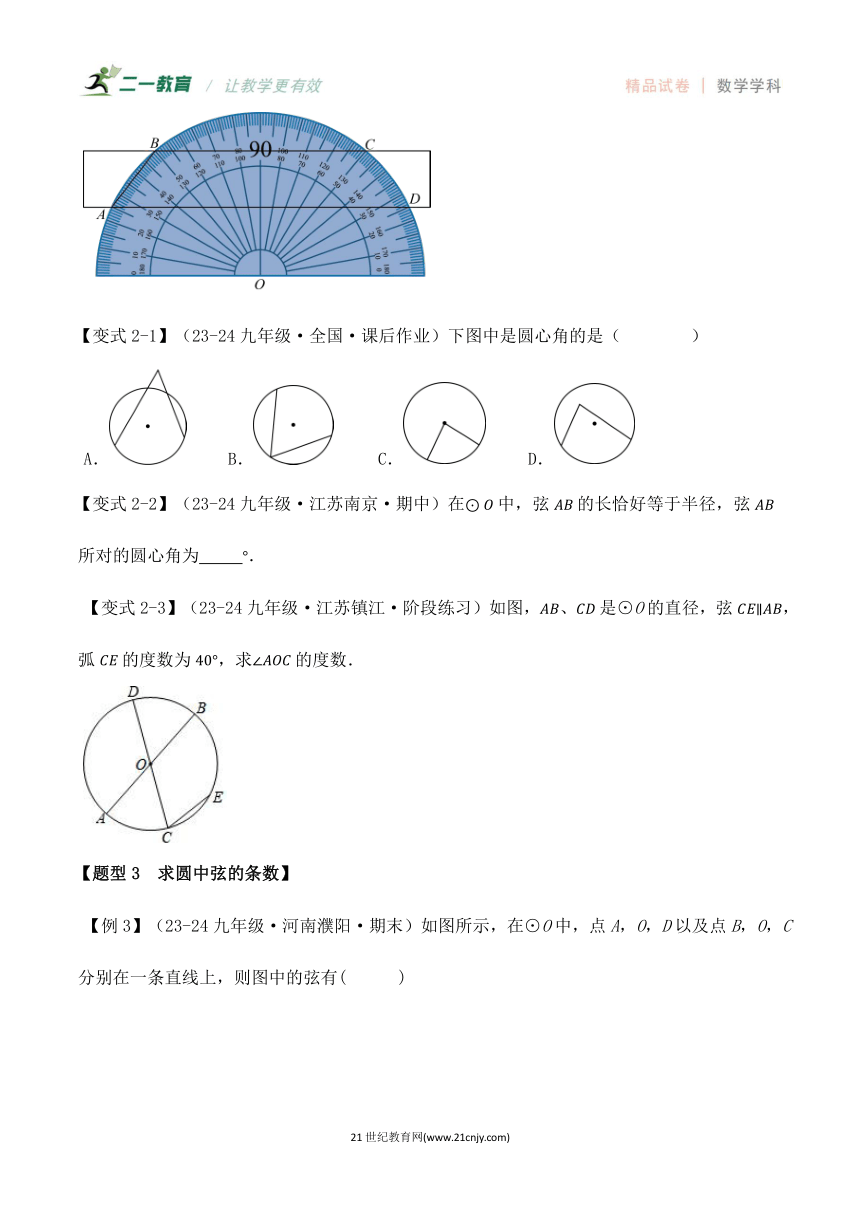
【例2】(23-24·山东烟台·中考真题)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接,则的度数为 .
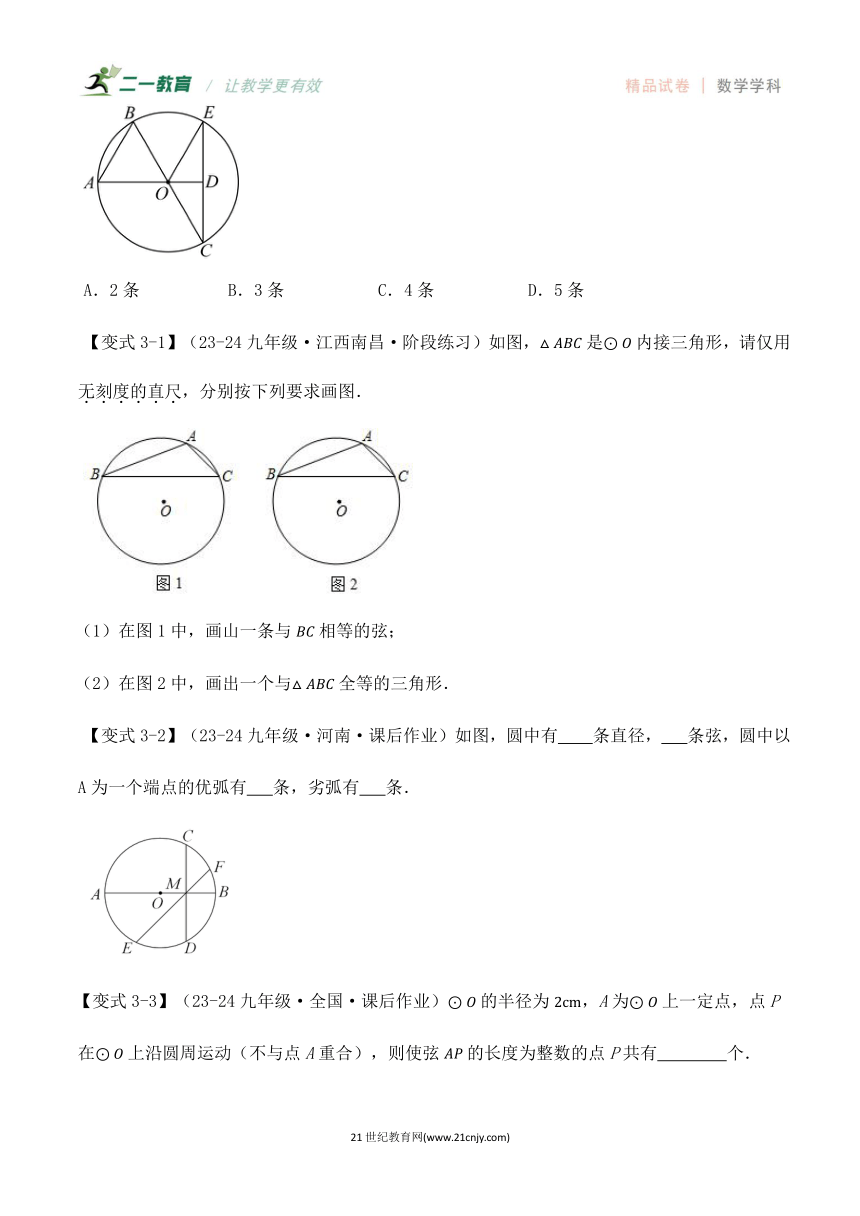
【变式2-1】(23-24九年级·全国·课后作业)下图中是圆心角的是( )
A. B. C. D.
【变式2-2】(23-24九年级·江苏南京·期中)在中,弦的长恰好等于半径,弦所对的圆心角为 .
【变式2-3】(23-24九年级·江苏镇江·阶段练习)如图,、是⊙O的直径,弦,弧的度数为,求的度数.
【题型3 求圆中弦的条数】
【例3】(23-24九年级·河南濮阳·期末)如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
【变式3-1】(23-24九年级·江西南昌·阶段练习)如图,是内接三角形,请仅用无刻度的直尺,分别按下列要求画图.
(1)在图1中,画山一条与相等的弦;
(2)在图2中,画出一个与全等的三角形.
【变式3-2】(23-24九年级·河南·课后作业)如图,圆中有 条直径, 条弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
【变式3-3】(23-24九年级·全国·课后作业)的半径为,A为上一定点,点P在上沿圆周运动(不与点A重合),则使弦的长度为整数的点P共有 个.
【题型4 圆的周长和面积】
【例4】(23-24九年级·山东潍坊·期末)由所有到已知点O的距离不小于3,并且不大于5的点组成的图形的面积为 .
【变式4-1】(23-24九年级·上海静安·期末)如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
【变式4-2】(23-24九年级·福建厦门·期末)如图,长方形ABCD的面积为225,长和宽的比为5∶3,在此长方形内沿着边的方向能否并排裁出两个面积均为的圆(取3),请通过计算说明理由.
【变式4-3】(23-24九年级·湖北武汉·期末)如图,是编号为1、2、3、4的400m跑道,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每条跑道宽1m,内侧的1号跑道长度为400m,则2号跑道比1号跑道长 m;若在一次200m比赛中(每个跑道都由一个半圆形跑道和部分直跑道组成),要使得每个运动员到达同一终点线,则4号跑道起跑点比2号跑道起跑点应前移 m(π取3.14).
【题型5 确定圆内一点最长的弦】
【例5】(23-24·广东深圳·二模)如图(a),A,B是⊙O上两定点,,圆上一动点P从点B出发,沿逆时针方向匀速运动到点A,运动时间是,线段AP的长度是.图(b)是y随x变化的关系图象,其中图象与x轴交点的横坐标记为m,则m的值是( )
A.8 B.6 C. D.
【变式5-1】(23-24九年级·河南周口·期末)若的直径长为,点,在上,则的长不可能是( )
A.2 B.3 C.4 D.5
【变式5-2】(23-24九年级·浙江杭州·阶段练习)如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
【变式5-3】(23-24九年级·江苏宿迁·期中)如图,的半径为5,弦的长为6,延长至点,使得点为的中点,在上任取一点,连接、,则的最大值为( )
A.290 B.272 C.252 D.244
知识点3:点与圆的位置关系
设⊙O的半径为r,点P到圆心的距离为OP=d,则有:
点P在圆外d>r;
点P在圆上d=r;
点P在圆内d<r.
【题型6 判断点与圆的位置关系】
【例6】(23-24九年级·安徽阜阳·期末)在平面内,的半径为,点到圆心的距离为,则点与的位置关系是点在 .(填“圆内”“圆外”或“圆上”).
【变式6-1】(23-24九年级·广东湛江·期末)如图,在中,,点D在边上,且,以为直径作,设线段的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
【变式6-2】(23-24九年级·北京海淀·期末)如图,,,是某社区的三栋楼,若在中点处建一个基站,其覆盖半径为200m,则这三栋楼中在该基站覆盖范围内的是( )
A.,,都不在 B.只有 C.只有, D.,,
【变式6-3】(23-24九年级·浙江宁波·期末)如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
【题型7 由点与圆的位置关系求半径】
【例7】(23-24九年级·北京顺义·期末)已知矩形中, ,,以点B为圆心r为半径作圆,且与边有唯一公共点,则r的取值范围是 .
【变式7-1】(23-24九年级·山东烟台·期末)点P是⊙O所在平面内一点,若⊙O的面积为,则当OP 时,点P-定在⊙O的外部.
【变式7-2】(23-24九年级·江苏南通·期中)在数轴上,点A所表示的实数为4,点B所表示的实数为b,的半径为2,要使点B在内时,实数b的取值范围是( )
A. B. C.或 D.
【变式7-3】(23-24九年级·上海·专题练习)如图,在中,,,,点在边上,,的半径长为,与相交,且点在外,那么的半径长可能是( )
A. B. C. D.
【题型8 求一点到圆上点的距离的最值】
【例8】(23-24·陕西·模拟预测)如图,在矩形中,,, 是平面内一动点,且,则线段的最大值为 .
【变式8-1】(23-24·河南郑州·三模)如图,点M是等边三角形边的中点,P是三角形内一点,连接,将线段以A为中心逆时针旋转得到线段,连接.若,,则的最小值为 .
【变式8-2】(23-24九年级·湖北武汉·期中)如图,已知在中,,,将绕点A逆时针旋转.得到.点D是边的中点,点E为边上的动点,在绕点A逆时针旋转的过程中,点E的对应点是点,则线段长度的最大值与最小值的差是 .
【变式8-3】(23-24九年级·江苏镇江·阶段练习)如图,正比例函数与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的上运动,点Q是的中点,则长的最大值为( )
A. B. C. D.
【题型9 圆中角度的计算】
【例9】(23-24九年级·广东珠海·期末)如图,在平面直角坐标系中,B,C为x轴上两点,以点O为圆心画圆(直径小于),交y轴负半轴于点A,过点A作x轴平行线,点P为圆上一个动点,连接,下列说法正确的有( )
①当点P运动到第一象限,则
②当点P运动到第二象限,则
③当点P运动到第三象限,则
④当点P运动到第四象限,则
A.①② B.③④ C.①④ D.②③
【变式9-1】(23-24九年级·江苏连云港·阶段练习)如图,的圆心为点,以点为圆心作,且与的延长线交于点,与的延长线交于点.已知,求的度数.
【变式9-2】(23-24九年级·湖南湘西·期中)如图,是半圆的直径,点是半圆上不与点、重合的一个动点,延长到点,使,是的中点,连接、.
(1)求证: ;
(2)连接,当四边形是菱形时,求的度数.
【变式9-3】(23-24·湖北武汉·一模)如图,在中,,C为上一点,连接.
(1)若,求的度数;
(2)若的面积与的面积之比为,求的值.
【题型10 圆中线段长度的计算】
【例10】(23-24·上海虹口·二模)如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A的对称点),那么的长为 .
【变式10-1】(23-24九年级·山东滨州·期中)如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D,若点D巧好为线段AB的中点,则AB的长度为( )
A. B.3 C. 6 D.9
【变式10-2】(23-24九年级·浙江绍兴·期末)如图,正方形的边长为4,点在边上,,点在上,与直线交于点(点在点右侧),则的长度为( )
A. B.8 C. D.
【变式10-3】(23-24·广东江门·模拟预测)综合探究
如图,在扇形中,是上异于的动点,过点作于点,作于点,连接,点在线段上,且.
(1)求证:四边形是平行四边形.
(2)当点在上运动时,在中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.
(3)求证:是定值.21世纪教育网(www.21cnjy.com)
专题24.1 圆【十大题型】
【人教版】
【题型1 圆的基本概念】 1
【题型2 识别圆心角】 4
【题型3 求圆中弦的条数】 7
【题型4 圆的周长和面积】 10
【题型5 确定圆内一点最长的弦】 13
【题型6 判断点与圆的位置关系】 16
【题型7 由点与圆的位置关系求半径】 20
【题型8 求一点到圆上点的距离的最值】 22
【题型9 圆中角度的计算】 27
【题型10 圆中线段长度的计算】 32
知识点1:圆的有关概念
圆的定义:第一种:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫作圆。固定的端点O叫作圆心,线段OA叫作半径。
第二种:圆心为O,半径为r的圆可以瞧成就是所有到定点O的距离等于定长r的点的集合。
比较圆的两种定义可知:第一种定义就是圆的形成进行描述的,第二种就是运用集合的观点下的定义,但就是都说明确定了定点与定长,也就确定了圆。
弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫作直径。
弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。小于半圆的弧叫做劣弧。大于半圆的弧叫做优弧。
等圆:等够重合的两个圆叫做等圆。
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
弦就是线段,弧就是曲线,判断等弧首要的条件就是在同圆或等圆中,只有在同圆或等圆中完全重合的弧才就是等弧,而不就是长度相等的弧。
同圆或等圆的半径相等.
【题型1 圆的基本概念】
【例1】(23-24九年级·山东潍坊·期末)下列说法正确的有( )
A.经过圆心的线段是直径 B.直径是同一个圆中最长的弦
C.长度相等的两条弧是等弧 D.弧分为优弧和劣弧
【答案】B
【分析】本题考查了圆的相关概念,解题的关键是掌握直径的定义,弧的定义,弧的分类,根据相关概念,逐个判断即可.
【详解】解:A、经过圆心,且两端点在圆上的线段是直径,故A不正确,不符合题意;
B、直径是同一个圆中最长的弦,故B正确,符合题意;
C、在同圆或等圆中,长度相等的两条弧是等弧,故C不正确,不符合题意;
D、弧分为优弧、劣弧和半圆,故D不正确,不符合题意;
故选:B.
【变式1-1】(23-24·甘肃平凉·模拟预测)如图, 的两条弦、的延长线交于C点,的平分线过点O,请直接写出图中一对相等的线段: .
【答案】(或或)
【分析】根据圆是轴对称图形,对称轴是经过圆心的每一条直线;角是轴对称图形,对称轴是角平分线所在的直线结合进行判断.此题关键是根据图形的对称性,分析可以重合的线段.
【详解】这个图形是轴对称图形,对称轴即是直线,根据轴对称的性质,得或或.
故答案为:(或或).
【变式1-2】(23-24·湖南常德·一模)如图,在平面直角坐标系中,点A的坐标为,点B在y轴正半轴上,以点B为圆心,长为半径作弧,交x轴正半轴于点C,则点C的坐标为 .
【答案】
【分析】本题考查了同圆半径相等、等腰三角形的三线合一、点坐标等知识点.连接,先根据点的坐标可得,再根据等腰三角形的判定可得是等腰三角形,然后根据等腰三角形的三线合一可得,由此即可得出答案.
【详解】解:如图,连接,
点的坐标为,
,
由同圆半径相等得:,
是等腰三角形,
,
(等腰三角形的三线合一),
又点位于轴正半轴,
点的坐标为,
故答案为:.
【变式1-3】(23-24·河北邯郸·二模)如图,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
【答案】D
【分析】本题主要考查圆的性质和平行四边形的判定,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,可得,故可判断四边形是平行四边形
【详解】解:在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,
∴,
∴四边形是平行四边形
故选:D
知识点2:圆心角
顶点在圆心的角叫圆心角.
【题型2 识别圆心角】
【例2】(23-24·山东烟台·中考真题)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接,则的度数为 .
【答案】
【分析】方法一∶如图:连接,由题意可得:,,然后再根据等腰三角形的性质求得、,最后根据角的和差即可解答.
方法二∶ 连接,由题意可得:,然后根据圆周角定理即可求解.
【详解】方法一∶ 解:如图:连接,
由题意可得:,,,
∴,,
∴.
故答案为.
方法二∶解∶ 连接,
由题意可得:,
根据圆周角定理,知.
故答案为.
【点睛】本题主要考查了角的度量、圆周角定理等知识点,掌握圆周角的度数等于它所对弧上的圆心角度数的一半是解答本题的关键.
【变式2-1】(23-24九年级·全国·课后作业)下图中是圆心角的是( )
A. B. C. D.
【答案】C
【分析】根据圆心角的概念:圆心角是指在中心为O的圆中,过弧AB两端的半径构成的∠AOB, 称为弧AB所对的圆心角进行判断.
【详解】解:A、不是圆心角,故不符合题意;
B、不是圆心角,故不符合题意;
C、是圆心角,故符合题意;
D、不是圆心角,故不符合题意;
故选:C.
【点睛】本题考查的是圆心角的概念,掌握顶点在圆心的角叫作圆心角是解题的关键.
【变式2-2】(23-24九年级·江苏南京·期中)在中,弦的长恰好等于半径,弦所对的圆心角为 .
【答案】60
【分析】本题考查了圆心角、等边三角形的判定与性质,熟练掌握圆心角是解题关键.根据等边三角形的判定与性质可得,由此即可得.
【详解】解:如图,∵在中,弦的长恰好等于半径,
,
是等边三角形,
,
即弦所对的圆心角为,
故答案为:60.
【变式2-3】(23-24九年级·江苏镇江·阶段练习)如图,、是⊙O的直径,弦,弧的度数为,求的度数.
【答案】
【分析】连接,由弧的度数为,得到,根据等腰三角形的性质和三角形的内角和定理可求出,再由,即可得到.
【详解】解:连接,如图,
∵弧的度数为,
∴,
∵,
∴,
∴,
∵弦,
∴.
【点睛】本题考查了圆的基本性质,等腰三角形的性质,三角形内角和定理以及平行线的性质,熟练掌握圆的基本性质是解题的关键.
【题型3 求圆中弦的条数】
【例3】(23-24九年级·河南濮阳·期末)如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
【答案】B
【分析】根据弦的定义进行分析,从而得到答案.
【详解】解:图中的弦有AB,BC,CE共三条,
故选B.
【点睛】本题主要考查了弦的定义,熟知定义是解题的关键:连接圆上任意两点的线段叫弦.
【变式3-1】(23-24九年级·江西南昌·阶段练习)如图,是内接三角形,请仅用无刻度的直尺,分别按下列要求画图.
(1)在图1中,画山一条与相等的弦;
(2)在图2中,画出一个与全等的三角形.
【答案】(1)见解析;(2)见解析
【分析】(1)连结CO并延长交于E,连接BO并延长交于D,连结ED,再证△BOC≌△DOE(SAS),可得BC=DE;
(2)连结AO并延长交于A′,OA=OA′,连结BO并延长交于B′,OB=OB′,连结CO并延长交于C′,OC=OC′,利用边角边判定方法先证△BOC≌△B′OC′(SAS),可得BC=B′C′;同理可证△BOA≌△B′OA′(SAS),可得AB=A′B′,同理可证△AOC≌△A′OC′(SAS),可得AC=A′C′,利用三边对应相等判定方法可证△ABC≌△A′B′C′(SSS).
【详解】解:(1)如图1,DE为所作;
连结CO并延长交于E,连接BO并延长交于D,连结ED,
∵OB=OD=OE=OC,
在△BOC和△DOE中,
,
∴△BOC≌△DOE(SAS),
∴BC=DE;
(2)如图2,△A′B′C′为所作.
连结AO并延长交于A′,OA=OA′,连结BO并延长交于B′,OB=OB′,连结CO并延长交于C′,OC=OC′,
在△BOC和△B′OC′中,
,
∴△BOC≌△B′OC′(SAS),
∴BC=B′C′;
同理可证△BOA≌△B′OA′(SAS),
∴AB=A′B′,
同理可证△AOC≌△A′OC′(SAS),
∴AC=A′C′,
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(SSS).
【点睛】本题考查仅用无刻度的直尺画线段,画三角形,三角形全等判定与性质,圆的性质,掌握圆的性质与三角形全等判定与性质是解题关键.
【变式3-2】(23-24九年级·河南·课后作业)如图,圆中有 条直径, 条弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
【答案】 1 3 4 4
【详解】圆中有AB一条直径,AB、CD、EF三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条,
故答案为1,3,4,4.
【变式3-3】(23-24九年级·全国·课后作业)的半径为,A为上一定点,点P在上沿圆周运动(不与点A重合),则使弦的长度为整数的点P共有 个.
【答案】7
【分析】本题主要考查了圆的弦的概念.熟练掌握圆的弦的定义和性质,是解决问题的关键.圆的弦的定义:连接圆上任意两点间的线段叫做弦.最大弦是直径.
根据的半径为,得到直径,根据,得到在半圆上,有3个,另一侧也有3个,加上长度为的是与B点重合,一共有7个.
【详解】如图,∵的半径为,
∴直径,
∴弦长的整数值有或或或,共4种可能,
当或或时,各有2条,
当时有1条,
∴这样的弦共有7条.
∴这样的点P共有7个.
故答案为:7.
【题型4 圆的周长和面积】
【例4】(23-24九年级·山东潍坊·期末)由所有到已知点O的距离不小于3,并且不大于5的点组成的图形的面积为 .
【答案】
【分析】根据题意调查到点的距离不小于3,并且不大于5的点组成的图形是半径为5和半径为所组成的环形面积即可.本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
【详解】解:如图,
到点的距离不小于3,并且不大于5的点组成的图形是图中环形,
所以
.
故答案为:.
【变式4-1】(23-24九年级·上海静安·期末)如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
【答案】
【分析】设小圆的半径为r,则大圆的半径为,根据,列方程求得大圆和小圆的半径,再计算大圆和小圆的周长之和即可求解.
【详解】解:设小圆的半径为r,则大圆的半径为,
由图可得,,即,
解得, (舍),,
∴,
∴,
答:围成圆环铁丝的总长度为.
【变式4-2】(23-24九年级·福建厦门·期末)如图,长方形ABCD的面积为225,长和宽的比为5∶3,在此长方形内沿着边的方向能否并排裁出两个面积均为的圆(取3),请通过计算说明理由.
【答案】不能并排裁出两个面积均为75cm2的圆,理由见解析
【分析】根据长方形的长宽比设长方形的长AB为5x cm,宽AD为3x cm,结合长方形ABCD的面积为225,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积为,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
【详解】解:设长方形的长AB为5x cm,宽AD为3x cm,
根据题意得,
解得(负值舍弃),
∴,
∴,,
∵圆的面积为75,设圆的半径为rcm,
∴,
解得,
∴,
∵,
∴不能并排裁出两个面积均为75cm2的圆.
【点睛】本题考查了解一元二次方程、圆的面积以及实数大小的比较,解题关键是求出圆的半径以及长方形的长.
【变式4-3】(23-24九年级·湖北武汉·期末)如图,是编号为1、2、3、4的400m跑道,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每条跑道宽1m,内侧的1号跑道长度为400m,则2号跑道比1号跑道长 m;若在一次200m比赛中(每个跑道都由一个半圆形跑道和部分直跑道组成),要使得每个运动员到达同一终点线,则4号跑道起跑点比2号跑道起跑点应前移 m(π取3.14).
【答案】 6.28 6.28
【分析】利用各跑道直线跑道相等,每条跑道宽1m,两个半圆相加得一个整圆列出式子对比即可.
【详解】解:设直线部分长为l米
1号:
2号:
3号:
4号:
2号比1号长:
4号起点比2号起点前移:
故答案为:6.28,6.28
【点睛】本题考查了列代数式,圆的周长公式,整式的加减等知识点,熟练掌握是解题的关键.
【题型5 确定圆内一点最长的弦】
【例5】(23-24·广东深圳·二模)如图(a),A,B是⊙O上两定点,,圆上一动点P从点B出发,沿逆时针方向匀速运动到点A,运动时间是,线段AP的长度是.图(b)是y随x变化的关系图象,其中图象与x轴交点的横坐标记为m,则m的值是( )
A.8 B.6 C. D.
【答案】B
【分析】本题考查了动点问题的函数图形,合理分析动点的运动时间是解题关键.
根据最长时经过的路程所用的运动时间,求出总路程所用的时间是之前的三倍,即可解答.
【详解】解:如图,当点运动到过圆心,即为直径时,最长,
由图(b)得,最长时为6,此时,
,
,
此时点路程为90度的弧,
点从点运动到点的弧度为270度,
运动时间为,
故选:B.
【变式5-1】(23-24九年级·河南周口·期末)若的直径长为,点,在上,则的长不可能是( )
A.2 B.3 C.4 D.5
【答案】D
【分析】根据直径是最长的弦即可求解.
【详解】解:∵若的直径长为,点,在上,
∴的长不可能是,
故选:D.
【点睛】本题考查了圆的相关概念,掌握直径是最长的弦是解题的关键.
【变式5-2】(23-24九年级·浙江杭州·阶段练习)如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
【答案】2
【分析】如图,连接并延长,交圆于点D,连接,由中位线定理,得,点A为定点,C为动点,的最大值为直径长,即长.于是的最大值为.
【详解】解:如图,连接并延长,交圆于点D,连接,
∵点M,N分别是AB,BC中点,
∴.
点A为定点,C为动点,的最大值为直径长,即长.
∵是直径,
∴.
∴的最大值为.
故答案为:2
【点睛】本题考查中位线定理,圆的基本概念弦与直径;掌握中位线定理是解题的关键.
【变式5-3】(23-24九年级·江苏宿迁·期中)如图,的半径为5,弦的长为6,延长至点,使得点为的中点,在上任取一点,连接、,则的最大值为( )
A.290 B.272 C.252 D.244
【答案】B
【分析】本题考查了勾股定理,圆内最长弦是直径,过点C作于点N,连接,根据勾股定理可得 ,,利用弦最长等于直径即可得出答案.
【详解】解:过点C作于点N,连接,
点为的中点,,
,
,
,
,
,
当最大时,最大,
在中,
,
当最大时,最大,
的半径为5,
弦最长等于直径是10,
,
.
故选:B.
知识点3:点与圆的位置关系
设⊙O的半径为r,点P到圆心的距离为OP=d,则有:
点P在圆外d>r;
点P在圆上d=r;
点P在圆内d<r.
【题型6 判断点与圆的位置关系】
【例6】(23-24九年级·安徽阜阳·期末)在平面内,的半径为,点到圆心的距离为,则点与的位置关系是点在 .(填“圆内”“圆外”或“圆上”).
【答案】圆外
【分析】本题考查了点与圆的位置关系,设的半径为,点到圆心的距离,则有:点在圆外;点在圆上;点在圆内;据此即可判断求解,掌握点与圆的位置关系是解题的关键.
【详解】解:∵的半径为,点到圆心的距离为,
∴,
∴点在圆外,
故答案为:圆外.
【变式6-1】(23-24九年级·广东湛江·期末)如图,在中,,点D在边上,且,以为直径作,设线段的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
【答案】C
【分析】本题考查了对点与圆的位置关系的判断,三角形中位线定理等知识.关键要记住若半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.首先根据三角形中位线的性质得出,进而利用点与圆的位置关系得出即可.
【详解】解:连接,
∵以为直径作,线段的中点为P,
∴是的中位线,
∴,
∵,
∴,
∴点P与的位置关系是点P在外.
故选:C.
【变式6-2】(23-24九年级·北京海淀·期末)如图,,,是某社区的三栋楼,若在中点处建一个基站,其覆盖半径为200m,则这三栋楼中在该基站覆盖范围内的是( )
A.,,都不在 B.只有 C.只有, D.,,
【答案】A
【分析】
根据勾股定理的逆定理证得是直角三角形,可以根据直角三角形斜边中线的性质求得的长,然后与比较大小,即可解答本题.本题考查勾股定理的逆定理,直角三角形斜边上的中线的性质,点D与圆的位置关系,解题的关键是求出三角形三个顶点到点的距离.
【详解】
解:,,,
,
是直角三角形,且,
点是斜边的中点,
,,
如图,以为圆心,为半径画圆,
,
点A,B,C都不在覆盖范围内,
故选:A.
【变式6-3】(23-24九年级·浙江宁波·期末)如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
【答案】A
【分析】根据等腰三角形的性质求出BD=CD=6cm,利用勾股定理求出AD,得到AP的长,即可判断点A与的位置关系;利用勾股定理求出BP、CP,即可判断点B、C与的位置关系,由DP即可判断点D与位置关系.
【详解】解:∵,
∴BD=CD=6cm,∠ADC=90°,
∴cm,
∵DP=2cm,
∴AP=6cm,
∴点A在上;故A选项符合题意;
连接BP、CP,
∵,
∴AD垂直平分BC,
∴BP=CP=,
∴点B、C都在外;故B、C选项都不符合题意;
∵DP=2<6,
∴点在内,故D选项不符合题意,
故选:A.
【点睛】此题考查了点与圆的位置关系,勾股定理,线段垂直平分线的判定及性质,等腰三角形三线合一的性质,熟记点与圆的位置关系是解题的关键.
【题型7 由点与圆的位置关系求半径】
【例7】(23-24九年级·北京顺义·期末)已知矩形中, ,,以点B为圆心r为半径作圆,且与边有唯一公共点,则r的取值范围是 .
【答案】
【分析】连接,,利用勾股定理求出的长,抓住已知以点B为圆心r为半径作圆,且与边有唯一公共点,就可求出的半径r的取值范围.
【详解】解:连接,,
∵矩形中,,,
∴,,,
∵以点B为圆心作圆,与边有唯一公共点,
∴的半径r的取值范围是:;
故答案为:.
【点睛】此题考查了点与圆的位置关系以及矩形的性质,勾股定理.注意若半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.
【变式7-1】(23-24九年级·山东烟台·期末)点P是⊙O所在平面内一点,若⊙O的面积为,则当OP 时,点P-定在⊙O的外部.
【答案】>3
【分析】由⊙O的面积为9π,可求出半径为3,再根据点P在圆外d>r可得解.
【详解】解:设⊙O的半径为r,
∵⊙O的面积为9π,
∴,
∴r=3,
∴⊙O的半径为3,
∴当OP>3时,点P一定在⊙O的外部.
故答案为:>3.
【点睛】本题考查了点与圆的位置关系,根据点的位置可以确定该点到圆心距离与半径的关系.
【变式7-2】(23-24九年级·江苏南通·期中)在数轴上,点A所表示的实数为4,点B所表示的实数为b,的半径为2,要使点B在内时,实数b的取值范围是( )
A. B. C.或 D.
【答案】D
【分析】要使点B在内,则,即,求解即可.
【详解】解:要使点B在内,则,即
解得,
故选:D
【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
【变式7-3】(23-24九年级·上海·专题练习)如图,在中,,,,点在边上,,的半径长为,与相交,且点在外,那么的半径长可能是( )
A. B. C. D.
【答案】B
【分析】连接交于,根据勾股定理求出的长,从而求出的长,再根据相交两圆的位置关系得出的范围即可.
【详解】解:连接交于,如图,
在 中,由勾股定理得:,
则,
,
,
与相交,且点在外,必须,
即只有选项B符合题意,
故选:B.
【点睛】本题考查了相交两圆的性质,点与圆的位置关系,勾股定理等知识点,能熟记相交两圆的性质和点与圆的位置关系的内容是解题的关键.
【题型8 求一点到圆上点的距离的最值】
【例8】(23-24·陕西·模拟预测)如图,在矩形中,,, 是平面内一动点,且,则线段的最大值为 .
【答案】/
【分析】该题主要考查了矩形的性质,勾股定理,圆相关知识点,解题的关键是明确点的运动轨迹.
根据勾股定理算出,再根据题意确定点在以为半径的上运动,的最大值,即可求解;
【详解】解:∵四边形是矩形,
∴,
∴,
∵,
∴点在以为半径的上运动,
如图当三点共线时,
最大,最大值.
故答案为:.
【变式8-1】(23-24·河南郑州·三模)如图,点M是等边三角形边的中点,P是三角形内一点,连接,将线段以A为中心逆时针旋转得到线段,连接.若,,则的最小值为 .
【答案】
【分析】本题考查旋转的性质、等边三角形的判定与性质、勾股定理、全等三角形的判定与性质、圆的有关定义以及和性质等知识,得到点Q的运动路线是解答的关键.连接,,将线段绕着点A逆时针旋转得到线段,连接,,由旋转性质可推导,是等边三角形,则,,根据圆的定义可得点Q在以H为圆心,1为半径的圆上运动,进而可知当M、Q、H共线时,最小,最小值为,根据等边三角形的性质求得值即可求解.
【详解】解:连接,,将线段绕着点A逆时针旋转得到线段,连接,,
由旋转性质得,,,即,
∴,是等边三角形,
∴,,
则点Q在以H为圆心,1为半径的圆上运动,
∵,
∴当M、Q、H共线时,最小,最小值为,
∵点M是等边三角形边的中点,,
∴,,
∴,即,
∴的最小值为,
故答案为:.
【变式8-2】(23-24九年级·湖北武汉·期中)如图,已知在中,,,将绕点A逆时针旋转.得到.点D是边的中点,点E为边上的动点,在绕点A逆时针旋转的过程中,点E的对应点是点,则线段长度的最大值与最小值的差是 .
【答案】
【分析】如图,连接,作于H,于.求出的最小值以及最大值即可解决问题.
【详解】解:如图,连接,作于H,于.
以A为圆心,以为半径作圆,与直线的右侧交点为,
以A为圆心,以为半径作圆,与直线的左侧交点为,
∵,,点D是边的中点,
∴,,
∴,
∵,
∴,
在旋转过程中,当点与重合时,的值最小,且最小值为:,
当点与重合时,的值最大,且最大值,
∴线段长度的最大值与最小值的差为:,
故答案为:.
【点睛】本题考查了旋转的性质,勾股定理,等腰三角形的三线合一性质,垂线段最短,圆的基本性质,熟练掌握勾股定理,等腰三角形的三线合一性质,垂线段最短,圆的基本性质是解题的关键.
【变式8-3】(23-24九年级·江苏镇江·阶段练习)如图,正比例函数与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的上运动,点Q是的中点,则长的最大值为( )
A. B. C. D.
【答案】A
【分析】本题考查了正比例函数与反比例函数的交点问题,三角形中位线定理,圆的性质等知识点,熟练掌握正比例函数与反比例函数的性质是解题关键.连结,根据反比例函数的中心对称性可得,即得是的中位线,所以,当经过圆心C时,取得最大值,最大值为,求出,的值,即得答案.
【详解】连结,
正比例函数与反比例函数的图象交于A、B两点,
点A与点B关于原点O对称,
,
点Q是AP的中点,
是的中位线,
,
当经过圆心C时,取得最大值,最大值为,
联立,
解得或,
,
,
,
点P在1为半径的上运动,
,
,
长的最大值为.
故选A.
【题型9 圆中角度的计算】
【例9】(23-24九年级·广东珠海·期末)如图,在平面直角坐标系中,B,C为x轴上两点,以点O为圆心画圆(直径小于),交y轴负半轴于点A,过点A作x轴平行线,点P为圆上一个动点,连接,下列说法正确的有( )
①当点P运动到第一象限,则
②当点P运动到第二象限,则
③当点P运动到第三象限,则
④当点P运动到第四象限,则
A.①② B.③④ C.①④ D.②③
【答案】D
【分析】本题考查了等腰三角形的判定及性质,平行线的性质,解题的关键是利用数形结合的思想来求解,画出每一种情况的图形,然后利用平行线的性质求解.
【详解】解:①当点P运动到第一象限,则,故①错误;
②当点P运动到第二象限,
则,故②正确;
③当点P运动到第三象限,
则,故③正确;
④当点P运动到第四象限,则,
则,故④错误,
故正确的为:②③,
故选:D.
【变式9-1】(23-24九年级·江苏连云港·阶段练习)如图,的圆心为点,以点为圆心作,且与的延长线交于点,与的延长线交于点.已知,求的度数.
【答案】
【分析】由等腰三角形的性质及三角形的内角和定理得 ,再由等腰三角形的性质及三角形外角性质得 ,继而利用三角形的外角性质即可得解.
【详解】解:∵,,
∴ ,
∵,
∴,
∵,
∴ ,
∴ ,
∵,
∴
【点睛】本题主要考查了等腰三角形的性质、三角形的内角和定理及外角性质以及圆的认识,熟练掌握三角形的内角和定理及等腰三角形的性质是解题的关键.
【变式9-2】(23-24九年级·湖南湘西·期中)如图,是半圆的直径,点是半圆上不与点、重合的一个动点,延长到点,使,是的中点,连接、.
(1)求证: ;
(2)连接,当四边形是菱形时,求的度数.
【答案】(1)见解析
(2)
【分析】(1)根据中位线的性质得到, ,由可证;
(2)根据菱形的性质得,从而证是等边三角形,利用等边三角形的性质即可求解.
【详解】(1)解:点是的中点,,
,,
.
,
,
在和中,
,
;
(2)解:连接,
四边形是菱形,
∴,
∵,
∴,
∴是等边三角形,
.
【点睛】本题主要考查全等三角形的判定与性质、等边三角形的判定及性质以及菱形的性质,解题关键是根据中位线的性质得到, ,由得出.
【变式9-3】(23-24·湖北武汉·一模)如图,在中,,C为上一点,连接.
(1)若,求的度数;
(2)若的面积与的面积之比为,求的值.
【答案】(1)∠BOC的度数为50°
(2)
【分析】(1)设,先根据等边对等角和三角形内角和定理得到,再根据建立方程求解即可;
(2)过C作于H,设,根据三角形面积之比求出,则由勾股定理得,进而得到,再利用勾股定理求出的长即可得到答案.
【详解】(1)解:设,
∵,
∴,
∵,
∴,
解得,
∴;
(2)
解:过C作于H,设,
∵的面积与的面积之比为,
∴,
∴,
∴,
∴,
∴,
在中,由勾股可得,
在中,由勾股可得,
∴.
【点睛】本题主要考查了圆的基本性质,勾股定理,等边对等角,三角形内角和定理,正确作出辅助线构造直角三角形是解题的关键.
【题型10 圆中线段长度的计算】
【例10】(23-24·上海虹口·二模)如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A的对称点),那么的长为 .
【答案】/
【分析】本题考查翻折性质,圆的基本性质,等边三角形判定与性质、勾股定理的应用,连接,由翻折得,证出是等边三角形,设,在中,根据勾股定理列方程并解出进而求出结论.
【详解】解:连接,
由翻折得:,,
,
是等边三角形,
,
,
设,则,
在中,,
,
解得:(舍去),
,
故答案为:.
【变式10-1】(23-24九年级·山东滨州·期中)如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D,若点D巧好为线段AB的中点,则AB的长度为( )
A. B.3 C. 6 D.9
【答案】C
【分析】根据直角三角形斜边上的中线的圆的性质求解即可;
【详解】连接CD,
∵以点C为圆心、CA为半径的圆与AB交于点D,AC=3,
∴,
又∵在Rt△ABC中,∠ACB=90°,D为线段AB的中点,
∴,
∴;
故选C.
【点睛】本题主要考查了直角三角形斜边上的中线是斜边的一半和圆的性质,准确计算是解题的关键.
【变式10-2】(23-24九年级·浙江绍兴·期末)如图,正方形的边长为4,点在边上,,点在上,与直线交于点(点在点右侧),则的长度为( )
A. B.8 C. D.
【答案】C
【分析】连接,由正方形性质可得,,,然后用勾股定理求出半径,再求出的长即可.
【详解】解:连接,
∵正方形的边长为4,,
∴,,,
∴在中,,
∴,
∴,
∴在中,,
故选:C.
【点睛】本题考查正方形的性质、圆的性质及勾股定理等知识,解题的关键是熟练掌握有关圆的性质,属于中考常考题型.
【变式10-3】(23-24·广东江门·模拟预测)综合探究
如图,在扇形中,是上异于的动点,过点作于点,作于点,连接,点在线段上,且.
(1)求证:四边形是平行四边形.
(2)当点在上运动时,在中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.
(3)求证:是定值.
【答案】(1)见解析;
(2)存在,1;
(3)见解析.
【分析】本题主要考查圆的基本性质以及勾股定理:
(1)道德证明四边形是矩形,得,同理可证,得出四边形是平行四边形.
(2)根据点A是上的点,,得出,由得出;
(3)过点作于点.设,则,求出,,计算出,进一步可得出结论
【详解】(1)证明:如图,连接交于点.
,
,
四边形是矩形,
.
,
,
,
四边形是平行四边形.
(2)解:存在,线段的长度不变.
∵点A是上的点,
在矩形中,.
,
.
(3)解:如图,过点作于点.
设,则.
由,得,
.
,
,
,
是定值.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 圆的基本概念】 1
【题型2 识别圆心角】 2
【题型3 求圆中弦的条数】 3
【题型4 圆的周长和面积】 4
【题型5 确定圆内一点最长的弦】 5
【题型6 判断点与圆的位置关系】 6
【题型7 由点与圆的位置关系求半径】 7
【题型8 求一点到圆上点的距离的最值】 8
【题型9 圆中角度的计算】 9
【题型10 圆中线段长度的计算】 10
知识点1:圆的有关概念
圆的定义:第一种:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫作圆。固定的端点O叫作圆心,线段OA叫作半径。
第二种:圆心为O,半径为r的圆可以瞧成就是所有到定点O的距离等于定长r的点的集合。
比较圆的两种定义可知:第一种定义就是圆的形成进行描述的,第二种就是运用集合的观点下的定义,但就是都说明确定了定点与定长,也就确定了圆。
弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫作直径。
弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。小于半圆的弧叫做劣弧。大于半圆的弧叫做优弧。
等圆:等够重合的两个圆叫做等圆。
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
弦就是线段,弧就是曲线,判断等弧首要的条件就是在同圆或等圆中,只有在同圆或等圆中完全重合的弧才就是等弧,而不就是长度相等的弧。
同圆或等圆的半径相等.
【题型1 圆的基本概念】
【例1】(23-24九年级·山东潍坊·期末)下列说法正确的有( )
A.经过圆心的线段是直径 B.直径是同一个圆中最长的弦
C.长度相等的两条弧是等弧 D.弧分为优弧和劣弧
【变式1-1】(23-24·甘肃平凉·模拟预测)如图, 的两条弦、的延长线交于C点,的平分线过点O,请直接写出图中一对相等的线段: .
【变式1-2】(23-24·湖南常德·一模)如图,在平面直角坐标系中,点A的坐标为,点B在y轴正半轴上,以点B为圆心,长为半径作弧,交x轴正半轴于点C,则点C的坐标为 .
【变式1-3】(23-24·河北邯郸·二模)如图,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
知识点2:圆心角
顶点在圆心的角叫圆心角.
【题型2 识别圆心角】
【例2】(23-24·山东烟台·中考真题)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接,则的度数为 .
【变式2-1】(23-24九年级·全国·课后作业)下图中是圆心角的是( )
A. B. C. D.
【变式2-2】(23-24九年级·江苏南京·期中)在中,弦的长恰好等于半径,弦所对的圆心角为 .
【变式2-3】(23-24九年级·江苏镇江·阶段练习)如图,、是⊙O的直径,弦,弧的度数为,求的度数.
【题型3 求圆中弦的条数】
【例3】(23-24九年级·河南濮阳·期末)如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
【变式3-1】(23-24九年级·江西南昌·阶段练习)如图,是内接三角形,请仅用无刻度的直尺,分别按下列要求画图.
(1)在图1中,画山一条与相等的弦;
(2)在图2中,画出一个与全等的三角形.
【变式3-2】(23-24九年级·河南·课后作业)如图,圆中有 条直径, 条弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
【变式3-3】(23-24九年级·全国·课后作业)的半径为,A为上一定点,点P在上沿圆周运动(不与点A重合),则使弦的长度为整数的点P共有 个.
【题型4 圆的周长和面积】
【例4】(23-24九年级·山东潍坊·期末)由所有到已知点O的距离不小于3,并且不大于5的点组成的图形的面积为 .
【变式4-1】(23-24九年级·上海静安·期末)如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
【变式4-2】(23-24九年级·福建厦门·期末)如图,长方形ABCD的面积为225,长和宽的比为5∶3,在此长方形内沿着边的方向能否并排裁出两个面积均为的圆(取3),请通过计算说明理由.
【变式4-3】(23-24九年级·湖北武汉·期末)如图,是编号为1、2、3、4的400m跑道,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每条跑道宽1m,内侧的1号跑道长度为400m,则2号跑道比1号跑道长 m;若在一次200m比赛中(每个跑道都由一个半圆形跑道和部分直跑道组成),要使得每个运动员到达同一终点线,则4号跑道起跑点比2号跑道起跑点应前移 m(π取3.14).
【题型5 确定圆内一点最长的弦】
【例5】(23-24·广东深圳·二模)如图(a),A,B是⊙O上两定点,,圆上一动点P从点B出发,沿逆时针方向匀速运动到点A,运动时间是,线段AP的长度是.图(b)是y随x变化的关系图象,其中图象与x轴交点的横坐标记为m,则m的值是( )
A.8 B.6 C. D.
【变式5-1】(23-24九年级·河南周口·期末)若的直径长为,点,在上,则的长不可能是( )
A.2 B.3 C.4 D.5
【变式5-2】(23-24九年级·浙江杭州·阶段练习)如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
【变式5-3】(23-24九年级·江苏宿迁·期中)如图,的半径为5,弦的长为6,延长至点,使得点为的中点,在上任取一点,连接、,则的最大值为( )
A.290 B.272 C.252 D.244
知识点3:点与圆的位置关系
设⊙O的半径为r,点P到圆心的距离为OP=d,则有:
点P在圆外d>r;
点P在圆上d=r;
点P在圆内d<r.
【题型6 判断点与圆的位置关系】
【例6】(23-24九年级·安徽阜阳·期末)在平面内,的半径为,点到圆心的距离为,则点与的位置关系是点在 .(填“圆内”“圆外”或“圆上”).
【变式6-1】(23-24九年级·广东湛江·期末)如图,在中,,点D在边上,且,以为直径作,设线段的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
【变式6-2】(23-24九年级·北京海淀·期末)如图,,,是某社区的三栋楼,若在中点处建一个基站,其覆盖半径为200m,则这三栋楼中在该基站覆盖范围内的是( )
A.,,都不在 B.只有 C.只有, D.,,
【变式6-3】(23-24九年级·浙江宁波·期末)如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
【题型7 由点与圆的位置关系求半径】
【例7】(23-24九年级·北京顺义·期末)已知矩形中, ,,以点B为圆心r为半径作圆,且与边有唯一公共点,则r的取值范围是 .
【变式7-1】(23-24九年级·山东烟台·期末)点P是⊙O所在平面内一点,若⊙O的面积为,则当OP 时,点P-定在⊙O的外部.
【变式7-2】(23-24九年级·江苏南通·期中)在数轴上,点A所表示的实数为4,点B所表示的实数为b,的半径为2,要使点B在内时,实数b的取值范围是( )
A. B. C.或 D.
【变式7-3】(23-24九年级·上海·专题练习)如图,在中,,,,点在边上,,的半径长为,与相交,且点在外,那么的半径长可能是( )
A. B. C. D.
【题型8 求一点到圆上点的距离的最值】
【例8】(23-24·陕西·模拟预测)如图,在矩形中,,, 是平面内一动点,且,则线段的最大值为 .
【变式8-1】(23-24·河南郑州·三模)如图,点M是等边三角形边的中点,P是三角形内一点,连接,将线段以A为中心逆时针旋转得到线段,连接.若,,则的最小值为 .
【变式8-2】(23-24九年级·湖北武汉·期中)如图,已知在中,,,将绕点A逆时针旋转.得到.点D是边的中点,点E为边上的动点,在绕点A逆时针旋转的过程中,点E的对应点是点,则线段长度的最大值与最小值的差是 .
【变式8-3】(23-24九年级·江苏镇江·阶段练习)如图,正比例函数与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的上运动,点Q是的中点,则长的最大值为( )
A. B. C. D.
【题型9 圆中角度的计算】
【例9】(23-24九年级·广东珠海·期末)如图,在平面直角坐标系中,B,C为x轴上两点,以点O为圆心画圆(直径小于),交y轴负半轴于点A,过点A作x轴平行线,点P为圆上一个动点,连接,下列说法正确的有( )
①当点P运动到第一象限,则
②当点P运动到第二象限,则
③当点P运动到第三象限,则
④当点P运动到第四象限,则
A.①② B.③④ C.①④ D.②③
【变式9-1】(23-24九年级·江苏连云港·阶段练习)如图,的圆心为点,以点为圆心作,且与的延长线交于点,与的延长线交于点.已知,求的度数.
【变式9-2】(23-24九年级·湖南湘西·期中)如图,是半圆的直径,点是半圆上不与点、重合的一个动点,延长到点,使,是的中点,连接、.
(1)求证: ;
(2)连接,当四边形是菱形时,求的度数.
【变式9-3】(23-24·湖北武汉·一模)如图,在中,,C为上一点,连接.
(1)若,求的度数;
(2)若的面积与的面积之比为,求的值.
【题型10 圆中线段长度的计算】
【例10】(23-24·上海虹口·二模)如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A的对称点),那么的长为 .
【变式10-1】(23-24九年级·山东滨州·期中)如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D,若点D巧好为线段AB的中点,则AB的长度为( )
A. B.3 C. 6 D.9
【变式10-2】(23-24九年级·浙江绍兴·期末)如图,正方形的边长为4,点在边上,,点在上,与直线交于点(点在点右侧),则的长度为( )
A. B.8 C. D.
【变式10-3】(23-24·广东江门·模拟预测)综合探究
如图,在扇形中,是上异于的动点,过点作于点,作于点,连接,点在线段上,且.
(1)求证:四边形是平行四边形.
(2)当点在上运动时,在中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.
(3)求证:是定值.21世纪教育网(www.21cnjy.com)
专题24.1 圆【十大题型】
【人教版】
【题型1 圆的基本概念】 1
【题型2 识别圆心角】 4
【题型3 求圆中弦的条数】 7
【题型4 圆的周长和面积】 10
【题型5 确定圆内一点最长的弦】 13
【题型6 判断点与圆的位置关系】 16
【题型7 由点与圆的位置关系求半径】 20
【题型8 求一点到圆上点的距离的最值】 22
【题型9 圆中角度的计算】 27
【题型10 圆中线段长度的计算】 32
知识点1:圆的有关概念
圆的定义:第一种:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫作圆。固定的端点O叫作圆心,线段OA叫作半径。
第二种:圆心为O,半径为r的圆可以瞧成就是所有到定点O的距离等于定长r的点的集合。
比较圆的两种定义可知:第一种定义就是圆的形成进行描述的,第二种就是运用集合的观点下的定义,但就是都说明确定了定点与定长,也就确定了圆。
弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫作直径。
弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。小于半圆的弧叫做劣弧。大于半圆的弧叫做优弧。
等圆:等够重合的两个圆叫做等圆。
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
弦就是线段,弧就是曲线,判断等弧首要的条件就是在同圆或等圆中,只有在同圆或等圆中完全重合的弧才就是等弧,而不就是长度相等的弧。
同圆或等圆的半径相等.
【题型1 圆的基本概念】
【例1】(23-24九年级·山东潍坊·期末)下列说法正确的有( )
A.经过圆心的线段是直径 B.直径是同一个圆中最长的弦
C.长度相等的两条弧是等弧 D.弧分为优弧和劣弧
【答案】B
【分析】本题考查了圆的相关概念,解题的关键是掌握直径的定义,弧的定义,弧的分类,根据相关概念,逐个判断即可.
【详解】解:A、经过圆心,且两端点在圆上的线段是直径,故A不正确,不符合题意;
B、直径是同一个圆中最长的弦,故B正确,符合题意;
C、在同圆或等圆中,长度相等的两条弧是等弧,故C不正确,不符合题意;
D、弧分为优弧、劣弧和半圆,故D不正确,不符合题意;
故选:B.
【变式1-1】(23-24·甘肃平凉·模拟预测)如图, 的两条弦、的延长线交于C点,的平分线过点O,请直接写出图中一对相等的线段: .
【答案】(或或)
【分析】根据圆是轴对称图形,对称轴是经过圆心的每一条直线;角是轴对称图形,对称轴是角平分线所在的直线结合进行判断.此题关键是根据图形的对称性,分析可以重合的线段.
【详解】这个图形是轴对称图形,对称轴即是直线,根据轴对称的性质,得或或.
故答案为:(或或).
【变式1-2】(23-24·湖南常德·一模)如图,在平面直角坐标系中,点A的坐标为,点B在y轴正半轴上,以点B为圆心,长为半径作弧,交x轴正半轴于点C,则点C的坐标为 .
【答案】
【分析】本题考查了同圆半径相等、等腰三角形的三线合一、点坐标等知识点.连接,先根据点的坐标可得,再根据等腰三角形的判定可得是等腰三角形,然后根据等腰三角形的三线合一可得,由此即可得出答案.
【详解】解:如图,连接,
点的坐标为,
,
由同圆半径相等得:,
是等腰三角形,
,
(等腰三角形的三线合一),
又点位于轴正半轴,
点的坐标为,
故答案为:.
【变式1-3】(23-24·河北邯郸·二模)如图,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
【答案】D
【分析】本题主要考查圆的性质和平行四边形的判定,在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,可得,故可判断四边形是平行四边形
【详解】解:在两个同心圆中,分别是大圆和小圆的直径,且与不在同一条直线上,
∴,
∴四边形是平行四边形
故选:D
知识点2:圆心角
顶点在圆心的角叫圆心角.
【题型2 识别圆心角】
【例2】(23-24·山东烟台·中考真题)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接,则的度数为 .
【答案】
【分析】方法一∶如图:连接,由题意可得:,,然后再根据等腰三角形的性质求得、,最后根据角的和差即可解答.
方法二∶ 连接,由题意可得:,然后根据圆周角定理即可求解.
【详解】方法一∶ 解:如图:连接,
由题意可得:,,,
∴,,
∴.
故答案为.
方法二∶解∶ 连接,
由题意可得:,
根据圆周角定理,知.
故答案为.
【点睛】本题主要考查了角的度量、圆周角定理等知识点,掌握圆周角的度数等于它所对弧上的圆心角度数的一半是解答本题的关键.
【变式2-1】(23-24九年级·全国·课后作业)下图中是圆心角的是( )
A. B. C. D.
【答案】C
【分析】根据圆心角的概念:圆心角是指在中心为O的圆中,过弧AB两端的半径构成的∠AOB, 称为弧AB所对的圆心角进行判断.
【详解】解:A、不是圆心角,故不符合题意;
B、不是圆心角,故不符合题意;
C、是圆心角,故符合题意;
D、不是圆心角,故不符合题意;
故选:C.
【点睛】本题考查的是圆心角的概念,掌握顶点在圆心的角叫作圆心角是解题的关键.
【变式2-2】(23-24九年级·江苏南京·期中)在中,弦的长恰好等于半径,弦所对的圆心角为 .
【答案】60
【分析】本题考查了圆心角、等边三角形的判定与性质,熟练掌握圆心角是解题关键.根据等边三角形的判定与性质可得,由此即可得.
【详解】解:如图,∵在中,弦的长恰好等于半径,
,
是等边三角形,
,
即弦所对的圆心角为,
故答案为:60.
【变式2-3】(23-24九年级·江苏镇江·阶段练习)如图,、是⊙O的直径,弦,弧的度数为,求的度数.
【答案】
【分析】连接,由弧的度数为,得到,根据等腰三角形的性质和三角形的内角和定理可求出,再由,即可得到.
【详解】解:连接,如图,
∵弧的度数为,
∴,
∵,
∴,
∴,
∵弦,
∴.
【点睛】本题考查了圆的基本性质,等腰三角形的性质,三角形内角和定理以及平行线的性质,熟练掌握圆的基本性质是解题的关键.
【题型3 求圆中弦的条数】
【例3】(23-24九年级·河南濮阳·期末)如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
【答案】B
【分析】根据弦的定义进行分析,从而得到答案.
【详解】解:图中的弦有AB,BC,CE共三条,
故选B.
【点睛】本题主要考查了弦的定义,熟知定义是解题的关键:连接圆上任意两点的线段叫弦.
【变式3-1】(23-24九年级·江西南昌·阶段练习)如图,是内接三角形,请仅用无刻度的直尺,分别按下列要求画图.
(1)在图1中,画山一条与相等的弦;
(2)在图2中,画出一个与全等的三角形.
【答案】(1)见解析;(2)见解析
【分析】(1)连结CO并延长交于E,连接BO并延长交于D,连结ED,再证△BOC≌△DOE(SAS),可得BC=DE;
(2)连结AO并延长交于A′,OA=OA′,连结BO并延长交于B′,OB=OB′,连结CO并延长交于C′,OC=OC′,利用边角边判定方法先证△BOC≌△B′OC′(SAS),可得BC=B′C′;同理可证△BOA≌△B′OA′(SAS),可得AB=A′B′,同理可证△AOC≌△A′OC′(SAS),可得AC=A′C′,利用三边对应相等判定方法可证△ABC≌△A′B′C′(SSS).
【详解】解:(1)如图1,DE为所作;
连结CO并延长交于E,连接BO并延长交于D,连结ED,
∵OB=OD=OE=OC,
在△BOC和△DOE中,
,
∴△BOC≌△DOE(SAS),
∴BC=DE;
(2)如图2,△A′B′C′为所作.
连结AO并延长交于A′,OA=OA′,连结BO并延长交于B′,OB=OB′,连结CO并延长交于C′,OC=OC′,
在△BOC和△B′OC′中,
,
∴△BOC≌△B′OC′(SAS),
∴BC=B′C′;
同理可证△BOA≌△B′OA′(SAS),
∴AB=A′B′,
同理可证△AOC≌△A′OC′(SAS),
∴AC=A′C′,
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(SSS).
【点睛】本题考查仅用无刻度的直尺画线段,画三角形,三角形全等判定与性质,圆的性质,掌握圆的性质与三角形全等判定与性质是解题关键.
【变式3-2】(23-24九年级·河南·课后作业)如图,圆中有 条直径, 条弦,圆中以A为一个端点的优弧有 条,劣弧有 条.
【答案】 1 3 4 4
【详解】圆中有AB一条直径,AB、CD、EF三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条,
故答案为1,3,4,4.
【变式3-3】(23-24九年级·全国·课后作业)的半径为,A为上一定点,点P在上沿圆周运动(不与点A重合),则使弦的长度为整数的点P共有 个.
【答案】7
【分析】本题主要考查了圆的弦的概念.熟练掌握圆的弦的定义和性质,是解决问题的关键.圆的弦的定义:连接圆上任意两点间的线段叫做弦.最大弦是直径.
根据的半径为,得到直径,根据,得到在半圆上,有3个,另一侧也有3个,加上长度为的是与B点重合,一共有7个.
【详解】如图,∵的半径为,
∴直径,
∴弦长的整数值有或或或,共4种可能,
当或或时,各有2条,
当时有1条,
∴这样的弦共有7条.
∴这样的点P共有7个.
故答案为:7.
【题型4 圆的周长和面积】
【例4】(23-24九年级·山东潍坊·期末)由所有到已知点O的距离不小于3,并且不大于5的点组成的图形的面积为 .
【答案】
【分析】根据题意调查到点的距离不小于3,并且不大于5的点组成的图形是半径为5和半径为所组成的环形面积即可.本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
【详解】解:如图,
到点的距离不小于3,并且不大于5的点组成的图形是图中环形,
所以
.
故答案为:.
【变式4-1】(23-24九年级·上海静安·期末)如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
【答案】
【分析】设小圆的半径为r,则大圆的半径为,根据,列方程求得大圆和小圆的半径,再计算大圆和小圆的周长之和即可求解.
【详解】解:设小圆的半径为r,则大圆的半径为,
由图可得,,即,
解得, (舍),,
∴,
∴,
答:围成圆环铁丝的总长度为.
【变式4-2】(23-24九年级·福建厦门·期末)如图,长方形ABCD的面积为225,长和宽的比为5∶3,在此长方形内沿着边的方向能否并排裁出两个面积均为的圆(取3),请通过计算说明理由.
【答案】不能并排裁出两个面积均为75cm2的圆,理由见解析
【分析】根据长方形的长宽比设长方形的长AB为5x cm,宽AD为3x cm,结合长方形ABCD的面积为225,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积为,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
【详解】解:设长方形的长AB为5x cm,宽AD为3x cm,
根据题意得,
解得(负值舍弃),
∴,
∴,,
∵圆的面积为75,设圆的半径为rcm,
∴,
解得,
∴,
∵,
∴不能并排裁出两个面积均为75cm2的圆.
【点睛】本题考查了解一元二次方程、圆的面积以及实数大小的比较,解题关键是求出圆的半径以及长方形的长.
【变式4-3】(23-24九年级·湖北武汉·期末)如图,是编号为1、2、3、4的400m跑道,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每条跑道宽1m,内侧的1号跑道长度为400m,则2号跑道比1号跑道长 m;若在一次200m比赛中(每个跑道都由一个半圆形跑道和部分直跑道组成),要使得每个运动员到达同一终点线,则4号跑道起跑点比2号跑道起跑点应前移 m(π取3.14).
【答案】 6.28 6.28
【分析】利用各跑道直线跑道相等,每条跑道宽1m,两个半圆相加得一个整圆列出式子对比即可.
【详解】解:设直线部分长为l米
1号:
2号:
3号:
4号:
2号比1号长:
4号起点比2号起点前移:
故答案为:6.28,6.28
【点睛】本题考查了列代数式,圆的周长公式,整式的加减等知识点,熟练掌握是解题的关键.
【题型5 确定圆内一点最长的弦】
【例5】(23-24·广东深圳·二模)如图(a),A,B是⊙O上两定点,,圆上一动点P从点B出发,沿逆时针方向匀速运动到点A,运动时间是,线段AP的长度是.图(b)是y随x变化的关系图象,其中图象与x轴交点的横坐标记为m,则m的值是( )
A.8 B.6 C. D.
【答案】B
【分析】本题考查了动点问题的函数图形,合理分析动点的运动时间是解题关键.
根据最长时经过的路程所用的运动时间,求出总路程所用的时间是之前的三倍,即可解答.
【详解】解:如图,当点运动到过圆心,即为直径时,最长,
由图(b)得,最长时为6,此时,
,
,
此时点路程为90度的弧,
点从点运动到点的弧度为270度,
运动时间为,
故选:B.
【变式5-1】(23-24九年级·河南周口·期末)若的直径长为,点,在上,则的长不可能是( )
A.2 B.3 C.4 D.5
【答案】D
【分析】根据直径是最长的弦即可求解.
【详解】解:∵若的直径长为,点,在上,
∴的长不可能是,
故选:D.
【点睛】本题考查了圆的相关概念,掌握直径是最长的弦是解题的关键.
【变式5-2】(23-24九年级·浙江杭州·阶段练习)如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
【答案】2
【分析】如图,连接并延长,交圆于点D,连接,由中位线定理,得,点A为定点,C为动点,的最大值为直径长,即长.于是的最大值为.
【详解】解:如图,连接并延长,交圆于点D,连接,
∵点M,N分别是AB,BC中点,
∴.
点A为定点,C为动点,的最大值为直径长,即长.
∵是直径,
∴.
∴的最大值为.
故答案为:2
【点睛】本题考查中位线定理,圆的基本概念弦与直径;掌握中位线定理是解题的关键.
【变式5-3】(23-24九年级·江苏宿迁·期中)如图,的半径为5,弦的长为6,延长至点,使得点为的中点,在上任取一点,连接、,则的最大值为( )
A.290 B.272 C.252 D.244
【答案】B
【分析】本题考查了勾股定理,圆内最长弦是直径,过点C作于点N,连接,根据勾股定理可得 ,,利用弦最长等于直径即可得出答案.
【详解】解:过点C作于点N,连接,
点为的中点,,
,
,
,
,
,
当最大时,最大,
在中,
,
当最大时,最大,
的半径为5,
弦最长等于直径是10,
,
.
故选:B.
知识点3:点与圆的位置关系
设⊙O的半径为r,点P到圆心的距离为OP=d,则有:
点P在圆外d>r;
点P在圆上d=r;
点P在圆内d<r.
【题型6 判断点与圆的位置关系】
【例6】(23-24九年级·安徽阜阳·期末)在平面内,的半径为,点到圆心的距离为,则点与的位置关系是点在 .(填“圆内”“圆外”或“圆上”).
【答案】圆外
【分析】本题考查了点与圆的位置关系,设的半径为,点到圆心的距离,则有:点在圆外;点在圆上;点在圆内;据此即可判断求解,掌握点与圆的位置关系是解题的关键.
【详解】解:∵的半径为,点到圆心的距离为,
∴,
∴点在圆外,
故答案为:圆外.
【变式6-1】(23-24九年级·广东湛江·期末)如图,在中,,点D在边上,且,以为直径作,设线段的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
【答案】C
【分析】本题考查了对点与圆的位置关系的判断,三角形中位线定理等知识.关键要记住若半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.首先根据三角形中位线的性质得出,进而利用点与圆的位置关系得出即可.
【详解】解:连接,
∵以为直径作,线段的中点为P,
∴是的中位线,
∴,
∵,
∴,
∴点P与的位置关系是点P在外.
故选:C.
【变式6-2】(23-24九年级·北京海淀·期末)如图,,,是某社区的三栋楼,若在中点处建一个基站,其覆盖半径为200m,则这三栋楼中在该基站覆盖范围内的是( )
A.,,都不在 B.只有 C.只有, D.,,
【答案】A
【分析】
根据勾股定理的逆定理证得是直角三角形,可以根据直角三角形斜边中线的性质求得的长,然后与比较大小,即可解答本题.本题考查勾股定理的逆定理,直角三角形斜边上的中线的性质,点D与圆的位置关系,解题的关键是求出三角形三个顶点到点的距离.
【详解】
解:,,,
,
是直角三角形,且,
点是斜边的中点,
,,
如图,以为圆心,为半径画圆,
,
点A,B,C都不在覆盖范围内,
故选:A.
【变式6-3】(23-24九年级·浙江宁波·期末)如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
【答案】A
【分析】根据等腰三角形的性质求出BD=CD=6cm,利用勾股定理求出AD,得到AP的长,即可判断点A与的位置关系;利用勾股定理求出BP、CP,即可判断点B、C与的位置关系,由DP即可判断点D与位置关系.
【详解】解:∵,
∴BD=CD=6cm,∠ADC=90°,
∴cm,
∵DP=2cm,
∴AP=6cm,
∴点A在上;故A选项符合题意;
连接BP、CP,
∵,
∴AD垂直平分BC,
∴BP=CP=,
∴点B、C都在外;故B、C选项都不符合题意;
∵DP=2<6,
∴点在内,故D选项不符合题意,
故选:A.
【点睛】此题考查了点与圆的位置关系,勾股定理,线段垂直平分线的判定及性质,等腰三角形三线合一的性质,熟记点与圆的位置关系是解题的关键.
【题型7 由点与圆的位置关系求半径】
【例7】(23-24九年级·北京顺义·期末)已知矩形中, ,,以点B为圆心r为半径作圆,且与边有唯一公共点,则r的取值范围是 .
【答案】
【分析】连接,,利用勾股定理求出的长,抓住已知以点B为圆心r为半径作圆,且与边有唯一公共点,就可求出的半径r的取值范围.
【详解】解:连接,,
∵矩形中,,,
∴,,,
∵以点B为圆心作圆,与边有唯一公共点,
∴的半径r的取值范围是:;
故答案为:.
【点睛】此题考查了点与圆的位置关系以及矩形的性质,勾股定理.注意若半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.
【变式7-1】(23-24九年级·山东烟台·期末)点P是⊙O所在平面内一点,若⊙O的面积为,则当OP 时,点P-定在⊙O的外部.
【答案】>3
【分析】由⊙O的面积为9π,可求出半径为3,再根据点P在圆外d>r可得解.
【详解】解:设⊙O的半径为r,
∵⊙O的面积为9π,
∴,
∴r=3,
∴⊙O的半径为3,
∴当OP>3时,点P一定在⊙O的外部.
故答案为:>3.
【点睛】本题考查了点与圆的位置关系,根据点的位置可以确定该点到圆心距离与半径的关系.
【变式7-2】(23-24九年级·江苏南通·期中)在数轴上,点A所表示的实数为4,点B所表示的实数为b,的半径为2,要使点B在内时,实数b的取值范围是( )
A. B. C.或 D.
【答案】D
【分析】要使点B在内,则,即,求解即可.
【详解】解:要使点B在内,则,即
解得,
故选:D
【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
【变式7-3】(23-24九年级·上海·专题练习)如图,在中,,,,点在边上,,的半径长为,与相交,且点在外,那么的半径长可能是( )
A. B. C. D.
【答案】B
【分析】连接交于,根据勾股定理求出的长,从而求出的长,再根据相交两圆的位置关系得出的范围即可.
【详解】解:连接交于,如图,
在 中,由勾股定理得:,
则,
,
,
与相交,且点在外,必须,
即只有选项B符合题意,
故选:B.
【点睛】本题考查了相交两圆的性质,点与圆的位置关系,勾股定理等知识点,能熟记相交两圆的性质和点与圆的位置关系的内容是解题的关键.
【题型8 求一点到圆上点的距离的最值】
【例8】(23-24·陕西·模拟预测)如图,在矩形中,,, 是平面内一动点,且,则线段的最大值为 .
【答案】/
【分析】该题主要考查了矩形的性质,勾股定理,圆相关知识点,解题的关键是明确点的运动轨迹.
根据勾股定理算出,再根据题意确定点在以为半径的上运动,的最大值,即可求解;
【详解】解:∵四边形是矩形,
∴,
∴,
∵,
∴点在以为半径的上运动,
如图当三点共线时,
最大,最大值.
故答案为:.
【变式8-1】(23-24·河南郑州·三模)如图,点M是等边三角形边的中点,P是三角形内一点,连接,将线段以A为中心逆时针旋转得到线段,连接.若,,则的最小值为 .
【答案】
【分析】本题考查旋转的性质、等边三角形的判定与性质、勾股定理、全等三角形的判定与性质、圆的有关定义以及和性质等知识,得到点Q的运动路线是解答的关键.连接,,将线段绕着点A逆时针旋转得到线段,连接,,由旋转性质可推导,是等边三角形,则,,根据圆的定义可得点Q在以H为圆心,1为半径的圆上运动,进而可知当M、Q、H共线时,最小,最小值为,根据等边三角形的性质求得值即可求解.
【详解】解:连接,,将线段绕着点A逆时针旋转得到线段,连接,,
由旋转性质得,,,即,
∴,是等边三角形,
∴,,
则点Q在以H为圆心,1为半径的圆上运动,
∵,
∴当M、Q、H共线时,最小,最小值为,
∵点M是等边三角形边的中点,,
∴,,
∴,即,
∴的最小值为,
故答案为:.
【变式8-2】(23-24九年级·湖北武汉·期中)如图,已知在中,,,将绕点A逆时针旋转.得到.点D是边的中点,点E为边上的动点,在绕点A逆时针旋转的过程中,点E的对应点是点,则线段长度的最大值与最小值的差是 .
【答案】
【分析】如图,连接,作于H,于.求出的最小值以及最大值即可解决问题.
【详解】解:如图,连接,作于H,于.
以A为圆心,以为半径作圆,与直线的右侧交点为,
以A为圆心,以为半径作圆,与直线的左侧交点为,
∵,,点D是边的中点,
∴,,
∴,
∵,
∴,
在旋转过程中,当点与重合时,的值最小,且最小值为:,
当点与重合时,的值最大,且最大值,
∴线段长度的最大值与最小值的差为:,
故答案为:.
【点睛】本题考查了旋转的性质,勾股定理,等腰三角形的三线合一性质,垂线段最短,圆的基本性质,熟练掌握勾股定理,等腰三角形的三线合一性质,垂线段最短,圆的基本性质是解题的关键.
【变式8-3】(23-24九年级·江苏镇江·阶段练习)如图,正比例函数与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的上运动,点Q是的中点,则长的最大值为( )
A. B. C. D.
【答案】A
【分析】本题考查了正比例函数与反比例函数的交点问题,三角形中位线定理,圆的性质等知识点,熟练掌握正比例函数与反比例函数的性质是解题关键.连结,根据反比例函数的中心对称性可得,即得是的中位线,所以,当经过圆心C时,取得最大值,最大值为,求出,的值,即得答案.
【详解】连结,
正比例函数与反比例函数的图象交于A、B两点,
点A与点B关于原点O对称,
,
点Q是AP的中点,
是的中位线,
,
当经过圆心C时,取得最大值,最大值为,
联立,
解得或,
,
,
,
点P在1为半径的上运动,
,
,
长的最大值为.
故选A.
【题型9 圆中角度的计算】
【例9】(23-24九年级·广东珠海·期末)如图,在平面直角坐标系中,B,C为x轴上两点,以点O为圆心画圆(直径小于),交y轴负半轴于点A,过点A作x轴平行线,点P为圆上一个动点,连接,下列说法正确的有( )
①当点P运动到第一象限,则
②当点P运动到第二象限,则
③当点P运动到第三象限,则
④当点P运动到第四象限,则
A.①② B.③④ C.①④ D.②③
【答案】D
【分析】本题考查了等腰三角形的判定及性质,平行线的性质,解题的关键是利用数形结合的思想来求解,画出每一种情况的图形,然后利用平行线的性质求解.
【详解】解:①当点P运动到第一象限,则,故①错误;
②当点P运动到第二象限,
则,故②正确;
③当点P运动到第三象限,
则,故③正确;
④当点P运动到第四象限,则,
则,故④错误,
故正确的为:②③,
故选:D.
【变式9-1】(23-24九年级·江苏连云港·阶段练习)如图,的圆心为点,以点为圆心作,且与的延长线交于点,与的延长线交于点.已知,求的度数.
【答案】
【分析】由等腰三角形的性质及三角形的内角和定理得 ,再由等腰三角形的性质及三角形外角性质得 ,继而利用三角形的外角性质即可得解.
【详解】解:∵,,
∴ ,
∵,
∴,
∵,
∴ ,
∴ ,
∵,
∴
【点睛】本题主要考查了等腰三角形的性质、三角形的内角和定理及外角性质以及圆的认识,熟练掌握三角形的内角和定理及等腰三角形的性质是解题的关键.
【变式9-2】(23-24九年级·湖南湘西·期中)如图,是半圆的直径,点是半圆上不与点、重合的一个动点,延长到点,使,是的中点,连接、.
(1)求证: ;
(2)连接,当四边形是菱形时,求的度数.
【答案】(1)见解析
(2)
【分析】(1)根据中位线的性质得到, ,由可证;
(2)根据菱形的性质得,从而证是等边三角形,利用等边三角形的性质即可求解.
【详解】(1)解:点是的中点,,
,,
.
,
,
在和中,
,
;
(2)解:连接,
四边形是菱形,
∴,
∵,
∴,
∴是等边三角形,
.
【点睛】本题主要考查全等三角形的判定与性质、等边三角形的判定及性质以及菱形的性质,解题关键是根据中位线的性质得到, ,由得出.
【变式9-3】(23-24·湖北武汉·一模)如图,在中,,C为上一点,连接.
(1)若,求的度数;
(2)若的面积与的面积之比为,求的值.
【答案】(1)∠BOC的度数为50°
(2)
【分析】(1)设,先根据等边对等角和三角形内角和定理得到,再根据建立方程求解即可;
(2)过C作于H,设,根据三角形面积之比求出,则由勾股定理得,进而得到,再利用勾股定理求出的长即可得到答案.
【详解】(1)解:设,
∵,
∴,
∵,
∴,
解得,
∴;
(2)
解:过C作于H,设,
∵的面积与的面积之比为,
∴,
∴,
∴,
∴,
∴,
在中,由勾股可得,
在中,由勾股可得,
∴.
【点睛】本题主要考查了圆的基本性质,勾股定理,等边对等角,三角形内角和定理,正确作出辅助线构造直角三角形是解题的关键.
【题型10 圆中线段长度的计算】
【例10】(23-24·上海虹口·二模)如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A的对称点),那么的长为 .
【答案】/
【分析】本题考查翻折性质,圆的基本性质,等边三角形判定与性质、勾股定理的应用,连接,由翻折得,证出是等边三角形,设,在中,根据勾股定理列方程并解出进而求出结论.
【详解】解:连接,
由翻折得:,,
,
是等边三角形,
,
,
设,则,
在中,,
,
解得:(舍去),
,
故答案为:.
【变式10-1】(23-24九年级·山东滨州·期中)如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D,若点D巧好为线段AB的中点,则AB的长度为( )
A. B.3 C. 6 D.9
【答案】C
【分析】根据直角三角形斜边上的中线的圆的性质求解即可;
【详解】连接CD,
∵以点C为圆心、CA为半径的圆与AB交于点D,AC=3,
∴,
又∵在Rt△ABC中,∠ACB=90°,D为线段AB的中点,
∴,
∴;
故选C.
【点睛】本题主要考查了直角三角形斜边上的中线是斜边的一半和圆的性质,准确计算是解题的关键.
【变式10-2】(23-24九年级·浙江绍兴·期末)如图,正方形的边长为4,点在边上,,点在上,与直线交于点(点在点右侧),则的长度为( )
A. B.8 C. D.
【答案】C
【分析】连接,由正方形性质可得,,,然后用勾股定理求出半径,再求出的长即可.
【详解】解:连接,
∵正方形的边长为4,,
∴,,,
∴在中,,
∴,
∴,
∴在中,,
故选:C.
【点睛】本题考查正方形的性质、圆的性质及勾股定理等知识,解题的关键是熟练掌握有关圆的性质,属于中考常考题型.
【变式10-3】(23-24·广东江门·模拟预测)综合探究
如图,在扇形中,是上异于的动点,过点作于点,作于点,连接,点在线段上,且.
(1)求证:四边形是平行四边形.
(2)当点在上运动时,在中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.
(3)求证:是定值.
【答案】(1)见解析;
(2)存在,1;
(3)见解析.
【分析】本题主要考查圆的基本性质以及勾股定理:
(1)道德证明四边形是矩形,得,同理可证,得出四边形是平行四边形.
(2)根据点A是上的点,,得出,由得出;
(3)过点作于点.设,则,求出,,计算出,进一步可得出结论
【详解】(1)证明:如图,连接交于点.
,
,
四边形是矩形,
.
,
,
,
四边形是平行四边形.
(2)解:存在,线段的长度不变.
∵点A是上的点,
在矩形中,.
,
.
(3)解:如图,过点作于点.
设,则.
由,得,
.
,
,
,
是定值.
21世纪教育网(www.21cnjy.com)
同课章节目录
