人教版2024-2025九年级数学上册同步讲义专题专题24.8正多边形与圆【九大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025九年级数学上册同步讲义专题专题24.8正多边形与圆【九大题型】(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 07:14:13 | ||
图片预览

文档简介
专题24.8 正多边形与圆【九大题型】
【人教版】
【题型1 求正多边形中心角】 2
【题型2 由正多边形中心角求边数】 3
【题型3 尺规作正多边形】 3
【题型4 正多边形和圆中求线段长度】 5
【题型5 正多边形和圆中求角度】 6
【题型6 正多边形和圆中求周长】 7
【题型7 正多边形和圆中求面积】 8
【题型8 正多边形和圆中求最值】 9
【题型9 正多边形和圆中的证明】 10
知识点:正多边形和圆
(1)正多边形的有关概念
正多边形与圆的关系非常密切,把圆分成n(n就是大于2的自然数)等份,顺次连接各分点所的的多边形就是这个圆的内接正多边形,这个圆就就是这个正多边形的外接圆。
正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心。
正多边形的半径:外接圆的半径叫做正多边形的半径。
正多边形的中心角:正多边形每一条边所对的圆心角叫做正多边形的中心角。
正多边形的边心距:中心到正多边形一边的距离叫做正多边形的边心距。
(2)正多边形的有关计算
中心角 边心距 周长 面积
为边数;为边心距;为半径;为边长
(3)正多边形每个内角度数为,每个外角度数为
【题型1 求正多边形中心角】
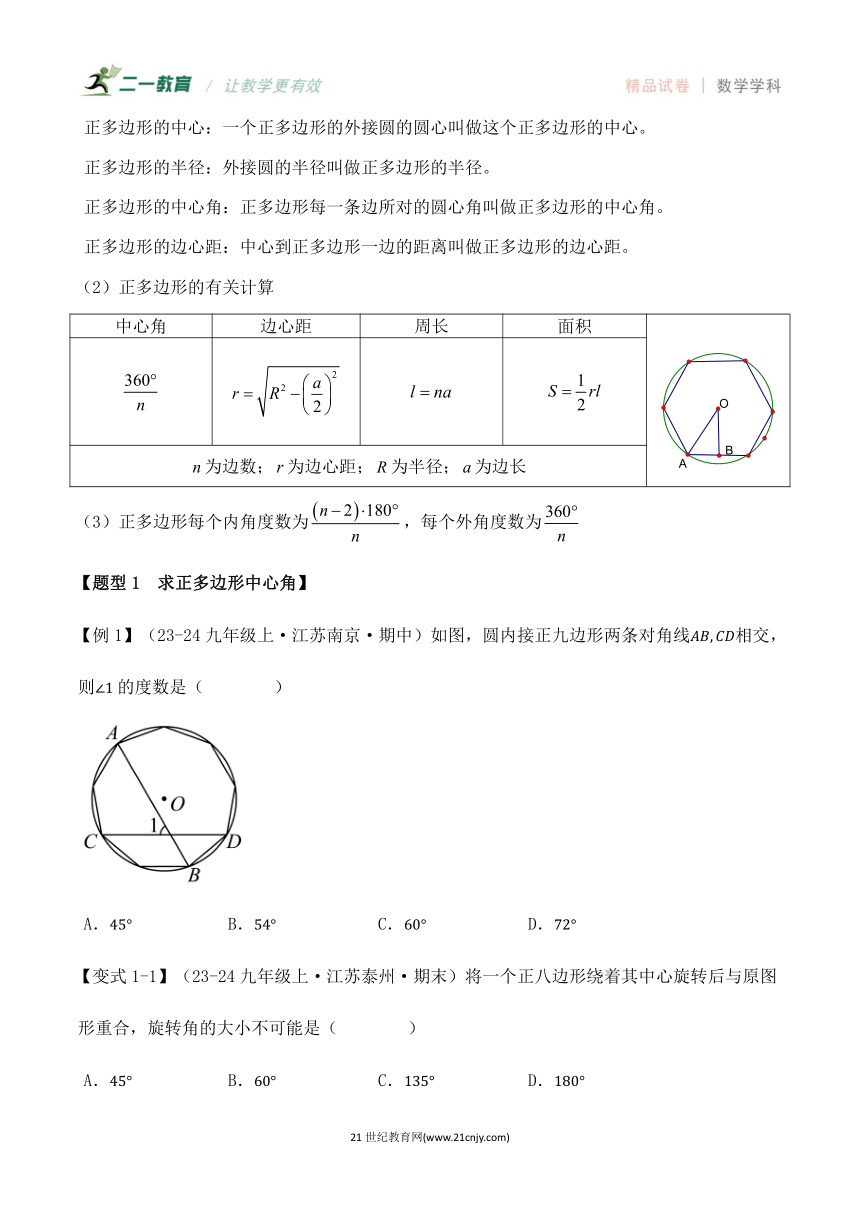
【例1】(23-24九年级上·江苏南京·期中)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
【变式1-1】(23-24九年级上·江苏泰州·期末)将一个正八边形绕着其中心旋转后与原图形重合,旋转角的大小不可能是( )
A. B. C. D.
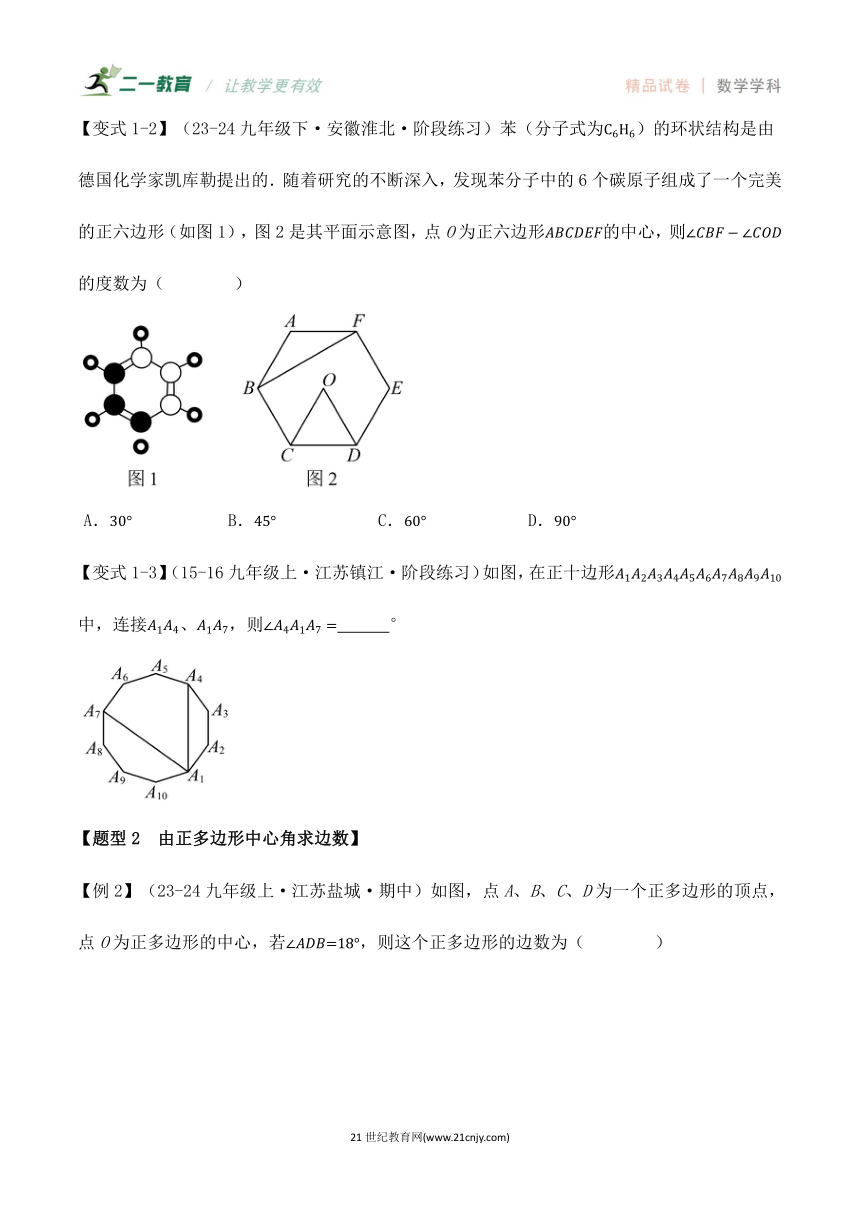
【变式1-2】(23-24九年级下·安徽淮北·阶段练习)苯(分子式为)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2是其平面示意图,点O为正六边形的中心,则的度数为( )
A. B. C. D.
【变式1-3】(15-16九年级上·江苏镇江·阶段练习)如图,在正十边形中,连接、,则 °
【题型2 由正多边形中心角求边数】
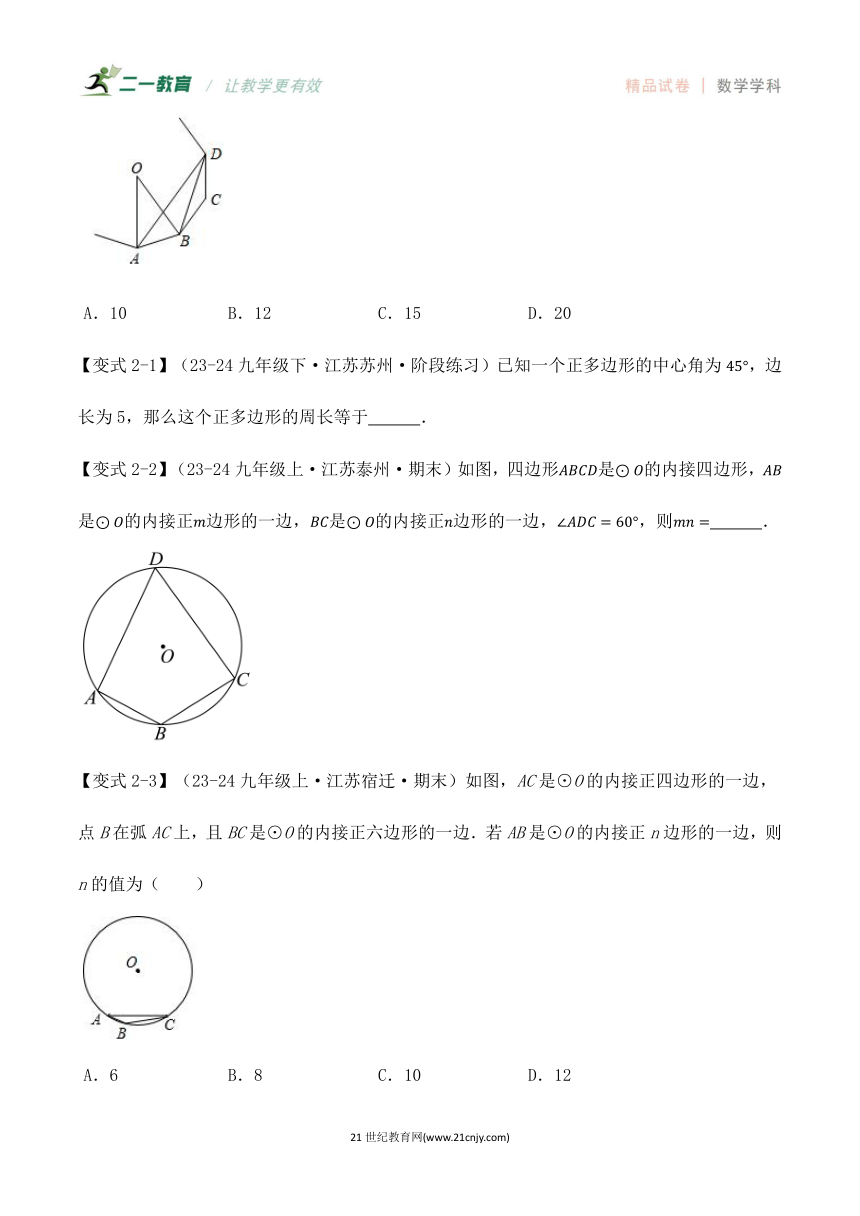
【例2】(23-24九年级上·江苏盐城·期中)如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
【变式2-1】(23-24九年级下·江苏苏州·阶段练习)已知一个正多边形的中心角为,边长为5,那么这个正多边形的周长等于 .
【变式2-2】(23-24九年级上·江苏泰州·期末)如图,四边形是的内接四边形,是的内接正边形的一边,是的内接正边形的一边,,则 .
【变式2-3】(23-24九年级上·江苏宿迁·期末)如图,AC是⊙O的内接正四边形的一边,点B在弧AC上,且BC是⊙O的内接正六边形的一边.若AB是⊙O的内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
【题型3 尺规作正多边形】
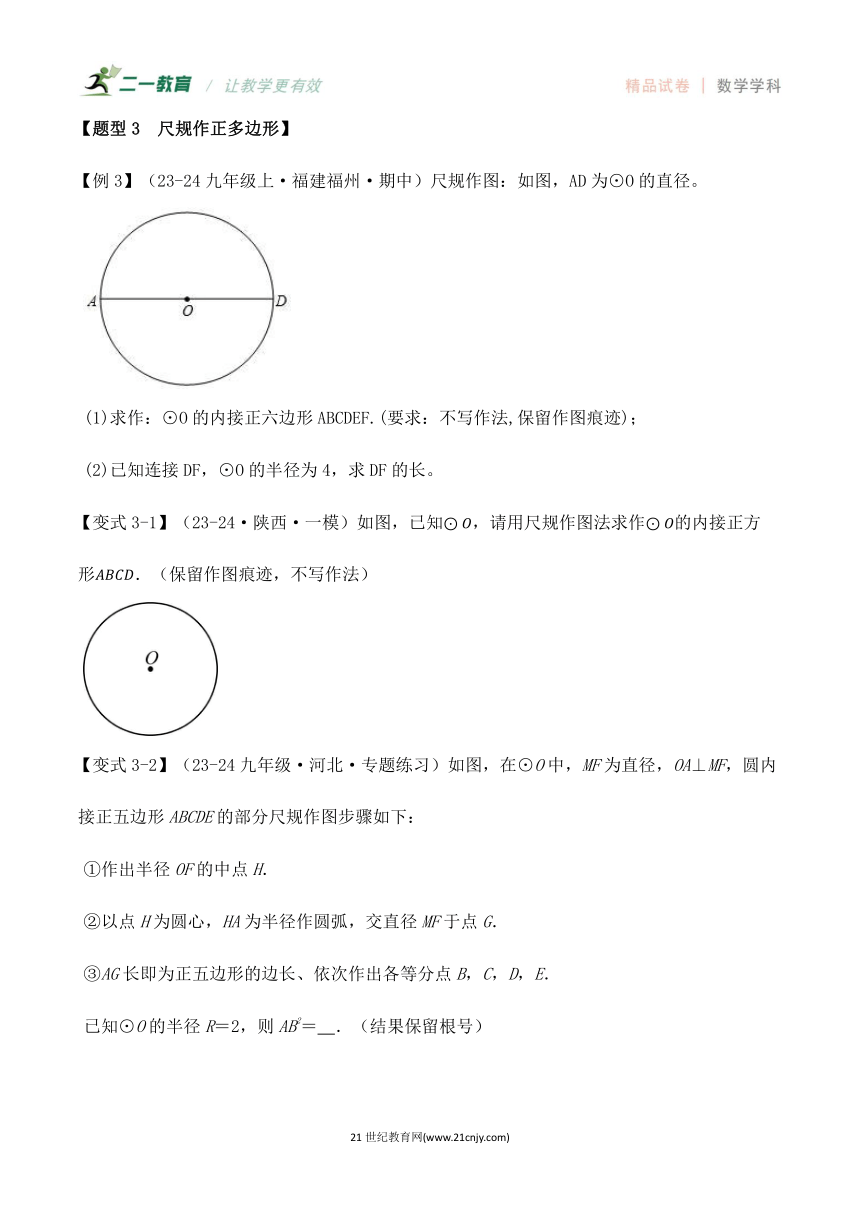
【例3】(23-24九年级上·福建福州·期中)尺规作图:如图,AD为⊙O的直径。
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
【变式3-1】(23-24·陕西·一模)如图,已知,请用尺规作图法求作的内接正方形.(保留作图痕迹,不写作法)
【变式3-2】(23-24九年级·河北·专题练习)如图,在⊙O中,MF为直径,OA⊥MF,圆内接正五边形ABCDE的部分尺规作图步骤如下:
①作出半径OF的中点H.
②以点H为圆心,HA为半径作圆弧,交直径MF于点G.
③AG长即为正五边形的边长、依次作出各等分点B,C,D,E.
已知⊙O的半径R=2,则AB2= .(结果保留根号)
【变式3-3】(2024·江苏无锡·一模)尺规作图:
(1)请在图①中以矩形的边为边作菱形,使得点E在上;
(2)请在图②中以矩形的边为直径作,并在上确定点P,使得的面积与矩形的面积相等.
【题型4 正多边形和圆中求线段长度】
【例4】(23-24九年级上·河北石家庄·期中)如图,半径为2的是正六边形的外接圆,则边心距的长度为( )
A.1 B. C. D.2
【变式4-1】(23-24九年级上·江苏南京·期中)如图,六边形ABCDEF是⊙O的内接正六边形,分别以点A、D为圆心,AE长为半径作弧,在⊙O外交于点G,连接OG.若⊙O的半径为1,则OG的长度为 .
【变式4-2】(23-24九年级·全国·假期作业)如图,正方形和正三角形内接于,、交于、,若正方形的边长是4,则的长度为
A. B. C. D.
【变式4-3】(23-24九年级上·浙江绍兴·阶段练习)如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
【题型5 正多边形和圆中求角度】
【例5】(23-24九年级上·广东东莞·期末)如图,正六边形内接于,边长为2.
(1)求的直径的长;
(2)求的度数.
【变式5-1】(2024·宁夏银川·二模)如图,正五边形内接于,P为劣弧上的动点,则的大小为 .
【变式5-2】(23-24九年级上·全国·单元测试)如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
【变式5-3】(2024·安徽淮北·二模)如图,是正五边形和正六边形的外接圆,连接和,则的度数为 .
【题型6 正多边形和圆中求周长】
【例6】(2024九年级上·江苏·专题练习)如图,是正六边形的外接圆,若的半径为6,则四边形的周长是( )
A. B. C. D.
【变式6-1】(23-24九年级上·浙江温州·期中)如图,六边形是的内接正六边形,记的周长为,正六边形的周长为,则的值为 .
【变式6-2】(23-24九年级上·河南许昌·期末)如图,正六边形内接于,已知的半径为1,连接,则四边形的周长为( )
A.6 B. C.4 D.
【变式6-3】(23-24九年级上·江苏无锡·期中)如图,正方形内接于⊙O,线段在对角线上运动,若⊙O的周长为,,则周长的最小值是 .
【题型7 正多边形和圆中求面积】
【例7】(2024·江苏南京·三模)如图,表示中去掉内接正三角形部分的面积,表示中去掉内接正六边形部分的面积,和的半径均为,则 .(填“、或”)
【变式7-1】(23-24九年级上·全国·课后作业)如图,的半径为,以的内接正八边形的一边为边在内作正方形,则正方形的面积为 .
【变式7-2】(2024·江苏无锡·一模)魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积. 如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.1 B. C.3 D.4
【变式7-3】(23-24九年级上·安徽芜湖·阶段练习)如图,的半径为,是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
【题型8 正多边形和圆中求最值】
【例8】(23-24九年级上·山东临沂·期末)如图,的圆心与正方形的中心重合,已知的半径和正方形的边长都为2,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.1 C. D.
【变式8-1】(23-24·陕西西安·一模)如图,点P为⊙上一点,连接OP,且,点A为OP上一动点,点B为⊙上一动点,连接AB,以线段AB为边在⊙内构造矩形ABCD,且点C在⊙上,则矩形ABCD面积的最大值为 .
【变式8-2】(23-24九年级上·内蒙古鄂尔多斯·期末)如图,点是边长为2的正六边形内的一点(不包括边界),且,是上的一点,是的中点,则的最小值为 .
【变式8-3】(23-24·广东广州·中考真题)如图,为等边的外接圆,半径为2,点在劣弧上运动(不与点重合),连接,,.
(1)求证:是的平分线;
(2)四边形的面积是线段的长的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置,的周长有最小值,随着点的运动,的值会发生变化,求所有值中的最大值.
【题型9 正多边形和圆中的证明】
【例9】(23-24九年级上·浙江·期末)如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
【变式9-1】(23-24·湖北武汉·模拟预测)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【变式9-2】(23-24九年级上·湖北武汉·期中)如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
【变式9-3】(23-24九年级上·全国·单元测试)如图,已知的内接正十边形,交,于,,求证:
(1);
(2).21世纪教育网(www.21cnjy.com)
专题24.8 正多边形与圆【九大题型】
【人教版】
【题型1 求正多边形中心角】 2
【题型2 由正多边形中心角求边数】 5
【题型3 尺规作正多边形】 8
【题型4 正多边形和圆中求线段长度】 13
【题型5 正多边形和圆中求角度】 18
【题型6 正多边形和圆中求周长】 21
【题型7 正多边形和圆中求面积】 25
【题型8 正多边形和圆中求最值】 29
【题型9 正多边形和圆中的证明】 35
知识点:正多边形和圆
(1)正多边形的有关概念
正多边形与圆的关系非常密切,把圆分成n(n就是大于2的自然数)等份,顺次连接各分点所的的多边形就是这个圆的内接正多边形,这个圆就就是这个正多边形的外接圆。
正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心。
正多边形的半径:外接圆的半径叫做正多边形的半径。
正多边形的中心角:正多边形每一条边所对的圆心角叫做正多边形的中心角。
正多边形的边心距:中心到正多边形一边的距离叫做正多边形的边心距。
(2)正多边形的有关计算
中心角 边心距 周长 面积
为边数;为边心距;为半径;为边长
(3)正多边形每个内角度数为,每个外角度数为
【题型1 求正多边形中心角】
【例1】(23-24九年级上·江苏南京·期中)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
【答案】C
【分析】本题考查了正多边形与圆,圆周角定理,三角形外角的性质,添加辅助线是解题的关键.根据正多边形与圆求出相应的圆心角度数,再根据圆周角定理和三角形外角的性质可得答案.
【详解】解:如图,设这个正九边形的外接圆为,
则,
∴,
∴,
故选:C.
【变式1-1】(23-24九年级上·江苏泰州·期末)将一个正八边形绕着其中心旋转后与原图形重合,旋转角的大小不可能是( )
A. B. C. D.
【答案】B
【分析】本题考查了正多边形的性质,解题的关键是掌握正多边形中心角的度数为,先求出正八边形中心角的度数,即可解答.
【详解】解:正八边形的中心角为,
∵,
∴旋转角的大小可能是,,,
∵不是的整数倍,
∴旋转角的大小不能是,
故选:B.
【变式1-2】(23-24九年级下·安徽淮北·阶段练习)苯(分子式为)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2是其平面示意图,点O为正六边形的中心,则的度数为( )
A. B. C. D.
【答案】A
【分析】根据点O为正六边形的中心,得到,,继而得到,,解答即可.
本题考查了正多边形的性质,中心角的计算,等腰三角形的三线合一性质,熟练掌握多边形的性质和中心角的计算是解题的关键.
【详解】∵点O为正六边形的中心,
∴,
∴,
∴,
∴,
故选:A.
【变式1-3】(15-16九年级上·江苏镇江·阶段练习)如图,在正十边形中,连接、,则 °
【答案】54
【分析】设正十边形的圆心O,连接A7O、A4O,再求出∠A7OA4,最后运用圆周角定理解答即可.
【详解】解:如图:设正十边形的圆心O,连接A7O、A4O,
∵正十边形的各边都相等
∴∠A7OA4=×360°=108°
∴108°×=54°.
故填54.
【点睛】本题主要考查了正多边形和圆以及圆周角定理,根据题意正确作出辅助线、构造出圆周角是解答本题的关键.
【题型2 由正多边形中心角求边数】
【例2】(23-24九年级上·江苏盐城·期中)如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
【答案】A
【分析】作正多边形的外接圆,根据圆周角定理得到,根据中心角的定义即可求解.
【详解】解:如图,作正多边形的外接圆,
∵,
∴,
∴这个正多边形的边数为.
故选:A.
【点睛】此题主要考查正多边形的性质,解题的关键是熟知圆周角定理.
【变式2-1】(23-24九年级下·江苏苏州·阶段练习)已知一个正多边形的中心角为,边长为5,那么这个正多边形的周长等于 .
【答案】40
【分析】利用正多边形的中心角求出正多边形的边数,最后根据正多边形的性质求出其周长.
【详解】解:一个正多边形的中心角为,
这个正多边形的边数为:,
这个正多边形的周长为:.
故答案为:40.
【点睛】本题主要考查了正多边形的性质,解题的关键在于知道中心角与边长的关系.
【变式2-2】(23-24九年级上·江苏泰州·期末)如图,四边形是的内接四边形,是的内接正边形的一边,是的内接正边形的一边,,则 .
【答案】48或36
【分析】本题考查了正多边形与圆:把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆;熟练掌握正多边形的有关概念.连接,如图,利用正多边形与圆,分别计算的内接正m边形与内接正n边形的中心角得到,根据,得到m,n的值,然后代入计算即可.
【详解】解:连接,如图,
,
,
,
,
,
m,n的中有一个值必是3的倍数,且均为正整数,
设(均为正整数),则,
(n为正整数),
当时,(不符合题意);
当时,,则;
当时,(不符合题意);
当时,,则;
当时,(不符合题意);
当时,,(不符合题意);
;
当时,n均不为正整数,(不符合题意);
综上,的值为48或36.
【变式2-3】(23-24九年级上·江苏宿迁·期末)如图,AC是⊙O的内接正四边形的一边,点B在弧AC上,且BC是⊙O的内接正六边形的一边.若AB是⊙O的内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
【答案】D
【分析】连接AO、BO、CO,根据中心角度数=360°÷边数n,分别计算出∠AOC、∠BOC的度数,根据角的和差则有∠AOB=30°,根据边数n=360°÷中心角度数即可求解.
【详解】连接AO、BO、CO,
∵AC是⊙O内接正四边形的一边,
∴∠AOC=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠BOC=360°÷6=60°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故选:D.
【点睛】本题考查正多边形和圆,解题的关键是根据正方形的性质、正六边形的性质求出中心角的度数.
【题型3 尺规作正多边形】
【例3】(23-24九年级上·福建福州·期中)尺规作图:如图,AD为⊙O的直径。
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
【答案】(1)见解析;(2)4
【分析】(1)如图,在⊙O上依次截取六段弦,使它们都等于OA,从而得到正六边形ABCDEF;
(2)连接OF,可得△OFE是等边三角形,边长为4,可求得∠OEF=60°,∠DFE=30°,设BE与DF交于G点,可得∠FGE=90°,即可求得FG的长,进而求得FD的长.
【详解】(1)如图,正六边形ABCDEF为所作;
(2)连接OF,设BE与DF交于G点
∵六边形ABCDEF为正六边形
∴∠FOE=60°,DF=DE,∠DEF=120°
∴∠DFE=30°
∵OE=OF
∴△FOE为等边三角形
∴EF=OE=4,∠OEF=60°
∴∠FGE=90°
∴EG=OE=2
∴FG=
∴FD=2FG=
【点睛】此题主要考查了复杂作图及正多边形的计算,关键是掌握圆的内接正六边形的边长等于圆的半径.
【变式3-1】(23-24·陕西·一模)如图,已知,请用尺规作图法求作的内接正方形.(保留作图痕迹,不写作法)
【答案】见解析
【分析】本题考查了作正方形,考查了圆的基本性质,正方形的判定;先在圆上确定一点,连接并延长交于点,再作的垂直平分线交于B、D,连接,则四边形就是所求作的内接正方形.
【详解】解:如图,正方形为所作.
垂直平分,为的直径,
为的直径,
,
,,,
四边形是矩形
,
四边形是正方形,
又都在圆上,
四边形是的内接正方形.
【变式3-2】(23-24九年级·河北·专题练习)如图,在⊙O中,MF为直径,OA⊥MF,圆内接正五边形ABCDE的部分尺规作图步骤如下:
①作出半径OF的中点H.
②以点H为圆心,HA为半径作圆弧,交直径MF于点G.
③AG长即为正五边形的边长、依次作出各等分点B,C,D,E.
已知⊙O的半径R=2,则AB2= .(结果保留根号)
【答案】
【分析】连接AG,由作图可知,OA=2,H为OF中点,可求OH=,由勾股定理得AH=,可求OG=﹣1,由勾股定理AB2=AG2=OA2+OG2=4+(﹣1)2=10﹣2即可.
【详解】解:连接AG,由作图可知,OA=2,OH=1,H为OF中点,
∴OH=,
在Rt△OAH中,由勾股定理
∴AH=,
∵AH=HG=,
∴OG=GH﹣OH=﹣1,
在Rt△AOG中,由勾股定理得,
∴AB2=AG2=OA2+OG2=4+(﹣1)2=10﹣2.
故答案为:10﹣2.
【点睛】本题考查尺规作圆内接正五边形的方法与步骤,线段垂直平分线,勾股定理,作圆弧,掌握圆内接正五边形的方法与步骤,线段垂直平分线,勾股定理,作圆弧的方法是解题关键.
【变式3-3】(2024·江苏无锡·一模)尺规作图:
(1)请在图①中以矩形的边为边作菱形,使得点E在上;
(2)请在图②中以矩形的边为直径作,并在上确定点P,使得的面积与矩形的面积相等.
【答案】(1)见解析
(2)见解析
【分析】(1)结合菱形的判定,以点D为圆心,的长为半径画弧,交为点E,再分别以点E、点A为圆心,的长为半径画弧,两弧交于点F,连接、、即可;
(2)作线段的垂直平分线,交于点O,以点O为圆心,的长为半径画圆,即可得,以点O为圆心,的长为半径画弧,在的上方交于点E,再作,作直线,分别交于点、,即可求解.
【详解】(1)解:如图,菱形即为所求,
(2)解:如图,点、即为所求,
【点睛】本题考查作图 复杂作图、菱形的判定、矩形的性质、垂直平分线的性质,理解题意、灵活运用相关知识是解题的关键.
【题型4 正多边形和圆中求线段长度】
【例4】(23-24九年级上·河北石家庄·期中)如图,半径为2的是正六边形的外接圆,则边心距的长度为( )
A.1 B. C. D.2
【答案】B
【分析】如图所示,连接,求出,进而证明是等边三角形,得到,求出,即可利用勾股定理求出答案.
【详解】解:如图所示,连接,
由题意得,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,
故选B.
【点睛】本题主要考查了正多边形与圆,勾股定理,等边三角形的性质与判断,正确作出辅助线构造直角三角形是解题的关键.
【变式4-1】(23-24九年级上·江苏南京·期中)如图,六边形ABCDEF是⊙O的内接正六边形,分别以点A、D为圆心,AE长为半径作弧,在⊙O外交于点G,连接OG.若⊙O的半径为1,则OG的长度为 .
【答案】
【分析】连接AG,AD,AE,OE,过点O作OH⊥AE于点H,解直角三角形求出AE,再利用勾股定理求出OG即可.
【详解】解:如图,连接AG,AD,AE,OE,过点O作OH⊥AE于点H.
∵OH⊥AE,
∴AH=EH,
∵∠AOE=120°,
∴∠OAE=∠OEA=30°,
OH=OA=,AH=,
∴,
∴,
在和中
∴
∴
∴
故答案为:.
【点睛】此题考查了圆的性质,全等三角形的判定,勾股定理,解题的关键是熟练掌握相关基本性质.
【变式4-2】(23-24九年级·全国·假期作业)如图,正方形和正三角形内接于,、交于、,若正方形的边长是4,则的长度为
A. B. C. D.
【答案】A
【分析】连接交于,连接,根据正方形的性质、等边三角形的性质及等腰三角形的性质即可求解.
【详解】解:连接交于,连接,
四边形是正方形,
,
是的直径,
是等腰直角三角形,
,
,
是等边三角形,
,,
,
,
,,
,
是等腰直角三角形,
.
故选:.
【点睛】本题考查正多边形与圆的关系,涉及到特殊锐角三角函数值、正方形的性质、等边三角形的性质及等腰三角形的性质,解题的关键是综合运用所学知识.
【变式4-3】(23-24九年级上·浙江绍兴·阶段练习)如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
【答案】(1)
(2)
【分析】(1)连接,,根据正六边形的性质可得,再根据圆的半径都相等可得是等边三角形,进而可求解.
(2)连接,,由为的直径,得,利用勾股定理及中点的性质即可求解.
【详解】(1)解:连接,,如图:
六边形是正六边形,
,
又 ,是的半径,且半径为,
,
是等边三角形,
.
(2)连接,,如图:
则为的直径,
,,
由(1)得:,
在中,,
,
G为的中点,
,
在中,,
.
【点睛】本题考查了正多边形的性质、等边三角形的判定及性质、勾股定理及圆周角,熟练掌握基础知识,借助适当的辅助线解决问题是解题的关键.
【题型5 正多边形和圆中求角度】
【例5】(23-24九年级上·广东东莞·期末)如图,正六边形内接于,边长为2.
(1)求的直径的长;
(2)求的度数.
【答案】(1)
(2)
【分析】本题考查正多边形和圆,圆周角定理:
(1)连接,求出的度数,得到是等边三角形,得到,即可得出结果;
(2)根据圆周角定理,即可得出结果.
【详解】(1)解:连接.
∵正六边形内接于,
∴,
又,
∴是等边三角形.
∴.
∴.
(2)解:∵,
∴.
【变式5-1】(2024·宁夏银川·二模)如图,正五边形内接于,P为劣弧上的动点,则的大小为 .
【答案】/144度
【分析】本题考查了正多边形和圆,圆内接四边形的性质,作出圆中常用辅助线是解题的关键.连接,正多边形的性质得的度数,由圆周角定理得的度数,再圆内接四边形的性质即可求解.
【详解】解:如图,连接,
∵五边形是正五边形,
∴,
∵,
∴,
∵正五边形的外接圆为,
∴四边形是内接四边形,
∴,
∴;
故答案为:.
【变式5-2】(23-24九年级上·全国·单元测试)如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
【答案】
【分析】本题考查的是正多边形和圆、圆周角定理的应用,连接、、,根据正多边形和圆的知识求出正八边形的中心角的度数,根据圆周角定理求出的度数.
【详解】解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
【变式5-3】(2024·安徽淮北·二模)如图,是正五边形和正六边形的外接圆,连接和,则的度数为 .
【答案】/24度
【分析】本题考查正多边形与圆,连接,根据正多边形的性质可得:,进而得到,,再根据即可求解.
【详解】解:连接,
根据题意得:,
,
,
,
故答案为:.
【题型6 正多边形和圆中求周长】
【例6】(2024九年级上·江苏·专题练习)如图,是正六边形的外接圆,若的半径为6,则四边形的周长是( )
A. B. C. D.
【答案】C
【分析】本题考查正多边形和圆,矩形,掌握正六边形的性质,矩形的性质以及直角三角形的边角关系是正确解答的关键.根据正六边形的性质,矩形的性质以及直角三角形的边角关系求出,即可.
【详解】解:如图,连接,,,过点作于点,则,
点是正六边形的中心,
,
,
是正三角形,
,
在中,,,
,
,
四边形的周长是,
故选:C
【变式6-1】(23-24九年级上·浙江温州·期中)如图,六边形是的内接正六边形,记的周长为,正六边形的周长为,则的值为 .
【答案】
【分析】本题主要考查了正六边形的性质,含30°角的直角三角形的性质,设正六边形的边长为a,利用含角的直角三角形的性质求出,从而得出的长,进而解决问题.
【详解】解:设正六边形的边长为a,
连接,交于H,如下图:
∵六边形是的内接正六边形,
∴,,,
∴
∴,
∴
∴,
由正六边形的性质知,是等边三角形,
∴,
故答案为:.
【变式6-2】(23-24九年级上·河南许昌·期末)如图,正六边形内接于,已知的半径为1,连接,则四边形的周长为( )
A.6 B. C.4 D.
【答案】C
【分析】本题考查的是正多边形和圆,连接,则, 均为等边三角形.所以.即得出四边形的周长.熟知正六边形的性质是解答此题的关键.
【详解】解:连接,如解图所示.
六边形是正六边形,
.
又,
, 均为等边三角形.
.
四边形的周长为,
故选:.
【变式6-3】(23-24九年级上·江苏无锡·期中)如图,正方形内接于⊙O,线段在对角线上运动,若⊙O的周长为,,则周长的最小值是 .
【答案】/
【分析】过点作,令;可推出四边形为平行四边形,有;根据可知当时,周长有最小值.
【详解】解:过点作,令
∵⊙O的周长为,
∴⊙O的半径为
∴
∵且
∴四边形为平行四边形
∴
由正方形的对称性可得:
∴
∴
故:当时,周长有最小值
此时:
∴周长的最小值是
故答案为:
【点睛】本题考查了正方形的性质、平行四边形的判定与性质等.推出当时,周长有最小值是解题关键.
【题型7 正多边形和圆中求面积】
【例7】(2024·江苏南京·三模)如图,表示中去掉内接正三角形部分的面积,表示中去掉内接正六边形部分的面积,和的半径均为,则 .(填“、或”)
【答案】
【分析】本题考查了圆的内接正多边形,分别求出、,再根据作差法即可求解,掌握圆的内接正多边形的性质是解题的关键.
【详解】解:如图,连接,过作于,连接,过作于,
在图中,,,,,
∴,,
∴,
∴
,
在图中,,,
∴为等边三角形,
∵,
∴,
∴,
∴,
,
∴,
∴,
∴,
故答案为:.
【变式7-1】(23-24九年级上·全国·课后作业)如图,的半径为,以的内接正八边形的一边为边在内作正方形,则正方形的面积为 .
【答案】
【分析】本题考查了正多边形和圆,等腰直角三角形的判定和性质,勾股定理;
连接,,过A作于E,求出,可得是等腰直角三角形,然后求出,进而求出,然后利用勾股定理求出即可得到答案.
【详解】解:如图,连接,,过A作于E,则,
∵是正八边形的中心角,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
∴正方形的面积为:,
故答案为:.
【变式7-2】(2024·江苏无锡·一模)魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积. 如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.1 B. C.3 D.4
【答案】C
【分析】本题考查了正多边形与圆,三角形的面积的计算,解直角三角形,正确的作出辅助线是解题的关键.过作于,得到圆的内接正十二边形的圆心角为,根据三角形的面积公式即可得到结论.
【详解】解:如图,过作于,
圆的内接正十二边形的圆心角为,
,
,
,
这个圆的内接正十二边形的面积为,
故选:C
【变式7-3】(23-24九年级上·安徽芜湖·阶段练习)如图,的半径为,是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
【答案】A
【分析】连接、,根据平行四边形的性质得,再根据圆周角定理得为的直径,利用圆周角定理得到,根据含的直角三角形三边的关系得到,然后根据矩形的面积公式求解.
【详解】解:连接、,如图,
四边形为平行四边形,
,
,
,
为的直径,
,
为等边三角形,
,
,
而,
,
在中,,,
矩形的面积.
故选:A.
【点睛】本题考查了三角形外接圆与外心,垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、等边三角形的性质和矩形的性质,综合运用以上知识是解题的关键.
【题型8 正多边形和圆中求最值】
【例8】(23-24九年级上·山东临沂·期末)如图,的圆心与正方形的中心重合,已知的半径和正方形的边长都为2,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.1 C. D.
【答案】D
【分析】此题考查了圆与正多边形的性质,勾股定理,设正方形四个顶点分别为,连接并延长,交于点,由题意可得,的长度为圆上任意一点到正方形边上任意一点距离的最小值,求解即可.
【详解】解:设正方形四个顶点分别为,连接并延长,交于点,过点作,如下图:
则的长度为圆上任意一点到正方形边上任意一点距离的最小值,
由题意可得:,,
由勾股定理可得:,
∴,
故选:D.
【变式8-1】(23-24·陕西西安·一模)如图,点P为⊙上一点,连接OP,且,点A为OP上一动点,点B为⊙上一动点,连接AB,以线段AB为边在⊙内构造矩形ABCD,且点C在⊙上,则矩形ABCD面积的最大值为 .
【答案】32
【分析】根据当圆的半径确定以后,圆内接正方形是圆内接矩形中面积最大的,进而求得圆内接正方形的面积,则矩形ABCD面积的最大值为圆内接正方形面积,据此求解即可.
【详解】如图,四边形BCEF是圆O的内接正方形,当圆的半径确定以后,圆内接正方形是圆内接矩形中面积最大的;
点A,D分别是正方形的对边BF,CE的中点,
此时矩形ABCD的面积恰好是正方形BCEF的面积,
圆O的直径PQ恰好经过点A,D,
连接BE ,
四边形BCEF是圆O的内接正方形,OP=4,
BE = PQ = 2OP =8,BC = CE,
∠C= 90°,
BC2 + CE2 = 2BO2 = BE2 = 8,
BC2=32,即S正方形BCEF=32,
如图,当重合时,当四点都在圆上时,四边形是正方形
矩形ABCD面积的最大值为32.
故答案为:32.
【点睛】本题考查了圆内接四边形,将问题转化为圆内接四边形是解题的关键.
【变式8-2】(23-24九年级上·内蒙古鄂尔多斯·期末)如图,点是边长为2的正六边形内的一点(不包括边界),且,是上的一点,是的中点,则的最小值为 .
【答案】2
【分析】本题考查了正多边形,轴对称的性质,等边三角形的判定与性质,直角三角形斜边中线的性质等知识.取中点O,中点,连接,,延长、相交于点T,利用轴对称的性质可得,从而得出当共线时,的最小值为,然后利用直角三角形斜边中线的性质求出,证明,为等边三角形,即可求解.
【详解】解:取中点O,中点,连接,,延长、相交于点T,
,
∵正六边形关于直线对称,
∴,也关于直线对称,
∴,
∵,O为中点,
∴,
∴,
当共线时,,
∴的最小值为,
∵正六边形的边长为2,
∴,,
∴是等边三角形,
∴,,
∵,O为中点,Q为中点,
∴,,
∴,
∴是等边三角形,
∴,
∴,
∴的最小值为2.
故答案为:2.
【变式8-3】(23-24·广东广州·中考真题)如图,为等边的外接圆,半径为2,点在劣弧上运动(不与点重合),连接,,.
(1)求证:是的平分线;
(2)四边形的面积是线段的长的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置,的周长有最小值,随着点的运动,的值会发生变化,求所有值中的最大值.
【答案】(1)详见解析;(2)是, ;(3)
【分析】(1)根据等弧对等角的性质证明即可;
(2)延长DA到E,让AE=DB,证明△EAC≌△DBC,即可表示出S的面积;
(3)作点D关于直线BC、AC的对称点D1、D2,当D1、M、N、D共线时△DMN取最小值,可得t=D1D2,有对称性推出在等腰△D1CD2中,t=,D与O、C共线时t取最大值即可算出.
【详解】(1)∵△ABC为等边三角形,BC=AC,
∴ ,都为圆,
∴∠AOC=∠BOC=120°,
∴∠ADC=∠BDC=60°,
∴DC是∠ADB的角平分线.
(2)是.
如图,延长DA至点E,使得AE=DB.
连接EC,则∠EAC=180°-∠DAC=∠DBC.
∵AE=DB,∠EAC=∠DBC,AC=BC,
∴△EAC≌△DBC(SAS),
∴∠E=∠CDB=∠ADC=60°,
故△EDC是等边三角形,
∵DC=x,∴根据等边三角形的特殊性可知DC边上的高为
∴.
(3)依次作点D关于直线BC、AC的对称点D1、D2,根据对称性
C△DMN=DM+MN+ND=D1M+MN+ND2.
∴D1、M、N、D共线时△DMN取最小值t,此时t=D1D2,
由对称有D1C=DC=D2C=x,∠D1CB=∠DCB,∠D2CA=∠DCA,
∴∠D1CD2=∠D1CB+∠BCA+∠D2CA=∠DCB+60°+∠DCA=120°.
∴∠CD1D2=∠CD2D1=60°,
在等腰△D1CD2中,作CH⊥D1D2,
则在Rt△D1CH中,根据30°特殊直角三角形的比例可得D1H=,
同理D2H=
∴t=D1D2=.
∴x取最大值时,t取最大值.
即D与O、C共线时t取最大值,x=4.
所有t值中的最大值为.
【点睛】本题考查圆与正多边形的综合以及动点问题,关键在于结合题意作出合理的辅助线转移已知量.
【题型9 正多边形和圆中的证明】
【例9】(23-24九年级上·浙江·期末)如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
【答案】(1)证明见解析
(2)
【分析】(1)如图,连接AE,AD,AC,根据正六边形的性质得到EF=ED=CD=BC,求得,于是得到∠FAE=∠EAD=∠DAC=∠CAB,即可得到结论;
(2)如图,过O作OG⊥DE于G,连接OE,设⊙O的半径为r,推出△ODE是等边三角形,得到DE=OD=r,∠OED=60°,根据勾股定理得到OGr,根据三角形和圆的面积公式即可得到结论.
【详解】(1)证明:如图,连接AE,AD,AC,
∵六边形ABCDEF是⊙O的内接正六边形,
∴EF=ED=CD=BC,
∴,
∴∠FAE=∠EAD=∠DAC=∠CAB,
∴过顶点A的三条对角线四等分∠BAF;
(2)解:如图,过O作OG⊥DE于G,连接OE,
设⊙O的半径为r,
∵∠DOE60°,OD=OE=r,
∴△ODE是等边三角形,
∴DE=OD=r,∠OED=60°,
∴∠EOG=30°,
∴EGr,
∴OGr,
∴正六边形ABCDEF的面积=6rrr2,
∵⊙O的面积=πr2,
∴.
【点睛】本题考查了正多边形与圆,正六边形的性质,勾股定理,正确的作出辅助线是解题的关键.
【变式9-1】(23-24·湖北武汉·模拟预测)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【答案】(1)见解析;(2)等边△ABC的边心距1.
【分析】(1)由圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,结合∠APC=∠CPB=60°可得∠BAC=∠ABC=60°,即可判断△ABC的形状;
(2)过O作OD⊥BC于D,连接OB,然后根据直角三角形的性质进行计算即可.
【详解】(1)证明:在⊙O中,
∵∠BAC与∠CPB是 对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
【点睛】本题考查了正多边形与圆、圆周角定理、等边三角形的判定与性质,作出辅助线、构造直角三角形以及证明△ABC是等边三角形是解答本题的关键.
【变式9-2】(23-24九年级上·湖北武汉·期中)如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
【答案】(1)见解析
(2)见解析
【分析】(1)证明,即可得出.
(2)连接,过点作交的延长线于.证明,推出,即可解决问题.
【详解】(1)证明:∵四边形是正方形,
∴,
∴.
∵是的中点,
∴,
∴,
∴.
(2)解:连接,过点作交的延长线于.
∵四边形是正方形,
∴.
∵,
∴,
∴.
∵,
∴.
在和中,
,
∴,
∴,
∴,
即.
【点睛】本题考查正多边形与圆,正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,勾股定理,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
【变式9-3】(23-24九年级上·全国·单元测试)如图,已知的内接正十边形,交,于,,求证:
(1);
(2).
【答案】(1)证明见详解
(2)证明见详解
【分析】(1)根据圆心角的计算可得,,由此可得,根据同弧所对圆心角是圆周角的2倍可得,根据三角形内角和可得,根据正十边形的性质,内角和定理可得,由此可得,根据平行线的判定即可求解;
(2)根据(1)的计算,可得,,再根据即可求解.
【详解】(1)证明:如图所示,连接,则,
∵是内接正十边形的边长,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴,
∵内接正十边形,
∴,
∴,
∴,
∴;
(2)证明:由(1)可知,,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题主要考查正多边形与圆的综合,掌握正多形的性质,多边形内角和定理,圆心角的计算,等腰三角形的性质,同弧所对圆心角与圆周角的关系,平行线的判定等知识,图形结合分析是解题的关键.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 求正多边形中心角】 2
【题型2 由正多边形中心角求边数】 3
【题型3 尺规作正多边形】 3
【题型4 正多边形和圆中求线段长度】 5
【题型5 正多边形和圆中求角度】 6
【题型6 正多边形和圆中求周长】 7
【题型7 正多边形和圆中求面积】 8
【题型8 正多边形和圆中求最值】 9
【题型9 正多边形和圆中的证明】 10
知识点:正多边形和圆
(1)正多边形的有关概念
正多边形与圆的关系非常密切,把圆分成n(n就是大于2的自然数)等份,顺次连接各分点所的的多边形就是这个圆的内接正多边形,这个圆就就是这个正多边形的外接圆。
正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心。
正多边形的半径:外接圆的半径叫做正多边形的半径。
正多边形的中心角:正多边形每一条边所对的圆心角叫做正多边形的中心角。
正多边形的边心距:中心到正多边形一边的距离叫做正多边形的边心距。
(2)正多边形的有关计算
中心角 边心距 周长 面积
为边数;为边心距;为半径;为边长
(3)正多边形每个内角度数为,每个外角度数为
【题型1 求正多边形中心角】
【例1】(23-24九年级上·江苏南京·期中)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
【变式1-1】(23-24九年级上·江苏泰州·期末)将一个正八边形绕着其中心旋转后与原图形重合,旋转角的大小不可能是( )
A. B. C. D.
【变式1-2】(23-24九年级下·安徽淮北·阶段练习)苯(分子式为)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2是其平面示意图,点O为正六边形的中心,则的度数为( )
A. B. C. D.
【变式1-3】(15-16九年级上·江苏镇江·阶段练习)如图,在正十边形中,连接、,则 °
【题型2 由正多边形中心角求边数】
【例2】(23-24九年级上·江苏盐城·期中)如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
【变式2-1】(23-24九年级下·江苏苏州·阶段练习)已知一个正多边形的中心角为,边长为5,那么这个正多边形的周长等于 .
【变式2-2】(23-24九年级上·江苏泰州·期末)如图,四边形是的内接四边形,是的内接正边形的一边,是的内接正边形的一边,,则 .
【变式2-3】(23-24九年级上·江苏宿迁·期末)如图,AC是⊙O的内接正四边形的一边,点B在弧AC上,且BC是⊙O的内接正六边形的一边.若AB是⊙O的内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
【题型3 尺规作正多边形】
【例3】(23-24九年级上·福建福州·期中)尺规作图:如图,AD为⊙O的直径。
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
【变式3-1】(23-24·陕西·一模)如图,已知,请用尺规作图法求作的内接正方形.(保留作图痕迹,不写作法)
【变式3-2】(23-24九年级·河北·专题练习)如图,在⊙O中,MF为直径,OA⊥MF,圆内接正五边形ABCDE的部分尺规作图步骤如下:
①作出半径OF的中点H.
②以点H为圆心,HA为半径作圆弧,交直径MF于点G.
③AG长即为正五边形的边长、依次作出各等分点B,C,D,E.
已知⊙O的半径R=2,则AB2= .(结果保留根号)
【变式3-3】(2024·江苏无锡·一模)尺规作图:
(1)请在图①中以矩形的边为边作菱形,使得点E在上;
(2)请在图②中以矩形的边为直径作,并在上确定点P,使得的面积与矩形的面积相等.
【题型4 正多边形和圆中求线段长度】
【例4】(23-24九年级上·河北石家庄·期中)如图,半径为2的是正六边形的外接圆,则边心距的长度为( )
A.1 B. C. D.2
【变式4-1】(23-24九年级上·江苏南京·期中)如图,六边形ABCDEF是⊙O的内接正六边形,分别以点A、D为圆心,AE长为半径作弧,在⊙O外交于点G,连接OG.若⊙O的半径为1,则OG的长度为 .
【变式4-2】(23-24九年级·全国·假期作业)如图,正方形和正三角形内接于,、交于、,若正方形的边长是4,则的长度为
A. B. C. D.
【变式4-3】(23-24九年级上·浙江绍兴·阶段练习)如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
【题型5 正多边形和圆中求角度】
【例5】(23-24九年级上·广东东莞·期末)如图,正六边形内接于,边长为2.
(1)求的直径的长;
(2)求的度数.
【变式5-1】(2024·宁夏银川·二模)如图,正五边形内接于,P为劣弧上的动点,则的大小为 .
【变式5-2】(23-24九年级上·全国·单元测试)如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
【变式5-3】(2024·安徽淮北·二模)如图,是正五边形和正六边形的外接圆,连接和,则的度数为 .
【题型6 正多边形和圆中求周长】
【例6】(2024九年级上·江苏·专题练习)如图,是正六边形的外接圆,若的半径为6,则四边形的周长是( )
A. B. C. D.
【变式6-1】(23-24九年级上·浙江温州·期中)如图,六边形是的内接正六边形,记的周长为,正六边形的周长为,则的值为 .
【变式6-2】(23-24九年级上·河南许昌·期末)如图,正六边形内接于,已知的半径为1,连接,则四边形的周长为( )
A.6 B. C.4 D.
【变式6-3】(23-24九年级上·江苏无锡·期中)如图,正方形内接于⊙O,线段在对角线上运动,若⊙O的周长为,,则周长的最小值是 .
【题型7 正多边形和圆中求面积】
【例7】(2024·江苏南京·三模)如图,表示中去掉内接正三角形部分的面积,表示中去掉内接正六边形部分的面积,和的半径均为,则 .(填“、或”)
【变式7-1】(23-24九年级上·全国·课后作业)如图,的半径为,以的内接正八边形的一边为边在内作正方形,则正方形的面积为 .
【变式7-2】(2024·江苏无锡·一模)魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积. 如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.1 B. C.3 D.4
【变式7-3】(23-24九年级上·安徽芜湖·阶段练习)如图,的半径为,是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
【题型8 正多边形和圆中求最值】
【例8】(23-24九年级上·山东临沂·期末)如图,的圆心与正方形的中心重合,已知的半径和正方形的边长都为2,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.1 C. D.
【变式8-1】(23-24·陕西西安·一模)如图,点P为⊙上一点,连接OP,且,点A为OP上一动点,点B为⊙上一动点,连接AB,以线段AB为边在⊙内构造矩形ABCD,且点C在⊙上,则矩形ABCD面积的最大值为 .
【变式8-2】(23-24九年级上·内蒙古鄂尔多斯·期末)如图,点是边长为2的正六边形内的一点(不包括边界),且,是上的一点,是的中点,则的最小值为 .
【变式8-3】(23-24·广东广州·中考真题)如图,为等边的外接圆,半径为2,点在劣弧上运动(不与点重合),连接,,.
(1)求证:是的平分线;
(2)四边形的面积是线段的长的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置,的周长有最小值,随着点的运动,的值会发生变化,求所有值中的最大值.
【题型9 正多边形和圆中的证明】
【例9】(23-24九年级上·浙江·期末)如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
【变式9-1】(23-24·湖北武汉·模拟预测)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【变式9-2】(23-24九年级上·湖北武汉·期中)如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
【变式9-3】(23-24九年级上·全国·单元测试)如图,已知的内接正十边形,交,于,,求证:
(1);
(2).21世纪教育网(www.21cnjy.com)
专题24.8 正多边形与圆【九大题型】
【人教版】
【题型1 求正多边形中心角】 2
【题型2 由正多边形中心角求边数】 5
【题型3 尺规作正多边形】 8
【题型4 正多边形和圆中求线段长度】 13
【题型5 正多边形和圆中求角度】 18
【题型6 正多边形和圆中求周长】 21
【题型7 正多边形和圆中求面积】 25
【题型8 正多边形和圆中求最值】 29
【题型9 正多边形和圆中的证明】 35
知识点:正多边形和圆
(1)正多边形的有关概念
正多边形与圆的关系非常密切,把圆分成n(n就是大于2的自然数)等份,顺次连接各分点所的的多边形就是这个圆的内接正多边形,这个圆就就是这个正多边形的外接圆。
正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心。
正多边形的半径:外接圆的半径叫做正多边形的半径。
正多边形的中心角:正多边形每一条边所对的圆心角叫做正多边形的中心角。
正多边形的边心距:中心到正多边形一边的距离叫做正多边形的边心距。
(2)正多边形的有关计算
中心角 边心距 周长 面积
为边数;为边心距;为半径;为边长
(3)正多边形每个内角度数为,每个外角度数为
【题型1 求正多边形中心角】
【例1】(23-24九年级上·江苏南京·期中)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
【答案】C
【分析】本题考查了正多边形与圆,圆周角定理,三角形外角的性质,添加辅助线是解题的关键.根据正多边形与圆求出相应的圆心角度数,再根据圆周角定理和三角形外角的性质可得答案.
【详解】解:如图,设这个正九边形的外接圆为,
则,
∴,
∴,
故选:C.
【变式1-1】(23-24九年级上·江苏泰州·期末)将一个正八边形绕着其中心旋转后与原图形重合,旋转角的大小不可能是( )
A. B. C. D.
【答案】B
【分析】本题考查了正多边形的性质,解题的关键是掌握正多边形中心角的度数为,先求出正八边形中心角的度数,即可解答.
【详解】解:正八边形的中心角为,
∵,
∴旋转角的大小可能是,,,
∵不是的整数倍,
∴旋转角的大小不能是,
故选:B.
【变式1-2】(23-24九年级下·安徽淮北·阶段练习)苯(分子式为)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2是其平面示意图,点O为正六边形的中心,则的度数为( )
A. B. C. D.
【答案】A
【分析】根据点O为正六边形的中心,得到,,继而得到,,解答即可.
本题考查了正多边形的性质,中心角的计算,等腰三角形的三线合一性质,熟练掌握多边形的性质和中心角的计算是解题的关键.
【详解】∵点O为正六边形的中心,
∴,
∴,
∴,
∴,
故选:A.
【变式1-3】(15-16九年级上·江苏镇江·阶段练习)如图,在正十边形中,连接、,则 °
【答案】54
【分析】设正十边形的圆心O,连接A7O、A4O,再求出∠A7OA4,最后运用圆周角定理解答即可.
【详解】解:如图:设正十边形的圆心O,连接A7O、A4O,
∵正十边形的各边都相等
∴∠A7OA4=×360°=108°
∴108°×=54°.
故填54.
【点睛】本题主要考查了正多边形和圆以及圆周角定理,根据题意正确作出辅助线、构造出圆周角是解答本题的关键.
【题型2 由正多边形中心角求边数】
【例2】(23-24九年级上·江苏盐城·期中)如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
【答案】A
【分析】作正多边形的外接圆,根据圆周角定理得到,根据中心角的定义即可求解.
【详解】解:如图,作正多边形的外接圆,
∵,
∴,
∴这个正多边形的边数为.
故选:A.
【点睛】此题主要考查正多边形的性质,解题的关键是熟知圆周角定理.
【变式2-1】(23-24九年级下·江苏苏州·阶段练习)已知一个正多边形的中心角为,边长为5,那么这个正多边形的周长等于 .
【答案】40
【分析】利用正多边形的中心角求出正多边形的边数,最后根据正多边形的性质求出其周长.
【详解】解:一个正多边形的中心角为,
这个正多边形的边数为:,
这个正多边形的周长为:.
故答案为:40.
【点睛】本题主要考查了正多边形的性质,解题的关键在于知道中心角与边长的关系.
【变式2-2】(23-24九年级上·江苏泰州·期末)如图,四边形是的内接四边形,是的内接正边形的一边,是的内接正边形的一边,,则 .
【答案】48或36
【分析】本题考查了正多边形与圆:把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆;熟练掌握正多边形的有关概念.连接,如图,利用正多边形与圆,分别计算的内接正m边形与内接正n边形的中心角得到,根据,得到m,n的值,然后代入计算即可.
【详解】解:连接,如图,
,
,
,
,
,
m,n的中有一个值必是3的倍数,且均为正整数,
设(均为正整数),则,
(n为正整数),
当时,(不符合题意);
当时,,则;
当时,(不符合题意);
当时,,则;
当时,(不符合题意);
当时,,(不符合题意);
;
当时,n均不为正整数,(不符合题意);
综上,的值为48或36.
【变式2-3】(23-24九年级上·江苏宿迁·期末)如图,AC是⊙O的内接正四边形的一边,点B在弧AC上,且BC是⊙O的内接正六边形的一边.若AB是⊙O的内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
【答案】D
【分析】连接AO、BO、CO,根据中心角度数=360°÷边数n,分别计算出∠AOC、∠BOC的度数,根据角的和差则有∠AOB=30°,根据边数n=360°÷中心角度数即可求解.
【详解】连接AO、BO、CO,
∵AC是⊙O内接正四边形的一边,
∴∠AOC=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠BOC=360°÷6=60°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故选:D.
【点睛】本题考查正多边形和圆,解题的关键是根据正方形的性质、正六边形的性质求出中心角的度数.
【题型3 尺规作正多边形】
【例3】(23-24九年级上·福建福州·期中)尺规作图:如图,AD为⊙O的直径。
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
【答案】(1)见解析;(2)4
【分析】(1)如图,在⊙O上依次截取六段弦,使它们都等于OA,从而得到正六边形ABCDEF;
(2)连接OF,可得△OFE是等边三角形,边长为4,可求得∠OEF=60°,∠DFE=30°,设BE与DF交于G点,可得∠FGE=90°,即可求得FG的长,进而求得FD的长.
【详解】(1)如图,正六边形ABCDEF为所作;
(2)连接OF,设BE与DF交于G点
∵六边形ABCDEF为正六边形
∴∠FOE=60°,DF=DE,∠DEF=120°
∴∠DFE=30°
∵OE=OF
∴△FOE为等边三角形
∴EF=OE=4,∠OEF=60°
∴∠FGE=90°
∴EG=OE=2
∴FG=
∴FD=2FG=
【点睛】此题主要考查了复杂作图及正多边形的计算,关键是掌握圆的内接正六边形的边长等于圆的半径.
【变式3-1】(23-24·陕西·一模)如图,已知,请用尺规作图法求作的内接正方形.(保留作图痕迹,不写作法)
【答案】见解析
【分析】本题考查了作正方形,考查了圆的基本性质,正方形的判定;先在圆上确定一点,连接并延长交于点,再作的垂直平分线交于B、D,连接,则四边形就是所求作的内接正方形.
【详解】解:如图,正方形为所作.
垂直平分,为的直径,
为的直径,
,
,,,
四边形是矩形
,
四边形是正方形,
又都在圆上,
四边形是的内接正方形.
【变式3-2】(23-24九年级·河北·专题练习)如图,在⊙O中,MF为直径,OA⊥MF,圆内接正五边形ABCDE的部分尺规作图步骤如下:
①作出半径OF的中点H.
②以点H为圆心,HA为半径作圆弧,交直径MF于点G.
③AG长即为正五边形的边长、依次作出各等分点B,C,D,E.
已知⊙O的半径R=2,则AB2= .(结果保留根号)
【答案】
【分析】连接AG,由作图可知,OA=2,H为OF中点,可求OH=,由勾股定理得AH=,可求OG=﹣1,由勾股定理AB2=AG2=OA2+OG2=4+(﹣1)2=10﹣2即可.
【详解】解:连接AG,由作图可知,OA=2,OH=1,H为OF中点,
∴OH=,
在Rt△OAH中,由勾股定理
∴AH=,
∵AH=HG=,
∴OG=GH﹣OH=﹣1,
在Rt△AOG中,由勾股定理得,
∴AB2=AG2=OA2+OG2=4+(﹣1)2=10﹣2.
故答案为:10﹣2.
【点睛】本题考查尺规作圆内接正五边形的方法与步骤,线段垂直平分线,勾股定理,作圆弧,掌握圆内接正五边形的方法与步骤,线段垂直平分线,勾股定理,作圆弧的方法是解题关键.
【变式3-3】(2024·江苏无锡·一模)尺规作图:
(1)请在图①中以矩形的边为边作菱形,使得点E在上;
(2)请在图②中以矩形的边为直径作,并在上确定点P,使得的面积与矩形的面积相等.
【答案】(1)见解析
(2)见解析
【分析】(1)结合菱形的判定,以点D为圆心,的长为半径画弧,交为点E,再分别以点E、点A为圆心,的长为半径画弧,两弧交于点F,连接、、即可;
(2)作线段的垂直平分线,交于点O,以点O为圆心,的长为半径画圆,即可得,以点O为圆心,的长为半径画弧,在的上方交于点E,再作,作直线,分别交于点、,即可求解.
【详解】(1)解:如图,菱形即为所求,
(2)解:如图,点、即为所求,
【点睛】本题考查作图 复杂作图、菱形的判定、矩形的性质、垂直平分线的性质,理解题意、灵活运用相关知识是解题的关键.
【题型4 正多边形和圆中求线段长度】
【例4】(23-24九年级上·河北石家庄·期中)如图,半径为2的是正六边形的外接圆,则边心距的长度为( )
A.1 B. C. D.2
【答案】B
【分析】如图所示,连接,求出,进而证明是等边三角形,得到,求出,即可利用勾股定理求出答案.
【详解】解:如图所示,连接,
由题意得,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,
故选B.
【点睛】本题主要考查了正多边形与圆,勾股定理,等边三角形的性质与判断,正确作出辅助线构造直角三角形是解题的关键.
【变式4-1】(23-24九年级上·江苏南京·期中)如图,六边形ABCDEF是⊙O的内接正六边形,分别以点A、D为圆心,AE长为半径作弧,在⊙O外交于点G,连接OG.若⊙O的半径为1,则OG的长度为 .
【答案】
【分析】连接AG,AD,AE,OE,过点O作OH⊥AE于点H,解直角三角形求出AE,再利用勾股定理求出OG即可.
【详解】解:如图,连接AG,AD,AE,OE,过点O作OH⊥AE于点H.
∵OH⊥AE,
∴AH=EH,
∵∠AOE=120°,
∴∠OAE=∠OEA=30°,
OH=OA=,AH=,
∴,
∴,
在和中
∴
∴
∴
故答案为:.
【点睛】此题考查了圆的性质,全等三角形的判定,勾股定理,解题的关键是熟练掌握相关基本性质.
【变式4-2】(23-24九年级·全国·假期作业)如图,正方形和正三角形内接于,、交于、,若正方形的边长是4,则的长度为
A. B. C. D.
【答案】A
【分析】连接交于,连接,根据正方形的性质、等边三角形的性质及等腰三角形的性质即可求解.
【详解】解:连接交于,连接,
四边形是正方形,
,
是的直径,
是等腰直角三角形,
,
,
是等边三角形,
,,
,
,
,,
,
是等腰直角三角形,
.
故选:.
【点睛】本题考查正多边形与圆的关系,涉及到特殊锐角三角函数值、正方形的性质、等边三角形的性质及等腰三角形的性质,解题的关键是综合运用所学知识.
【变式4-3】(23-24九年级上·浙江绍兴·阶段练习)如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
【答案】(1)
(2)
【分析】(1)连接,,根据正六边形的性质可得,再根据圆的半径都相等可得是等边三角形,进而可求解.
(2)连接,,由为的直径,得,利用勾股定理及中点的性质即可求解.
【详解】(1)解:连接,,如图:
六边形是正六边形,
,
又 ,是的半径,且半径为,
,
是等边三角形,
.
(2)连接,,如图:
则为的直径,
,,
由(1)得:,
在中,,
,
G为的中点,
,
在中,,
.
【点睛】本题考查了正多边形的性质、等边三角形的判定及性质、勾股定理及圆周角,熟练掌握基础知识,借助适当的辅助线解决问题是解题的关键.
【题型5 正多边形和圆中求角度】
【例5】(23-24九年级上·广东东莞·期末)如图,正六边形内接于,边长为2.
(1)求的直径的长;
(2)求的度数.
【答案】(1)
(2)
【分析】本题考查正多边形和圆,圆周角定理:
(1)连接,求出的度数,得到是等边三角形,得到,即可得出结果;
(2)根据圆周角定理,即可得出结果.
【详解】(1)解:连接.
∵正六边形内接于,
∴,
又,
∴是等边三角形.
∴.
∴.
(2)解:∵,
∴.
【变式5-1】(2024·宁夏银川·二模)如图,正五边形内接于,P为劣弧上的动点,则的大小为 .
【答案】/144度
【分析】本题考查了正多边形和圆,圆内接四边形的性质,作出圆中常用辅助线是解题的关键.连接,正多边形的性质得的度数,由圆周角定理得的度数,再圆内接四边形的性质即可求解.
【详解】解:如图,连接,
∵五边形是正五边形,
∴,
∵,
∴,
∵正五边形的外接圆为,
∴四边形是内接四边形,
∴,
∴;
故答案为:.
【变式5-2】(23-24九年级上·全国·单元测试)如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
【答案】
【分析】本题考查的是正多边形和圆、圆周角定理的应用,连接、、,根据正多边形和圆的知识求出正八边形的中心角的度数,根据圆周角定理求出的度数.
【详解】解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
【变式5-3】(2024·安徽淮北·二模)如图,是正五边形和正六边形的外接圆,连接和,则的度数为 .
【答案】/24度
【分析】本题考查正多边形与圆,连接,根据正多边形的性质可得:,进而得到,,再根据即可求解.
【详解】解:连接,
根据题意得:,
,
,
,
故答案为:.
【题型6 正多边形和圆中求周长】
【例6】(2024九年级上·江苏·专题练习)如图,是正六边形的外接圆,若的半径为6,则四边形的周长是( )
A. B. C. D.
【答案】C
【分析】本题考查正多边形和圆,矩形,掌握正六边形的性质,矩形的性质以及直角三角形的边角关系是正确解答的关键.根据正六边形的性质,矩形的性质以及直角三角形的边角关系求出,即可.
【详解】解:如图,连接,,,过点作于点,则,
点是正六边形的中心,
,
,
是正三角形,
,
在中,,,
,
,
四边形的周长是,
故选:C
【变式6-1】(23-24九年级上·浙江温州·期中)如图,六边形是的内接正六边形,记的周长为,正六边形的周长为,则的值为 .
【答案】
【分析】本题主要考查了正六边形的性质,含30°角的直角三角形的性质,设正六边形的边长为a,利用含角的直角三角形的性质求出,从而得出的长,进而解决问题.
【详解】解:设正六边形的边长为a,
连接,交于H,如下图:
∵六边形是的内接正六边形,
∴,,,
∴
∴,
∴
∴,
由正六边形的性质知,是等边三角形,
∴,
故答案为:.
【变式6-2】(23-24九年级上·河南许昌·期末)如图,正六边形内接于,已知的半径为1,连接,则四边形的周长为( )
A.6 B. C.4 D.
【答案】C
【分析】本题考查的是正多边形和圆,连接,则, 均为等边三角形.所以.即得出四边形的周长.熟知正六边形的性质是解答此题的关键.
【详解】解:连接,如解图所示.
六边形是正六边形,
.
又,
, 均为等边三角形.
.
四边形的周长为,
故选:.
【变式6-3】(23-24九年级上·江苏无锡·期中)如图,正方形内接于⊙O,线段在对角线上运动,若⊙O的周长为,,则周长的最小值是 .
【答案】/
【分析】过点作,令;可推出四边形为平行四边形,有;根据可知当时,周长有最小值.
【详解】解:过点作,令
∵⊙O的周长为,
∴⊙O的半径为
∴
∵且
∴四边形为平行四边形
∴
由正方形的对称性可得:
∴
∴
故:当时,周长有最小值
此时:
∴周长的最小值是
故答案为:
【点睛】本题考查了正方形的性质、平行四边形的判定与性质等.推出当时,周长有最小值是解题关键.
【题型7 正多边形和圆中求面积】
【例7】(2024·江苏南京·三模)如图,表示中去掉内接正三角形部分的面积,表示中去掉内接正六边形部分的面积,和的半径均为,则 .(填“、或”)
【答案】
【分析】本题考查了圆的内接正多边形,分别求出、,再根据作差法即可求解,掌握圆的内接正多边形的性质是解题的关键.
【详解】解:如图,连接,过作于,连接,过作于,
在图中,,,,,
∴,,
∴,
∴
,
在图中,,,
∴为等边三角形,
∵,
∴,
∴,
∴,
,
∴,
∴,
∴,
故答案为:.
【变式7-1】(23-24九年级上·全国·课后作业)如图,的半径为,以的内接正八边形的一边为边在内作正方形,则正方形的面积为 .
【答案】
【分析】本题考查了正多边形和圆,等腰直角三角形的判定和性质,勾股定理;
连接,,过A作于E,求出,可得是等腰直角三角形,然后求出,进而求出,然后利用勾股定理求出即可得到答案.
【详解】解:如图,连接,,过A作于E,则,
∵是正八边形的中心角,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
∴正方形的面积为:,
故答案为:.
【变式7-2】(2024·江苏无锡·一模)魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积. 如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.1 B. C.3 D.4
【答案】C
【分析】本题考查了正多边形与圆,三角形的面积的计算,解直角三角形,正确的作出辅助线是解题的关键.过作于,得到圆的内接正十二边形的圆心角为,根据三角形的面积公式即可得到结论.
【详解】解:如图,过作于,
圆的内接正十二边形的圆心角为,
,
,
,
这个圆的内接正十二边形的面积为,
故选:C
【变式7-3】(23-24九年级上·安徽芜湖·阶段练习)如图,的半径为,是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
【答案】A
【分析】连接、,根据平行四边形的性质得,再根据圆周角定理得为的直径,利用圆周角定理得到,根据含的直角三角形三边的关系得到,然后根据矩形的面积公式求解.
【详解】解:连接、,如图,
四边形为平行四边形,
,
,
,
为的直径,
,
为等边三角形,
,
,
而,
,
在中,,,
矩形的面积.
故选:A.
【点睛】本题考查了三角形外接圆与外心,垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、等边三角形的性质和矩形的性质,综合运用以上知识是解题的关键.
【题型8 正多边形和圆中求最值】
【例8】(23-24九年级上·山东临沂·期末)如图,的圆心与正方形的中心重合,已知的半径和正方形的边长都为2,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.1 C. D.
【答案】D
【分析】此题考查了圆与正多边形的性质,勾股定理,设正方形四个顶点分别为,连接并延长,交于点,由题意可得,的长度为圆上任意一点到正方形边上任意一点距离的最小值,求解即可.
【详解】解:设正方形四个顶点分别为,连接并延长,交于点,过点作,如下图:
则的长度为圆上任意一点到正方形边上任意一点距离的最小值,
由题意可得:,,
由勾股定理可得:,
∴,
故选:D.
【变式8-1】(23-24·陕西西安·一模)如图,点P为⊙上一点,连接OP,且,点A为OP上一动点,点B为⊙上一动点,连接AB,以线段AB为边在⊙内构造矩形ABCD,且点C在⊙上,则矩形ABCD面积的最大值为 .
【答案】32
【分析】根据当圆的半径确定以后,圆内接正方形是圆内接矩形中面积最大的,进而求得圆内接正方形的面积,则矩形ABCD面积的最大值为圆内接正方形面积,据此求解即可.
【详解】如图,四边形BCEF是圆O的内接正方形,当圆的半径确定以后,圆内接正方形是圆内接矩形中面积最大的;
点A,D分别是正方形的对边BF,CE的中点,
此时矩形ABCD的面积恰好是正方形BCEF的面积,
圆O的直径PQ恰好经过点A,D,
连接BE ,
四边形BCEF是圆O的内接正方形,OP=4,
BE = PQ = 2OP =8,BC = CE,
∠C= 90°,
BC2 + CE2 = 2BO2 = BE2 = 8,
BC2=32,即S正方形BCEF=32,
如图,当重合时,当四点都在圆上时,四边形是正方形
矩形ABCD面积的最大值为32.
故答案为:32.
【点睛】本题考查了圆内接四边形,将问题转化为圆内接四边形是解题的关键.
【变式8-2】(23-24九年级上·内蒙古鄂尔多斯·期末)如图,点是边长为2的正六边形内的一点(不包括边界),且,是上的一点,是的中点,则的最小值为 .
【答案】2
【分析】本题考查了正多边形,轴对称的性质,等边三角形的判定与性质,直角三角形斜边中线的性质等知识.取中点O,中点,连接,,延长、相交于点T,利用轴对称的性质可得,从而得出当共线时,的最小值为,然后利用直角三角形斜边中线的性质求出,证明,为等边三角形,即可求解.
【详解】解:取中点O,中点,连接,,延长、相交于点T,
,
∵正六边形关于直线对称,
∴,也关于直线对称,
∴,
∵,O为中点,
∴,
∴,
当共线时,,
∴的最小值为,
∵正六边形的边长为2,
∴,,
∴是等边三角形,
∴,,
∵,O为中点,Q为中点,
∴,,
∴,
∴是等边三角形,
∴,
∴,
∴的最小值为2.
故答案为:2.
【变式8-3】(23-24·广东广州·中考真题)如图,为等边的外接圆,半径为2,点在劣弧上运动(不与点重合),连接,,.
(1)求证:是的平分线;
(2)四边形的面积是线段的长的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置,的周长有最小值,随着点的运动,的值会发生变化,求所有值中的最大值.
【答案】(1)详见解析;(2)是, ;(3)
【分析】(1)根据等弧对等角的性质证明即可;
(2)延长DA到E,让AE=DB,证明△EAC≌△DBC,即可表示出S的面积;
(3)作点D关于直线BC、AC的对称点D1、D2,当D1、M、N、D共线时△DMN取最小值,可得t=D1D2,有对称性推出在等腰△D1CD2中,t=,D与O、C共线时t取最大值即可算出.
【详解】(1)∵△ABC为等边三角形,BC=AC,
∴ ,都为圆,
∴∠AOC=∠BOC=120°,
∴∠ADC=∠BDC=60°,
∴DC是∠ADB的角平分线.
(2)是.
如图,延长DA至点E,使得AE=DB.
连接EC,则∠EAC=180°-∠DAC=∠DBC.
∵AE=DB,∠EAC=∠DBC,AC=BC,
∴△EAC≌△DBC(SAS),
∴∠E=∠CDB=∠ADC=60°,
故△EDC是等边三角形,
∵DC=x,∴根据等边三角形的特殊性可知DC边上的高为
∴.
(3)依次作点D关于直线BC、AC的对称点D1、D2,根据对称性
C△DMN=DM+MN+ND=D1M+MN+ND2.
∴D1、M、N、D共线时△DMN取最小值t,此时t=D1D2,
由对称有D1C=DC=D2C=x,∠D1CB=∠DCB,∠D2CA=∠DCA,
∴∠D1CD2=∠D1CB+∠BCA+∠D2CA=∠DCB+60°+∠DCA=120°.
∴∠CD1D2=∠CD2D1=60°,
在等腰△D1CD2中,作CH⊥D1D2,
则在Rt△D1CH中,根据30°特殊直角三角形的比例可得D1H=,
同理D2H=
∴t=D1D2=.
∴x取最大值时,t取最大值.
即D与O、C共线时t取最大值,x=4.
所有t值中的最大值为.
【点睛】本题考查圆与正多边形的综合以及动点问题,关键在于结合题意作出合理的辅助线转移已知量.
【题型9 正多边形和圆中的证明】
【例9】(23-24九年级上·浙江·期末)如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
【答案】(1)证明见解析
(2)
【分析】(1)如图,连接AE,AD,AC,根据正六边形的性质得到EF=ED=CD=BC,求得,于是得到∠FAE=∠EAD=∠DAC=∠CAB,即可得到结论;
(2)如图,过O作OG⊥DE于G,连接OE,设⊙O的半径为r,推出△ODE是等边三角形,得到DE=OD=r,∠OED=60°,根据勾股定理得到OGr,根据三角形和圆的面积公式即可得到结论.
【详解】(1)证明:如图,连接AE,AD,AC,
∵六边形ABCDEF是⊙O的内接正六边形,
∴EF=ED=CD=BC,
∴,
∴∠FAE=∠EAD=∠DAC=∠CAB,
∴过顶点A的三条对角线四等分∠BAF;
(2)解:如图,过O作OG⊥DE于G,连接OE,
设⊙O的半径为r,
∵∠DOE60°,OD=OE=r,
∴△ODE是等边三角形,
∴DE=OD=r,∠OED=60°,
∴∠EOG=30°,
∴EGr,
∴OGr,
∴正六边形ABCDEF的面积=6rrr2,
∵⊙O的面积=πr2,
∴.
【点睛】本题考查了正多边形与圆,正六边形的性质,勾股定理,正确的作出辅助线是解题的关键.
【变式9-1】(23-24·湖北武汉·模拟预测)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【答案】(1)见解析;(2)等边△ABC的边心距1.
【分析】(1)由圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,结合∠APC=∠CPB=60°可得∠BAC=∠ABC=60°,即可判断△ABC的形状;
(2)过O作OD⊥BC于D,连接OB,然后根据直角三角形的性质进行计算即可.
【详解】(1)证明:在⊙O中,
∵∠BAC与∠CPB是 对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
【点睛】本题考查了正多边形与圆、圆周角定理、等边三角形的判定与性质,作出辅助线、构造直角三角形以及证明△ABC是等边三角形是解答本题的关键.
【变式9-2】(23-24九年级上·湖北武汉·期中)如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
【答案】(1)见解析
(2)见解析
【分析】(1)证明,即可得出.
(2)连接,过点作交的延长线于.证明,推出,即可解决问题.
【详解】(1)证明:∵四边形是正方形,
∴,
∴.
∵是的中点,
∴,
∴,
∴.
(2)解:连接,过点作交的延长线于.
∵四边形是正方形,
∴.
∵,
∴,
∴.
∵,
∴.
在和中,
,
∴,
∴,
∴,
即.
【点睛】本题考查正多边形与圆,正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,勾股定理,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
【变式9-3】(23-24九年级上·全国·单元测试)如图,已知的内接正十边形,交,于,,求证:
(1);
(2).
【答案】(1)证明见详解
(2)证明见详解
【分析】(1)根据圆心角的计算可得,,由此可得,根据同弧所对圆心角是圆周角的2倍可得,根据三角形内角和可得,根据正十边形的性质,内角和定理可得,由此可得,根据平行线的判定即可求解;
(2)根据(1)的计算,可得,,再根据即可求解.
【详解】(1)证明:如图所示,连接,则,
∵是内接正十边形的边长,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴,
∵内接正十边形,
∴,
∴,
∴,
∴;
(2)证明:由(1)可知,,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题主要考查正多边形与圆的综合,掌握正多形的性质,多边形内角和定理,圆心角的计算,等腰三角形的性质,同弧所对圆心角与圆周角的关系,平行线的判定等知识,图形结合分析是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
