人教版2024-2025九年级数学上册同步讲义专题专题24.6切线的判定与性质【十大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025九年级数学上册同步讲义专题专题24.6切线的判定与性质【十大题型】(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 00:00:00 | ||
图片预览



文档简介
专题24.6 切线的判定与性质【十大题型】
【人教版】
【题型1 添加条件使直线为切线】 1
【题型2 连半径证垂直证明是切线】 2
【题型3 作垂直证半径证明是切线】 4
【题型4 由切线的性质求线段长度】 5
【题型5 由切线的性质求角度】 6
【题型6 利用切线的性质进行证明】 7
【题型7 作圆的切线】 9
【题型8 利用切线的判定与性质判断结论正误】 10
【题型9 利用切线的判定与性质进行求值或证明】 11
【题型10 切线的应用】 13
知识点:切线的判定与性质
(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线
②和圆只有一个公共点的直线是圆的切线(定义法)
③如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
(2)切线判定常用的证明方法:
①知道直线和圆有公共点时,连半径,证垂直;
②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.
(3)切线的性质:圆的切线垂直于经过切点的半径.
【题型1 添加条件使直线为切线】
【例1】(23-24九年级·河北衡水·阶段练习)如图,是的直径,是上一点,是外一点,过点作,垂足为,连接.若使切于点,添加的下列条件中,不正确的是( )
A. B. C. D.
【变式1-1】(23-24九年级·全国·课后作业)如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
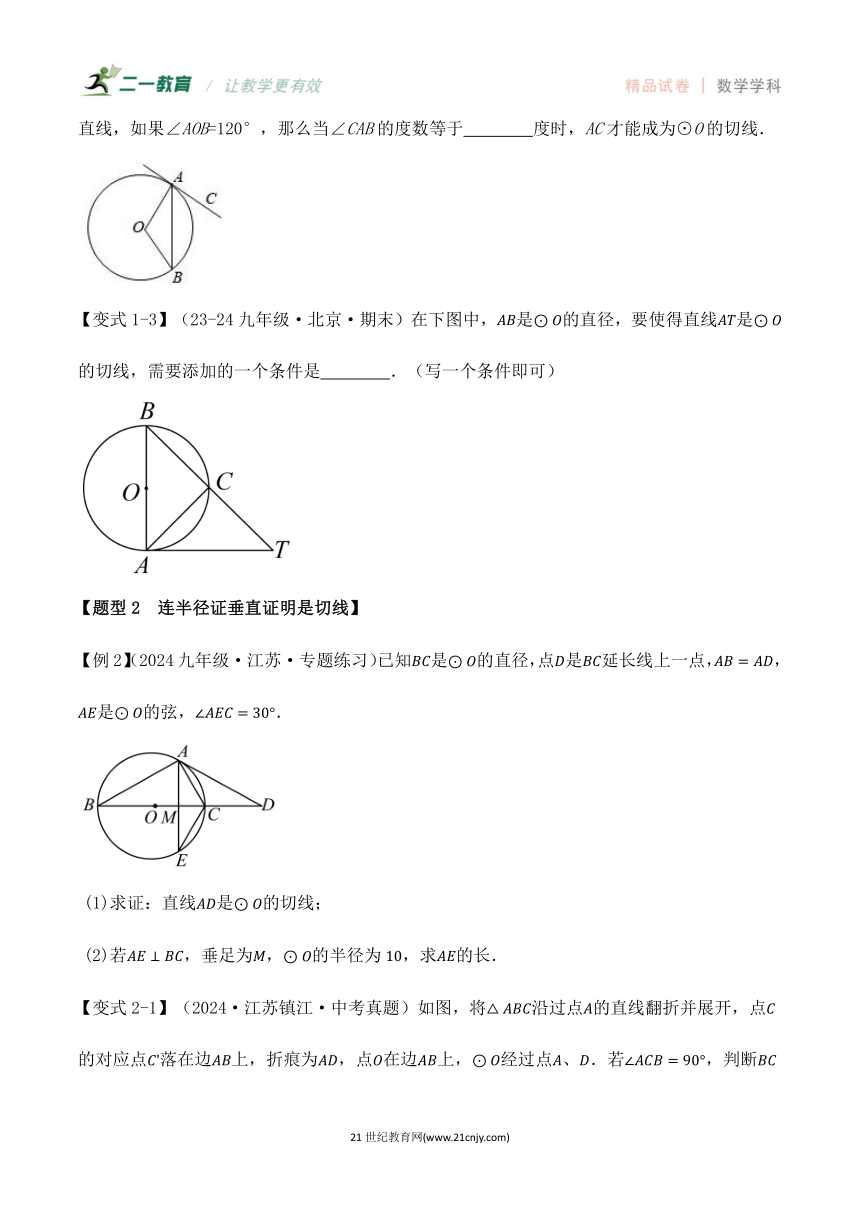
【变式1-2】(23-24九年级·全国·期末)如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
【变式1-3】(23-24九年级·北京·期末)在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
【题型2 连半径证垂直证明是切线】
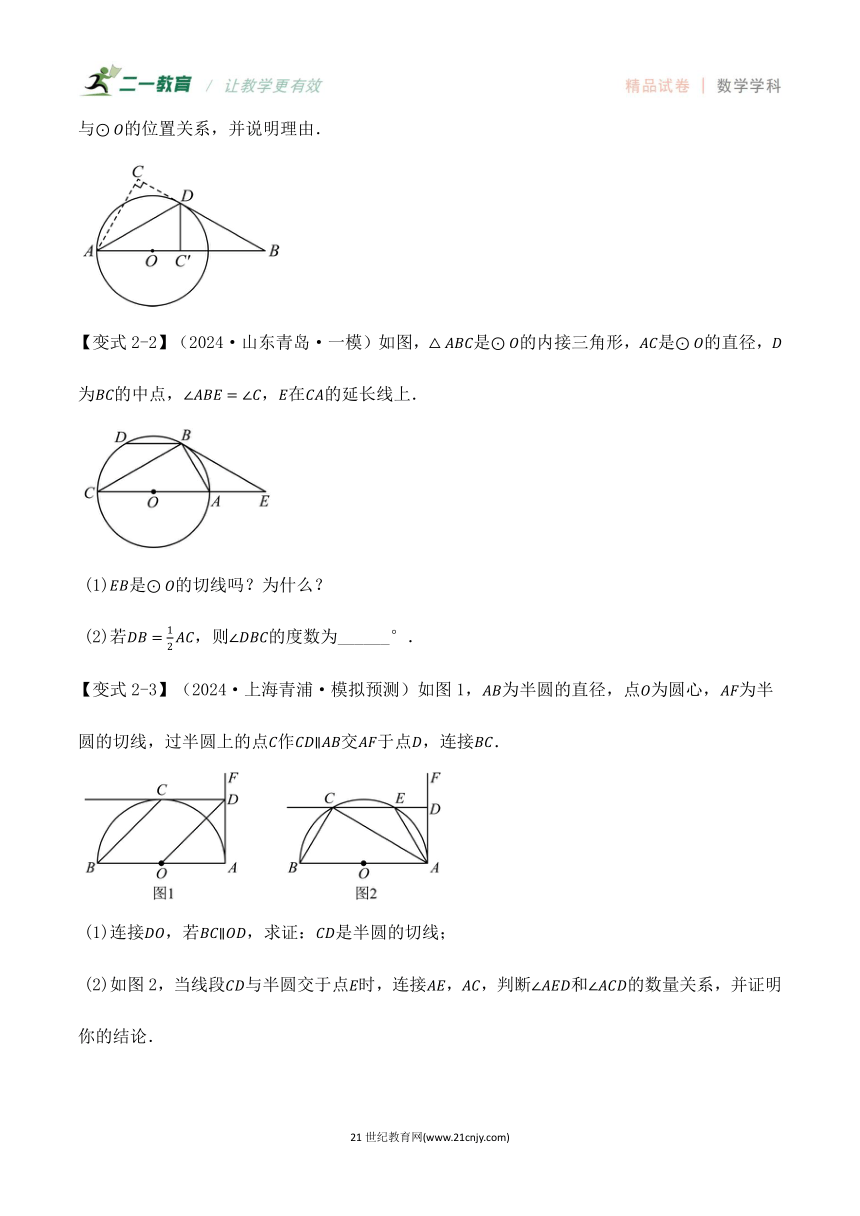
【例2】(2024九年级·江苏·专题练习)已知是的直径,点是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为,的半径为,求的长.
【变式2-1】(2024·江苏镇江·中考真题)如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
【变式2-2】(2024·山东青岛·一模)如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
【变式2-3】(2024·上海青浦·模拟预测)如图1,为半圆的直径,点为圆心,为半圆的切线,过半圆上的点作交于点,连接.
(1)连接,若,求证:是半圆的切线;
(2)如图2,当线段与半圆交于点时,连接,,判断和的数量关系,并证明你的结论.
【题型3 作垂直证半径证明是切线】
【例3】(2024·江苏扬州·中考真题)如图,四边形中,,,,连接,以点B为圆心,长为半径作,交于点E.
(1)试判断与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
【变式3-1】(23-24九年级·广西防城港·期末)如图,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与CD相切于点M,
(1)求证:BC与⊙O相切;
(2)若正方形的边长为1,求⊙O的半径.
【变式3-2】(23-24九年级·山西·期末)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
【变式3-3】(23-24九年级·辽宁大连·期末)如图1,为等腰三角形,是底边的中点,腰与相切于点,底交于点,.
(1)求证:是的切线;
(2)如图2,连接,交于点,点是弧的中点,若,,求的半径.
【题型4 由切线的性质求线段长度】
【例4】(23-24九年级·重庆忠县·期中)如图,是的内接三角形,.点是延长线上一点,且与相切于点,若的半径为1,则长为( )
A. B. C. D.3
【变式4-1】(2024九年级·江苏·专题练习)如图,与相切于点A,交于点B,点C在上,且.若,,则的长为 .
【变式4-2】(2024九年级·江苏·专题练习)如图,是⊙O的直径,,与⊙O相切于点A,交⊙O于点D,连接,若,则的长为( )
A.4 B. C.2 D.
【变式4-3】(2024·海南海口·模拟预测)如图,与相切于点,与弦相交于点,,若,,则的长为 .
【题型5 由切线的性质求角度】
【例5】(2024·海南海口·模拟预测)如图,在中,,圆O与交于点D,与相切于点C,,则 .
【变式5-1】(23-24九年级·重庆九龙坡·开学考试)如图,是的直径,,垂足为E,直线与相切于点C,交于点D,直线交的延长线于点P,连接,若,则的度数是( )
A. B. C. D.
【变式5-2】(2024九年级·江苏·专题练习)如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
【变式5-3】(2024九年级·全国·专题练习)如图分别切于A、B、E,,则( )
A. B. C. D.
【题型6 利用切线的性质进行证明】
【例6】(2024·山西大同·三模)如图,以的一边为直径作,点恰好落在上,射线与相切于点.
(1)尺规作图:过点作于点,延长交于点,连接;(保留作图痕迹,标明相应字母,不写作法)
(2)在(1)的条件下证明:.
【变式6-1】(23-24九年级·福建莆田·期中)如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
【变式6-2】(23-24九年级·安徽蚌埠·期末)如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
【变式6-3】(2024·广东梅州·模拟预测)如图,P为外一点,为的切线,切点分别为A、B,直线交于点D、E,交于点C.
(1)求证∶.
(2)若,连接,求证:四边形是菱形.
【题型7 作圆的切线】
【例7】(2024·江苏镇江·一模)如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上.
(1)的周长为______.
(2)请在如图所示的网格中,用无刻度的直尺在上确定一点,使以点为圆心,以为半径的与相切.(保留作图痕迹)
【变式7-1】(23-24九年级·广东广州·期末)如图,直角梯形中,,,.
(1)尺规作出以为直径的圆(保留作图痕迹,不写作法);
(2)判断与的位置关系,并说明理由.
【变式7-2】(2024·吉林长春·模拟预测)如图,在每个小正方形的边长为1的网格中,的顶点A,B,以为直径的半圆的圆心为O,仅用无刻度的直尺在给定网格中完成画图:
(1)请在图1中作出的边上的高;
(2)请在图2中线段上确定一点F,使得;
(3)请在图3中作出的切线.
【变式7-3】(2024·山东德州·中考真题)如图,,点、分别在射线、上,,.
(1)用尺规在图中作一段劣弧,使得它在、两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;
(3)求所得的劣弧与线段、围成的封闭图形的面积.
【题型8 利用切线的判定与性质判断结论正误】
【例8】(2024九年级·安徽·专题练习)如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【变式8-1】(23-24九年级·安徽合肥·期末)为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
【变式8-2】(2014·江苏无锡·中考真题)如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
【变式8-3】(23-24九年级·河北保定·期中)在黑板上有如下内容:“如图,是半圆所在圆的直径,,点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目,下列判断正确的是( )
嘉嘉:若给出,则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且,则可求出的面积.
A.只有嘉嘉的正确 B.只有淇淇的正确
C.嘉嘉和淇淇的都不正确 D.嘉嘉和淇淇的都正确
【题型9 利用切线的判定与性质进行求值或证明】
【例9】(23-24九年级·黑龙江哈尔滨·阶段练习)如图,中,,点在边上,过点且分别与边、相交于、两点,,点为垂足.
(1)求证:直线是的切线;
(2)当是等边三角形,且直线与相切时,直接写出长度为线段长度2倍的所有线段.
【变式9-1】(2024·辽宁沈阳·二模)如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点,且,连接.
(1)求证:是的切线;
(2)若,,求的半径的长.
【变式9-2】(2024·陕西西安·模拟预测)如图,在中,以边上一点O为圆心,为半径作,与相切于点A.作交的延长线于点D,且.
(1)求证:是的切线;
(2)若,,求⊙O的半径.
【变式9-3】(23-24九年级·广东·单元测试)如图1,为直径,与相切于点B,D为上一点,连接,若.
(1)求证:为的切线;
(2)如图2,过点A作交延长线于点E,连接交于点F,若,求的长.
【题型10 切线的应用】
【例10】(2024·福建宁德·二模)综合与实践:
任务一:确定弦的长度.如图2,求所对弦的长度.
任务二:设计甲组扇面.如图3,已知甲组的圆形卡纸直径为.请运用所给工具在中设计与图2相同的扇面,并标出相应数据.
任务三:确定卡纸大小.如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2,扇面形状为扇环,且,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【变式10-1】(23-24九年级·浙江杭州·)图1是一种推磨工具模型,图2是它的示意图,已知,,点A在中轴线上运动,点B在以O为圆心,长为半径的圆上运动,且,如图3,当点B按逆时针方向运动到时,与相切,则 .
【变式10-2】(2024·河北邯郸·模拟预测)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具.图1,图2是某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,是粒子真空室,C、D是两个加速电极,高速飞行的粒子J在A点注入,在粒子真空室内做环形运动,每次经过 时被加速,达到一定的速度在B点引出,粒子注入和引出路径都与相切.已知:,粒子注入路径与夹角,所对的圆心角是.
(1)求的度数;
(2)通过计算,比较与的长度哪个更长;
(3)直接写出粒子J在环形运动过程中,粒子J到的最远距离.(相关数据: )
【变式10-3】(2013·浙江温州·中考真题)一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线切割,如图1所示.图2中的矩形是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则的长分别是 .
21世纪教育网(www.21cnjy.com)
专题24.6 切线的判定与性质【十大题型】
【人教版】
【题型1 添加条件使直线为切线】 2
【题型2 连半径证垂直证明是切线】 5
【题型3 作垂直证半径证明是切线】 10
【题型4 由切线的性质求线段长度】 16
【题型5 由切线的性质求角度】 21
【题型6 利用切线的性质进行证明】 25
【题型7 作圆的切线】 31
【题型8 利用切线的判定与性质判断结论正误】 37
【题型9 利用切线的判定与性质进行求值或证明】 43
【题型10 切线的应用】 51
知识点:切线的判定与性质
(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线
②和圆只有一个公共点的直线是圆的切线(定义法)
③如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
(2)切线判定常用的证明方法:
①知道直线和圆有公共点时,连半径,证垂直;
②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.
(3)切线的性质:圆的切线垂直于经过切点的半径.
【题型1 添加条件使直线为切线】
【例1】(23-24九年级·河北衡水·阶段练习)如图,是的直径,是上一点,是外一点,过点作,垂足为,连接.若使切于点,添加的下列条件中,不正确的是( )
A. B. C. D.
【答案】D
【分析】本题考查切线的证明,涉及圆的切线的判定、平行线的判定与性质、圆的性质等知识,根据选项,逐项判定即可得到答案,熟记圆的切线的判定是解决问题的关键.
【详解】解:A、 ,
,
当时,则,即,根据切线的判定,切于点,该选项正确,不符合题意;
B、 ,
,则,
,
,
当时,则,即,根据切线的判定,切于点,该选项正确,不符合题意;
C、当时,,
,
,
,即,根据切线的判定,切于点,该选项正确,不符合题意;
D、当时,由得到,则是等腰三角形,无法确定,不能得到切于点,该选项不正确,符合题意;
故选:D.
【变式1-1】(23-24九年级·全国·课后作业)如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
【答案】4
【分析】过M作MN⊥OA于点N,此时以MN为半径的圆与OA相切,根据30°角所对直角边为斜边的一半可得OM的长.
【详解】解:如图,过M作MN⊥OA于点N,
∵MN=2cm,,
∴OM=4cm,
则当OM=4cm时,与OA相切.
故答案为4.
【点睛】本题主要考查切线判定,直角三角形中30°角所对直角边为斜边的一半,解此题的关键在于熟练掌握其知识点.
【变式1-2】(23-24九年级·全国·期末)如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
【答案】60
【分析】由已知可求得∠OAB的度数,因为OA⊥AC,AC才能成为⊙O的切线,从而可求得∠CAB的度数.
【详解】解:∵△AOB中,OA=OB,∠AOB=120°,
∴,
∵当OA⊥AC即∠OAC=90°时,AC才能成为⊙O的切线,
∴当∠CAB的度数等于60°,即OA⊥AC时,AC才能成为⊙O的切线.
故答案为:60.
【点睛】本题考查了切线的判定,三角形内角和定理,等腰三角形的性质,掌握切线的判定定理是解答此题的关键.
【变式1-3】(23-24九年级·北京·期末)在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
【答案】∠ABT=∠ATB=45°(答案不唯一)
【分析】根据切线的判定条件,只需要得到∠BAT=90°即可求解,因此只需要添加条件:∠ABT=∠ATB=45°即可.
【详解】解:添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,
∴∠BAT=90°,
又∵AB是圆O的直径,
∴AT是圆O的切线,
故答案为:∠ABT=∠ATB=45°(答案不唯一).
【点睛】本题主要考查了圆切线的判定,三角形内角和定理,熟知圆切线的判定条件是解题的关键.
【题型2 连半径证垂直证明是切线】
【例2】(2024九年级·江苏·专题练习)已知是的直径,点是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为,的半径为,求的长.
【答案】(1)见解析
(2)
【分析】本题主要考查了切线的判定、同弧所对的圆周角相等、等边对等角、圆周角定理、三角形内角和定理、垂径定理、含度角的直角三角形的性质、勾股定理等知识,灵活运用知识点推理证明是解题的关键.
(1)连接,根据同弧所对的圆周角相等得到,由等边对等角得到,利用圆周角定理得到,利用三角形内角和定理,求得,即可证明直线是的切线;
(2)根据垂径定理得到,根据含度角的直角三角形的性质,得到,根据勾股定理计算,由,得出答案即可.
【详解】(1)证明:如图,连接,
∵,
∴,,
∵,
∴,
∴,
∴,
又∵是的半径,
∴直线是的切线;
(2)解:如图,连接,
∵是的直径,,垂足为,的半径为,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴.
【变式2-1】(2024·江苏镇江·中考真题)如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
【答案】与相切,理由见解析
【分析】连接,由等腰三角形的性质得,再由折叠的性质得,进而证明,则,因此,然后由切线的判定即可得出结论.
【详解】解:与相切.
证明:连接.
∵,
∴.
∵图形沿过点A的直线翻折,点C的对应点落在边上,
∴.
∴.
∴.
∴由,得,即.
∴与相切.
【点睛】本题考查直线与圆的位置关系、等腰三角形的性质、折叠的性质以及平行线的判定与性质等知识,熟练掌握切线的判定和折叠的性质是解题的关键.
【变式2-2】(2024·山东青岛·一模)如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
【答案】(1)是的切线,理由见解析;
(2)30
【分析】本题考查切线的判定,等边三角形的判定及性质,圆周角定理,关键是掌握切线的判定方法,圆周角定理.
(1)由圆周角定理得到,由等腰三角形的性质得到,即可证明问题;
(2)连接,得到是等边三角形,得到,由为的中点,得到,由圆周角定理即可求出的度数.
【详解】(1)解:是的切线,理由如下,
连接,
是圆的直径,
,
,
,
,
,
,
,
半径,
是的切线;
(2)解:连接,
,
,
等边三角形,
,
为的中点,
,
.
故答案为:30.
【变式2-3】(2024·上海青浦·模拟预测)如图1,为半圆的直径,点为圆心,为半圆的切线,过半圆上的点作交于点,连接.
(1)连接,若,求证:是半圆的切线;
(2)如图2,当线段与半圆交于点时,连接,,判断和的数量关系,并证明你的结论.
【答案】(1)见解析
(2)
【分析】本题考查了切线的判定和性质,圆周角定理,平行四边形的判定和性质,正确的作出辅助线是解题的关键.
(1)连接,根据切线的性质得到,推出四边形是平行四边形,得到,等量代换得到,推出四边形是平行四边形,根据平行四边形的性质得到,于是得到结论;
(2)如图2,连接,根据圆周角定理得到,求得,证得,等量代换即可得到结论.
【详解】(1)证明:连接,
为半圆的切线,为半圆的直径,
,
∵,,
四边形是平行四边形,
,
,
,
四边形是平行四边形,
∴,
∵,
,
∵,
,
是半圆的切线;
(2)解:,
理由:如图2,连接,
为半圆的直径,
,
,
,
,
,
,
,
.
【题型3 作垂直证半径证明是切线】
【例3】(2024·江苏扬州·中考真题)如图,四边形中,,,,连接,以点B为圆心,长为半径作,交于点E.
(1)试判断与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
【答案】(1)相切,理由见解析;(2)
【分析】(1)过点B作BF⊥CD,证明△ABD≌△FBD,得到BF=BA,即可证明CD与圆B相切;
(2)先证明△BCD是等边三角形,根据三线合一得到∠ABD=30°,求出AD,再利用S△ABD-S扇形ABE求出阴影部分面积.
【详解】解:(1)过点B作BF⊥CD,
∵AD∥BC,
∴∠ADB=∠CBD,
∵CB=CD,
∴∠CBD=∠CDB,
∴∠ADB=∠CDB,又BD=BD,∠BAD=∠BFD=90°,
∴△ABD≌△FBD(AAS),
∴BF=BA,则点F在圆B上,
∴CD与圆B相切;
(2)∵∠BCD=60°,CB=CD,
∴△BCD是等边三角形,
∴∠CBD=60°
∵BF⊥CD,
∴∠ABD=∠DBF=∠CBF=30°,
∴∠ABF=60°,
∵AB=BF=,
∴AD=DF==2,
∴阴影部分的面积=S△ABD-S扇形ABE
=
=.
【点睛】本题考查了切线的判定,全等三角形的判定和性质,等边三角形的判定和性质,扇形面积,三角函数的定义,题目的综合性较强,难度不小,解题的关键是正确做出辅助线.
【变式3-1】(23-24九年级·广西防城港·期末)如图,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与CD相切于点M,
(1)求证:BC与⊙O相切;
(2)若正方形的边长为1,求⊙O的半径.
【答案】(1)证明见解析;(2)
【分析】(1)过作于 由正方形ABCD,可得 证明 再证明 从而可得结论;
(2)正方形ABCD,可得 求解 再证明 求解 利用 列方程,解方程可得答案.
【详解】解:(1)过作于
正方形ABCD,
是的切线,
为的半径,
BC与⊙O相切;
(2) 正方形ABCD,
设的半径为
【点睛】本题考查的是正方形的性质,圆的切线的判定,勾股定理的应用,等腰直角三角形的判定与性质,角平分线的性质,二次根式的运算,掌握以上知识是解题的关键.
【变式3-2】(23-24九年级·山西·期末)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
【答案】(1)证明见解析;(2)8
【分析】(1)过点D作DF⊥AC于F,根据切线的性质可得∠B=90°,即AB⊥BC,然后根据角平分线的性质可得DE=DF,从而证得结论;
(2)根据已知DE=DC和(1)的结论可知DF⊥AC,AB⊥BC以及半径DB=DF,得证Rt△BDE≌Rt△DCF(HL),进而得证EB=FC,再由AB=AF,可知AC=AF+FC=AB+EB=8.
【详解】解:(1)过点D作DF⊥AC于F;
∵AB为⊙D的切线,
∴∠B=90°,
∴AB⊥BC
∵AD平分∠BAC,DF⊥AC,
∴BD=DF,
∴AC与圆D相切;
(2)在△BDE和△DCF中;
∵BD=DF,DE=DC,
∴Rt△BDE≌Rt△DCF(HL),
∴EB=FC.
∵AB=AF,
∴AB+EB=AF+FC,
即AB+EB=AC,
∴AC=5+3=8.
【点睛】本题考查切线的性质与判定,直角三角形全等的判定与性质.
【变式3-3】(23-24九年级·辽宁大连·期末)如图1,为等腰三角形,是底边的中点,腰与相切于点,底交于点,.
(1)求证:是的切线;
(2)如图2,连接,交于点,点是弧的中点,若,,求的半径.
【答案】(1)证明见解析;(2)的半径为2.5.
【分析】(1)连接,,过作于点,根据三线合一可得,然后根据角平分线的性质可得,然后根据切线的判定定理即可证出结论;
(2)连接,过作于点,根据平行线的判定证出,证出,根据角平分线的性质可得,然后利用HL证出,从而得出,设的半径为,根据勾股定理列出方程即可求出结论.
【详解】(1)证明:如图,连接,,过作于点.
∵,是底边的中点,
∴,
∵是的切线,
∴,
∴.
∴是的切线;
(2)解:如图2,连接,过作于点.
∵点是的中点,
∴,
∴
∴,
∴
在和中,
∴
∴
设的半径为
由勾股定理得:DK2+OK2=OD2
即,
解得:.
∴的半径为.
【点睛】此题考查的是等腰三角形的性质、角平分线的性质、切线的判定及性质、全等三角形的判定及性质和勾股定理,掌握等腰三角形的性质、角平分线的性质、切线的判定及性质、全等三角形的判定及性质和勾股定理是解决此题的关键.
【题型4 由切线的性质求线段长度】
【例4】(23-24九年级·重庆忠县·期中)如图,是的内接三角形,.点是延长线上一点,且与相切于点,若的半径为1,则长为( )
A. B. C. D.3
【答案】A
【分析】本题主要考查圆与三角形的综合,掌握圆周角定理,切线的性质,互补的性质,勾股定理是解题的关键.
如图所示,连接,根据圆周角定理可得,根据补角的性质可得,结合题意,与相切于点,可得,,运用勾股定理即可求解.
【详解】解:如图所示,连接,
∵,
∴,
∴,
∵与相切于点,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
故选:A.
【变式4-1】(2024九年级·江苏·专题练习)如图,与相切于点A,交于点B,点C在上,且.若,,则的长为 .
【答案】
【分析】本题考查了圆的切线的性质,全等三角形的判定与性质,勾股定理,熟练掌握圆的切线的性质是解题的关键.根据圆的切线的性质可得,然后根据全等三角形的判定与性质,可得,再根据勾股定理及面积法列方程,即可求解答案.
【详解】解:连接,
与相切于点A,
,
,,,
,
,
在中,,,
,
,
,
,
,
.
故答案为:.
【变式4-2】(2024九年级·江苏·专题练习)如图,是⊙O的直径,,与⊙O相切于点A,交⊙O于点D,连接,若,则的长为( )
A.4 B. C.2 D.
【答案】D
【分析】本题考查了直径所对的圆周角是直角、切线的性质定理、直角三角形的两个锐角互余、等边三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
连接,由是⊙O的直径,,得,,由切线的性质得,而,所以,则是等边三角形,所以,由勾股定理得,于是得到问题的答案.
【详解】解:连接,
∵是⊙O的直径,,
∴,,
∵与⊙O相切于点A,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴.
故选:D.
【变式4-3】(2024·海南海口·模拟预测)如图,与相切于点,与弦相交于点,,若,,则的长为 .
【答案】
【分析】本题考查了切线的性质,等腰三角形的判定和性质,余角性质,对顶角的性质,勾股定义,连接,由切线的性质可得,由得,又由得到,即可根据余角性质得到,进而得到,即得到,设,则,,由勾股定理可得,据此即可求解,正确作出辅助线是解题的关键.
【详解】解:连接,如图,
∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
设,则,,
∵,
∴,
解得,
即的长为,
故答案为:.
【题型5 由切线的性质求角度】
【例5】(2024·海南海口·模拟预测)如图,在中,,圆O与交于点D,与相切于点C,,则 .
【答案】/64度
【分析】本题考查圆的切线的性质,圆周角定理、平行线的判定和性质,解题的关键是熟练掌握圆和平行线的相关知识.
根据同弧对应的圆心角是圆周角的2倍计算出,再根据,内错角得到答案.
【详解】解:如图所示,连接,
∵,
∴.
∵是圆的切线
∴,
∵,
∴,
∴,
∴
故答案为:.
【变式5-1】(23-24九年级·重庆九龙坡·开学考试)如图,是的直径,,垂足为E,直线与相切于点C,交于点D,直线交的延长线于点P,连接,若,则的度数是( )
A. B. C. D.
【答案】A
【分析】连接,由切线的性质,可以证明,由平行线的性质、等腰三角形的性质,得到,由,求出的度数,即可得除答案.
【详解】解:连接,
∵与相切于点C,
∴半径,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
故选:A.
【点睛】本题考查了切线的性质、等腰三角形的性质以及平行线的性质,关键是由条件证明.
【变式5-2】(2024九年级·江苏·专题练习)如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
【答案】A
【分析】本题考查正多边形和圆,切线的性质,掌握正六边形的性质,切线的性质以及多边形内角和的计算方法是正确解答的关键.根据正六边形的性质可求出各个内角的度数,由切线的性质以及五边形内角和的计算方法即可求出答案.
【详解】解:∵正六边形的边,与相切于点C,F,
∴,
∵六边形是正六边形,
∴,
在五边形中,
,
故选:A.
【变式5-3】(2024九年级·全国·专题练习)如图分别切于A、B、E,,则( )
A. B. C. D.
【答案】B
【分析】本题考查了切线的性质,三角形全等的判定与性质,四边形的内角和,根据切线的性质证明,,得到,,进而得到,再根据四边形内角和即可求解.
【详解】解:如图,连接,
∵分别切于A、B、E,
,
在与中,
,
,
∴,
同理,
,
∴,
∵,
∴,
∴.
故选:B.
【题型6 利用切线的性质进行证明】
【例6】(2024·山西大同·三模)如图,以的一边为直径作,点恰好落在上,射线与相切于点.
(1)尺规作图:过点作于点,延长交于点,连接;(保留作图痕迹,标明相应字母,不写作法)
(2)在(1)的条件下证明:.
【答案】(1)见解析
(2)见解析
【分析】(1)根据要求作出图形即可;
(2)利用切线的性质结合求得,得到,以及等腰三角形的性质可证,利用圆周角定理得到,据此即可求解.
【详解】(1)解:所作图形如图所示.
(2)解:如图,连接,
∵是的切线,
∴,即,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了作图—作垂线,切线的性质,圆周角定理,平行线的判定和性质,等边对等角等知识,正确引出辅助线解决问题是解题的关键.
【变式6-1】(23-24九年级·福建莆田·期中)如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,根据切线性质,等角对等边,证明.
(2)连接,根据圆的性质,切线的性质,勾股定理解答即可.
本题考查了切线的性质,圆的性质,勾股定理,熟练掌握切线的性质,勾股定理是解题的关键.
【详解】(1)证明:连接,
∵是切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
∴.
(2)解:连接.
∵,
∴,
∵是的直径,,
∴是的切线,
∴,
∴,
∵,
∴,
在中,,
∴,
设,在中,,
在中,,
∴,
解得,
∴.
【变式6-2】(23-24九年级·安徽蚌埠·期末)如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
【答案】(1)
(2)见详解
【分析】(1)根据等腰三角形的性质得到,求得,根据垂径定理得到,于是得到结论;
(2)连接,,根据切线的性质得到,根据平行线的性质得到,根据等腰三角形的性质得到,求得,根据等腰三角形的性质得到,等量代换得到结论.
本题考查了切线的性质,等腰三角形的判定和性质,平行线的判定和性质,圆周角定理,正确地作出辅助线是解题的关键.
【详解】(1)解:,
,
,
是的直径,,
,
,
故的度数为;
(2)证明:连接,,
是的切线,
,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
,
.
【变式6-3】(2024·广东梅州·模拟预测)如图,P为外一点,为的切线,切点分别为A、B,直线交于点D、E,交于点C.
(1)求证∶.
(2)若,连接,求证:四边形是菱形.
【答案】(1)见解析
(2)见解析
【分析】(1)连接,由,证明,,进而得证;
(2)连接,连接,证明,得到,由为的切线得到,,证明,得到,则,得到,又由,即可证明四边形是菱形.
【详解】(1)证明:如图,连接,
∵是直径,
∴
即
∵为的切线,
∴,
即.
∴,
∵
∴,
∴.
(2)连接,连接,如图,
∵,
∴,
∵为的切线,
∴,
∴,
∴
∵为的切线,
∴,,
∵
∴,
∴
∴
∴,
∵,
∴四边形是菱形.
【点睛】此题考查了切线的性质、切线长定理、圆周角定理、全等三角形的判定和性质、菱形的判定等知识,添加适当的辅助线是证明的关键.
【题型7 作圆的切线】
【例7】(2024·江苏镇江·一模)如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上.
(1)的周长为______.
(2)请在如图所示的网格中,用无刻度的直尺在上确定一点,使以点为圆心,以为半径的与相切.(保留作图痕迹)
【答案】(1)12
(2)见解析
【分析】(1)根据勾股定理求出,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质、角平分线的性质、切线的判定定理作图即可.
【详解】(1)解:由勾股定理得:,
则的周长,
故答案为:12;
(2)延长至,使,连接,取的中点,连接交于点,
则点即为所求.
【点睛】本题考查的是勾股定理、切线的判定定理、角平分线的性质、等腰三角形的性质,掌握切线的判定定理是解题的关键.
【变式7-1】(23-24九年级·广东广州·期末)如图,直角梯形中,,,.
(1)尺规作出以为直径的圆(保留作图痕迹,不写作法);
(2)判断与的位置关系,并说明理由.
【答案】(1)见解析
(2)与相切,理由见解析
【分析】(1)根据题意作出线段的垂直平分线,交于点O,然后以O为圆心以为半径画圆即可;
(2)在线段上作,连接,根据题意证明出,然后证明出,进而求解即可.
【详解】(1)如图所示,即为所要求作的以为直径的圆.
(2)在线段上作,连接,,,,
∵,,
∴,
∵,
∴,
∴,,
∵,,
∴,
∴,
∵为圆的直径,
∴点E在上,
∴在和中,
∴,
∴,
∴,
∴与相切.
【点睛】此题考查了垂直平分线的尺规作图,切线的判定,全等三角形的性质和判定等知识,解题的关键是熟练掌握以上知识点.
【变式7-2】(2024·吉林长春·模拟预测)如图,在每个小正方形的边长为1的网格中,的顶点A,B,以为直径的半圆的圆心为O,仅用无刻度的直尺在给定网格中完成画图:
(1)请在图1中作出的边上的高;
(2)请在图2中线段上确定一点F,使得;
(3)请在图3中作出的切线.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】本题考查作图 复杂作图,圆周角定理,切线的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)延长交于点D,连接即可;
(2)利用三角形的三条中线交于一点解决问题即可;
(3)取格点E,连接即可.
【详解】(1)解:如图1中,线段即为所求;
(2)解:如图2中,线段即为所求;
(3)解:如图3中,直线即为所求.
【变式7-3】(2024·山东德州·中考真题)如图,,点、分别在射线、上,,.
(1)用尺规在图中作一段劣弧,使得它在、两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;
(3)求所得的劣弧与线段、围成的封闭图形的面积.
【答案】(1)详见解析;(2)详见解析;(3)
【分析】(1)过、分别作、的垂线,它们相交于,然后以为半径作即可;
(2)写出已知、求证,然后进行证明;连接,先证明,然后根据切线的判定方法判断、为的切线;
(3)先证明为等边三角形得到,,再计算出,然后根据扇形的面积公式,利用劣弧与线段、围成的封闭图形的面积进行计算.
【详解】(1)如图,
(2)已知:如图,,点、分别在射线、上,,,过、分别作、的垂线,它们相交于,以为半径作,,
求证:、为的切线;
证明:∵,,
,
,
连接,
∵,,
,
∵,
,
、为的切线;
(3)∵,
为等边三角形,
,,
∵平分,
,
,
劣弧与线段、围成的封闭图形的面积 .
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了圆周角定理和扇形面积公式.
【题型8 利用切线的判定与性质判断结论正误】
【例8】(2024九年级·安徽·专题练习)如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【答案】A
【分析】由DB=DC,OA=OB,推出OD是△ABC的中位线,OD∥AC,由DF⊥AC,得出DF⊥OD,即DF是☉O的切线,继而证得△ABC是等腰三角形,根据等腰三角形的性质可得∠B=∠C,进而推出△DEC是等腰三角形,进而根据等腰三角形的性质可得CF=EF,由假设推出进而即可求解.
【详解】如图,连接OD,DE,AD,
∵DB=DC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是☉O的切线,故①正确;
∵∠CED+∠AED=180°,∠B+∠AED=180°,
∴∠CED=∠B,
∵AB是☉O的直径,
∴∠ADB=90°,即AD⊥BC,
∵BD=CD,
∴AB=AC,
∴∠B=∠C,
∴∠CED=∠C,
∴DC=DE,
又∵DF⊥AC,
∴CF=EF,故②正确;
当∠EAD=∠EDA时, ,此时△ABC为等边三角形,当△ABC不是等边三角形时,∠EAD≠∠EDA,则
∴不一定正确,
综上,正确结论的序号是①②,
故选A.
【点睛】本题考查切线的判定及其性质,等腰三角形的判定及其性质,圆周角定理、线段垂直平分线的性质,圆内接四边形的性质等知识,综合性较强,解题的关键是熟练掌握并灵活运用所学知识.
【变式8-1】(23-24九年级·安徽合肥·期末)为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
【答案】C
【分析】本题考查了等腰三角形的性质,三角形的外角性质,切线的判定和性质.利用等腰三角形的性质结合三角形的外角性质即可判断选项A、B、D正确;假设成立,证明是等边三角形,推出是的切线,与题设相矛盾,可判断选项C不正确.
【详解】解:连接,
∵平分,
∴设,
若,
∴,
则,选项A正确,不符合题意;
若,又∵,
∴,
∴,选项B正确,不符合题意;
若切于点,
∴,即,
∴,
∵,
∴,
∴,选项D正确,不符合题意;
连接,假设成立,
∵为的直径,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴点在以为直径的圆上,即,
∴切于点,
而题设并没有是的切线这一条件,
∴假设不成立,选项C不正确,符合题意.
故选:C.
【变式8-2】(2014·江苏无锡·中考真题)如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
【答案】A
【详解】解:连接OD,
∵CD是⊙O的切线,
∴CD⊥OD,
∴∠ODC=90°,
又∵∠A=30°,
∴∠ABD=60°,
又∵OB=OD,
∴△OBD是等边三角形.
∴∠DOB=∠ABD=60°,AB=2OB=2OD=2BD.
∴∠C=∠BDC=30°.
∴BD=BC,②成立.
∴AB=2BC,③成立.
∴∠A=∠C.
∴DA=DC,①成立.
综上所述,①②③均成立.
故选:A.
【点睛】本题考查切线的性质;直角三角形两锐角的关系;等边三角形的判定和性质;等腰三角形的判定.
【变式8-3】(23-24九年级·河北保定·期中)在黑板上有如下内容:“如图,是半圆所在圆的直径,,点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目,下列判断正确的是( )
嘉嘉:若给出,则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且,则可求出的面积.
A.只有嘉嘉的正确 B.只有淇淇的正确
C.嘉嘉和淇淇的都不正确 D.嘉嘉和淇淇的都正确
【答案】D
【分析】根据切线的求证方法,如图所示(见详解),连接,证明即可求解;根据切线的性质,,可求出等腰三角形,等边三角形,根据含特殊角的直角三角形的直线可求出各边的长度,由此即可求解.
【详解】解:∵是半圆所在圆的直径,
∴,
如图所示,连接,
∵是半径,
∴,
∵,
∴,
嘉嘉给出的条件是:,
∴,即,且点在圆上,
∴直线是半圆的切线,故嘉嘉给出的条件正确;
淇淇给出的条件:直线是的切线,且,如图所示,
∴,且是等腰三角形,
∴,
∴,
∵,,
∴,且,
∴是等边三角形,
∴,
∵,
∴,
∴,
如图所示,过点作于,
在是等边三角形,,
∴,故淇淇给出的条件正确,
故选:.
【点睛】本题主要考查圆与特殊角的直角三角形的综合,掌握圆切线的求证方法,含特殊角的直角三角形的性质,等边三角形的性质是解题的关键.
【题型9 利用切线的判定与性质进行求值或证明】
【例9】(23-24九年级·黑龙江哈尔滨·阶段练习)如图,中,,点在边上,过点且分别与边、相交于、两点,,点为垂足.
(1)求证:直线是的切线;
(2)当是等边三角形,且直线与相切时,直接写出长度为线段长度2倍的所有线段.
【答案】(1)见解析
(2)长度为线段长度2倍的所有线段有:,,,.
【分析】(1)利用等腰三角形的性质,同圆的半径相等,平行线的判定与性质和圆的切线的判定定理解答即可;
(2)连接,利用圆周角定理和含角的直角三角形的性质,得到;再利用圆的切线的性质定理,等边三角形的性质和直角三角形的性质,全等三角形的判定与性质解答即可得出结论.
【详解】(1)证明:连接,如图,
,
.
,
,
,
.
,
,
为的半径,
直线是的切线;
(2)解:连接,如图,
为的直径,
,
是等边三角形,
,
,
.
,
,
.
直线与相切,
,
,
,
为等边三角形,
.
在和中,
,
,
.
同理:,
.
.
由题意:,
,
,
长度为线段长度2倍的所有线段有:,,,.
【点睛】本题主要考查了等腰三角形的性质,等边三角形的性质,圆的有关性质,圆的切线的判定,圆周角定理,全等三角形的判定与性质,含角的直角三角形的性质,连接经过切点的半径是解决此类问题常添加的辅助线.
【变式9-1】(2024·辽宁沈阳·二模)如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点,且,连接.
(1)求证:是的切线;
(2)若,,求的半径的长.
【答案】(1)证明见解析
(2)
【分析】本题主要考查了切线的性质与判定, 等弧所对的圆心角相等,全等三角形的性质与判定,勾股定理等等:
(1)如图所示,连接,由切线的性质得到,再由得到,证明,得到,据此可证明结论;
(2)设的半径为r,则,在中利用勾股定理建立方程求解即可.
【详解】(1)证明:如图所示,连接,
∵与相切于点B,
∴ ,
∵,
∴,
又∵,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解:设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为.
【变式9-2】(2024·陕西西安·模拟预测)如图,在中,以边上一点O为圆心,为半径作,与相切于点A.作交的延长线于点D,且.
(1)求证:是的切线;
(2)若,,求⊙O的半径.
【答案】(1)见解析
(2)
【分析】(1)过O点作于点E,推导出,然后根据角平分线的性质即可得到,证明结论;
(2)先利用勾股定理求出长,然后利用全等三角形得到,然后再在中利用勾股定理解题即可.
【详解】(1)证明:过O点作于点E,
∵与相切于点A,
∴
又∵,
∴,
∵,
∴,
又∵,,
∴,
∴是的切线;
(2)解:∵,,
∴,
在和中,
,
∴,
∴,
∴,
在中,,即,
解得:.
【点睛】本题考查切线的判定与性质,角平分线的性质,勾股定理,全等三角形的判定与性质,解题的关键是掌握切线的判定和性质.
【变式9-3】(23-24九年级·广东·单元测试)如图1,为直径,与相切于点B,D为上一点,连接,若.
(1)求证:为的切线;
(2)如图2,过点A作交延长线于点E,连接交于点F,若,求的长.
【答案】(1)详见解析
(2)
【分析】(1)连接,由切线的性质得出,证明,由全等三角形的性质得出,则可得出结论;
(2)设,根据切线长定理可得,过点E作于M,可得,由勾股定理求出,求出的长,则可得出答案.
【详解】(1)证明:连接,
∵与相切,
∴,即,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
又为半径,
∴为的切线;
(2)解:如图,连接,
设,
∵,
∴,
∵,
∴为的切线,
∵为的切线,
∴,,
∴,
∵,
∴垂直平分,
∴,
过点E作于M,则,
∴四边形是矩形,
∴,
∴,
在中,,
∴,解得,
∴,
∴,
∵,
∴.
【点睛】此题主要考查了切线的判定和性质、全等三角形的判定和性质、勾股定理、切线长定理等知识的综合应用,是一道综合性较强的题目.
【题型10 切线的应用】
【例10】(2024·福建宁德·二模)综合与实践:
任务一:确定弦的长度.如图2,求所对弦的长度.
任务二:设计甲组扇面.如图3,已知甲组的圆形卡纸直径为.请运用所给工具在中设计与图2相同的扇面,并标出相应数据.
任务三:确定卡纸大小.如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2,扇面形状为扇环,且,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【答案】任务一:, 任务二:见解析;任务三:矩形的边长为、.
【分析】本题考查了垂径定理,含角的直角三角形,解题的关键是:熟练掌握相关性质定理.
任务一:由弧所对的圆心角为,可得,求得,应用勾股定理求出,即可求解,
任务二:以直径为底边,构造底角为30度的等腰三角形,则得到的三角形和任务一三角形全等,再按要求取点,再以为圆心,分别以、为半径画弧,得到的扇面图形与图2相同;
任务三:在上取一点使,以为圆心,为半径的圆与相切,此时点与点重合,在圆上取一点A,使,即可得到扇面.过点作,则矩形为最小规格矩形,
【详解】任务一:解:过点O作,交于点,
,,
,
,
,,
,
任务二:如图,是以直径为底边,底角为度,由任务一可知,,取,以O为圆心,分别以、为半径画弧,即可得到扇面.
任务三:如图所示:当与矩形两边相切时,过点作,则矩形为最小规格矩形,
∵,,,
∴,,,
∵当与矩形两边相切,
∴最小规格矩形的边长为、,
【变式10-1】(23-24九年级·浙江杭州·)图1是一种推磨工具模型,图2是它的示意图,已知,,点A在中轴线上运动,点B在以O为圆心,长为半径的圆上运动,且,如图3,当点B按逆时针方向运动到时,与相切,则 .
【答案】
【分析】由题意得到A′A=OA-OA′=AB+OB-OA′,即可求解.
【详解】解:由题意可得:
A′A=OA-OA′=AB+OB-OA′=12+4-==,
故答案为:.
【点睛】本题考查的是切线的性质,勾股定理,解题的关键是确定转动后图形重要点的位置关系.
【变式10-2】(2024·河北邯郸·模拟预测)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具.图1,图2是某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,是粒子真空室,C、D是两个加速电极,高速飞行的粒子J在A点注入,在粒子真空室内做环形运动,每次经过 时被加速,达到一定的速度在B点引出,粒子注入和引出路径都与相切.已知:,粒子注入路径与夹角,所对的圆心角是.
(1)求的度数;
(2)通过计算,比较与的长度哪个更长;
(3)直接写出粒子J在环形运动过程中,粒子J到的最远距离.(相关数据: )
【答案】(1)
(2)的长度更长,见解析
(3)粒子J到的最远距离是
【分析】(1)如图,延长交于G,根据切线长定理和等腰三角形的性质即可得到结论;
(2)根据弧长公式求出的长,再进行比较即可;
(3)如图,当粒子J运动到P点时,离的距离最远,根据切线的性质得到,再根据垂径定理和三角函数得出的长,进而解答即可
【详解】(1)解:如图,延长交于G,
由题意得,是的切线,
∴,
∴;
(2)解:的长度更长,
∵所对的圆心角为,,
∴的长度约为,
∵,
∴的长度更长;
(3)解:如图,过点O作于点E,延长交于点P,连接,
∵是的切线,
∴,
∵,
∴,
∵是的弦,是弦心距,,
∴,,
∴,
∴,
∴,
如图,当粒子J运动到P点时,离的距离最远,
∴,
即粒子J到的最远距离是.
【点睛】本题是圆的综合题,涉及圆周角定理,圆切线的性质,垂径定理,解直角三角形,弧长公式,正确作出辅助线是解题关键.
【变式10-3】(2013·浙江温州·中考真题)一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线切割,如图1所示.图2中的矩形是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则的长分别是 .
【答案】18cm, 31cm.
【分析】如图,延长交线段于点,延长交于点G,交于点,设圆孔半径为r.根据勾股定理,得.从而得.根据题意知,.则根据图中相关线段间的和差关系求得CN=QH-QN2=44-26=18, AM=BC-PD-KM1=130-50-49=31 ( cm).
【详解】解:作辅助线如图所示,设圆孔半径为r,
根据勾股定理,得.
∴,
.
按题意要求,切割后,以圆O为中心,到两对边的距离相等,
即:.
∵,
∴ QN2+r=42,即QN2=42-16=26.
∴CN=QH-QN2=44-26=18.
又∵,即 ,
∴ KM1=49.
∴AM=BC-PD-KM1=130-50-49=31.
∴CN=18cm,AM=31cm.
故答案为:18cm,31cm
【点睛】本题考查了矩形、直角三角形及圆等相关知识,将实际问题转化为数学问题经验,利用图形变换思想是解题的关键,体现了数学思想方法在现实问题中的应用价值.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 添加条件使直线为切线】 1
【题型2 连半径证垂直证明是切线】 2
【题型3 作垂直证半径证明是切线】 4
【题型4 由切线的性质求线段长度】 5
【题型5 由切线的性质求角度】 6
【题型6 利用切线的性质进行证明】 7
【题型7 作圆的切线】 9
【题型8 利用切线的判定与性质判断结论正误】 10
【题型9 利用切线的判定与性质进行求值或证明】 11
【题型10 切线的应用】 13
知识点:切线的判定与性质
(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线
②和圆只有一个公共点的直线是圆的切线(定义法)
③如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
(2)切线判定常用的证明方法:
①知道直线和圆有公共点时,连半径,证垂直;
②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.
(3)切线的性质:圆的切线垂直于经过切点的半径.
【题型1 添加条件使直线为切线】
【例1】(23-24九年级·河北衡水·阶段练习)如图,是的直径,是上一点,是外一点,过点作,垂足为,连接.若使切于点,添加的下列条件中,不正确的是( )
A. B. C. D.
【变式1-1】(23-24九年级·全国·课后作业)如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
【变式1-2】(23-24九年级·全国·期末)如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
【变式1-3】(23-24九年级·北京·期末)在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
【题型2 连半径证垂直证明是切线】
【例2】(2024九年级·江苏·专题练习)已知是的直径,点是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为,的半径为,求的长.
【变式2-1】(2024·江苏镇江·中考真题)如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
【变式2-2】(2024·山东青岛·一模)如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
【变式2-3】(2024·上海青浦·模拟预测)如图1,为半圆的直径,点为圆心,为半圆的切线,过半圆上的点作交于点,连接.
(1)连接,若,求证:是半圆的切线;
(2)如图2,当线段与半圆交于点时,连接,,判断和的数量关系,并证明你的结论.
【题型3 作垂直证半径证明是切线】
【例3】(2024·江苏扬州·中考真题)如图,四边形中,,,,连接,以点B为圆心,长为半径作,交于点E.
(1)试判断与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
【变式3-1】(23-24九年级·广西防城港·期末)如图,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与CD相切于点M,
(1)求证:BC与⊙O相切;
(2)若正方形的边长为1,求⊙O的半径.
【变式3-2】(23-24九年级·山西·期末)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
【变式3-3】(23-24九年级·辽宁大连·期末)如图1,为等腰三角形,是底边的中点,腰与相切于点,底交于点,.
(1)求证:是的切线;
(2)如图2,连接,交于点,点是弧的中点,若,,求的半径.
【题型4 由切线的性质求线段长度】
【例4】(23-24九年级·重庆忠县·期中)如图,是的内接三角形,.点是延长线上一点,且与相切于点,若的半径为1,则长为( )
A. B. C. D.3
【变式4-1】(2024九年级·江苏·专题练习)如图,与相切于点A,交于点B,点C在上,且.若,,则的长为 .
【变式4-2】(2024九年级·江苏·专题练习)如图,是⊙O的直径,,与⊙O相切于点A,交⊙O于点D,连接,若,则的长为( )
A.4 B. C.2 D.
【变式4-3】(2024·海南海口·模拟预测)如图,与相切于点,与弦相交于点,,若,,则的长为 .
【题型5 由切线的性质求角度】
【例5】(2024·海南海口·模拟预测)如图,在中,,圆O与交于点D,与相切于点C,,则 .
【变式5-1】(23-24九年级·重庆九龙坡·开学考试)如图,是的直径,,垂足为E,直线与相切于点C,交于点D,直线交的延长线于点P,连接,若,则的度数是( )
A. B. C. D.
【变式5-2】(2024九年级·江苏·专题练习)如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
【变式5-3】(2024九年级·全国·专题练习)如图分别切于A、B、E,,则( )
A. B. C. D.
【题型6 利用切线的性质进行证明】
【例6】(2024·山西大同·三模)如图,以的一边为直径作,点恰好落在上,射线与相切于点.
(1)尺规作图:过点作于点,延长交于点,连接;(保留作图痕迹,标明相应字母,不写作法)
(2)在(1)的条件下证明:.
【变式6-1】(23-24九年级·福建莆田·期中)如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
【变式6-2】(23-24九年级·安徽蚌埠·期末)如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
【变式6-3】(2024·广东梅州·模拟预测)如图,P为外一点,为的切线,切点分别为A、B,直线交于点D、E,交于点C.
(1)求证∶.
(2)若,连接,求证:四边形是菱形.
【题型7 作圆的切线】
【例7】(2024·江苏镇江·一模)如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上.
(1)的周长为______.
(2)请在如图所示的网格中,用无刻度的直尺在上确定一点,使以点为圆心,以为半径的与相切.(保留作图痕迹)
【变式7-1】(23-24九年级·广东广州·期末)如图,直角梯形中,,,.
(1)尺规作出以为直径的圆(保留作图痕迹,不写作法);
(2)判断与的位置关系,并说明理由.
【变式7-2】(2024·吉林长春·模拟预测)如图,在每个小正方形的边长为1的网格中,的顶点A,B,以为直径的半圆的圆心为O,仅用无刻度的直尺在给定网格中完成画图:
(1)请在图1中作出的边上的高;
(2)请在图2中线段上确定一点F,使得;
(3)请在图3中作出的切线.
【变式7-3】(2024·山东德州·中考真题)如图,,点、分别在射线、上,,.
(1)用尺规在图中作一段劣弧,使得它在、两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;
(3)求所得的劣弧与线段、围成的封闭图形的面积.
【题型8 利用切线的判定与性质判断结论正误】
【例8】(2024九年级·安徽·专题练习)如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【变式8-1】(23-24九年级·安徽合肥·期末)为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
【变式8-2】(2014·江苏无锡·中考真题)如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
【变式8-3】(23-24九年级·河北保定·期中)在黑板上有如下内容:“如图,是半圆所在圆的直径,,点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目,下列判断正确的是( )
嘉嘉:若给出,则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且,则可求出的面积.
A.只有嘉嘉的正确 B.只有淇淇的正确
C.嘉嘉和淇淇的都不正确 D.嘉嘉和淇淇的都正确
【题型9 利用切线的判定与性质进行求值或证明】
【例9】(23-24九年级·黑龙江哈尔滨·阶段练习)如图,中,,点在边上,过点且分别与边、相交于、两点,,点为垂足.
(1)求证:直线是的切线;
(2)当是等边三角形,且直线与相切时,直接写出长度为线段长度2倍的所有线段.
【变式9-1】(2024·辽宁沈阳·二模)如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点,且,连接.
(1)求证:是的切线;
(2)若,,求的半径的长.
【变式9-2】(2024·陕西西安·模拟预测)如图,在中,以边上一点O为圆心,为半径作,与相切于点A.作交的延长线于点D,且.
(1)求证:是的切线;
(2)若,,求⊙O的半径.
【变式9-3】(23-24九年级·广东·单元测试)如图1,为直径,与相切于点B,D为上一点,连接,若.
(1)求证:为的切线;
(2)如图2,过点A作交延长线于点E,连接交于点F,若,求的长.
【题型10 切线的应用】
【例10】(2024·福建宁德·二模)综合与实践:
任务一:确定弦的长度.如图2,求所对弦的长度.
任务二:设计甲组扇面.如图3,已知甲组的圆形卡纸直径为.请运用所给工具在中设计与图2相同的扇面,并标出相应数据.
任务三:确定卡纸大小.如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2,扇面形状为扇环,且,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【变式10-1】(23-24九年级·浙江杭州·)图1是一种推磨工具模型,图2是它的示意图,已知,,点A在中轴线上运动,点B在以O为圆心,长为半径的圆上运动,且,如图3,当点B按逆时针方向运动到时,与相切,则 .
【变式10-2】(2024·河北邯郸·模拟预测)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具.图1,图2是某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,是粒子真空室,C、D是两个加速电极,高速飞行的粒子J在A点注入,在粒子真空室内做环形运动,每次经过 时被加速,达到一定的速度在B点引出,粒子注入和引出路径都与相切.已知:,粒子注入路径与夹角,所对的圆心角是.
(1)求的度数;
(2)通过计算,比较与的长度哪个更长;
(3)直接写出粒子J在环形运动过程中,粒子J到的最远距离.(相关数据: )
【变式10-3】(2013·浙江温州·中考真题)一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线切割,如图1所示.图2中的矩形是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则的长分别是 .
21世纪教育网(www.21cnjy.com)
专题24.6 切线的判定与性质【十大题型】
【人教版】
【题型1 添加条件使直线为切线】 2
【题型2 连半径证垂直证明是切线】 5
【题型3 作垂直证半径证明是切线】 10
【题型4 由切线的性质求线段长度】 16
【题型5 由切线的性质求角度】 21
【题型6 利用切线的性质进行证明】 25
【题型7 作圆的切线】 31
【题型8 利用切线的判定与性质判断结论正误】 37
【题型9 利用切线的判定与性质进行求值或证明】 43
【题型10 切线的应用】 51
知识点:切线的判定与性质
(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线
②和圆只有一个公共点的直线是圆的切线(定义法)
③如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
(2)切线判定常用的证明方法:
①知道直线和圆有公共点时,连半径,证垂直;
②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.
(3)切线的性质:圆的切线垂直于经过切点的半径.
【题型1 添加条件使直线为切线】
【例1】(23-24九年级·河北衡水·阶段练习)如图,是的直径,是上一点,是外一点,过点作,垂足为,连接.若使切于点,添加的下列条件中,不正确的是( )
A. B. C. D.
【答案】D
【分析】本题考查切线的证明,涉及圆的切线的判定、平行线的判定与性质、圆的性质等知识,根据选项,逐项判定即可得到答案,熟记圆的切线的判定是解决问题的关键.
【详解】解:A、 ,
,
当时,则,即,根据切线的判定,切于点,该选项正确,不符合题意;
B、 ,
,则,
,
,
当时,则,即,根据切线的判定,切于点,该选项正确,不符合题意;
C、当时,,
,
,
,即,根据切线的判定,切于点,该选项正确,不符合题意;
D、当时,由得到,则是等腰三角形,无法确定,不能得到切于点,该选项不正确,符合题意;
故选:D.
【变式1-1】(23-24九年级·全国·课后作业)如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
【答案】4
【分析】过M作MN⊥OA于点N,此时以MN为半径的圆与OA相切,根据30°角所对直角边为斜边的一半可得OM的长.
【详解】解:如图,过M作MN⊥OA于点N,
∵MN=2cm,,
∴OM=4cm,
则当OM=4cm时,与OA相切.
故答案为4.
【点睛】本题主要考查切线判定,直角三角形中30°角所对直角边为斜边的一半,解此题的关键在于熟练掌握其知识点.
【变式1-2】(23-24九年级·全国·期末)如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
【答案】60
【分析】由已知可求得∠OAB的度数,因为OA⊥AC,AC才能成为⊙O的切线,从而可求得∠CAB的度数.
【详解】解:∵△AOB中,OA=OB,∠AOB=120°,
∴,
∵当OA⊥AC即∠OAC=90°时,AC才能成为⊙O的切线,
∴当∠CAB的度数等于60°,即OA⊥AC时,AC才能成为⊙O的切线.
故答案为:60.
【点睛】本题考查了切线的判定,三角形内角和定理,等腰三角形的性质,掌握切线的判定定理是解答此题的关键.
【变式1-3】(23-24九年级·北京·期末)在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
【答案】∠ABT=∠ATB=45°(答案不唯一)
【分析】根据切线的判定条件,只需要得到∠BAT=90°即可求解,因此只需要添加条件:∠ABT=∠ATB=45°即可.
【详解】解:添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,
∴∠BAT=90°,
又∵AB是圆O的直径,
∴AT是圆O的切线,
故答案为:∠ABT=∠ATB=45°(答案不唯一).
【点睛】本题主要考查了圆切线的判定,三角形内角和定理,熟知圆切线的判定条件是解题的关键.
【题型2 连半径证垂直证明是切线】
【例2】(2024九年级·江苏·专题练习)已知是的直径,点是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为,的半径为,求的长.
【答案】(1)见解析
(2)
【分析】本题主要考查了切线的判定、同弧所对的圆周角相等、等边对等角、圆周角定理、三角形内角和定理、垂径定理、含度角的直角三角形的性质、勾股定理等知识,灵活运用知识点推理证明是解题的关键.
(1)连接,根据同弧所对的圆周角相等得到,由等边对等角得到,利用圆周角定理得到,利用三角形内角和定理,求得,即可证明直线是的切线;
(2)根据垂径定理得到,根据含度角的直角三角形的性质,得到,根据勾股定理计算,由,得出答案即可.
【详解】(1)证明:如图,连接,
∵,
∴,,
∵,
∴,
∴,
∴,
又∵是的半径,
∴直线是的切线;
(2)解:如图,连接,
∵是的直径,,垂足为,的半径为,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴.
【变式2-1】(2024·江苏镇江·中考真题)如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
【答案】与相切,理由见解析
【分析】连接,由等腰三角形的性质得,再由折叠的性质得,进而证明,则,因此,然后由切线的判定即可得出结论.
【详解】解:与相切.
证明:连接.
∵,
∴.
∵图形沿过点A的直线翻折,点C的对应点落在边上,
∴.
∴.
∴.
∴由,得,即.
∴与相切.
【点睛】本题考查直线与圆的位置关系、等腰三角形的性质、折叠的性质以及平行线的判定与性质等知识,熟练掌握切线的判定和折叠的性质是解题的关键.
【变式2-2】(2024·山东青岛·一模)如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
【答案】(1)是的切线,理由见解析;
(2)30
【分析】本题考查切线的判定,等边三角形的判定及性质,圆周角定理,关键是掌握切线的判定方法,圆周角定理.
(1)由圆周角定理得到,由等腰三角形的性质得到,即可证明问题;
(2)连接,得到是等边三角形,得到,由为的中点,得到,由圆周角定理即可求出的度数.
【详解】(1)解:是的切线,理由如下,
连接,
是圆的直径,
,
,
,
,
,
,
,
半径,
是的切线;
(2)解:连接,
,
,
等边三角形,
,
为的中点,
,
.
故答案为:30.
【变式2-3】(2024·上海青浦·模拟预测)如图1,为半圆的直径,点为圆心,为半圆的切线,过半圆上的点作交于点,连接.
(1)连接,若,求证:是半圆的切线;
(2)如图2,当线段与半圆交于点时,连接,,判断和的数量关系,并证明你的结论.
【答案】(1)见解析
(2)
【分析】本题考查了切线的判定和性质,圆周角定理,平行四边形的判定和性质,正确的作出辅助线是解题的关键.
(1)连接,根据切线的性质得到,推出四边形是平行四边形,得到,等量代换得到,推出四边形是平行四边形,根据平行四边形的性质得到,于是得到结论;
(2)如图2,连接,根据圆周角定理得到,求得,证得,等量代换即可得到结论.
【详解】(1)证明:连接,
为半圆的切线,为半圆的直径,
,
∵,,
四边形是平行四边形,
,
,
,
四边形是平行四边形,
∴,
∵,
,
∵,
,
是半圆的切线;
(2)解:,
理由:如图2,连接,
为半圆的直径,
,
,
,
,
,
,
,
.
【题型3 作垂直证半径证明是切线】
【例3】(2024·江苏扬州·中考真题)如图,四边形中,,,,连接,以点B为圆心,长为半径作,交于点E.
(1)试判断与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
【答案】(1)相切,理由见解析;(2)
【分析】(1)过点B作BF⊥CD,证明△ABD≌△FBD,得到BF=BA,即可证明CD与圆B相切;
(2)先证明△BCD是等边三角形,根据三线合一得到∠ABD=30°,求出AD,再利用S△ABD-S扇形ABE求出阴影部分面积.
【详解】解:(1)过点B作BF⊥CD,
∵AD∥BC,
∴∠ADB=∠CBD,
∵CB=CD,
∴∠CBD=∠CDB,
∴∠ADB=∠CDB,又BD=BD,∠BAD=∠BFD=90°,
∴△ABD≌△FBD(AAS),
∴BF=BA,则点F在圆B上,
∴CD与圆B相切;
(2)∵∠BCD=60°,CB=CD,
∴△BCD是等边三角形,
∴∠CBD=60°
∵BF⊥CD,
∴∠ABD=∠DBF=∠CBF=30°,
∴∠ABF=60°,
∵AB=BF=,
∴AD=DF==2,
∴阴影部分的面积=S△ABD-S扇形ABE
=
=.
【点睛】本题考查了切线的判定,全等三角形的判定和性质,等边三角形的判定和性质,扇形面积,三角函数的定义,题目的综合性较强,难度不小,解题的关键是正确做出辅助线.
【变式3-1】(23-24九年级·广西防城港·期末)如图,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与CD相切于点M,
(1)求证:BC与⊙O相切;
(2)若正方形的边长为1,求⊙O的半径.
【答案】(1)证明见解析;(2)
【分析】(1)过作于 由正方形ABCD,可得 证明 再证明 从而可得结论;
(2)正方形ABCD,可得 求解 再证明 求解 利用 列方程,解方程可得答案.
【详解】解:(1)过作于
正方形ABCD,
是的切线,
为的半径,
BC与⊙O相切;
(2) 正方形ABCD,
设的半径为
【点睛】本题考查的是正方形的性质,圆的切线的判定,勾股定理的应用,等腰直角三角形的判定与性质,角平分线的性质,二次根式的运算,掌握以上知识是解题的关键.
【变式3-2】(23-24九年级·山西·期末)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
【答案】(1)证明见解析;(2)8
【分析】(1)过点D作DF⊥AC于F,根据切线的性质可得∠B=90°,即AB⊥BC,然后根据角平分线的性质可得DE=DF,从而证得结论;
(2)根据已知DE=DC和(1)的结论可知DF⊥AC,AB⊥BC以及半径DB=DF,得证Rt△BDE≌Rt△DCF(HL),进而得证EB=FC,再由AB=AF,可知AC=AF+FC=AB+EB=8.
【详解】解:(1)过点D作DF⊥AC于F;
∵AB为⊙D的切线,
∴∠B=90°,
∴AB⊥BC
∵AD平分∠BAC,DF⊥AC,
∴BD=DF,
∴AC与圆D相切;
(2)在△BDE和△DCF中;
∵BD=DF,DE=DC,
∴Rt△BDE≌Rt△DCF(HL),
∴EB=FC.
∵AB=AF,
∴AB+EB=AF+FC,
即AB+EB=AC,
∴AC=5+3=8.
【点睛】本题考查切线的性质与判定,直角三角形全等的判定与性质.
【变式3-3】(23-24九年级·辽宁大连·期末)如图1,为等腰三角形,是底边的中点,腰与相切于点,底交于点,.
(1)求证:是的切线;
(2)如图2,连接,交于点,点是弧的中点,若,,求的半径.
【答案】(1)证明见解析;(2)的半径为2.5.
【分析】(1)连接,,过作于点,根据三线合一可得,然后根据角平分线的性质可得,然后根据切线的判定定理即可证出结论;
(2)连接,过作于点,根据平行线的判定证出,证出,根据角平分线的性质可得,然后利用HL证出,从而得出,设的半径为,根据勾股定理列出方程即可求出结论.
【详解】(1)证明:如图,连接,,过作于点.
∵,是底边的中点,
∴,
∵是的切线,
∴,
∴.
∴是的切线;
(2)解:如图2,连接,过作于点.
∵点是的中点,
∴,
∴
∴,
∴
在和中,
∴
∴
设的半径为
由勾股定理得:DK2+OK2=OD2
即,
解得:.
∴的半径为.
【点睛】此题考查的是等腰三角形的性质、角平分线的性质、切线的判定及性质、全等三角形的判定及性质和勾股定理,掌握等腰三角形的性质、角平分线的性质、切线的判定及性质、全等三角形的判定及性质和勾股定理是解决此题的关键.
【题型4 由切线的性质求线段长度】
【例4】(23-24九年级·重庆忠县·期中)如图,是的内接三角形,.点是延长线上一点,且与相切于点,若的半径为1,则长为( )
A. B. C. D.3
【答案】A
【分析】本题主要考查圆与三角形的综合,掌握圆周角定理,切线的性质,互补的性质,勾股定理是解题的关键.
如图所示,连接,根据圆周角定理可得,根据补角的性质可得,结合题意,与相切于点,可得,,运用勾股定理即可求解.
【详解】解:如图所示,连接,
∵,
∴,
∴,
∵与相切于点,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
故选:A.
【变式4-1】(2024九年级·江苏·专题练习)如图,与相切于点A,交于点B,点C在上,且.若,,则的长为 .
【答案】
【分析】本题考查了圆的切线的性质,全等三角形的判定与性质,勾股定理,熟练掌握圆的切线的性质是解题的关键.根据圆的切线的性质可得,然后根据全等三角形的判定与性质,可得,再根据勾股定理及面积法列方程,即可求解答案.
【详解】解:连接,
与相切于点A,
,
,,,
,
,
在中,,,
,
,
,
,
,
.
故答案为:.
【变式4-2】(2024九年级·江苏·专题练习)如图,是⊙O的直径,,与⊙O相切于点A,交⊙O于点D,连接,若,则的长为( )
A.4 B. C.2 D.
【答案】D
【分析】本题考查了直径所对的圆周角是直角、切线的性质定理、直角三角形的两个锐角互余、等边三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
连接,由是⊙O的直径,,得,,由切线的性质得,而,所以,则是等边三角形,所以,由勾股定理得,于是得到问题的答案.
【详解】解:连接,
∵是⊙O的直径,,
∴,,
∵与⊙O相切于点A,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴.
故选:D.
【变式4-3】(2024·海南海口·模拟预测)如图,与相切于点,与弦相交于点,,若,,则的长为 .
【答案】
【分析】本题考查了切线的性质,等腰三角形的判定和性质,余角性质,对顶角的性质,勾股定义,连接,由切线的性质可得,由得,又由得到,即可根据余角性质得到,进而得到,即得到,设,则,,由勾股定理可得,据此即可求解,正确作出辅助线是解题的关键.
【详解】解:连接,如图,
∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
设,则,,
∵,
∴,
解得,
即的长为,
故答案为:.
【题型5 由切线的性质求角度】
【例5】(2024·海南海口·模拟预测)如图,在中,,圆O与交于点D,与相切于点C,,则 .
【答案】/64度
【分析】本题考查圆的切线的性质,圆周角定理、平行线的判定和性质,解题的关键是熟练掌握圆和平行线的相关知识.
根据同弧对应的圆心角是圆周角的2倍计算出,再根据,内错角得到答案.
【详解】解:如图所示,连接,
∵,
∴.
∵是圆的切线
∴,
∵,
∴,
∴,
∴
故答案为:.
【变式5-1】(23-24九年级·重庆九龙坡·开学考试)如图,是的直径,,垂足为E,直线与相切于点C,交于点D,直线交的延长线于点P,连接,若,则的度数是( )
A. B. C. D.
【答案】A
【分析】连接,由切线的性质,可以证明,由平行线的性质、等腰三角形的性质,得到,由,求出的度数,即可得除答案.
【详解】解:连接,
∵与相切于点C,
∴半径,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
故选:A.
【点睛】本题考查了切线的性质、等腰三角形的性质以及平行线的性质,关键是由条件证明.
【变式5-2】(2024九年级·江苏·专题练习)如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
【答案】A
【分析】本题考查正多边形和圆,切线的性质,掌握正六边形的性质,切线的性质以及多边形内角和的计算方法是正确解答的关键.根据正六边形的性质可求出各个内角的度数,由切线的性质以及五边形内角和的计算方法即可求出答案.
【详解】解:∵正六边形的边,与相切于点C,F,
∴,
∵六边形是正六边形,
∴,
在五边形中,
,
故选:A.
【变式5-3】(2024九年级·全国·专题练习)如图分别切于A、B、E,,则( )
A. B. C. D.
【答案】B
【分析】本题考查了切线的性质,三角形全等的判定与性质,四边形的内角和,根据切线的性质证明,,得到,,进而得到,再根据四边形内角和即可求解.
【详解】解:如图,连接,
∵分别切于A、B、E,
,
在与中,
,
,
∴,
同理,
,
∴,
∵,
∴,
∴.
故选:B.
【题型6 利用切线的性质进行证明】
【例6】(2024·山西大同·三模)如图,以的一边为直径作,点恰好落在上,射线与相切于点.
(1)尺规作图:过点作于点,延长交于点,连接;(保留作图痕迹,标明相应字母,不写作法)
(2)在(1)的条件下证明:.
【答案】(1)见解析
(2)见解析
【分析】(1)根据要求作出图形即可;
(2)利用切线的性质结合求得,得到,以及等腰三角形的性质可证,利用圆周角定理得到,据此即可求解.
【详解】(1)解:所作图形如图所示.
(2)解:如图,连接,
∵是的切线,
∴,即,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了作图—作垂线,切线的性质,圆周角定理,平行线的判定和性质,等边对等角等知识,正确引出辅助线解决问题是解题的关键.
【变式6-1】(23-24九年级·福建莆田·期中)如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,根据切线性质,等角对等边,证明.
(2)连接,根据圆的性质,切线的性质,勾股定理解答即可.
本题考查了切线的性质,圆的性质,勾股定理,熟练掌握切线的性质,勾股定理是解题的关键.
【详解】(1)证明:连接,
∵是切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
∴.
(2)解:连接.
∵,
∴,
∵是的直径,,
∴是的切线,
∴,
∴,
∵,
∴,
在中,,
∴,
设,在中,,
在中,,
∴,
解得,
∴.
【变式6-2】(23-24九年级·安徽蚌埠·期末)如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
【答案】(1)
(2)见详解
【分析】(1)根据等腰三角形的性质得到,求得,根据垂径定理得到,于是得到结论;
(2)连接,,根据切线的性质得到,根据平行线的性质得到,根据等腰三角形的性质得到,求得,根据等腰三角形的性质得到,等量代换得到结论.
本题考查了切线的性质,等腰三角形的判定和性质,平行线的判定和性质,圆周角定理,正确地作出辅助线是解题的关键.
【详解】(1)解:,
,
,
是的直径,,
,
,
故的度数为;
(2)证明:连接,,
是的切线,
,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
,
.
【变式6-3】(2024·广东梅州·模拟预测)如图,P为外一点,为的切线,切点分别为A、B,直线交于点D、E,交于点C.
(1)求证∶.
(2)若,连接,求证:四边形是菱形.
【答案】(1)见解析
(2)见解析
【分析】(1)连接,由,证明,,进而得证;
(2)连接,连接,证明,得到,由为的切线得到,,证明,得到,则,得到,又由,即可证明四边形是菱形.
【详解】(1)证明:如图,连接,
∵是直径,
∴
即
∵为的切线,
∴,
即.
∴,
∵
∴,
∴.
(2)连接,连接,如图,
∵,
∴,
∵为的切线,
∴,
∴,
∴
∵为的切线,
∴,,
∵
∴,
∴
∴
∴,
∵,
∴四边形是菱形.
【点睛】此题考查了切线的性质、切线长定理、圆周角定理、全等三角形的判定和性质、菱形的判定等知识,添加适当的辅助线是证明的关键.
【题型7 作圆的切线】
【例7】(2024·江苏镇江·一模)如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上.
(1)的周长为______.
(2)请在如图所示的网格中,用无刻度的直尺在上确定一点,使以点为圆心,以为半径的与相切.(保留作图痕迹)
【答案】(1)12
(2)见解析
【分析】(1)根据勾股定理求出,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质、角平分线的性质、切线的判定定理作图即可.
【详解】(1)解:由勾股定理得:,
则的周长,
故答案为:12;
(2)延长至,使,连接,取的中点,连接交于点,
则点即为所求.
【点睛】本题考查的是勾股定理、切线的判定定理、角平分线的性质、等腰三角形的性质,掌握切线的判定定理是解题的关键.
【变式7-1】(23-24九年级·广东广州·期末)如图,直角梯形中,,,.
(1)尺规作出以为直径的圆(保留作图痕迹,不写作法);
(2)判断与的位置关系,并说明理由.
【答案】(1)见解析
(2)与相切,理由见解析
【分析】(1)根据题意作出线段的垂直平分线,交于点O,然后以O为圆心以为半径画圆即可;
(2)在线段上作,连接,根据题意证明出,然后证明出,进而求解即可.
【详解】(1)如图所示,即为所要求作的以为直径的圆.
(2)在线段上作,连接,,,,
∵,,
∴,
∵,
∴,
∴,,
∵,,
∴,
∴,
∵为圆的直径,
∴点E在上,
∴在和中,
∴,
∴,
∴,
∴与相切.
【点睛】此题考查了垂直平分线的尺规作图,切线的判定,全等三角形的性质和判定等知识,解题的关键是熟练掌握以上知识点.
【变式7-2】(2024·吉林长春·模拟预测)如图,在每个小正方形的边长为1的网格中,的顶点A,B,以为直径的半圆的圆心为O,仅用无刻度的直尺在给定网格中完成画图:
(1)请在图1中作出的边上的高;
(2)请在图2中线段上确定一点F,使得;
(3)请在图3中作出的切线.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】本题考查作图 复杂作图,圆周角定理,切线的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)延长交于点D,连接即可;
(2)利用三角形的三条中线交于一点解决问题即可;
(3)取格点E,连接即可.
【详解】(1)解:如图1中,线段即为所求;
(2)解:如图2中,线段即为所求;
(3)解:如图3中,直线即为所求.
【变式7-3】(2024·山东德州·中考真题)如图,,点、分别在射线、上,,.
(1)用尺规在图中作一段劣弧,使得它在、两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;
(3)求所得的劣弧与线段、围成的封闭图形的面积.
【答案】(1)详见解析;(2)详见解析;(3)
【分析】(1)过、分别作、的垂线,它们相交于,然后以为半径作即可;
(2)写出已知、求证,然后进行证明;连接,先证明,然后根据切线的判定方法判断、为的切线;
(3)先证明为等边三角形得到,,再计算出,然后根据扇形的面积公式,利用劣弧与线段、围成的封闭图形的面积进行计算.
【详解】(1)如图,
(2)已知:如图,,点、分别在射线、上,,,过、分别作、的垂线,它们相交于,以为半径作,,
求证:、为的切线;
证明:∵,,
,
,
连接,
∵,,
,
∵,
,
、为的切线;
(3)∵,
为等边三角形,
,,
∵平分,
,
,
劣弧与线段、围成的封闭图形的面积 .
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了圆周角定理和扇形面积公式.
【题型8 利用切线的判定与性质判断结论正误】
【例8】(2024九年级·安徽·专题练习)如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【答案】A
【分析】由DB=DC,OA=OB,推出OD是△ABC的中位线,OD∥AC,由DF⊥AC,得出DF⊥OD,即DF是☉O的切线,继而证得△ABC是等腰三角形,根据等腰三角形的性质可得∠B=∠C,进而推出△DEC是等腰三角形,进而根据等腰三角形的性质可得CF=EF,由假设推出进而即可求解.
【详解】如图,连接OD,DE,AD,
∵DB=DC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是☉O的切线,故①正确;
∵∠CED+∠AED=180°,∠B+∠AED=180°,
∴∠CED=∠B,
∵AB是☉O的直径,
∴∠ADB=90°,即AD⊥BC,
∵BD=CD,
∴AB=AC,
∴∠B=∠C,
∴∠CED=∠C,
∴DC=DE,
又∵DF⊥AC,
∴CF=EF,故②正确;
当∠EAD=∠EDA时, ,此时△ABC为等边三角形,当△ABC不是等边三角形时,∠EAD≠∠EDA,则
∴不一定正确,
综上,正确结论的序号是①②,
故选A.
【点睛】本题考查切线的判定及其性质,等腰三角形的判定及其性质,圆周角定理、线段垂直平分线的性质,圆内接四边形的性质等知识,综合性较强,解题的关键是熟练掌握并灵活运用所学知识.
【变式8-1】(23-24九年级·安徽合肥·期末)为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
【答案】C
【分析】本题考查了等腰三角形的性质,三角形的外角性质,切线的判定和性质.利用等腰三角形的性质结合三角形的外角性质即可判断选项A、B、D正确;假设成立,证明是等边三角形,推出是的切线,与题设相矛盾,可判断选项C不正确.
【详解】解:连接,
∵平分,
∴设,
若,
∴,
则,选项A正确,不符合题意;
若,又∵,
∴,
∴,选项B正确,不符合题意;
若切于点,
∴,即,
∴,
∵,
∴,
∴,选项D正确,不符合题意;
连接,假设成立,
∵为的直径,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴点在以为直径的圆上,即,
∴切于点,
而题设并没有是的切线这一条件,
∴假设不成立,选项C不正确,符合题意.
故选:C.
【变式8-2】(2014·江苏无锡·中考真题)如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
【答案】A
【详解】解:连接OD,
∵CD是⊙O的切线,
∴CD⊥OD,
∴∠ODC=90°,
又∵∠A=30°,
∴∠ABD=60°,
又∵OB=OD,
∴△OBD是等边三角形.
∴∠DOB=∠ABD=60°,AB=2OB=2OD=2BD.
∴∠C=∠BDC=30°.
∴BD=BC,②成立.
∴AB=2BC,③成立.
∴∠A=∠C.
∴DA=DC,①成立.
综上所述,①②③均成立.
故选:A.
【点睛】本题考查切线的性质;直角三角形两锐角的关系;等边三角形的判定和性质;等腰三角形的判定.
【变式8-3】(23-24九年级·河北保定·期中)在黑板上有如下内容:“如图,是半圆所在圆的直径,,点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目,下列判断正确的是( )
嘉嘉:若给出,则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且,则可求出的面积.
A.只有嘉嘉的正确 B.只有淇淇的正确
C.嘉嘉和淇淇的都不正确 D.嘉嘉和淇淇的都正确
【答案】D
【分析】根据切线的求证方法,如图所示(见详解),连接,证明即可求解;根据切线的性质,,可求出等腰三角形,等边三角形,根据含特殊角的直角三角形的直线可求出各边的长度,由此即可求解.
【详解】解:∵是半圆所在圆的直径,
∴,
如图所示,连接,
∵是半径,
∴,
∵,
∴,
嘉嘉给出的条件是:,
∴,即,且点在圆上,
∴直线是半圆的切线,故嘉嘉给出的条件正确;
淇淇给出的条件:直线是的切线,且,如图所示,
∴,且是等腰三角形,
∴,
∴,
∵,,
∴,且,
∴是等边三角形,
∴,
∵,
∴,
∴,
如图所示,过点作于,
在是等边三角形,,
∴,故淇淇给出的条件正确,
故选:.
【点睛】本题主要考查圆与特殊角的直角三角形的综合,掌握圆切线的求证方法,含特殊角的直角三角形的性质,等边三角形的性质是解题的关键.
【题型9 利用切线的判定与性质进行求值或证明】
【例9】(23-24九年级·黑龙江哈尔滨·阶段练习)如图,中,,点在边上,过点且分别与边、相交于、两点,,点为垂足.
(1)求证:直线是的切线;
(2)当是等边三角形,且直线与相切时,直接写出长度为线段长度2倍的所有线段.
【答案】(1)见解析
(2)长度为线段长度2倍的所有线段有:,,,.
【分析】(1)利用等腰三角形的性质,同圆的半径相等,平行线的判定与性质和圆的切线的判定定理解答即可;
(2)连接,利用圆周角定理和含角的直角三角形的性质,得到;再利用圆的切线的性质定理,等边三角形的性质和直角三角形的性质,全等三角形的判定与性质解答即可得出结论.
【详解】(1)证明:连接,如图,
,
.
,
,
,
.
,
,
为的半径,
直线是的切线;
(2)解:连接,如图,
为的直径,
,
是等边三角形,
,
,
.
,
,
.
直线与相切,
,
,
,
为等边三角形,
.
在和中,
,
,
.
同理:,
.
.
由题意:,
,
,
长度为线段长度2倍的所有线段有:,,,.
【点睛】本题主要考查了等腰三角形的性质,等边三角形的性质,圆的有关性质,圆的切线的判定,圆周角定理,全等三角形的判定与性质,含角的直角三角形的性质,连接经过切点的半径是解决此类问题常添加的辅助线.
【变式9-1】(2024·辽宁沈阳·二模)如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点,且,连接.
(1)求证:是的切线;
(2)若,,求的半径的长.
【答案】(1)证明见解析
(2)
【分析】本题主要考查了切线的性质与判定, 等弧所对的圆心角相等,全等三角形的性质与判定,勾股定理等等:
(1)如图所示,连接,由切线的性质得到,再由得到,证明,得到,据此可证明结论;
(2)设的半径为r,则,在中利用勾股定理建立方程求解即可.
【详解】(1)证明:如图所示,连接,
∵与相切于点B,
∴ ,
∵,
∴,
又∵,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解:设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为.
【变式9-2】(2024·陕西西安·模拟预测)如图,在中,以边上一点O为圆心,为半径作,与相切于点A.作交的延长线于点D,且.
(1)求证:是的切线;
(2)若,,求⊙O的半径.
【答案】(1)见解析
(2)
【分析】(1)过O点作于点E,推导出,然后根据角平分线的性质即可得到,证明结论;
(2)先利用勾股定理求出长,然后利用全等三角形得到,然后再在中利用勾股定理解题即可.
【详解】(1)证明:过O点作于点E,
∵与相切于点A,
∴
又∵,
∴,
∵,
∴,
又∵,,
∴,
∴是的切线;
(2)解:∵,,
∴,
在和中,
,
∴,
∴,
∴,
在中,,即,
解得:.
【点睛】本题考查切线的判定与性质,角平分线的性质,勾股定理,全等三角形的判定与性质,解题的关键是掌握切线的判定和性质.
【变式9-3】(23-24九年级·广东·单元测试)如图1,为直径,与相切于点B,D为上一点,连接,若.
(1)求证:为的切线;
(2)如图2,过点A作交延长线于点E,连接交于点F,若,求的长.
【答案】(1)详见解析
(2)
【分析】(1)连接,由切线的性质得出,证明,由全等三角形的性质得出,则可得出结论;
(2)设,根据切线长定理可得,过点E作于M,可得,由勾股定理求出,求出的长,则可得出答案.
【详解】(1)证明:连接,
∵与相切,
∴,即,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
又为半径,
∴为的切线;
(2)解:如图,连接,
设,
∵,
∴,
∵,
∴为的切线,
∵为的切线,
∴,,
∴,
∵,
∴垂直平分,
∴,
过点E作于M,则,
∴四边形是矩形,
∴,
∴,
在中,,
∴,解得,
∴,
∴,
∵,
∴.
【点睛】此题主要考查了切线的判定和性质、全等三角形的判定和性质、勾股定理、切线长定理等知识的综合应用,是一道综合性较强的题目.
【题型10 切线的应用】
【例10】(2024·福建宁德·二模)综合与实践:
任务一:确定弦的长度.如图2,求所对弦的长度.
任务二:设计甲组扇面.如图3,已知甲组的圆形卡纸直径为.请运用所给工具在中设计与图2相同的扇面,并标出相应数据.
任务三:确定卡纸大小.如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2,扇面形状为扇环,且,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【答案】任务一:, 任务二:见解析;任务三:矩形的边长为、.
【分析】本题考查了垂径定理,含角的直角三角形,解题的关键是:熟练掌握相关性质定理.
任务一:由弧所对的圆心角为,可得,求得,应用勾股定理求出,即可求解,
任务二:以直径为底边,构造底角为30度的等腰三角形,则得到的三角形和任务一三角形全等,再按要求取点,再以为圆心,分别以、为半径画弧,得到的扇面图形与图2相同;
任务三:在上取一点使,以为圆心,为半径的圆与相切,此时点与点重合,在圆上取一点A,使,即可得到扇面.过点作,则矩形为最小规格矩形,
【详解】任务一:解:过点O作,交于点,
,,
,
,
,,
,
任务二:如图,是以直径为底边,底角为度,由任务一可知,,取,以O为圆心,分别以、为半径画弧,即可得到扇面.
任务三:如图所示:当与矩形两边相切时,过点作,则矩形为最小规格矩形,
∵,,,
∴,,,
∵当与矩形两边相切,
∴最小规格矩形的边长为、,
【变式10-1】(23-24九年级·浙江杭州·)图1是一种推磨工具模型,图2是它的示意图,已知,,点A在中轴线上运动,点B在以O为圆心,长为半径的圆上运动,且,如图3,当点B按逆时针方向运动到时,与相切,则 .
【答案】
【分析】由题意得到A′A=OA-OA′=AB+OB-OA′,即可求解.
【详解】解:由题意可得:
A′A=OA-OA′=AB+OB-OA′=12+4-==,
故答案为:.
【点睛】本题考查的是切线的性质,勾股定理,解题的关键是确定转动后图形重要点的位置关系.
【变式10-2】(2024·河北邯郸·模拟预测)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具.图1,图2是某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,是粒子真空室,C、D是两个加速电极,高速飞行的粒子J在A点注入,在粒子真空室内做环形运动,每次经过 时被加速,达到一定的速度在B点引出,粒子注入和引出路径都与相切.已知:,粒子注入路径与夹角,所对的圆心角是.
(1)求的度数;
(2)通过计算,比较与的长度哪个更长;
(3)直接写出粒子J在环形运动过程中,粒子J到的最远距离.(相关数据: )
【答案】(1)
(2)的长度更长,见解析
(3)粒子J到的最远距离是
【分析】(1)如图,延长交于G,根据切线长定理和等腰三角形的性质即可得到结论;
(2)根据弧长公式求出的长,再进行比较即可;
(3)如图,当粒子J运动到P点时,离的距离最远,根据切线的性质得到,再根据垂径定理和三角函数得出的长,进而解答即可
【详解】(1)解:如图,延长交于G,
由题意得,是的切线,
∴,
∴;
(2)解:的长度更长,
∵所对的圆心角为,,
∴的长度约为,
∵,
∴的长度更长;
(3)解:如图,过点O作于点E,延长交于点P,连接,
∵是的切线,
∴,
∵,
∴,
∵是的弦,是弦心距,,
∴,,
∴,
∴,
∴,
如图,当粒子J运动到P点时,离的距离最远,
∴,
即粒子J到的最远距离是.
【点睛】本题是圆的综合题,涉及圆周角定理,圆切线的性质,垂径定理,解直角三角形,弧长公式,正确作出辅助线是解题关键.
【变式10-3】(2013·浙江温州·中考真题)一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线切割,如图1所示.图2中的矩形是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则的长分别是 .
【答案】18cm, 31cm.
【分析】如图,延长交线段于点,延长交于点G,交于点,设圆孔半径为r.根据勾股定理,得.从而得.根据题意知,.则根据图中相关线段间的和差关系求得CN=QH-QN2=44-26=18, AM=BC-PD-KM1=130-50-49=31 ( cm).
【详解】解:作辅助线如图所示,设圆孔半径为r,
根据勾股定理,得.
∴,
.
按题意要求,切割后,以圆O为中心,到两对边的距离相等,
即:.
∵,
∴ QN2+r=42,即QN2=42-16=26.
∴CN=QH-QN2=44-26=18.
又∵,即 ,
∴ KM1=49.
∴AM=BC-PD-KM1=130-50-49=31.
∴CN=18cm,AM=31cm.
故答案为:18cm,31cm
【点睛】本题考查了矩形、直角三角形及圆等相关知识,将实际问题转化为数学问题经验,利用图形变换思想是解题的关键,体现了数学思想方法在现实问题中的应用价值.
21世纪教育网(www.21cnjy.com)
同课章节目录
