2023-2024学年广东省东莞市光明中学八年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省东莞市光明中学八年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 675.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 17:57:11 | ||
图片预览


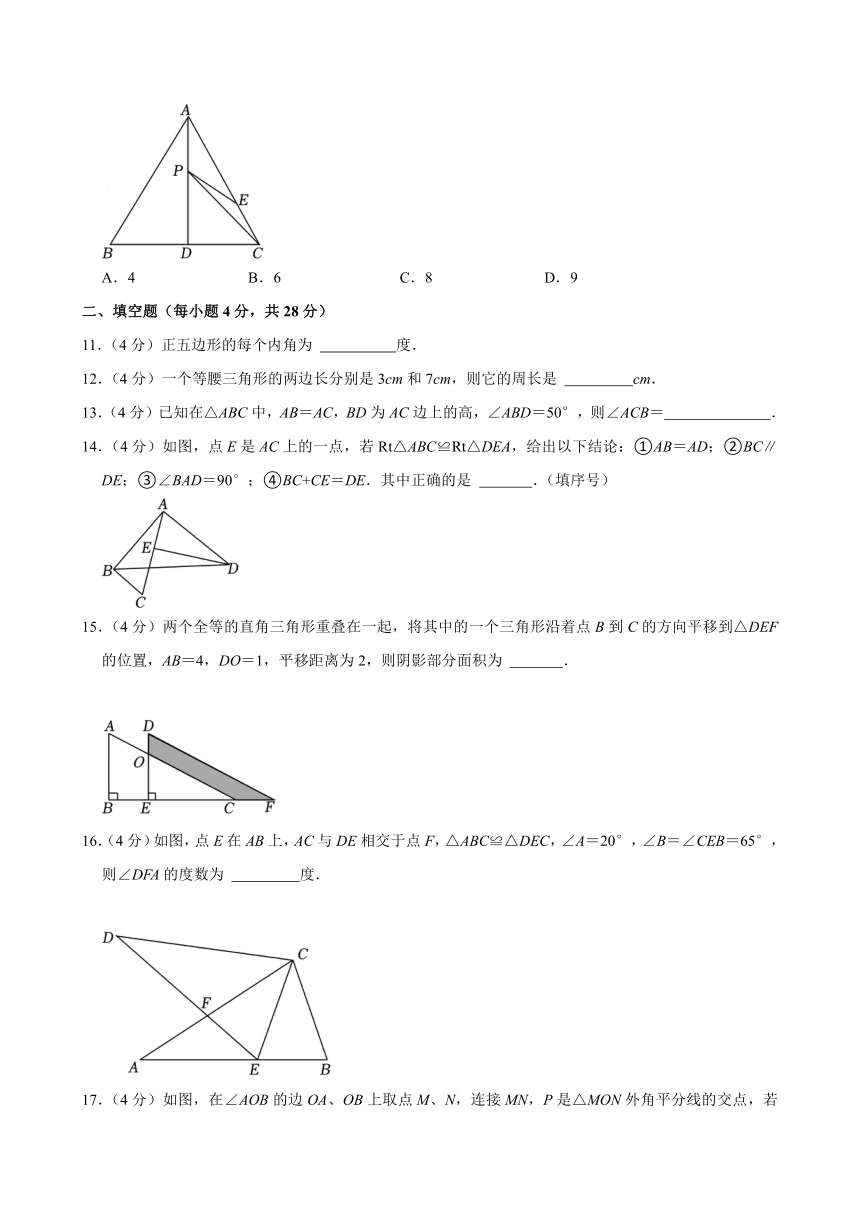
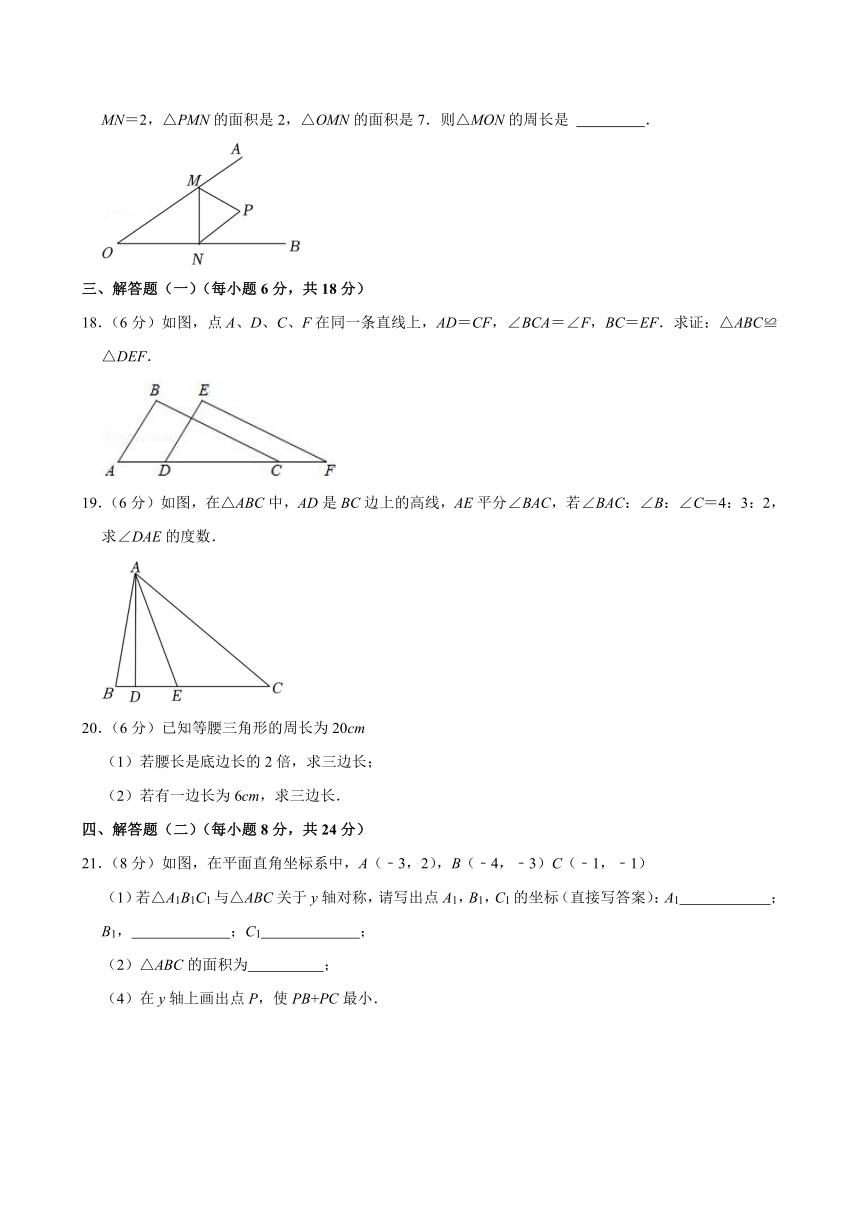
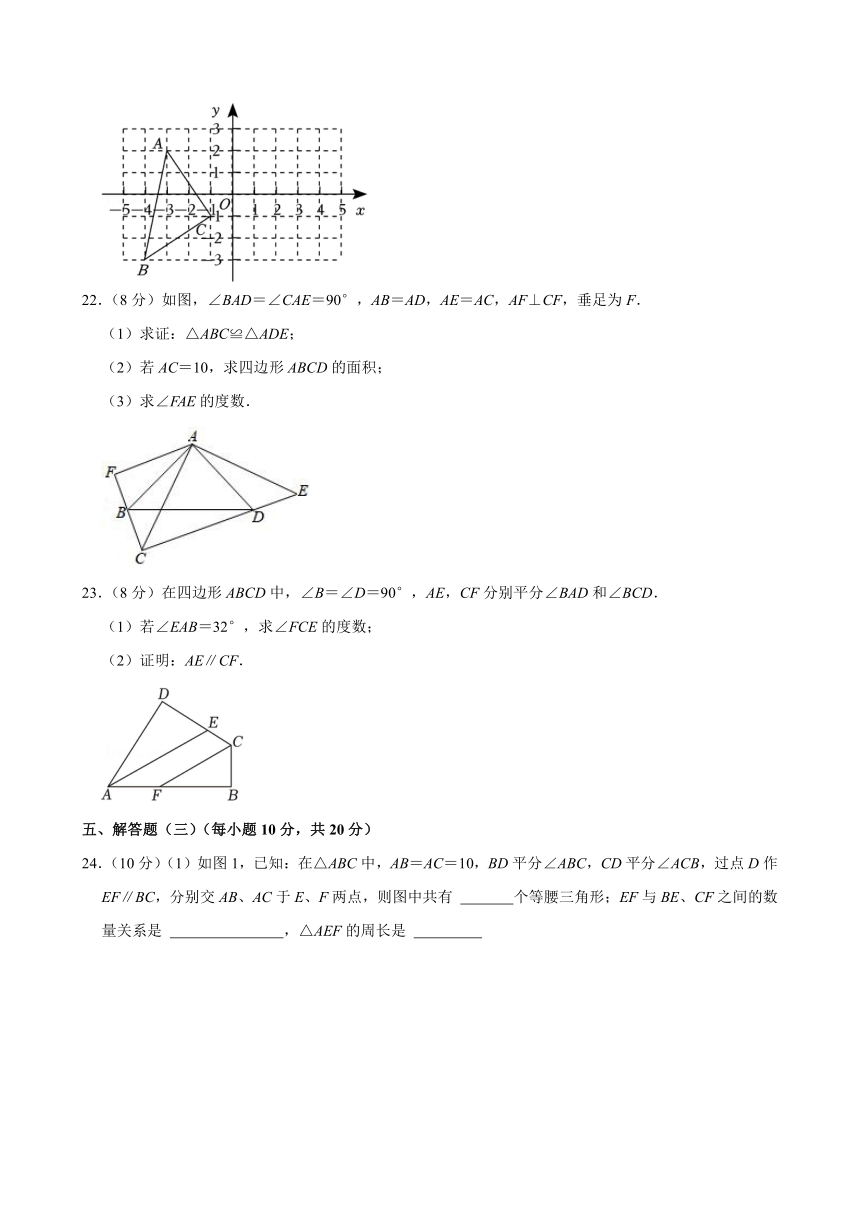
文档简介
2023-2024学年广东省东莞市光明中学八年级(上)期中数学试卷
一、选择题(每小题3分,共30分)
1.(3分)下列图形中,不是轴对称图形的是( )
A. B.
C. D.
2.(3分)下列几组数中,不能作为三角形的三边长的是( )
A.6,6,6 B.1,5,5 C.3,4,5 D.2,4,6
3.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
4.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A=∠B=3∠C B.∠A+∠B=∠C
C. D.∠A:∠B:∠C=1:2:3
5.(3分)下面四个图形中,画出△ABC的边BC上的高正确的是( )
A. B.
C. D.
6.(3分)如图,在△ABC中,∠A=60°,∠B=48°,CD平分∠ACB交AB于点D,则∠BDC的大小为( )
A.72° B.90° C.96° D.108°
7.(3分)将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
8.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
9.(3分)如图,将两根同样的钢条AC和BD的中点O固定在一起,使其可以绕着O点自由转动,就做成了一个测量工件内径的工具.这时根据△OAB≌△OCD,CD的长就等于工件内槽的宽AB,这里判定△OAB≌△OCD的依据是( )
A.SAS B.ASA C.SSS D.AAS
10.(3分)如图,等边△ABC中,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于( )
A.4 B.6 C.8 D.9
二、填空题(每小题4分,共28分)
11.(4分)正五边形的每个内角为 度.
12.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 cm.
13.(4分)已知在△ABC中,AB=AC,BD为AC边上的高,∠ABD=50°,则∠ACB= .
14.(4分)如图,点E是AC上的一点,若Rt△ABC≌Rt△DEA,给出以下结论:①AB=AD;②BC∥DE;③∠BAD=90°;④BC+CE=DE.其中正确的是 .(填序号)
15.(4分)两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2,则阴影部分面积为 .
16.(4分)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为 度.
17.(4分)如图,在∠AOB的边OA、OB上取点M、N,连接MN,P是△MON外角平分线的交点,若MN=2,△PMN的面积是2,△OMN的面积是7.则△MON的周长是 .
三、解答题(一)(每小题6分,共18分)
18.(6分)如图,点A、D、C、F在同一条直线上,AD=CF,∠BCA=∠F,BC=EF.求证:△ABC≌△DEF.
19.(6分)如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
20.(6分)已知等腰三角形的周长为20cm
(1)若腰长是底边长的2倍,求三边长;
(2)若有一边长为6cm,求三边长.
四、解答题(二)(每小题8分,共24分)
21.(8分)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3)C(﹣1,﹣1)
(1)若△A1B1C1与△ABC关于y轴对称,请写出点A1,B1,C1的坐标(直接写答案):A1 ;B1, ;C1 ;
(2)△ABC的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.
22.(8分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
(1)求证:△ABC≌△ADE;
(2)若AC=10,求四边形ABCD的面积;
(3)求∠FAE的度数.
23.(8分)在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD和∠BCD.
(1)若∠EAB=32°,求∠FCE的度数;
(2)证明:AE∥CF.
五、解答题(三)(每小题10分,共20分)
24.(10分)(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有 个等腰三角形;EF与BE、CF之间的数量关系是 ,△AEF的周长是
(2)如图2,若将(1)中“△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有 个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
25.(10分)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)线段AP的长为 (用含t的式子表示).
(2)请判断AB与DE的数量与位置关系,并证明你的结论.
(3)连接PQ,当线段PQ经过点C时,求t的值.
2023-2024学年广东省东莞市光明中学八年级(上)期中数学试卷
参考答案
一、选择题(每小题3分,共30分)
1.(3分)下列图形中,不是轴对称图形的是( )
A. B.
C. D.
选:C.
2.(3分)下列几组数中,不能作为三角形的三边长的是( )
A.6,6,6 B.1,5,5 C.3,4,5 D.2,4,6
选:D.
3.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
选:C.
4.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A=∠B=3∠C B.∠A+∠B=∠C
C. D.∠A:∠B:∠C=1:2:3
选:A.
5.(3分)下面四个图形中,画出△ABC的边BC上的高正确的是( )
A. B.
C. D.
选:C.
6.(3分)如图,在△ABC中,∠A=60°,∠B=48°,CD平分∠ACB交AB于点D,则∠BDC的大小为( )
A.72° B.90° C.96° D.108°
选:C.
7.(3分)将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
选:A.
8.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
选:C.
9.(3分)如图,将两根同样的钢条AC和BD的中点O固定在一起,使其可以绕着O点自由转动,就做成了一个测量工件内径的工具.这时根据△OAB≌△OCD,CD的长就等于工件内槽的宽AB,这里判定△OAB≌△OCD的依据是( )
A.SAS B.ASA C.SSS D.AAS
选:A.
10.(3分)如图,等边△ABC中,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于( )
A.4 B.6 C.8 D.9
选:A.
二、填空题(每小题4分,共28分)
11.(4分)正五边形的每个内角为 108 度.
12.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 17 cm.
13.(4分)已知在△ABC中,AB=AC,BD为AC边上的高,∠ABD=50°,则∠ACB= 70°或20° .
14.(4分)如图,点E是AC上的一点,若Rt△ABC≌Rt△DEA,给出以下结论:①AB=AD;②BC∥DE;③∠BAD=90°;④BC+CE=DE.其中正确的是 ③ .(填序号)
15.(4分)两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2,则阴影部分面积为 7 .
16.(4分)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为 70 度.
17.(4分)如图,在∠AOB的边OA、OB上取点M、N,连接MN,P是△MON外角平分线的交点,若MN=2,△PMN的面积是2,△OMN的面积是7.则△MON的周长是 11 .
三、解答题(一)(每小题6分,共18分)
18.(6分)如图,点A、D、C、F在同一条直线上,AD=CF,∠BCA=∠F,BC=EF.求证:△ABC≌△DEF.
【解答】证明:∵AD=CF,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
19.(6分)如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
【解答】解:在△ABC中,
∵∠BAC:∠B:∠C=4:3:2,
∴∠BAC=180°×=80°,∠B=180°×=60°,
∵AD是BC边上的高线,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°.
20.(6分)已知等腰三角形的周长为20cm
(1)若腰长是底边长的2倍,求三边长;
(2)若有一边长为6cm,求三边长.
【解答】解:(1)设底边长x cm,则腰长为2x cm.
x+2x+2x=20,
解得 x=4
∴腰长=2x=2×4=8 (cm);
(2)因为长为 6cm的边可能是腰,也可能是底,所以要分两种情况计算:
①6cm是底,设腰为y的情况:2y+6=20,y=7,符合三角形三边关系.
②6cm是腰,设底为m的情况:2×6+m=20,m=8,符合三角形三边关系.
故三边长为6cm,7cm,7cm或6cm,6cm,8cm.
四、解答题(二)(每小题8分,共24分)
21.(8分)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3)C(﹣1,﹣1)
(1)若△A1B1C1与△ABC关于y轴对称,请写出点A1,B1,C1的坐标(直接写答案):A1 (3,2) ;B1, (4,﹣3) ;C1 (1,﹣1) ;
(2)△ABC的面积为 6.5 ;
(4)在y轴上画出点P,使PB+PC最小.
【解答】解:(1)如图所示,△A1B1C1即为所求,
A1(3,2)、B1(4,﹣3)、C1(1,﹣1),
故答案为:(3,2)、(4,﹣3)、(1,﹣1);
(2)△ABC的面积为3×5﹣×1×5﹣×2×3﹣×2×3=6.5,
故答案为:6.5;
(3)如图所示,点P即为所求.
22.(8分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
(1)求证:△ABC≌△ADE;
(2)若AC=10,求四边形ABCD的面积;
(3)求∠FAE的度数.
【解答】证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAD﹣∠CAD=∠CAE﹣∠CAD,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS);
(2)∵△ABC≌△ADE,
∴S△ABC=S△ADE,
∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD=S△ACE,
∵AC=AE=10,
∴S四边形ABCD=S△ACE=×10×10=50;
(3)∵∠CAE=90°,AC=AE,
∴∠E=45°,
∵△ABC≌△ADE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CAF=∠FCA=45°,
∴∠FAE=135°.
23.(8分)在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD和∠BCD.
(1)若∠EAB=32°,求∠FCE的度数;
(2)证明:AE∥CF.
【解答】(1)解:∵AE、CF分别平分∠BAD和∠BCD,∠EAB=32°,
∴∠DAB=64°,
∵∠B=∠D=90°,
∴∠DAB+∠DCB=180°,
∴∠DCB=180°﹣∠DAB=116°,
∴;
(2)证明:∵∠B=∠D=90°,
∴∠DAB+∠DCB=180°,∠CFB+∠FCB=90°,
∵AE平分∠BAD交CD于点E,CF平分∠BCD交AB于点F,
∴,
∴∠CFB=∠EAB,
∴AE∥CF.
五、解答题(三)(每小题10分,共20分)
24.(10分)(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有 5 个等腰三角形;EF与BE、CF之间的数量关系是 BE+CF=EF ,△AEF的周长是 20
(2)如图2,若将(1)中“△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有 2 个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
【解答】解:(1)BE+CF=EF.
理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∴∠DBC=∠DCB,
∴DB=DC
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,AE=AF,
∴等腰三角形有△ABC,△AEF,△DEB,△DFC,△BDC共5个,
∴BE+CF=DE+DF=EF,
即BE+CF=EF,
△AEF的周长=AE+EF+AF=AE+BE+AF+FC=AB+AC=20.
故答案为:5;BE+CF=EF;20;
(2)BE+CF=EF,
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,
∴BE+CF=DE+DF=EF,即BE+CF=EF.
可得△AEF的周长为18.
(3)BE﹣CF=EF,
由(1)知BE=ED,
∵EF∥BC,
∴∠EDC=∠DCG=∠ACD,
∴CF=DF,
又∵ED﹣DF=EF,
∴BE﹣CF=EF.
25.(10分)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)线段AP的长为 3t cm或(8﹣3t)cm (用含t的式子表示).
(2)请判断AB与DE的数量与位置关系,并证明你的结论.
(3)连接PQ,当线段PQ经过点C时,求t的值.
【解答】解:(1)当0≤t≤时,AP=3t cm;
当<t≤时,BP=(3t﹣4)cm,
则AP=4﹣(3t﹣4)=(8﹣3t)cm;
综上所述,线段AP的长为3t cm或(8﹣3t)cm,
故答案为:3t cm或(8﹣3t)cm;
(2)AB=DE,AB∥DE,理由如下:
在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,AB=DE,
∴AB∥DE;
(3)由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4﹣t,
解得:t=1;
当<t≤时,8﹣3t=4﹣t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1或2,
一、选择题(每小题3分,共30分)
1.(3分)下列图形中,不是轴对称图形的是( )
A. B.
C. D.
2.(3分)下列几组数中,不能作为三角形的三边长的是( )
A.6,6,6 B.1,5,5 C.3,4,5 D.2,4,6
3.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
4.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A=∠B=3∠C B.∠A+∠B=∠C
C. D.∠A:∠B:∠C=1:2:3
5.(3分)下面四个图形中,画出△ABC的边BC上的高正确的是( )
A. B.
C. D.
6.(3分)如图,在△ABC中,∠A=60°,∠B=48°,CD平分∠ACB交AB于点D,则∠BDC的大小为( )
A.72° B.90° C.96° D.108°
7.(3分)将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
8.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
9.(3分)如图,将两根同样的钢条AC和BD的中点O固定在一起,使其可以绕着O点自由转动,就做成了一个测量工件内径的工具.这时根据△OAB≌△OCD,CD的长就等于工件内槽的宽AB,这里判定△OAB≌△OCD的依据是( )
A.SAS B.ASA C.SSS D.AAS
10.(3分)如图,等边△ABC中,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于( )
A.4 B.6 C.8 D.9
二、填空题(每小题4分,共28分)
11.(4分)正五边形的每个内角为 度.
12.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 cm.
13.(4分)已知在△ABC中,AB=AC,BD为AC边上的高,∠ABD=50°,则∠ACB= .
14.(4分)如图,点E是AC上的一点,若Rt△ABC≌Rt△DEA,给出以下结论:①AB=AD;②BC∥DE;③∠BAD=90°;④BC+CE=DE.其中正确的是 .(填序号)
15.(4分)两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2,则阴影部分面积为 .
16.(4分)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为 度.
17.(4分)如图,在∠AOB的边OA、OB上取点M、N,连接MN,P是△MON外角平分线的交点,若MN=2,△PMN的面积是2,△OMN的面积是7.则△MON的周长是 .
三、解答题(一)(每小题6分,共18分)
18.(6分)如图,点A、D、C、F在同一条直线上,AD=CF,∠BCA=∠F,BC=EF.求证:△ABC≌△DEF.
19.(6分)如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
20.(6分)已知等腰三角形的周长为20cm
(1)若腰长是底边长的2倍,求三边长;
(2)若有一边长为6cm,求三边长.
四、解答题(二)(每小题8分,共24分)
21.(8分)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3)C(﹣1,﹣1)
(1)若△A1B1C1与△ABC关于y轴对称,请写出点A1,B1,C1的坐标(直接写答案):A1 ;B1, ;C1 ;
(2)△ABC的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.
22.(8分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
(1)求证:△ABC≌△ADE;
(2)若AC=10,求四边形ABCD的面积;
(3)求∠FAE的度数.
23.(8分)在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD和∠BCD.
(1)若∠EAB=32°,求∠FCE的度数;
(2)证明:AE∥CF.
五、解答题(三)(每小题10分,共20分)
24.(10分)(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有 个等腰三角形;EF与BE、CF之间的数量关系是 ,△AEF的周长是
(2)如图2,若将(1)中“△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有 个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
25.(10分)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)线段AP的长为 (用含t的式子表示).
(2)请判断AB与DE的数量与位置关系,并证明你的结论.
(3)连接PQ,当线段PQ经过点C时,求t的值.
2023-2024学年广东省东莞市光明中学八年级(上)期中数学试卷
参考答案
一、选择题(每小题3分,共30分)
1.(3分)下列图形中,不是轴对称图形的是( )
A. B.
C. D.
选:C.
2.(3分)下列几组数中,不能作为三角形的三边长的是( )
A.6,6,6 B.1,5,5 C.3,4,5 D.2,4,6
选:D.
3.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
选:C.
4.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A=∠B=3∠C B.∠A+∠B=∠C
C. D.∠A:∠B:∠C=1:2:3
选:A.
5.(3分)下面四个图形中,画出△ABC的边BC上的高正确的是( )
A. B.
C. D.
选:C.
6.(3分)如图,在△ABC中,∠A=60°,∠B=48°,CD平分∠ACB交AB于点D,则∠BDC的大小为( )
A.72° B.90° C.96° D.108°
选:C.
7.(3分)将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
选:A.
8.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
选:C.
9.(3分)如图,将两根同样的钢条AC和BD的中点O固定在一起,使其可以绕着O点自由转动,就做成了一个测量工件内径的工具.这时根据△OAB≌△OCD,CD的长就等于工件内槽的宽AB,这里判定△OAB≌△OCD的依据是( )
A.SAS B.ASA C.SSS D.AAS
选:A.
10.(3分)如图,等边△ABC中,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于( )
A.4 B.6 C.8 D.9
选:A.
二、填空题(每小题4分,共28分)
11.(4分)正五边形的每个内角为 108 度.
12.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 17 cm.
13.(4分)已知在△ABC中,AB=AC,BD为AC边上的高,∠ABD=50°,则∠ACB= 70°或20° .
14.(4分)如图,点E是AC上的一点,若Rt△ABC≌Rt△DEA,给出以下结论:①AB=AD;②BC∥DE;③∠BAD=90°;④BC+CE=DE.其中正确的是 ③ .(填序号)
15.(4分)两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2,则阴影部分面积为 7 .
16.(4分)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为 70 度.
17.(4分)如图,在∠AOB的边OA、OB上取点M、N,连接MN,P是△MON外角平分线的交点,若MN=2,△PMN的面积是2,△OMN的面积是7.则△MON的周长是 11 .
三、解答题(一)(每小题6分,共18分)
18.(6分)如图,点A、D、C、F在同一条直线上,AD=CF,∠BCA=∠F,BC=EF.求证:△ABC≌△DEF.
【解答】证明:∵AD=CF,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
19.(6分)如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
【解答】解:在△ABC中,
∵∠BAC:∠B:∠C=4:3:2,
∴∠BAC=180°×=80°,∠B=180°×=60°,
∵AD是BC边上的高线,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°.
20.(6分)已知等腰三角形的周长为20cm
(1)若腰长是底边长的2倍,求三边长;
(2)若有一边长为6cm,求三边长.
【解答】解:(1)设底边长x cm,则腰长为2x cm.
x+2x+2x=20,
解得 x=4
∴腰长=2x=2×4=8 (cm);
(2)因为长为 6cm的边可能是腰,也可能是底,所以要分两种情况计算:
①6cm是底,设腰为y的情况:2y+6=20,y=7,符合三角形三边关系.
②6cm是腰,设底为m的情况:2×6+m=20,m=8,符合三角形三边关系.
故三边长为6cm,7cm,7cm或6cm,6cm,8cm.
四、解答题(二)(每小题8分,共24分)
21.(8分)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3)C(﹣1,﹣1)
(1)若△A1B1C1与△ABC关于y轴对称,请写出点A1,B1,C1的坐标(直接写答案):A1 (3,2) ;B1, (4,﹣3) ;C1 (1,﹣1) ;
(2)△ABC的面积为 6.5 ;
(4)在y轴上画出点P,使PB+PC最小.
【解答】解:(1)如图所示,△A1B1C1即为所求,
A1(3,2)、B1(4,﹣3)、C1(1,﹣1),
故答案为:(3,2)、(4,﹣3)、(1,﹣1);
(2)△ABC的面积为3×5﹣×1×5﹣×2×3﹣×2×3=6.5,
故答案为:6.5;
(3)如图所示,点P即为所求.
22.(8分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
(1)求证:△ABC≌△ADE;
(2)若AC=10,求四边形ABCD的面积;
(3)求∠FAE的度数.
【解答】证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAD﹣∠CAD=∠CAE﹣∠CAD,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS);
(2)∵△ABC≌△ADE,
∴S△ABC=S△ADE,
∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD=S△ACE,
∵AC=AE=10,
∴S四边形ABCD=S△ACE=×10×10=50;
(3)∵∠CAE=90°,AC=AE,
∴∠E=45°,
∵△ABC≌△ADE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CAF=∠FCA=45°,
∴∠FAE=135°.
23.(8分)在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD和∠BCD.
(1)若∠EAB=32°,求∠FCE的度数;
(2)证明:AE∥CF.
【解答】(1)解:∵AE、CF分别平分∠BAD和∠BCD,∠EAB=32°,
∴∠DAB=64°,
∵∠B=∠D=90°,
∴∠DAB+∠DCB=180°,
∴∠DCB=180°﹣∠DAB=116°,
∴;
(2)证明:∵∠B=∠D=90°,
∴∠DAB+∠DCB=180°,∠CFB+∠FCB=90°,
∵AE平分∠BAD交CD于点E,CF平分∠BCD交AB于点F,
∴,
∴∠CFB=∠EAB,
∴AE∥CF.
五、解答题(三)(每小题10分,共20分)
24.(10分)(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有 5 个等腰三角形;EF与BE、CF之间的数量关系是 BE+CF=EF ,△AEF的周长是 20
(2)如图2,若将(1)中“△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有 2 个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
【解答】解:(1)BE+CF=EF.
理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∴∠DBC=∠DCB,
∴DB=DC
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,AE=AF,
∴等腰三角形有△ABC,△AEF,△DEB,△DFC,△BDC共5个,
∴BE+CF=DE+DF=EF,
即BE+CF=EF,
△AEF的周长=AE+EF+AF=AE+BE+AF+FC=AB+AC=20.
故答案为:5;BE+CF=EF;20;
(2)BE+CF=EF,
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,
∴BE+CF=DE+DF=EF,即BE+CF=EF.
可得△AEF的周长为18.
(3)BE﹣CF=EF,
由(1)知BE=ED,
∵EF∥BC,
∴∠EDC=∠DCG=∠ACD,
∴CF=DF,
又∵ED﹣DF=EF,
∴BE﹣CF=EF.
25.(10分)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)线段AP的长为 3t cm或(8﹣3t)cm (用含t的式子表示).
(2)请判断AB与DE的数量与位置关系,并证明你的结论.
(3)连接PQ,当线段PQ经过点C时,求t的值.
【解答】解:(1)当0≤t≤时,AP=3t cm;
当<t≤时,BP=(3t﹣4)cm,
则AP=4﹣(3t﹣4)=(8﹣3t)cm;
综上所述,线段AP的长为3t cm或(8﹣3t)cm,
故答案为:3t cm或(8﹣3t)cm;
(2)AB=DE,AB∥DE,理由如下:
在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,AB=DE,
∴AB∥DE;
(3)由(1)得:∠A=∠E,ED=AB=4cm,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4﹣t,
解得:t=1;
当<t≤时,8﹣3t=4﹣t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1或2,
同课章节目录
