2024-2025学年高一数学苏教版必修一课时作业 7.1 角与弧度(含解析)
文档属性
| 名称 | 2024-2025学年高一数学苏教版必修一课时作业 7.1 角与弧度(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 11:35:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年高一数学苏教版必修一课时作业 7.1 角与弧度
一、选择题
1.下列选项中,与角终边相同的角是( )
A. B. C. D.
2.下列各角中与终边相同的角为( )
A. B. C. D.
3.与角终边相同的角是( )
A. B. C. D.
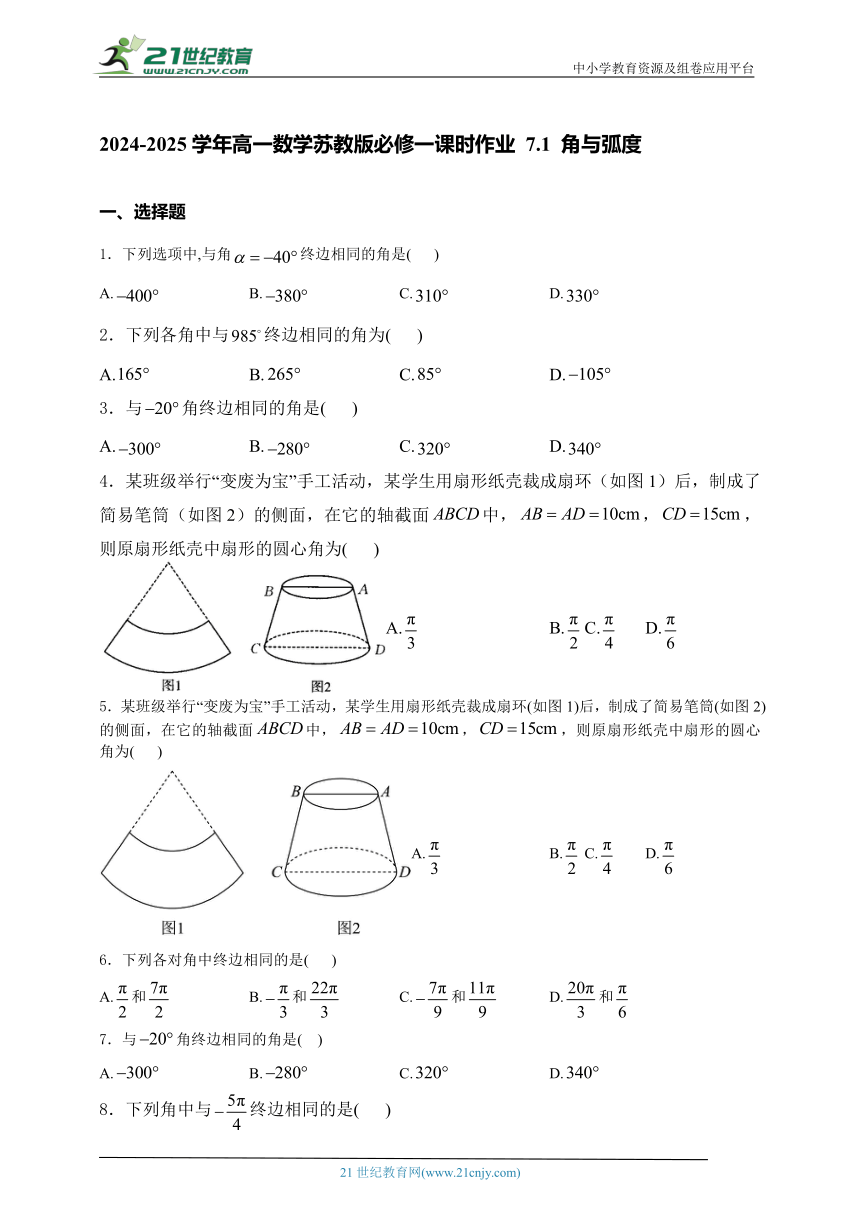
4.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面中,,,则原扇形纸壳中扇形的圆心角为( )
A. B. C. D.
5.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面中,,,则原扇形纸壳中扇形的圆心角为( )
A. B. C. D.
6.下列各对角中终边相同的是( )
A.和 B.和 C.和 D.和
7.与角终边相同的角是( )
A. B. C. D.
8.下列角中与终边相同的是( )
A. B. C. D.
二、多项选择题
9.已知角与的终边相同,则角可以是( )
A. B. C. D.
10.高一某班的同学在学习了任意角后,对钟表产生了浓厚的兴趣,并展开了激烈的讨论.下列说法正确的是( )
A.小赵:“经过,时针转了.”
B.小钱:“经过,分针转了.”
C.小孙:“当时钟显示的时刻为时,时针与分针所成的锐角为.”
D.小李:“时钟的时针与分针一天内重合22次.”
11.已知角与角的终边相同,则角可以是( )
A. B. C. D.
12.与终边相同的角是( )
A. B. C. D.
三、填空题
13.把分针拨快15分钟,则分针转过的角度为________.
14.在半径为10的圆中,圆心角为240°的扇形所对的弧的长度为______.
15.已知弧长为的弧所对圆周角为,则这条弧所在圆的半径为____________.
16.桃湖公园有一扇形花园,扇形的圆心角为,半径为,现要在该花园的周围围一圈护栏,则护栏的总长度为(结果保留)_______________m.
四、解答题
17.角与角的终边相同,判断角的终边所在位置.
18.已知角的7倍角的终边与角的终边重合,且,求满足条件的角的集合
19.用弧度制分别表示每个图中顶点在原点、始边重合于x轴的非负半轴、终边落在阴影部分内(包括边界)的角的集合.
20.有相互啮合的两个齿轮,如图,大轮有48齿,小轮有20齿,当大轮转动一周时,小轮转动的角的弧度数是多少?如果大轮的转速为(即转/分),那么小轮上一点每转过的弧度数是多少?
参考答案
1.答案:A
解析:与角终边相同的角的集合表示为,当时,,故与角终边相同.故选A.
2.答案:B
解析:与 终边相同的角为,,
结合选项可知, 当式,符合题意的角为.
故选:B.
3.答案:D
解析:因为与角终边相同的角是,,所以与角终边相同的角是.故选D.
4.答案:B
解析:延长,交于点O,设圆台上 下个底面的圆心分别为,.连接,
设,,.因为,所以,
则.设所求圆心角为,则,所以.
5.答案:B
解析:由题意图1中小扇形的弧长为,大扇形的弧长为,
设扇形的圆心角为,小扇形的半径为r,则大扇形的半径为,
所以,解得,
所以原扇形纸壳中扇形的圆心角为.
故选:B.
6.答案:C
解析:对于A,,其终边与的终边相同,与的终边不相同,A错;
对于B,,其终边与的终边相同,与的终边不相同,B错;
对于C,,其终边与的终边相同,C对;
对于D,,其终边与的终边相同,与的终边不相同,D错.
故选:C
7.答案:D
解析:因为与角终边相同的角是,所以与角终边相同的角是.故选D.
8.答案:B
解析:角,与角的终边相同,
当时,
故选:B.
9.答案:BC
解析:
10.答案:ACD
解析:
A √ 经过,时针转过的角度为.
B × 经过,分针转过的角度为.
C √ 该时刻时针与分针所成的锐角为.
D √ 分针比时针多走一圈便会重合1次,一天中时针走了2圈,分针走了24圈,所以时钟的时针与分针一天内重合(次).
11.答案:BD
解析:依题意,,
当时,,
当时,,
所以BD选项符合,AC选项不符合.
故选:BD
12.答案:BC
解析:与终边相同的角为,
对A选项:,故A错误;
对B选项:,故B正确;
对C选项:,故C正确;
对D选项:,故D错误.
故选:BC.
13.答案:
解析:分针拨快15分钟,则分针转过的角度为.
故答案为:.
14.答案:
解析:.
15.答案:1
解析:已知弧长为的弧所对圆周角为,
则所对的圆心角为,
,,
故答案为:1.
16.答案:
解析:圆心角为,即,
所以扇形的弧长为,周长.
17.答案:在第二或第三象限或x轴的非负半轴上
解析:因为角与角的终边相同,所以,
所以.
当时,,此时角的终边在x轴的非负半轴上;
当时,,此时角的终边在第二象限;
当时,,此时角的终边在第三象限.
综上,角的终边在第二或第三象限或x轴的非负半轴上.
18.答案:.
解析:由题意知, ,,
即,,,,
由,得,,
,,即,2,3,4,5,
角的集合为:.
19.答案:见解析
解析:图1:;
图2:;
图3:.
20.答案:
解析:设当大轮转动一周时,小轮转动的角的弧度数是,
则,即.
如果大轮的转速为,则大轮每转,即,
记小轮每转动的角的弧度数是,则,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年高一数学苏教版必修一课时作业 7.1 角与弧度
一、选择题
1.下列选项中,与角终边相同的角是( )
A. B. C. D.
2.下列各角中与终边相同的角为( )
A. B. C. D.
3.与角终边相同的角是( )
A. B. C. D.
4.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面中,,,则原扇形纸壳中扇形的圆心角为( )
A. B. C. D.
5.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面中,,,则原扇形纸壳中扇形的圆心角为( )
A. B. C. D.
6.下列各对角中终边相同的是( )
A.和 B.和 C.和 D.和
7.与角终边相同的角是( )
A. B. C. D.
8.下列角中与终边相同的是( )
A. B. C. D.
二、多项选择题
9.已知角与的终边相同,则角可以是( )
A. B. C. D.
10.高一某班的同学在学习了任意角后,对钟表产生了浓厚的兴趣,并展开了激烈的讨论.下列说法正确的是( )
A.小赵:“经过,时针转了.”
B.小钱:“经过,分针转了.”
C.小孙:“当时钟显示的时刻为时,时针与分针所成的锐角为.”
D.小李:“时钟的时针与分针一天内重合22次.”
11.已知角与角的终边相同,则角可以是( )
A. B. C. D.
12.与终边相同的角是( )
A. B. C. D.
三、填空题
13.把分针拨快15分钟,则分针转过的角度为________.
14.在半径为10的圆中,圆心角为240°的扇形所对的弧的长度为______.
15.已知弧长为的弧所对圆周角为,则这条弧所在圆的半径为____________.
16.桃湖公园有一扇形花园,扇形的圆心角为,半径为,现要在该花园的周围围一圈护栏,则护栏的总长度为(结果保留)_______________m.
四、解答题
17.角与角的终边相同,判断角的终边所在位置.
18.已知角的7倍角的终边与角的终边重合,且,求满足条件的角的集合
19.用弧度制分别表示每个图中顶点在原点、始边重合于x轴的非负半轴、终边落在阴影部分内(包括边界)的角的集合.
20.有相互啮合的两个齿轮,如图,大轮有48齿,小轮有20齿,当大轮转动一周时,小轮转动的角的弧度数是多少?如果大轮的转速为(即转/分),那么小轮上一点每转过的弧度数是多少?
参考答案
1.答案:A
解析:与角终边相同的角的集合表示为,当时,,故与角终边相同.故选A.
2.答案:B
解析:与 终边相同的角为,,
结合选项可知, 当式,符合题意的角为.
故选:B.
3.答案:D
解析:因为与角终边相同的角是,,所以与角终边相同的角是.故选D.
4.答案:B
解析:延长,交于点O,设圆台上 下个底面的圆心分别为,.连接,
设,,.因为,所以,
则.设所求圆心角为,则,所以.
5.答案:B
解析:由题意图1中小扇形的弧长为,大扇形的弧长为,
设扇形的圆心角为,小扇形的半径为r,则大扇形的半径为,
所以,解得,
所以原扇形纸壳中扇形的圆心角为.
故选:B.
6.答案:C
解析:对于A,,其终边与的终边相同,与的终边不相同,A错;
对于B,,其终边与的终边相同,与的终边不相同,B错;
对于C,,其终边与的终边相同,C对;
对于D,,其终边与的终边相同,与的终边不相同,D错.
故选:C
7.答案:D
解析:因为与角终边相同的角是,所以与角终边相同的角是.故选D.
8.答案:B
解析:角,与角的终边相同,
当时,
故选:B.
9.答案:BC
解析:
10.答案:ACD
解析:
A √ 经过,时针转过的角度为.
B × 经过,分针转过的角度为.
C √ 该时刻时针与分针所成的锐角为.
D √ 分针比时针多走一圈便会重合1次,一天中时针走了2圈,分针走了24圈,所以时钟的时针与分针一天内重合(次).
11.答案:BD
解析:依题意,,
当时,,
当时,,
所以BD选项符合,AC选项不符合.
故选:BD
12.答案:BC
解析:与终边相同的角为,
对A选项:,故A错误;
对B选项:,故B正确;
对C选项:,故C正确;
对D选项:,故D错误.
故选:BC.
13.答案:
解析:分针拨快15分钟,则分针转过的角度为.
故答案为:.
14.答案:
解析:.
15.答案:1
解析:已知弧长为的弧所对圆周角为,
则所对的圆心角为,
,,
故答案为:1.
16.答案:
解析:圆心角为,即,
所以扇形的弧长为,周长.
17.答案:在第二或第三象限或x轴的非负半轴上
解析:因为角与角的终边相同,所以,
所以.
当时,,此时角的终边在x轴的非负半轴上;
当时,,此时角的终边在第二象限;
当时,,此时角的终边在第三象限.
综上,角的终边在第二或第三象限或x轴的非负半轴上.
18.答案:.
解析:由题意知, ,,
即,,,,
由,得,,
,,即,2,3,4,5,
角的集合为:.
19.答案:见解析
解析:图1:;
图2:;
图3:.
20.答案:
解析:设当大轮转动一周时,小轮转动的角的弧度数是,
则,即.
如果大轮的转速为,则大轮每转,即,
记小轮每转动的角的弧度数是,则,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
