2024-2025学年高一数学苏教版必修一课时作业 8.2 函数与数学模型(含解析)
文档属性
| 名称 | 2024-2025学年高一数学苏教版必修一课时作业 8.2 函数与数学模型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 11:39:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年高一数学苏教版必修一课时作业 8.2 函数与数学模型
一、选择题
1.国家新能源车电池衰减规定是在质保期内,电池的性能衰减不能超过,否则由厂家免费为车主更换电池.某品牌新能源车动力电池容量测试数据显示:电池的性能平均每年的衰减率为,该品牌设置的质保期至多为( )
(参考数据:,)
A.12年 B.13年 C.14年 D.15年
2.我国某科研机构新研制了一种治疗新冠肺炎的注射性新药,并已进入二期临床试验阶段.已知这种新药在注射停止后的血药含量c(t)(单位:mg/L)随着时间t(单位:h)的变化用指数模型描述,假定某药物的消除速率常数(单位:),刚注射这种新药后的初始血药含量,且这种新药在病人体内的血药含量不低于1000mg/L时才会对新冠肺炎起疗效,现给某新冠病人注射了这种新药,则该新药对病人有疗效的时长大约为( )(参考数据:,)
A.5.32h B.6.23h C.6.93h D.7.52h
3.大西洋鲑鱼每年都要逆流而上游回产地产卵,研究发现鲑鱼的游速(单位:)可以表示为,其中Q表示鲑鱼的耗氧量.则鲑鱼以的速度游动时的耗氧量与静止时的耗氧量的比值为( )
A.2600 B.2700 C.26 D.27
4.我们知道比较适合生活的安静环境的声强级L(噪音级)为,声强I(单位:)与声强级L(单位:)的函数关系式为(a,b为常数).某型号高铁行驶在无村庄区域的声强为,声强级为,驶进市区附近降低速度后的声强为,声强级为,若要使该高铁驶入市区时的声强级达到安静环境要求,则声强的最大值为( )
A. B. C. D.
5.近年来,“北斗”指路、“天宫”览胜、“墨子”传信、“嫦娥”问月……中国航天硕果累累,令国人备感自豪.这些航天器的发射中,都遵循“理想速度方程”:,其中是理想速度(单位:),是燃料燃烧时产生的喷气速度(单位:),M是火箭起飞时的总质量(单位:kg),是火箭自身的质量(单位:kg).小婷同学所在社团准备制作一个试验火箭,得到批准后,她们利用的某民用燃料燃烧时产生的喷气速度为,火箭自身的质量为4kg,燃料的质量为5kg,在不计空气阻力等因素影响的理想状态下发射,至燃料燃尽时,该试验火箭的理想速度大约为(,)( )
A. B. C. D.
6.由于我国与以美国为首的西方国家在科技领域内的竞争日益激烈,美国加大了对我国一些高科技公司的打压,为突破西方的技术封锁和打压,我国的一些科技企业积极实施了独立自主、自力更生的策略,在一些领域取得了骄人的成绩.我国某科技公司为突破“芯片卡脖子”问题,实现芯片制造的国产化,加大了对相关产业的研发投入.若该公司2020年全年投入芯片制造方面的研发资金为120亿元,在此基础上,计划以后每年投入的研发资金比上一年增长9%,则该公司全年投入芯片制造方面的研发资金开始超过200亿元的年份是( )参考数据:,,.
A.2023年 B.2024年 C.2025年 D.2026年
7.地震的震级与震源所释放的能量大小有关,可以用关系式表达,其中M为震级,E为地震能量.2022年11月21日云南红河发生了3.6级地震,此前11月19日该地发生了5.0级地震,则第一次5.0级地震能量大约是第二次3.6级地震能量的(参考数据:,)( )
A.110倍 B.115倍 C.120倍 D.126倍
8.锂电池在存放过程中会发生自放电现象,其电容量损失量随时间的变化规律为,其中Q(单位)为电池容量损失量,p是时间t的指数项,反映了时间趋势由反应级数决定,k是方程剩余项未知参数的组合,与温度T和电池初始荷电状态M等自放电影响因素有关.以某种品牌锂电池为研究对象,经实验采集数据进行拟合后获得,相关统计学参数,且预测值与实际值误差很小.在研究M对Q的影响时,其他参量可通过控制视为常数,电池自放电容量损失量随时间的变化规律为,经实验采集数据进行拟合后获得,相关统计学参数,且预测值与实际值误差很小.若该品牌电池初始荷电状态为,存放16天后,电容量损失量约为( )
(参考数据为:)
A.100.32 B.101.32 C.105.04 D.150.56
二、多项选择题
9.研究表明,地震时释放的能量E(单位:J)与地震里氏震级M之间的关系为,则( )
A.震级为2级的地震释放的能量为
B.释放能量为的地震震级为3级
C.9级地震释放的能量是8级地震释放的能量的10倍
D.释放能量之比为的两场地震的震级相差2级
10.如图,某湖泊蓝藻的面积y(单位:)与时间t(单位:月)的关系满足,则下列说法正确的是( )
A.蓝藻面积每个月的增长率为
B.蓝藻每个月增加的面积都相等
C.第4个月时,蓝藻面积就会超过
D.若蓝藻面积蔓延到,,所经过的时间分别是,,,则一定有
11.边际函数是经济学中的一个概念,在工程、技术、环保和经济管理等许多领域都有十分广泛的应用.函数的边际函数定义为.某公司每月最多生产75台机器,生产x台的收入函数(单位:元),其成本函数(单位:元),利润是收入与成本之差,设利润函数为(单位:元),则以下说法正确的是( )
A.取得最大值时每月产量为53台
B.边际利润函数的表达式为
C.利润函数与边际利润函数具有不同的最大值
D.边际利润函数说明随着产量的增加,每台利润与前一台利润差额在减少
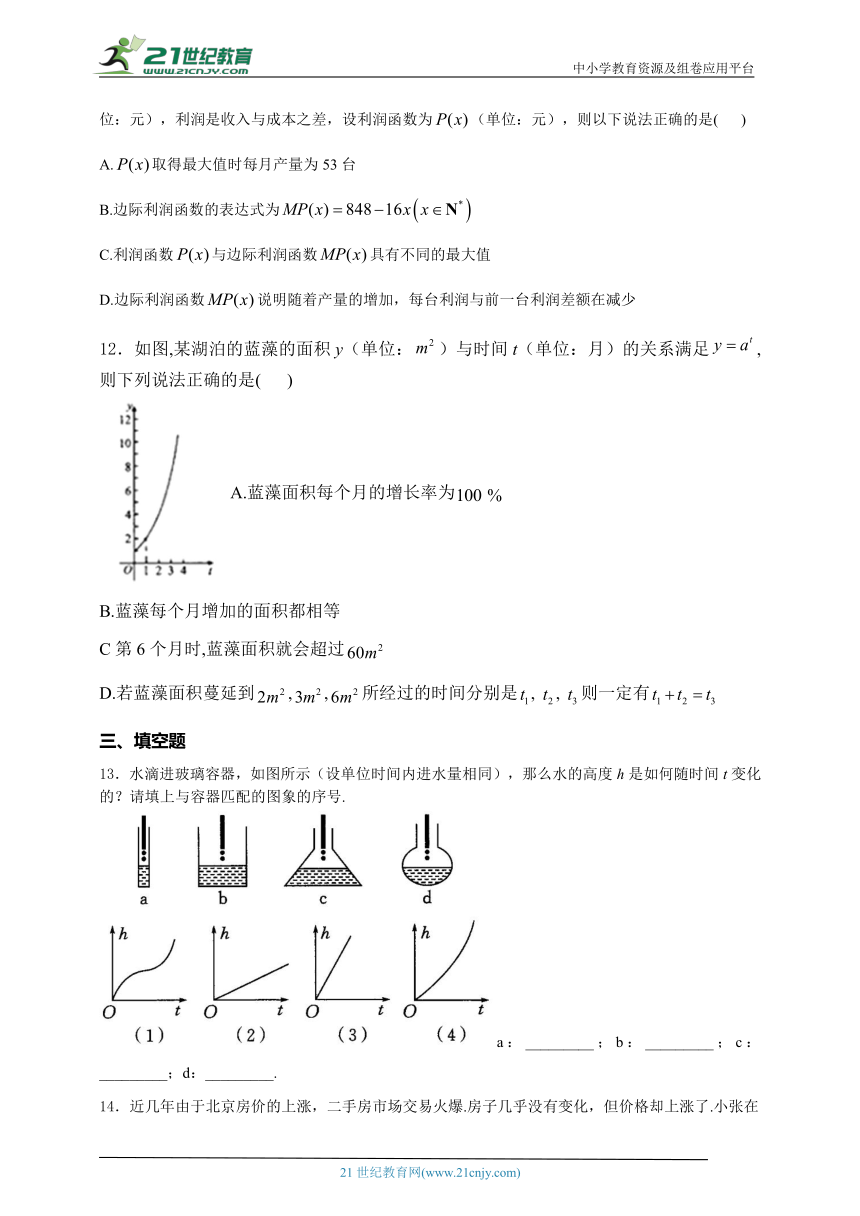
12.如图,某湖泊的蓝藻的面积y(单位:)与时间t(单位:月)的关系满足,则下列说法正确的是( )
A.蓝藻面积每个月的增长率为
B.蓝藻每个月增加的面积都相等
C第6个月时,蓝藻面积就会超过
D.若蓝藻面积蔓延到,,所经过的时间分别是,,则一定有
三、填空题
13.水滴进玻璃容器,如图所示(设单位时间内进水量相同),那么水的高度h是如何随时间t变化的?请填上与容器匹配的图象的序号.
a:_________;b:_________;c:_________;d:_________.
14.近几年由于北京房价的上涨,二手房市场交易火爆.房子几乎没有变化,但价格却上涨了.小张在2010年以80万元的价格购得一套新房,假设这10年来价格年膨胀率不变,那么到2020年,这套房子的价格y(万元)与价格年膨胀率x之间的函数关系式是__________.
15.某医用放射性物质原来的质量为a,每年衰减的百分比相同,当衰减一半时,所用的时间是10年.已知到今年为止,剩余的质量为原来的,则该放射物质已经衰减了__________年.
16.某商场以每件30元的价格购进一种商品,根据销售经验,这种商品每天的销量m(件)与售价x(元)满足一次函数,若要每天获得最大的销售利润,则每件商品的售价应定为_______________元.
四、解答题
17.已知函数和的大致图象如图所示,设这两个函数的图象相交于点和,且.
(1)请指出图中曲线,分别对应哪一个函数;
(2)若,,且,指出a,b的值,并说明理由.
18.经济学中,函数的边际函数定义为,利润函数的边际利润函数定义为.某公司最多生产100台报警系统装置,生产x台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.
(1)求利润函数的边际利润函数.
(2)利润函数与边际利润函数是否具有相等的最大值?
(3)你认为本题中边际利润函数取最大值的实际意义是什么?
19.学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分y与当天锻炼时间x(单位:分钟,)的函数关系式,要求如下:
(1)函数的图象接近图示;
(2)每天锻炼时间为0分钟时,当天得分为0分;
(3)每天锻炼时间为9分钟时,当天得分为6分;
(4)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
20.某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售单价x(单位:元/千克)满足关系式,其中,a为常数,已知销售单价为6元/千克时,每日可售出该商品220千克.
(1)求a的值;
(2)若该商品的进价为4元/千克,试确定销售单价x的值,使商场每日销售该商品所获得的利润最大,并求出利润的最大值.
参考答案
1.答案:C
解析:设该品牌设置的质保期至多为x年,
由题意可得,,则,
两边取对数,即,则,
即,则,
因为,所以,则,又因为,所以,
故选:C.
2.答案:C
解析:由题意得:,
设该药在机体内的血药浓度变为1000mg/L需要的时间为,
,
,
故,,
故该新药对病人有疗效的时长大约为.
故选:C.
3.答案:D
解析:因为鲑鱼的游速(单位:)可以表示为,其中Q表示鲑鱼的耗氧量的单位数,
当一条鲑鱼静止时,,此时,则,耗氧量为;
当一条鲑鱼以的速度游动时,,此时,
所以,则,即耗氧量为,
因此鲑鱼以1.5m/s的速度游动时的耗氧量与静止时的耗氧量的比值为.
故选:D.
4.答案:B
解析:由题意可知,解得,,所以,易得当L越大时,I越大,
所以当时,达到安静环境要求下的I取得最大值.
故选:B.
5.答案:B
解析:由于,其中,,,
所以.故选B.
6.答案:D
解析:设2020年后第n年该公司全年投入芯片制造方面的研发资金开始超过200亿元,
由得,
两边同取常用对数,得,所以,
所以从2026年开始,该公司全年投入芯片制造方面的研发资金开始超过200亿元.
故选:D.
7.答案:D
解析:第一次,即①,第二次,即②,得,即,由题可知,故.故选D.
8.答案:C
解析:根据题意,可得,,,
代入,
可得,
因为该品牌电池初始荷电状 ,
所以存放16天后,电容量损失量,
故选:C.
9.答案:BD
解析:对于A,当时,,解得,A错误;
对于B,当时,,解得,B正确;
对于C,令9级地震释放的能量为,8级地震释放的能量为,则,于是,C错误;
对于D,设释放的能量为,对应的震级为,释放的能量为,对应的震级为,
则,且,两式相减得,解得,D正确.故选BD.
10.答案:ACD
解析:由题图可知,函数的图象经过点,即,则,,不是常数.由可知蓝藻每个月的面积是上个月面积的3倍,则每个月的增长率为,A正确,B错误;
当时,,C正确;
若蓝藻面积蔓延到,,所经过的时间分别是,,,则,,,,则,D正确.故选ACD.
11.答案:BCD
解析:
A × ,二次函数的图象开口向下,对称轴为直线,因为,所以取得最大值时每月产量为53台或54台.
B √ .
C √ ,因为函数为减函数,所以.
D √ 因为函数为减函数,所以边际利润函数随着产量的增加,每台利润与前一台利润差额在减少.
12.答案:ACD
解析:由图可知,函数图象经过,
即,则, ;
不是常数,则蓝藻每个月的面积是上个月的2倍,则每个月的增长率为,A对、B错;
当时,,C对;
若蓝藻面积蔓延到,,所经过的时间分别是,,
则,,,则,即,则,D对;
故选:ACD.
13.答案:(3);(2);(4);(1)
解析:容器a和b的水面上升速度是匀速的,且容器a的水面上升得快,因此a对应(3),b对应(2),容器c的水面开始是缓慢上升,后来上升得快,而容器d的水面是开始上升得快,中间较缓慢,后来加快,因此c对应(4),d对应(1).
14.答案:
解析:这套房子一年后的价格为.
这套房子两年后的价格为,…,
由此可推得2020年,这套房子的价格y(万元)与价格年膨胀率x之间的函数关系式是.
15.答案:5
解析:设衰减的百分比为x,,由题意知,,解得,设经过m年剩余的质量为原来的,则,即,解得.
16.答案:40
解析:设某商场每天获得销售利润为y(元),
则,
因为,所以当(元)时,y取得最大值为(元).
所以若要每天获得最大的销售利润,则每件商品的售价应定为40元.
故答案为:40.
17.答案:(1)见解析
(2),;理由见解析
解析:(1)由指数函数与幂函数的增长速度知对应函数,对应函数.
(2)依题意知,是使两个函数的函数值相等的自变量x的值.当时,,即;
当时,;
当时,.
因为,,,,
所以,即;
因为,,,
,,,
,,,
所以,即.
18.答案:(1)(,)
(2)不具有相等的最大值
(3)见解析
解析:(1)由题意得
(,).
所以(,).
(2),
或63时,.
,
时,,
与不具有相等的最大值.
(3)边际利润函数当x取1时有最大值,说明生产第2台与生产第1台的总利润差最大,即第2台报警系统利润最大.
19.答案:(1)
(2)29.25
解析:(1)对于模型①:由题意,有得.
,
当时,,不合题意,
对于模型②:的增长越来越快,图像越来越“陡峭”,不合题意.
对于模型③:由题意,有得,
,
该函数图像增长符合题设图像要求.
当时,
,
符合题意,
综上所述,最合适的模型是模型③,其解析式为.
(2)由(1),令,
解得,
所以每天至少锻炼29.25分钟.
20.答案:(1)
(2)当时,函数取得最大值,且最大值等于440.
解析:(1)因为.且时,.
所以解得..
(2)由(1)可知,该商品每日的销售量.
所以商场每日销售该商品所获得的利润:
因为为二次函数,且开口向上,对称轴为.
所以,当时,函数取得最大值,且最大值等于440.
所以当销售价格定为6元/千克时,商场每日销售该商品所获得的利润最大,最大利润为440元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年高一数学苏教版必修一课时作业 8.2 函数与数学模型
一、选择题
1.国家新能源车电池衰减规定是在质保期内,电池的性能衰减不能超过,否则由厂家免费为车主更换电池.某品牌新能源车动力电池容量测试数据显示:电池的性能平均每年的衰减率为,该品牌设置的质保期至多为( )
(参考数据:,)
A.12年 B.13年 C.14年 D.15年
2.我国某科研机构新研制了一种治疗新冠肺炎的注射性新药,并已进入二期临床试验阶段.已知这种新药在注射停止后的血药含量c(t)(单位:mg/L)随着时间t(单位:h)的变化用指数模型描述,假定某药物的消除速率常数(单位:),刚注射这种新药后的初始血药含量,且这种新药在病人体内的血药含量不低于1000mg/L时才会对新冠肺炎起疗效,现给某新冠病人注射了这种新药,则该新药对病人有疗效的时长大约为( )(参考数据:,)
A.5.32h B.6.23h C.6.93h D.7.52h
3.大西洋鲑鱼每年都要逆流而上游回产地产卵,研究发现鲑鱼的游速(单位:)可以表示为,其中Q表示鲑鱼的耗氧量.则鲑鱼以的速度游动时的耗氧量与静止时的耗氧量的比值为( )
A.2600 B.2700 C.26 D.27
4.我们知道比较适合生活的安静环境的声强级L(噪音级)为,声强I(单位:)与声强级L(单位:)的函数关系式为(a,b为常数).某型号高铁行驶在无村庄区域的声强为,声强级为,驶进市区附近降低速度后的声强为,声强级为,若要使该高铁驶入市区时的声强级达到安静环境要求,则声强的最大值为( )
A. B. C. D.
5.近年来,“北斗”指路、“天宫”览胜、“墨子”传信、“嫦娥”问月……中国航天硕果累累,令国人备感自豪.这些航天器的发射中,都遵循“理想速度方程”:,其中是理想速度(单位:),是燃料燃烧时产生的喷气速度(单位:),M是火箭起飞时的总质量(单位:kg),是火箭自身的质量(单位:kg).小婷同学所在社团准备制作一个试验火箭,得到批准后,她们利用的某民用燃料燃烧时产生的喷气速度为,火箭自身的质量为4kg,燃料的质量为5kg,在不计空气阻力等因素影响的理想状态下发射,至燃料燃尽时,该试验火箭的理想速度大约为(,)( )
A. B. C. D.
6.由于我国与以美国为首的西方国家在科技领域内的竞争日益激烈,美国加大了对我国一些高科技公司的打压,为突破西方的技术封锁和打压,我国的一些科技企业积极实施了独立自主、自力更生的策略,在一些领域取得了骄人的成绩.我国某科技公司为突破“芯片卡脖子”问题,实现芯片制造的国产化,加大了对相关产业的研发投入.若该公司2020年全年投入芯片制造方面的研发资金为120亿元,在此基础上,计划以后每年投入的研发资金比上一年增长9%,则该公司全年投入芯片制造方面的研发资金开始超过200亿元的年份是( )参考数据:,,.
A.2023年 B.2024年 C.2025年 D.2026年
7.地震的震级与震源所释放的能量大小有关,可以用关系式表达,其中M为震级,E为地震能量.2022年11月21日云南红河发生了3.6级地震,此前11月19日该地发生了5.0级地震,则第一次5.0级地震能量大约是第二次3.6级地震能量的(参考数据:,)( )
A.110倍 B.115倍 C.120倍 D.126倍
8.锂电池在存放过程中会发生自放电现象,其电容量损失量随时间的变化规律为,其中Q(单位)为电池容量损失量,p是时间t的指数项,反映了时间趋势由反应级数决定,k是方程剩余项未知参数的组合,与温度T和电池初始荷电状态M等自放电影响因素有关.以某种品牌锂电池为研究对象,经实验采集数据进行拟合后获得,相关统计学参数,且预测值与实际值误差很小.在研究M对Q的影响时,其他参量可通过控制视为常数,电池自放电容量损失量随时间的变化规律为,经实验采集数据进行拟合后获得,相关统计学参数,且预测值与实际值误差很小.若该品牌电池初始荷电状态为,存放16天后,电容量损失量约为( )
(参考数据为:)
A.100.32 B.101.32 C.105.04 D.150.56
二、多项选择题
9.研究表明,地震时释放的能量E(单位:J)与地震里氏震级M之间的关系为,则( )
A.震级为2级的地震释放的能量为
B.释放能量为的地震震级为3级
C.9级地震释放的能量是8级地震释放的能量的10倍
D.释放能量之比为的两场地震的震级相差2级
10.如图,某湖泊蓝藻的面积y(单位:)与时间t(单位:月)的关系满足,则下列说法正确的是( )
A.蓝藻面积每个月的增长率为
B.蓝藻每个月增加的面积都相等
C.第4个月时,蓝藻面积就会超过
D.若蓝藻面积蔓延到,,所经过的时间分别是,,,则一定有
11.边际函数是经济学中的一个概念,在工程、技术、环保和经济管理等许多领域都有十分广泛的应用.函数的边际函数定义为.某公司每月最多生产75台机器,生产x台的收入函数(单位:元),其成本函数(单位:元),利润是收入与成本之差,设利润函数为(单位:元),则以下说法正确的是( )
A.取得最大值时每月产量为53台
B.边际利润函数的表达式为
C.利润函数与边际利润函数具有不同的最大值
D.边际利润函数说明随着产量的增加,每台利润与前一台利润差额在减少
12.如图,某湖泊的蓝藻的面积y(单位:)与时间t(单位:月)的关系满足,则下列说法正确的是( )
A.蓝藻面积每个月的增长率为
B.蓝藻每个月增加的面积都相等
C第6个月时,蓝藻面积就会超过
D.若蓝藻面积蔓延到,,所经过的时间分别是,,则一定有
三、填空题
13.水滴进玻璃容器,如图所示(设单位时间内进水量相同),那么水的高度h是如何随时间t变化的?请填上与容器匹配的图象的序号.
a:_________;b:_________;c:_________;d:_________.
14.近几年由于北京房价的上涨,二手房市场交易火爆.房子几乎没有变化,但价格却上涨了.小张在2010年以80万元的价格购得一套新房,假设这10年来价格年膨胀率不变,那么到2020年,这套房子的价格y(万元)与价格年膨胀率x之间的函数关系式是__________.
15.某医用放射性物质原来的质量为a,每年衰减的百分比相同,当衰减一半时,所用的时间是10年.已知到今年为止,剩余的质量为原来的,则该放射物质已经衰减了__________年.
16.某商场以每件30元的价格购进一种商品,根据销售经验,这种商品每天的销量m(件)与售价x(元)满足一次函数,若要每天获得最大的销售利润,则每件商品的售价应定为_______________元.
四、解答题
17.已知函数和的大致图象如图所示,设这两个函数的图象相交于点和,且.
(1)请指出图中曲线,分别对应哪一个函数;
(2)若,,且,指出a,b的值,并说明理由.
18.经济学中,函数的边际函数定义为,利润函数的边际利润函数定义为.某公司最多生产100台报警系统装置,生产x台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.
(1)求利润函数的边际利润函数.
(2)利润函数与边际利润函数是否具有相等的最大值?
(3)你认为本题中边际利润函数取最大值的实际意义是什么?
19.学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分y与当天锻炼时间x(单位:分钟,)的函数关系式,要求如下:
(1)函数的图象接近图示;
(2)每天锻炼时间为0分钟时,当天得分为0分;
(3)每天锻炼时间为9分钟时,当天得分为6分;
(4)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
20.某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售单价x(单位:元/千克)满足关系式,其中,a为常数,已知销售单价为6元/千克时,每日可售出该商品220千克.
(1)求a的值;
(2)若该商品的进价为4元/千克,试确定销售单价x的值,使商场每日销售该商品所获得的利润最大,并求出利润的最大值.
参考答案
1.答案:C
解析:设该品牌设置的质保期至多为x年,
由题意可得,,则,
两边取对数,即,则,
即,则,
因为,所以,则,又因为,所以,
故选:C.
2.答案:C
解析:由题意得:,
设该药在机体内的血药浓度变为1000mg/L需要的时间为,
,
,
故,,
故该新药对病人有疗效的时长大约为.
故选:C.
3.答案:D
解析:因为鲑鱼的游速(单位:)可以表示为,其中Q表示鲑鱼的耗氧量的单位数,
当一条鲑鱼静止时,,此时,则,耗氧量为;
当一条鲑鱼以的速度游动时,,此时,
所以,则,即耗氧量为,
因此鲑鱼以1.5m/s的速度游动时的耗氧量与静止时的耗氧量的比值为.
故选:D.
4.答案:B
解析:由题意可知,解得,,所以,易得当L越大时,I越大,
所以当时,达到安静环境要求下的I取得最大值.
故选:B.
5.答案:B
解析:由于,其中,,,
所以.故选B.
6.答案:D
解析:设2020年后第n年该公司全年投入芯片制造方面的研发资金开始超过200亿元,
由得,
两边同取常用对数,得,所以,
所以从2026年开始,该公司全年投入芯片制造方面的研发资金开始超过200亿元.
故选:D.
7.答案:D
解析:第一次,即①,第二次,即②,得,即,由题可知,故.故选D.
8.答案:C
解析:根据题意,可得,,,
代入,
可得,
因为该品牌电池初始荷电状 ,
所以存放16天后,电容量损失量,
故选:C.
9.答案:BD
解析:对于A,当时,,解得,A错误;
对于B,当时,,解得,B正确;
对于C,令9级地震释放的能量为,8级地震释放的能量为,则,于是,C错误;
对于D,设释放的能量为,对应的震级为,释放的能量为,对应的震级为,
则,且,两式相减得,解得,D正确.故选BD.
10.答案:ACD
解析:由题图可知,函数的图象经过点,即,则,,不是常数.由可知蓝藻每个月的面积是上个月面积的3倍,则每个月的增长率为,A正确,B错误;
当时,,C正确;
若蓝藻面积蔓延到,,所经过的时间分别是,,,则,,,,则,D正确.故选ACD.
11.答案:BCD
解析:
A × ,二次函数的图象开口向下,对称轴为直线,因为,所以取得最大值时每月产量为53台或54台.
B √ .
C √ ,因为函数为减函数,所以.
D √ 因为函数为减函数,所以边际利润函数随着产量的增加,每台利润与前一台利润差额在减少.
12.答案:ACD
解析:由图可知,函数图象经过,
即,则, ;
不是常数,则蓝藻每个月的面积是上个月的2倍,则每个月的增长率为,A对、B错;
当时,,C对;
若蓝藻面积蔓延到,,所经过的时间分别是,,
则,,,则,即,则,D对;
故选:ACD.
13.答案:(3);(2);(4);(1)
解析:容器a和b的水面上升速度是匀速的,且容器a的水面上升得快,因此a对应(3),b对应(2),容器c的水面开始是缓慢上升,后来上升得快,而容器d的水面是开始上升得快,中间较缓慢,后来加快,因此c对应(4),d对应(1).
14.答案:
解析:这套房子一年后的价格为.
这套房子两年后的价格为,…,
由此可推得2020年,这套房子的价格y(万元)与价格年膨胀率x之间的函数关系式是.
15.答案:5
解析:设衰减的百分比为x,,由题意知,,解得,设经过m年剩余的质量为原来的,则,即,解得.
16.答案:40
解析:设某商场每天获得销售利润为y(元),
则,
因为,所以当(元)时,y取得最大值为(元).
所以若要每天获得最大的销售利润,则每件商品的售价应定为40元.
故答案为:40.
17.答案:(1)见解析
(2),;理由见解析
解析:(1)由指数函数与幂函数的增长速度知对应函数,对应函数.
(2)依题意知,是使两个函数的函数值相等的自变量x的值.当时,,即;
当时,;
当时,.
因为,,,,
所以,即;
因为,,,
,,,
,,,
所以,即.
18.答案:(1)(,)
(2)不具有相等的最大值
(3)见解析
解析:(1)由题意得
(,).
所以(,).
(2),
或63时,.
,
时,,
与不具有相等的最大值.
(3)边际利润函数当x取1时有最大值,说明生产第2台与生产第1台的总利润差最大,即第2台报警系统利润最大.
19.答案:(1)
(2)29.25
解析:(1)对于模型①:由题意,有得.
,
当时,,不合题意,
对于模型②:的增长越来越快,图像越来越“陡峭”,不合题意.
对于模型③:由题意,有得,
,
该函数图像增长符合题设图像要求.
当时,
,
符合题意,
综上所述,最合适的模型是模型③,其解析式为.
(2)由(1),令,
解得,
所以每天至少锻炼29.25分钟.
20.答案:(1)
(2)当时,函数取得最大值,且最大值等于440.
解析:(1)因为.且时,.
所以解得..
(2)由(1)可知,该商品每日的销售量.
所以商场每日销售该商品所获得的利润:
因为为二次函数,且开口向上,对称轴为.
所以,当时,函数取得最大值,且最大值等于440.
所以当销售价格定为6元/千克时,商场每日销售该商品所获得的利润最大,最大利润为440元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
