青岛版(六三制)数学八年级上册 5.5直角三角形全等的判定课件(共17张PPT)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 5.5直角三角形全等的判定课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 493.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 08:11:10 | ||
图片预览




文档简介
(共17张PPT)
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就可以全等了呢?
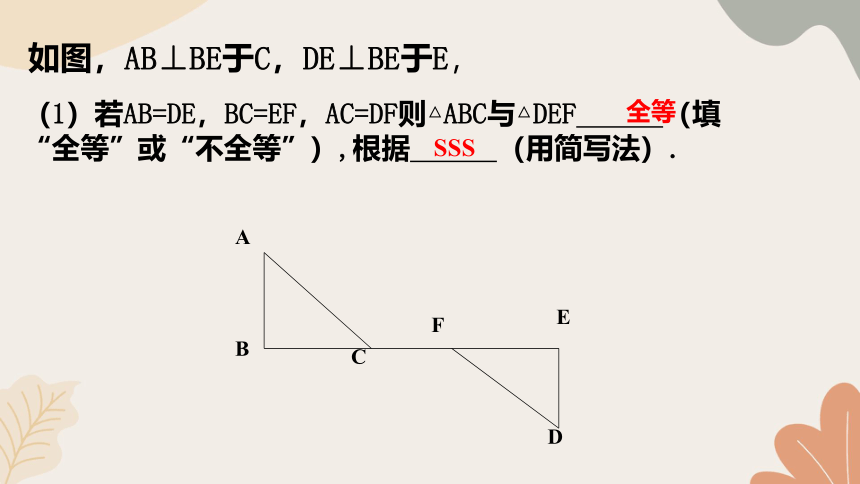
如图,AB⊥BE于C,DE⊥BE于E,
A
B
C
D
E
F
(1)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等”),根据 (用简写法).
全等
SSS
A
B
C
D
E
F
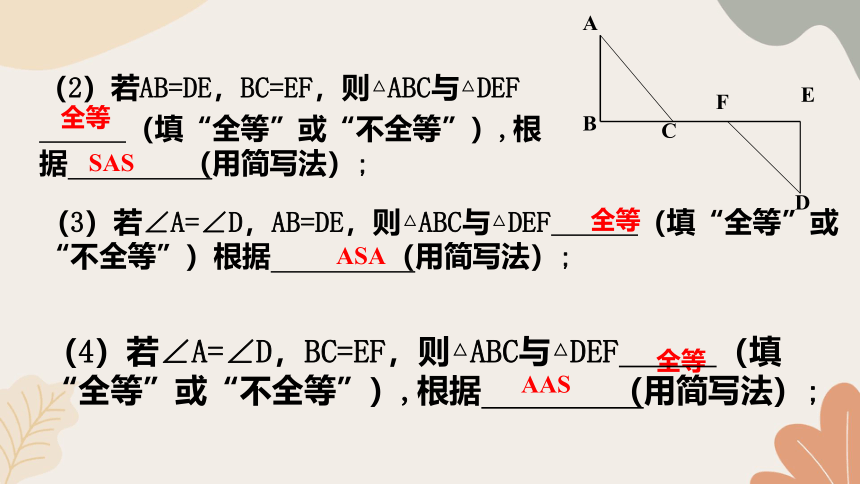
(2)若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”),根据 (用简写法);
AAS
全等
(3)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法);
全等
SAS
(4)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等”),根据 (用简写法);
全等
ASA
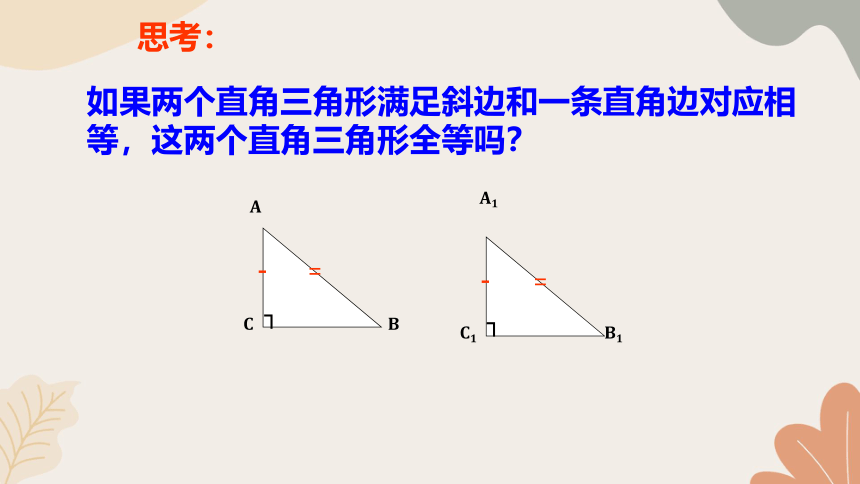
思考:
A
B
C
A1
B1
C1
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
┐
┐
-
-
=
=
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
1.理解用“HL”的方法判定直角三角形全等.
2.会熟练运用“HL”证明直角三角形的全等,并解决一些简单问题.
3.经历探究直角三角形全等条件的过程,体会一般与特殊的辨证关系.
自学目标:
自学提示:根据我们的自学方法自学课本41页~42页的内容。
SSS
SAS
ASA
AAS
斜边
一直角边
自学交流展示:
做 一 做
任意画出一个Rt△ABC,使∠C=90, 再画一个Rt△A B C ,使∠C =90o,B C =BC,A B =AB.
它们全等吗
A
B
C
A
B
C
即斜边和一条直角边对应相等
AB = DE
AC= DF
在Rt△ABC与Rt△DEF中,
Rt △ABC ≌ Rt △ DEF(HL)
A
B
C
D
E
F
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
记一记
练一练
1、如图1:在△ABC中,AB=AC, AD垂直BC,
则△ABD △ACD。
A
B
D
C
C
D
B
A
≌
练一练
若根据“HL”判定,还需要加条件:
, ;
或: , 。
AD = BD
BE=AC
2、如图: AD垂直BC,E在AD上,要使△ADC ≌△BDE。
C
D
B
A
E
BE=AC
DE=DC
70°
HL
交流展示:
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
学以致用
先把它转化为一个纯数学问题:
已知:如图,AC=DF,AC⊥AB,DE⊥DF.
求证:∠ABC=∠DFE.
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
思维拓展
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
思维拓展
小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
1、书44页习题12.2第7、8题
2、能力练习册29页1-9题
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就可以全等了呢?
如图,AB⊥BE于C,DE⊥BE于E,
A
B
C
D
E
F
(1)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等”),根据 (用简写法).
全等
SSS
A
B
C
D
E
F
(2)若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”),根据 (用简写法);
AAS
全等
(3)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法);
全等
SAS
(4)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等”),根据 (用简写法);
全等
ASA
思考:
A
B
C
A1
B1
C1
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
┐
┐
-
-
=
=
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
1.理解用“HL”的方法判定直角三角形全等.
2.会熟练运用“HL”证明直角三角形的全等,并解决一些简单问题.
3.经历探究直角三角形全等条件的过程,体会一般与特殊的辨证关系.
自学目标:
自学提示:根据我们的自学方法自学课本41页~42页的内容。
SSS
SAS
ASA
AAS
斜边
一直角边
自学交流展示:
做 一 做
任意画出一个Rt△ABC,使∠C=90, 再画一个Rt△A B C ,使∠C =90o,B C =BC,A B =AB.
它们全等吗
A
B
C
A
B
C
即斜边和一条直角边对应相等
AB = DE
AC= DF
在Rt△ABC与Rt△DEF中,
Rt △ABC ≌ Rt △ DEF(HL)
A
B
C
D
E
F
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
记一记
练一练
1、如图1:在△ABC中,AB=AC, AD垂直BC,
则△ABD △ACD。
A
B
D
C
C
D
B
A
≌
练一练
若根据“HL”判定,还需要加条件:
, ;
或: , 。
AD = BD
BE=AC
2、如图: AD垂直BC,E在AD上,要使△ADC ≌△BDE。
C
D
B
A
E
BE=AC
DE=DC
70°
HL
交流展示:
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
学以致用
先把它转化为一个纯数学问题:
已知:如图,AC=DF,AC⊥AB,DE⊥DF.
求证:∠ABC=∠DFE.
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
思维拓展
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
思维拓展
小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
1、书44页习题12.2第7、8题
2、能力练习册29页1-9题
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
