(8)二次函数y=ax2的图象和性质—九年级数学人教版上册课前导学(含解析)
文档属性
| 名称 | (8)二次函数y=ax2的图象和性质—九年级数学人教版上册课前导学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 222.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 22:12:42 | ||
图片预览

文档简介
(8)二次函数y = ax2的图象和性质(第一课时)—九年级数学人教版上册课前导学
一、知识预习
1.抛物线的图象性质:
(1)抛物线的对称轴是 ,顶点是 ;
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最 点,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
(3)当a<0时,抛物线的开口向下,顶点是抛物线的最 点,当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
(4)|a|越大,抛物线的开口越 .
二、自我检测
1.二次函数的图象经过,则a的值为( )
A. B. C.1 D.2
2.已知二次函数,当时,y随x的增大而增大,则实数a的取值范围是( )
A. B. C. D.
3.下列关于函数的叙述中,错误的是( )
A.y有最大值
B.图像的对称轴是y轴
C.当时,y随x的增大而增大
D.图像的顶点是原点
4.已知,则下列说法错误的是( )
A.函数图象开口向下
B.函数图象的对称轴是y轴
C.当时,y随x的增大而减小
D.函数有最小值
5.在同一平面直角坐标系中,画函数,,的图象,它们图象的共同特点是( )
A.都是关于y轴对称,抛物线开口向上
B.都是关于y轴对称,抛物线的顶点都是原点
C.当时,y随x的增大而增大
D.抛物线的顶点都是原点,顶点是抛物线的最低点
6.已知抛物线过,两点,则,与0的大小关系是_________.
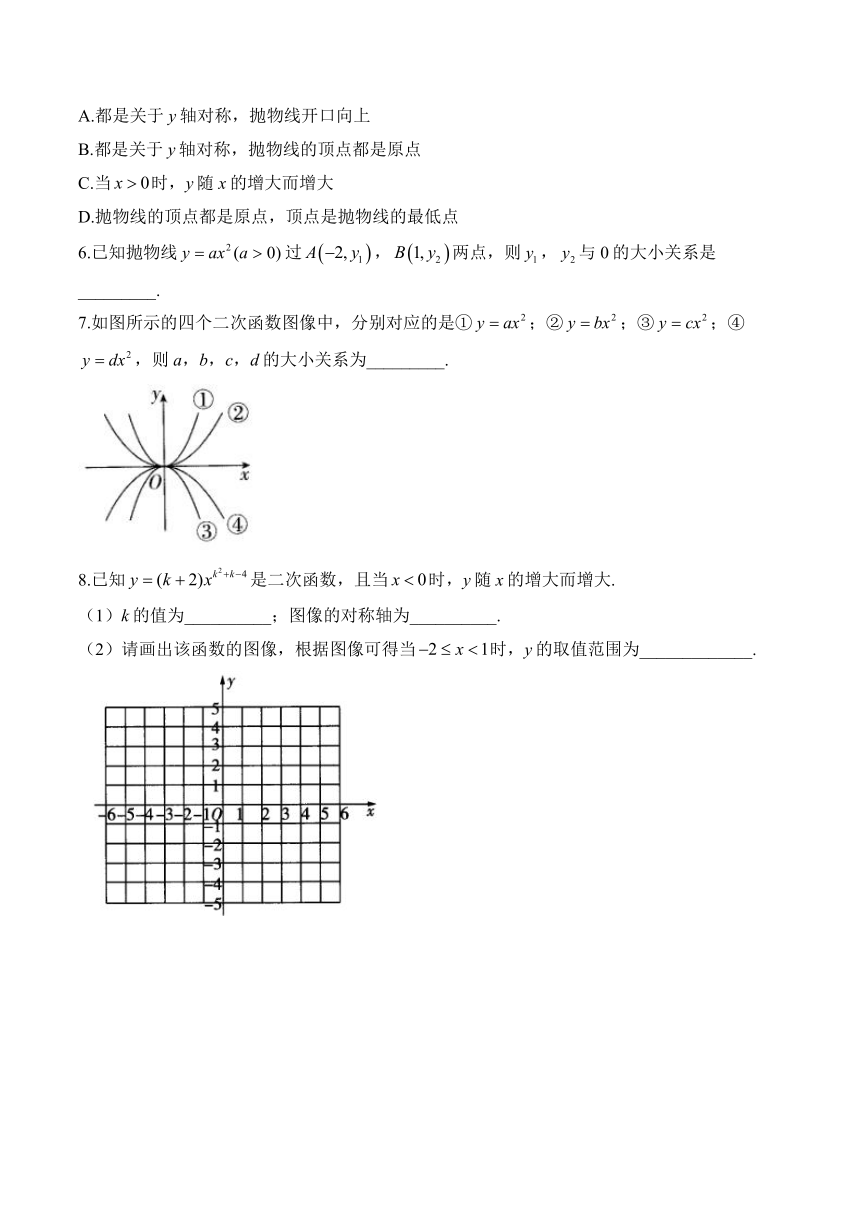
7.如图所示的四个二次函数图像中,分别对应的是①;②;③;④,则a,b,c,d的大小关系为_________.
8.已知是二次函数,且当时,y随x的增大而增大.
(1)k的值为__________;图像的对称轴为__________.
(2)请画出该函数的图像,根据图像可得当时,y的取值范围为_____________.
答案以及解析
一、知识预习
1. y轴 原点 低 高 小
二、自我检测
1.答案:D
解析:将代入,得:;
故选:D.
2.答案:B
解析:由题意可知,,所以.
3.答案:A
解析:函数的图像开口向上,顶点是原点,对称轴是y轴,当时,y随x的增大而增大,y有最小值,故A错误,B,C,D正确.
4.答案:D
解析:易知的图象开口向下,对称轴是y轴,当时,y随x的增大而减小,函数有最大值.
5.答案:B
解析:在同一平面直角坐标系中,画函数,,的图象,如图,
A、三个函数的图象都是关于y轴对称,函数和的图象开口向上,函数的图象开口向下,故此选项说法错误,不符合题意;
B、三个函数的图象都是关于y轴对称,抛物线的顶点都是原点,故此选项说法正确,符合题意;
C、函数和,当时,y随x的增大而增大;函数,当时,y随x的增大而减小,故此选项说法错误,不符合题意;
D、三个函数的图象的顶点都是原点,函数和的图象的顶点是最低点,函数的图象的顶点是最高点,故此选项说法错误,不符合题意;
故选:B.
6.答案:
解析:关于y轴对称的点的坐标为,且,,.故答案为.
7.答案:
解析:如图,作直线,则与四条抛物线的交点从上到下依次为,,,,.
8.答案:(1);y轴(或直线)
(2)
解析:(1)由是二次函数,
且当时,y随x的增大而增大,
得,,
二次函数的表达式为,
图像的对称轴为y轴(或直线).
(2)函数图像如图所示:
若,则根据函数图像可知,当时,y取得最大值0,当时,y取得最小值-4,当时,.
一、知识预习
1.抛物线的图象性质:
(1)抛物线的对称轴是 ,顶点是 ;
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最 点,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
(3)当a<0时,抛物线的开口向下,顶点是抛物线的最 点,当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
(4)|a|越大,抛物线的开口越 .
二、自我检测
1.二次函数的图象经过,则a的值为( )
A. B. C.1 D.2
2.已知二次函数,当时,y随x的增大而增大,则实数a的取值范围是( )
A. B. C. D.
3.下列关于函数的叙述中,错误的是( )
A.y有最大值
B.图像的对称轴是y轴
C.当时,y随x的增大而增大
D.图像的顶点是原点
4.已知,则下列说法错误的是( )
A.函数图象开口向下
B.函数图象的对称轴是y轴
C.当时,y随x的增大而减小
D.函数有最小值
5.在同一平面直角坐标系中,画函数,,的图象,它们图象的共同特点是( )
A.都是关于y轴对称,抛物线开口向上
B.都是关于y轴对称,抛物线的顶点都是原点
C.当时,y随x的增大而增大
D.抛物线的顶点都是原点,顶点是抛物线的最低点
6.已知抛物线过,两点,则,与0的大小关系是_________.
7.如图所示的四个二次函数图像中,分别对应的是①;②;③;④,则a,b,c,d的大小关系为_________.
8.已知是二次函数,且当时,y随x的增大而增大.
(1)k的值为__________;图像的对称轴为__________.
(2)请画出该函数的图像,根据图像可得当时,y的取值范围为_____________.
答案以及解析
一、知识预习
1. y轴 原点 低 高 小
二、自我检测
1.答案:D
解析:将代入,得:;
故选:D.
2.答案:B
解析:由题意可知,,所以.
3.答案:A
解析:函数的图像开口向上,顶点是原点,对称轴是y轴,当时,y随x的增大而增大,y有最小值,故A错误,B,C,D正确.
4.答案:D
解析:易知的图象开口向下,对称轴是y轴,当时,y随x的增大而减小,函数有最大值.
5.答案:B
解析:在同一平面直角坐标系中,画函数,,的图象,如图,
A、三个函数的图象都是关于y轴对称,函数和的图象开口向上,函数的图象开口向下,故此选项说法错误,不符合题意;
B、三个函数的图象都是关于y轴对称,抛物线的顶点都是原点,故此选项说法正确,符合题意;
C、函数和,当时,y随x的增大而增大;函数,当时,y随x的增大而减小,故此选项说法错误,不符合题意;
D、三个函数的图象的顶点都是原点,函数和的图象的顶点是最低点,函数的图象的顶点是最高点,故此选项说法错误,不符合题意;
故选:B.
6.答案:
解析:关于y轴对称的点的坐标为,且,,.故答案为.
7.答案:
解析:如图,作直线,则与四条抛物线的交点从上到下依次为,,,,.
8.答案:(1);y轴(或直线)
(2)
解析:(1)由是二次函数,
且当时,y随x的增大而增大,
得,,
二次函数的表达式为,
图像的对称轴为y轴(或直线).
(2)函数图像如图所示:
若,则根据函数图像可知,当时,y取得最大值0,当时,y取得最小值-4,当时,.
同课章节目录
