(6)实际问题与一元二次方程—九年级数学人教版上册课前导学(含解析)
文档属性
| 名称 | (6)实际问题与一元二次方程—九年级数学人教版上册课前导学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 101.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 22:13:43 | ||
图片预览

文档简介
(6)实际问题与一元二次方程—九年级数学人教版上册课前导学
一、知识预习
列一元二次方程解用用题的一般步骤:
(1)审题,明确已知和未知;
(2)找相等关系,设未知数;
(3) ;
(4) ;
(5)检验根的合理性;
(6)作答.
二、自我检测
1.有1人患了流感后,经过两轮传染后共有144人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了x人,则根据题意可列方程( )
A. B. C. D.
2.某品牌手机原来每部售价为元,经过连续两次降价后,该手机每部售价为元,设平均每次降价的百分率为x,根据题意,所列方程正确的是( )
A. B.
C. D.
3.为大力实施城市绿化行动,某小区规划设置一片面积为1000平方米的矩形绿地,并且长比宽多30米,设绿地长为x米,根据题意可列方程为( )
A. B.
C. D.
4.某校要组织一场篮球联赛,每两队之间都赛2场(双循环),计划安排30场比赛,设有x支球队,可列方程为( )
A. B.
C. D.
5.2011广州大运会的某纪念品原价100元,连续两次降价后售价为81元,a的值是( )
A. B. C. D.
6.淄博烧烤风靡全国.某烧烤店今年5月份盈利20万元,预计7月份盈利28.8万元,设每月盈利增长的百分率相同,则6月份盈利___________万元.
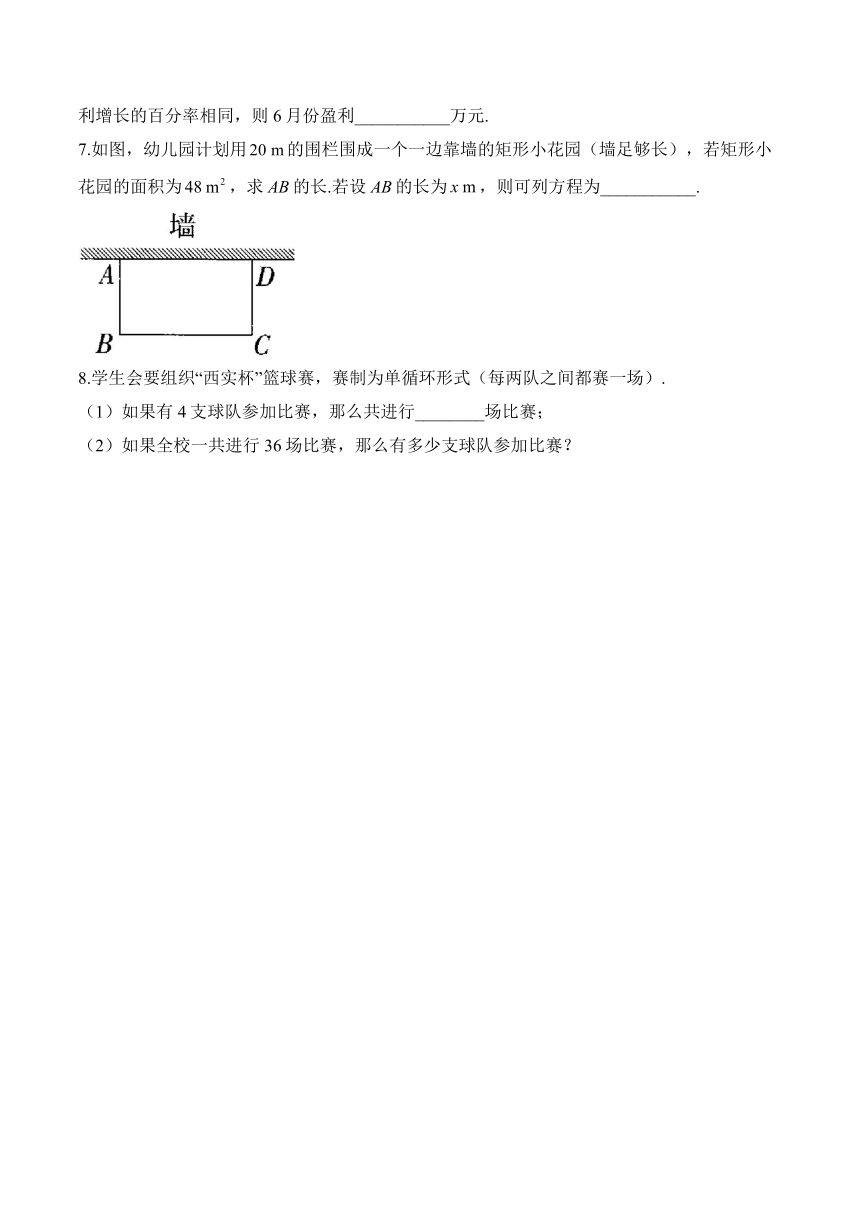
7.如图,幼儿园计划用的围栏围成一个一边靠墙的矩形小花园(墙足够长),若矩形小花园的面积为,求AB的长.若设AB的长为,则可列方程为___________.
8.学生会要组织“西实杯”篮球赛,赛制为单循环形式(每两队之间都赛一场).
(1)如果有4支球队参加比赛,那么共进行________场比赛;
(2)如果全校一共进行36场比赛,那么有多少支球队参加比赛?
答案以及解析
一、知识预习
1. 列方程 解方程
二、自我检测
1.答案:A
解析:设每轮传染中平均一个人传染了x人,则根据题意可列方程,
故选:A.
2.答案:C
解析:设平均每次降价的百分率为x,
根据题意得,
,
故选:C.
3.答案:B
解析:设绿地长为x米,则宽为米,根据题意得:
,故B正确.
故选:B.
4.答案:B
解析:设有x支球队,每两队之间都赛2场(双循环),计划安排30场比赛,
∴
故选:B.
5.答案:B
解析:根据题意列方程得
,
解得,(不符合题意,舍去)
这两次降价,即.
故选:B.
6.答案:24
解析:设每月盈利增长的百分率为x,
根据题意,得,
解得,(不合题意,舍去),
月份盈利万元.
7.答案:
解析:的长为,的长为,根据矩形的面积公式结合矩形小花园的面积为,可列方程为.
8.答案:(1)6
(2)9支
解析:(1)(场),
答:共进行6场比赛;
(2)设有x支球队参加比赛,根据题意得:
,
解得:,(不合题意,舍去).
答:有9支球队参加比赛.
一、知识预习
列一元二次方程解用用题的一般步骤:
(1)审题,明确已知和未知;
(2)找相等关系,设未知数;
(3) ;
(4) ;
(5)检验根的合理性;
(6)作答.
二、自我检测
1.有1人患了流感后,经过两轮传染后共有144人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了x人,则根据题意可列方程( )
A. B. C. D.
2.某品牌手机原来每部售价为元,经过连续两次降价后,该手机每部售价为元,设平均每次降价的百分率为x,根据题意,所列方程正确的是( )
A. B.
C. D.
3.为大力实施城市绿化行动,某小区规划设置一片面积为1000平方米的矩形绿地,并且长比宽多30米,设绿地长为x米,根据题意可列方程为( )
A. B.
C. D.
4.某校要组织一场篮球联赛,每两队之间都赛2场(双循环),计划安排30场比赛,设有x支球队,可列方程为( )
A. B.
C. D.
5.2011广州大运会的某纪念品原价100元,连续两次降价后售价为81元,a的值是( )
A. B. C. D.
6.淄博烧烤风靡全国.某烧烤店今年5月份盈利20万元,预计7月份盈利28.8万元,设每月盈利增长的百分率相同,则6月份盈利___________万元.
7.如图,幼儿园计划用的围栏围成一个一边靠墙的矩形小花园(墙足够长),若矩形小花园的面积为,求AB的长.若设AB的长为,则可列方程为___________.
8.学生会要组织“西实杯”篮球赛,赛制为单循环形式(每两队之间都赛一场).
(1)如果有4支球队参加比赛,那么共进行________场比赛;
(2)如果全校一共进行36场比赛,那么有多少支球队参加比赛?
答案以及解析
一、知识预习
1. 列方程 解方程
二、自我检测
1.答案:A
解析:设每轮传染中平均一个人传染了x人,则根据题意可列方程,
故选:A.
2.答案:C
解析:设平均每次降价的百分率为x,
根据题意得,
,
故选:C.
3.答案:B
解析:设绿地长为x米,则宽为米,根据题意得:
,故B正确.
故选:B.
4.答案:B
解析:设有x支球队,每两队之间都赛2场(双循环),计划安排30场比赛,
∴
故选:B.
5.答案:B
解析:根据题意列方程得
,
解得,(不符合题意,舍去)
这两次降价,即.
故选:B.
6.答案:24
解析:设每月盈利增长的百分率为x,
根据题意,得,
解得,(不合题意,舍去),
月份盈利万元.
7.答案:
解析:的长为,的长为,根据矩形的面积公式结合矩形小花园的面积为,可列方程为.
8.答案:(1)6
(2)9支
解析:(1)(场),
答:共进行6场比赛;
(2)设有x支球队参加比赛,根据题意得:
,
解得:,(不合题意,舍去).
答:有9支球队参加比赛.
同课章节目录
