第三章 二次函数 4 二次函数的图象与性质 第1课时 二次函数的图象与性质(含答案)
文档属性
| 名称 | 第三章 二次函数 4 二次函数的图象与性质 第1课时 二次函数的图象与性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
4 二次函数的图象与性质
第1课时 二次函数的图象与性质
1.二次函数 的顶点坐标是 ( )
2.抛物线 的对称轴是 ( )
A.直线 B.直线 C. y轴 D.直线
3.已知点 均在抛物线 上,下列说法正确的是( )
A.若 则 B.若 则
C.若 则 D.若 则
4.已知点( y ),(2,y )都在函数 的图象上,则的大小关系为 ( )
5.函数和 (为常数,且,在同一平面直角坐标系中的大致图象可能是 ( )
6.将抛物线 向下平移2个单位,平移后抛物线的表达式为______________.
7.抛物线 向上平移2个单位后所得的抛物线表达式是________________.
8.(1)将二次函数 的图象向下平移3个单位,就得到二次函数______________的图象,其顶点坐标为___________;
(2)抛物线 的开口_________,对称轴为_______,顶点坐标为__________.
9.二次函数 的最小值是____________.
10.二次函数 的最大值是____________.
11.在同一直角坐标系中,画出 和 的图象,并根据图象回答下列问题.
… -3 -2 -1 0 1 2 3 …
… …
… …
(1)抛物线 向______平移______个单位得到抛物线
(2)抛物线 开口方向是_______,对称轴为________,顶点坐标为___________;
(3)对抛物线 当x__________时,函数 y随x的增大而减小;当x___________时,函数y有最_______值,其最_______值是___________.
12.画出二次函数 的图象,根据图象回答下列问题:
(1)写出抛物线的顶点坐标和对称轴;
(2)当x取何值时,y的值随x值的增大而增大;
(3)当x取何值时,函数有最大(小)值,最大(小)值为多少
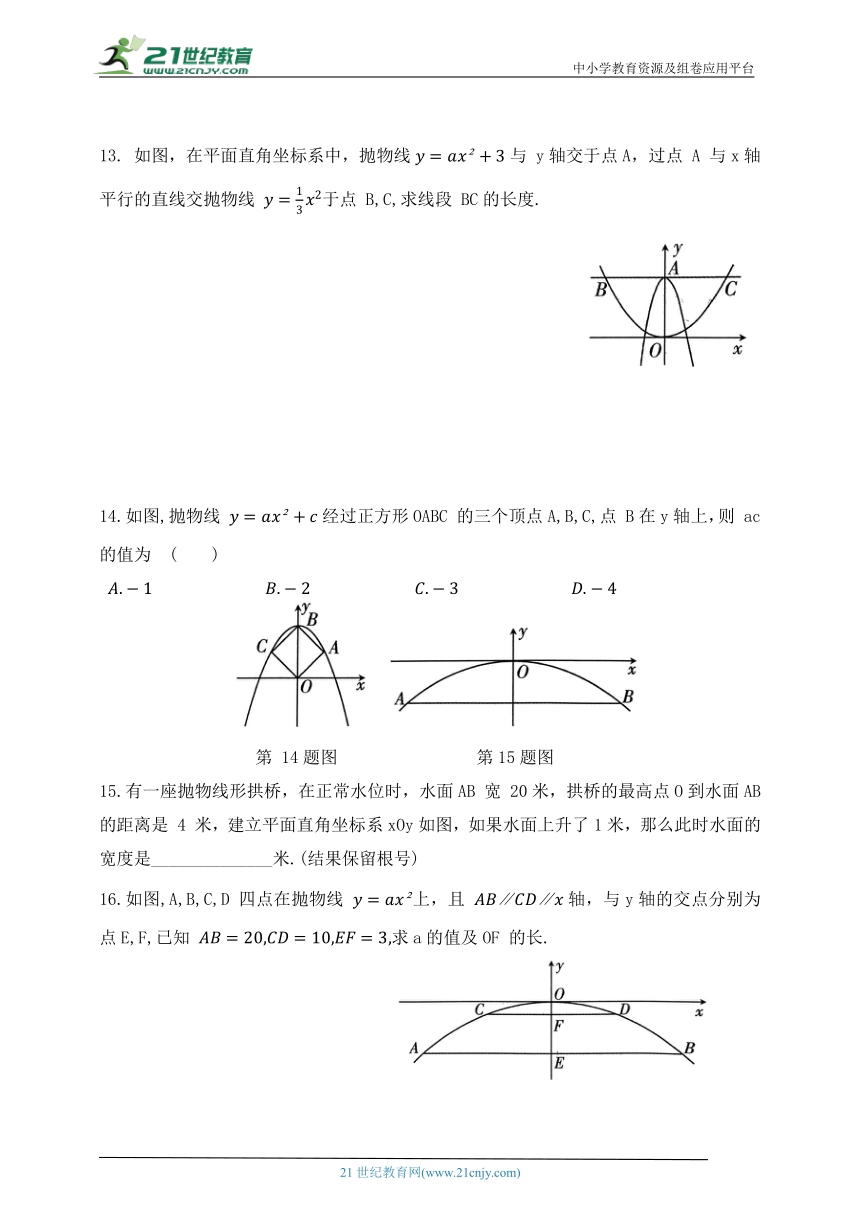
13. 如图,在平面直角坐标系中,抛物线与 y轴交于点A,过点 A 与x轴平行的直线交抛物线 于点 B,C,求线段 BC的长度.
14.如图,抛物线 经过正方形OABC 的三个顶点A,B,C,点 B在y轴上,则 ac的值为 ( )
第 14题图 第15题图
15.有一座抛物线形拱桥,在正常水位时,水面AB 宽 20米,拱桥的最高点O到水面AB 的距离是 4 米,建立平面直角坐标系xOy如图,如果水面上升了1米,那么此时水面的宽度是______________米.(结果保留根号)
16.如图,A,B,C,D 四点在抛物线 上,且 ∥∥轴,与y轴的交点分别为点E,F,已知 求a的值及OF 的长.
参考答案
1. A 2. C 3. D 4. C 5. C
(2)向下 y轴 (0,2) 9.-1 10.-6
11.解:列表如表:
… -3 -2 -1 0 1 2 3 …
… -9 -4 -1 0 -1 -4 -9 …
… -8 -3 0 1 0 -3 -8 …
描点:表中的数据作为点的坐标在平面直角坐标系中描出,
连线:用平滑的线连接,如图所示:
(1)抛物线 向下平移1个单位得到抛物线
故答案为:下,1;
(2)抛物线 的图象开口向下,对称轴为 y轴,顶点坐标为(0,1).
故答案为:向下,y轴,(0,1);
(3)对抛物线 当 时,函数 y随x 的增大而减小;当 时,函数 y有最大值,其最大值是1.
故答案为:,大,大,1.
12.解:如图所示:
(1)抛物线的顶点坐标为(0,1),对称轴为y轴;
(2)当x<0时,y的值随x值的增大而增大;
(3)当x=0时,函数有最大值,最大值为1.
13.解:当x=0时, 则 A 点坐标为(0,3).
∥轴,∴B点,C点的纵坐标都为3.
当 时, 解得 ∴B(-3,3),C(3,3),
14. B 解析:过点 A 作. 轴于点 H,
∵四边形ABCO是正方形, ∴
设A(m,m),则 B(0,2m),
解得
∴ac的值为
解析:设抛物线的表达式为
∵O点到水面AB 的距离为 4 米,∴A,B点的纵坐标为
∵水面AB宽为20米,
将 A代入 得
∵水位上升1米,∴O点到水面的距离为 3,
把y=-3代入 得
∴水面的宽度为 米.
16.解:由题意可设点 ,
则 解得
∥轴,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
4 二次函数的图象与性质
第1课时 二次函数的图象与性质
1.二次函数 的顶点坐标是 ( )
2.抛物线 的对称轴是 ( )
A.直线 B.直线 C. y轴 D.直线
3.已知点 均在抛物线 上,下列说法正确的是( )
A.若 则 B.若 则
C.若 则 D.若 则
4.已知点( y ),(2,y )都在函数 的图象上,则的大小关系为 ( )
5.函数和 (为常数,且,在同一平面直角坐标系中的大致图象可能是 ( )
6.将抛物线 向下平移2个单位,平移后抛物线的表达式为______________.
7.抛物线 向上平移2个单位后所得的抛物线表达式是________________.
8.(1)将二次函数 的图象向下平移3个单位,就得到二次函数______________的图象,其顶点坐标为___________;
(2)抛物线 的开口_________,对称轴为_______,顶点坐标为__________.
9.二次函数 的最小值是____________.
10.二次函数 的最大值是____________.
11.在同一直角坐标系中,画出 和 的图象,并根据图象回答下列问题.
… -3 -2 -1 0 1 2 3 …
… …
… …
(1)抛物线 向______平移______个单位得到抛物线
(2)抛物线 开口方向是_______,对称轴为________,顶点坐标为___________;
(3)对抛物线 当x__________时,函数 y随x的增大而减小;当x___________时,函数y有最_______值,其最_______值是___________.
12.画出二次函数 的图象,根据图象回答下列问题:
(1)写出抛物线的顶点坐标和对称轴;
(2)当x取何值时,y的值随x值的增大而增大;
(3)当x取何值时,函数有最大(小)值,最大(小)值为多少
13. 如图,在平面直角坐标系中,抛物线与 y轴交于点A,过点 A 与x轴平行的直线交抛物线 于点 B,C,求线段 BC的长度.
14.如图,抛物线 经过正方形OABC 的三个顶点A,B,C,点 B在y轴上,则 ac的值为 ( )
第 14题图 第15题图
15.有一座抛物线形拱桥,在正常水位时,水面AB 宽 20米,拱桥的最高点O到水面AB 的距离是 4 米,建立平面直角坐标系xOy如图,如果水面上升了1米,那么此时水面的宽度是______________米.(结果保留根号)
16.如图,A,B,C,D 四点在抛物线 上,且 ∥∥轴,与y轴的交点分别为点E,F,已知 求a的值及OF 的长.
参考答案
1. A 2. C 3. D 4. C 5. C
(2)向下 y轴 (0,2) 9.-1 10.-6
11.解:列表如表:
… -3 -2 -1 0 1 2 3 …
… -9 -4 -1 0 -1 -4 -9 …
… -8 -3 0 1 0 -3 -8 …
描点:表中的数据作为点的坐标在平面直角坐标系中描出,
连线:用平滑的线连接,如图所示:
(1)抛物线 向下平移1个单位得到抛物线
故答案为:下,1;
(2)抛物线 的图象开口向下,对称轴为 y轴,顶点坐标为(0,1).
故答案为:向下,y轴,(0,1);
(3)对抛物线 当 时,函数 y随x 的增大而减小;当 时,函数 y有最大值,其最大值是1.
故答案为:,大,大,1.
12.解:如图所示:
(1)抛物线的顶点坐标为(0,1),对称轴为y轴;
(2)当x<0时,y的值随x值的增大而增大;
(3)当x=0时,函数有最大值,最大值为1.
13.解:当x=0时, 则 A 点坐标为(0,3).
∥轴,∴B点,C点的纵坐标都为3.
当 时, 解得 ∴B(-3,3),C(3,3),
14. B 解析:过点 A 作. 轴于点 H,
∵四边形ABCO是正方形, ∴
设A(m,m),则 B(0,2m),
解得
∴ac的值为
解析:设抛物线的表达式为
∵O点到水面AB 的距离为 4 米,∴A,B点的纵坐标为
∵水面AB宽为20米,
将 A代入 得
∵水位上升1米,∴O点到水面的距离为 3,
把y=-3代入 得
∴水面的宽度为 米.
16.解:由题意可设点 ,
则 解得
∥轴,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
