第三章 二次函数 专项训练 二次函数图象与系数(含答案)
文档属性
| 名称 | 第三章 二次函数 专项训练 二次函数图象与系数(含答案) | 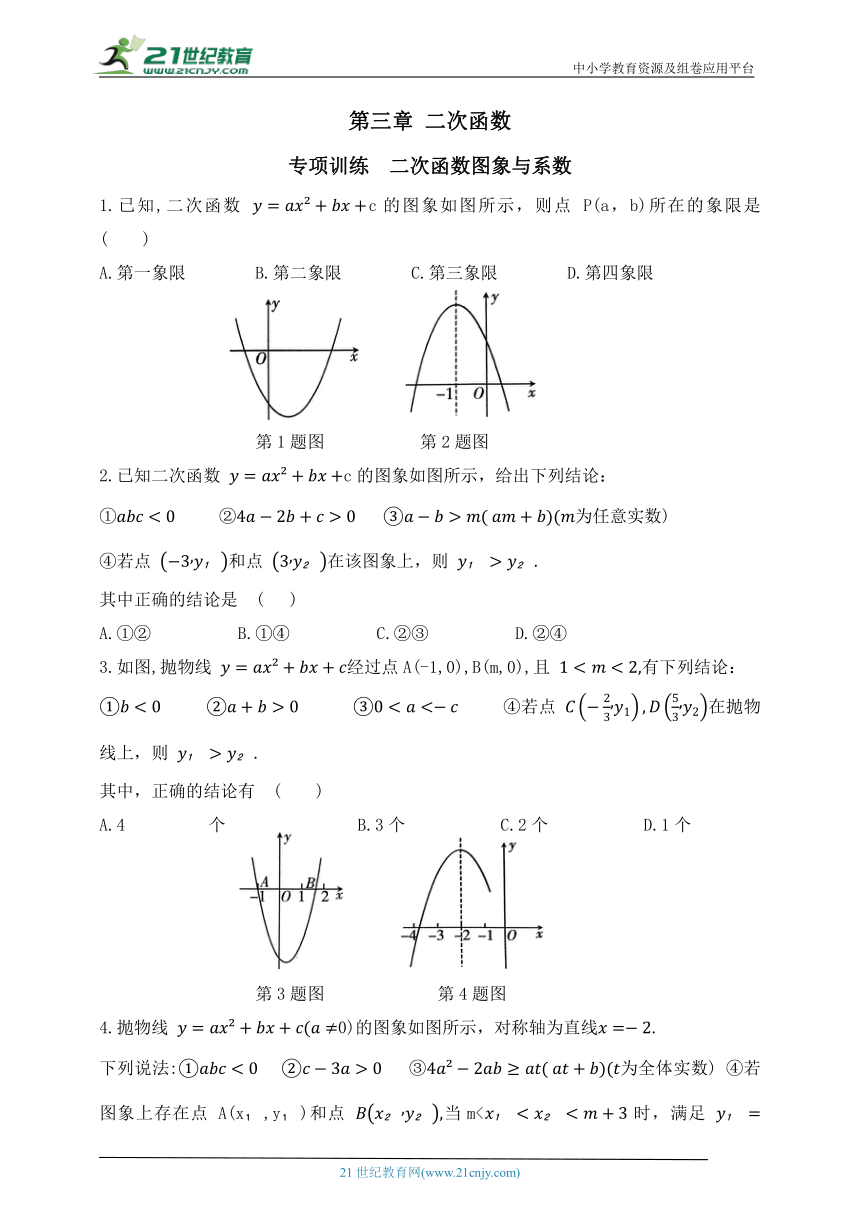 | |
| 格式 | docx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 15:40:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
二次函数
专项训练 二次函数图象与系数
1.已知,二次函数 c的图象如图所示,则点 P(a,b)所在的象限是 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
第1题图 第2题图
2.已知二次函数 c的图象如图所示,给出下列结论:
为任意实数)
④若点 和点 在该图象上,则
其中正确的结论是 ( )
A.①② B.①④ C.②③ D.②④
3.如图,抛物线 经过点A(-1,0),B(m,0),且 有下列结论:
④若点 在抛物线上,则
其中,正确的结论有 ( )
A.4个 B.3个 C.2个 D.1个
第3题图 第4题图
4.抛物线 0)的图象如图所示,对称轴为直线.
下列说法:为全体实数) ④若图象上存在点 A(x ,y )和点 当m<时,满足 则m的取值范围为-5A.1个 B.2个 C.3个 D.4个
5.如图,抛物线 (a,b,c 为常数)关于直线 对称.下列五个结论:.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
6.已知二次函数 (a为常数,且a>0),下列结论:①函数象一定经过第一、二、四象限 ②函数图象一定不经过第三象限 ③当x<0时,y随x的增大而减小 ④当x>0时,y随x的增大而增大.其中所有正确结论的序号是 ( )
A.①② B.②③ C.② D.③④
7.已知二次函数 的图象如图所示,其对称轴 为直线下列四个结论:④当 时, 其中正确的结论有 ( )
A.4个 B.3个 C.2个 D.1个
第7题图 第8题图
8.如图,抛物线 的对称轴是直线x=1,则下列五个结论: 其中正确结论的个数是 ( )
A.4个 B.3个 C.2个 D.1个
9.二次函数 的图象如图所示,对称轴是直线,下列结论:其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
第9题图 第10题图
10.二次函数 的部分图象如图所示,对称轴为直线下列结论: 其中正确的个数是 ( )
A.2个 B.3个 C.4个 D.5个
11.已知抛物线 的图象如图所示,那么点 P(b,c)在第_____象限.
第11题图 第12题图
12.已知抛物线(a,b,c 为常数,a≠0)的对称轴是直线,其部分图象如图所示,则下列四个结论中:其中,正确结论的序号是_________.
13.已知二次函数 的图象如图所示,其对称轴给出下列结论:.其中正确结论的序号是_________.
参考答案
1. D 2. D
3. B 解析:①∵抛物线开口向上,∴
∵抛物线的对称轴在 y轴的右侧,∴故①正确;
②∵抛物线与 y轴的交点在x轴下方,∴c<0,
∵抛物线经过点A(-1,0),∴a-b+c=0,∴c=b-a,
∵当x=2时,y>0,∴4a+2b+c>0,∴3a+3b>0,∴a+b>0,故②正确;
③∵a-b+c=0,∴a+c=b,
∵b<0,∴a+c<0,∴0④∵点 到对称轴的距离比点 到对称轴的距离近,
故④错误.
4. C 解析:①由图象开口向下,得a<0;
又∵对称轴为直线x=-2, 整理得b=4a,则b<0.
由图象,得当x=-4时,y<0,由图象,得当x=-4时,y<0,
又∵对称轴为直线x=-2,可知当x=0时,y<0,即c<0;
∴abc<0,故①正确;
②由图象,得当x=-1时,y=a-b+c>0,
由①,得b=4a,故a-4a+c>0,整理得c-3a>0,故②正确;
③设 则 4a-2b≤at·t+ bt,两边+c得到4a-2b+c≤at·t+ bt+c,左侧为x=-2时的函数值,右侧为x=t时的函数值,与图象相矛盾,故③错误;
④由题意,得 x ,x 是一元二次方程 的两个根,
从图象上看,因二次函数有对称性,则x ,x 关于x=-2 对称,
∴当且仅当m<-2当时,满足 故④正确.
5. B 6. B
7. A 解析:①由图象可知 1>0,∴b>0,∴abc<0,故①正确;
②∵对称轴为直线x=1, ∴2a+b=0,故②正确;
③当x=-1时,y<0,当x=1时,y>0,
故③正确;
④当 时,y的值最大.此时,
而当x=m时, 其中
所以
故 即 故④正确.
8. A 9. D
10. C 解析:
∵抛物线交 y轴的正半轴,∴c>0,∴abc>0,故①错误;
②故②正确;
③∵x=1时,y<0,∴a+b+c<0,故③正确;
④ ∴2a=3b,
又∵当x=-1时,y>0,∴a-b+c>0,∴2a-2b+2c>0,
,即b+2c>0,故④正确;
⑤∵抛物线开口向下,∴a<0,
∵ab>0,∴b<0,∴-2b>0.
∴a-2b+4c>0,故④正确.
11.二 12.②③④ 13.①④⑤
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
二次函数
专项训练 二次函数图象与系数
1.已知,二次函数 c的图象如图所示,则点 P(a,b)所在的象限是 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
第1题图 第2题图
2.已知二次函数 c的图象如图所示,给出下列结论:
为任意实数)
④若点 和点 在该图象上,则
其中正确的结论是 ( )
A.①② B.①④ C.②③ D.②④
3.如图,抛物线 经过点A(-1,0),B(m,0),且 有下列结论:
④若点 在抛物线上,则
其中,正确的结论有 ( )
A.4个 B.3个 C.2个 D.1个
第3题图 第4题图
4.抛物线 0)的图象如图所示,对称轴为直线.
下列说法:为全体实数) ④若图象上存在点 A(x ,y )和点 当m<时,满足 则m的取值范围为-5
5.如图,抛物线 (a,b,c 为常数)关于直线 对称.下列五个结论:.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
6.已知二次函数 (a为常数,且a>0),下列结论:①函数象一定经过第一、二、四象限 ②函数图象一定不经过第三象限 ③当x<0时,y随x的增大而减小 ④当x>0时,y随x的增大而增大.其中所有正确结论的序号是 ( )
A.①② B.②③ C.② D.③④
7.已知二次函数 的图象如图所示,其对称轴 为直线下列四个结论:④当 时, 其中正确的结论有 ( )
A.4个 B.3个 C.2个 D.1个
第7题图 第8题图
8.如图,抛物线 的对称轴是直线x=1,则下列五个结论: 其中正确结论的个数是 ( )
A.4个 B.3个 C.2个 D.1个
9.二次函数 的图象如图所示,对称轴是直线,下列结论:其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
第9题图 第10题图
10.二次函数 的部分图象如图所示,对称轴为直线下列结论: 其中正确的个数是 ( )
A.2个 B.3个 C.4个 D.5个
11.已知抛物线 的图象如图所示,那么点 P(b,c)在第_____象限.
第11题图 第12题图
12.已知抛物线(a,b,c 为常数,a≠0)的对称轴是直线,其部分图象如图所示,则下列四个结论中:其中,正确结论的序号是_________.
13.已知二次函数 的图象如图所示,其对称轴给出下列结论:.其中正确结论的序号是_________.
参考答案
1. D 2. D
3. B 解析:①∵抛物线开口向上,∴
∵抛物线的对称轴在 y轴的右侧,∴故①正确;
②∵抛物线与 y轴的交点在x轴下方,∴c<0,
∵抛物线经过点A(-1,0),∴a-b+c=0,∴c=b-a,
∵当x=2时,y>0,∴4a+2b+c>0,∴3a+3b>0,∴a+b>0,故②正确;
③∵a-b+c=0,∴a+c=b,
∵b<0,∴a+c<0,∴0
故④错误.
4. C 解析:①由图象开口向下,得a<0;
又∵对称轴为直线x=-2, 整理得b=4a,则b<0.
由图象,得当x=-4时,y<0,由图象,得当x=-4时,y<0,
又∵对称轴为直线x=-2,可知当x=0时,y<0,即c<0;
∴abc<0,故①正确;
②由图象,得当x=-1时,y=a-b+c>0,
由①,得b=4a,故a-4a+c>0,整理得c-3a>0,故②正确;
③设 则 4a-2b≤at·t+ bt,两边+c得到4a-2b+c≤at·t+ bt+c,左侧为x=-2时的函数值,右侧为x=t时的函数值,与图象相矛盾,故③错误;
④由题意,得 x ,x 是一元二次方程 的两个根,
从图象上看,因二次函数有对称性,则x ,x 关于x=-2 对称,
∴当且仅当m<-2
5. B 6. B
7. A 解析:①由图象可知 1>0,∴b>0,∴abc<0,故①正确;
②∵对称轴为直线x=1, ∴2a+b=0,故②正确;
③当x=-1时,y<0,当x=1时,y>0,
故③正确;
④当 时,y的值最大.此时,
而当x=m时, 其中
所以
故 即 故④正确.
8. A 9. D
10. C 解析:
∵抛物线交 y轴的正半轴,∴c>0,∴abc>0,故①错误;
②故②正确;
③∵x=1时,y<0,∴a+b+c<0,故③正确;
④ ∴2a=3b,
又∵当x=-1时,y>0,∴a-b+c>0,∴2a-2b+2c>0,
,即b+2c>0,故④正确;
⑤∵抛物线开口向下,∴a<0,
∵ab>0,∴b<0,∴-2b>0.
∴a-2b+4c>0,故④正确.
11.二 12.②③④ 13.①④⑤
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
