第三章 二次函数 专项训练 二次函数与几何图形综合(含答案)
文档属性
| 名称 | 第三章 二次函数 专项训练 二次函数与几何图形综合(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 07:32:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
专项训练 二次函数与几何图形综合
一 二次函数与线段
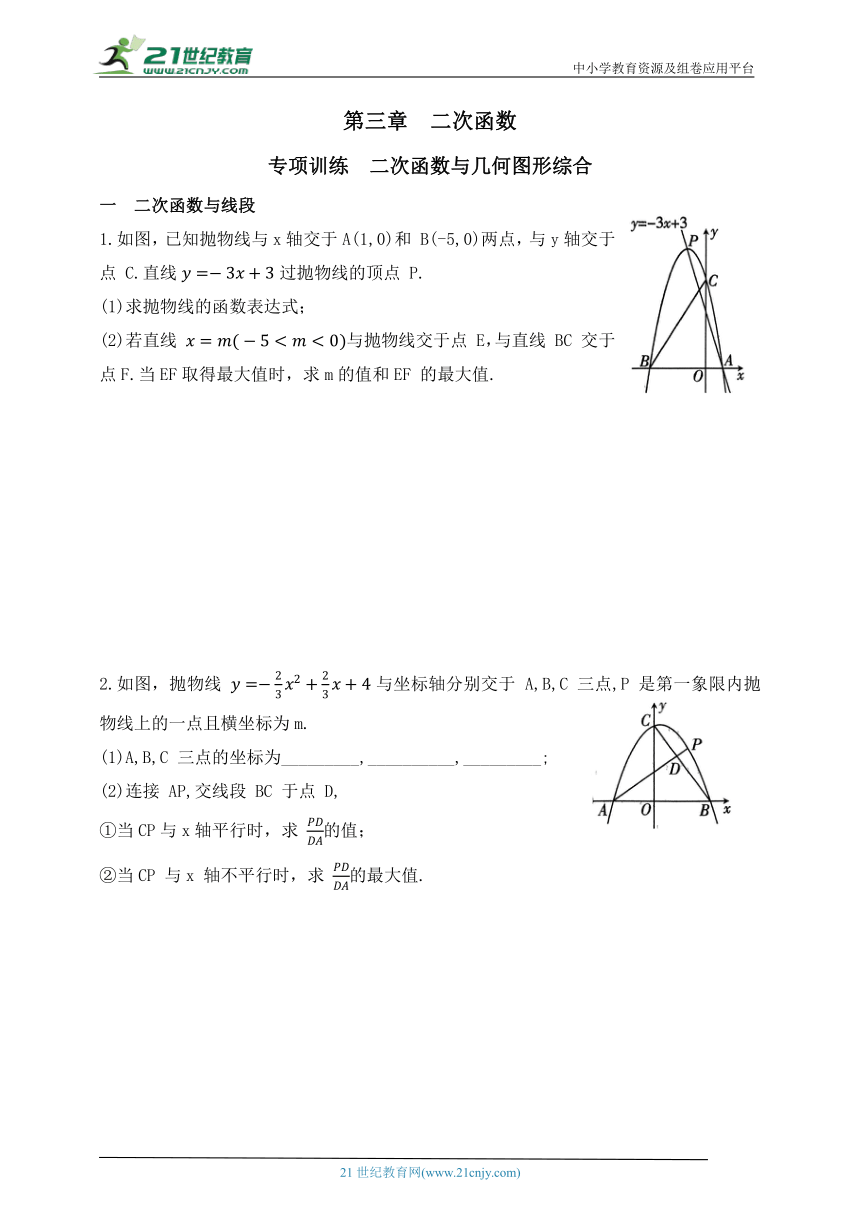
1.如图,已知抛物线与x轴交于A(1,0)和 B(-5,0)两点,与y轴交于点 C.直线过抛物线的顶点 P.
(1)求抛物线的函数表达式;
(2)若直线 与抛物线交于点 E,与直线 BC 交于点F.当EF取得最大值时,求m的值和EF 的最大值.
2.如图,抛物线 与坐标轴分别交于 A,B,C 三点,P 是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C 三点的坐标为_________,__________,_________;
(2)连接 AP,交线段 BC 于点 D,
①当CP与x轴平行时,求 的值;
②当CP 与x 轴不平行时,求 的最大值.
3.如图,二次函数 的图象与x 轴的正半轴交于点A,经过点 A 的直线与该函数图象交于点 B(1,3),与 y轴交于点C.
(1)求直线 AB 的函数表达式及点 C 的坐标;
(2)点P 是第一象限内二次函数图象上的一个动点,过点 P 作直线. 轴于点E,与直线 AB 交于点 D,设点 P 的横坐标为m.当 时,求m的值.
二 二次函数与面积(最值,定值)
4.如图,抛物线 c过点 点 B(5,0),交 y轴于点 C.
(1)求 b,c的值;
(2)点 是抛物线上的动点.当 取何值时,的面积最大 并求出 面积的最大值.
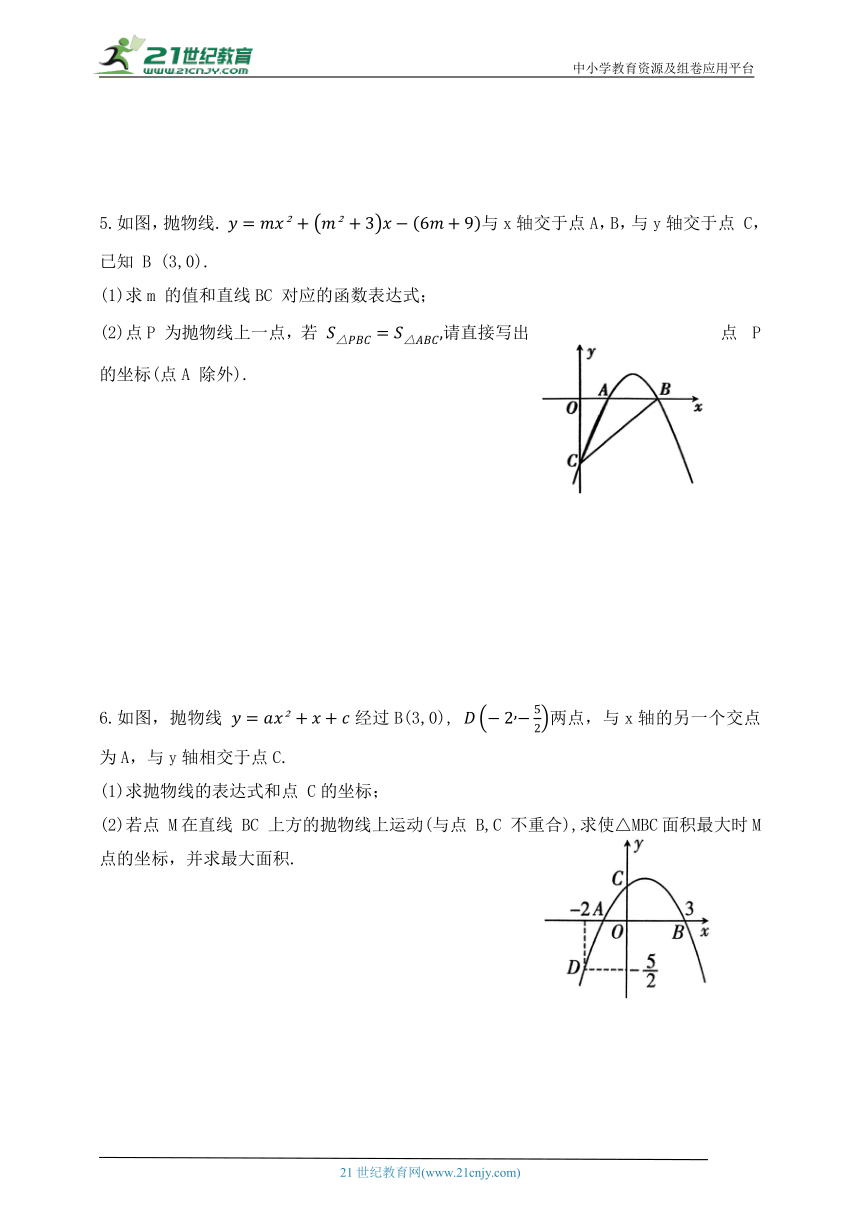
5.如图,抛物线. 与x轴交于点A,B,与y轴交于点 C,已知 B (3,0).
(1)求m 的值和直线BC 对应的函数表达式;
(2)点P 为抛物线上一点,若 请直接写出点 P 的坐标(点A 除外).
6.如图,抛物线 经过B(3,0), 两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的表达式和点 C的坐标;
(2)若点 M在直线 BC 上方的抛物线上运动(与点 B,C 不重合),求使△MBC面积最大时M 点的坐标,并求最大面积.
三 二次函数与图形存在性
7.如图,抛物线 经过 C(0,3)两点,并交 x 轴于另一点 B,点M 是抛物线的顶点,直线 AM与y 轴交于点 D.
(1)求该抛物线的表达式;
(2)若点 H 是 x 轴上一动点,分别连接MH,DH,求. 的最小值;
(3)若点 P 是抛物线上一动点,问在对称轴上是否存在点 Q,使得以D,M,P,Q为顶点的四边形是平行四边形 若存在,请直接写出所有满足条件的点 Q的坐标;若不存在,请说明理由.
8.如图,二次函数 c的图象交x 轴于点A,B,交 y轴于点C,点 B的坐标为(1,0),对称轴是直线. 点 P 是x 轴上一动点, 轴,交直线AC 于点 M,交抛物线于点 N.
(1)求这个二次函数的表达式;
(2)若点 P 在线段AO 上运动(点 P 与点A,点 O不重合),求四边形 ABCN面积的最大值,并求出此时点 P 的坐标;
(3)若点 P在x 轴上运动,则在 y轴上是否存在点Q,使以 M,N,C,Q为顶点的四边形是菱形 若存在,请直接写出所有满足条件的点 Q的坐标;若不存在,请说明理由.
9.已知抛物线 与x轴交于A(-2,0),B(6,0)两点,与y轴交于点
(1)求抛物线的表达式;
(2)点P 在直线BC 下方的抛物线上,连接AP 交 BC 于点M,当 最大时,求点 P 的坐标;
(3)在(2)的条件下,过点 P 作 x 轴的垂线,在上是否存在点D,使 是直角三角形,若存在,请求出点 D 的坐标;若不存在,请说明理由.
10.如图,点 C 为二次函数 的顶点,直线 与该二次函数图象交于 4),B两点(点B 在y 轴上),与二次函数图象的对称轴交于点 D.
(1)求 m 的值及点C 坐标;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)连接AC,BC,求 的面积;
(4)在该二次函数的对称轴上是否存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形 若存在,直接写出符合条件的Q点的坐标;若不存在,请说明理由.
参考答案
1.解:(1)∵ 抛物线 与 x 轴交 于 A(1,0) 和两点,
∴抛物线对称轴为直线 在 中,令 得
∴抛物线顶点 P 为(
设抛物线函数表达式为
将 A(1,0)代入,得( 解得
∴抛物线函数表达式为
(2)如图,
在 中,令 得 ∴C(0,5),
由 B(-5,0),C(0,5),得直线 BC 表达式为
∵-1<0,∴当 时,EF 取最大值
∴m的值为 EF的最大值为
2.解:(1)令x=0,则y=4,∴C(0,4).
令 y=0,则 解得x=-2 或x=3,
∴A(-2,0),B(3,0).
故答案为:(-2,0),(3,0),(0,4);
(2)①∵CP∥x轴,C(0,4),抛物线对称轴为直线
∴P(1,4),
∥轴,
②如图,过点 P 作 ∥交 BC于点Q.
∵B(3,0),C(0,4),∴直线 BC的表达式为 ∵点 P 的横坐标为m,
∥
∴当 时, 的最大值为
(另一种解法:分别过点 P,A作 y轴的平行线,交直线 BC于两点,仿照以上解法即可求解)
3.解:(1)由 得当 时,解得
∵点 A 在x 轴正半轴上,∴点 A的坐标为(4,0).
设直线AB的函数表达式为
将 A,B两点的坐标(4,0),(1,3)分别代入
得 解得
∴直线AB的函数表达式为
将x=0代入y=-x+4,得y=4.∴点C的坐标为(0,4);
(2)由题意,设
∵点C的坐标为(0,4),
①如图1,当点 P在直线上方时,
图1
解得
②如图2,当点 P 在直线AB下方时,
图2
解得
综上所述,m的值为2或3 或
4.解:(1)∵抛物线 过点A(-1, 0),B(5,0),
∴抛物线的表达式为 ∴b=-4,c=-5;
(2)由(1),得抛物线的表达式为 令x=0,则y=-5;
∴C(0,-5)∴直线 BC的表达式为
如图,过点 P 作 x 轴的垂线,交线段 BC于点D,则
∴当 时,S的值取最大,最大值为
5.解:(1)将 B(3,0)代入 (6m+9),化简,得
则m=0(舍)或m=-1,∴m==1,
设直线 BC的函数表达式为
将 B(3,0),C(0,-3)代入,得 解得
∴直线 BC的函数表达式为
(2)如图,过点 A 作 ∥设直线交y轴于点G,将直线 BC 向下平移GC个单位,得到直线 直线 与 y轴交于点 H,则
①由(1),得直线 BC的表达式为 A(1,0),
∴直线AG的表达式为
联立 解得 (舍)或
②由直线 AG的表达式可得(
又∵C(0,-3),
∴直线 的表达式为
联立 解得 或
综上所述,符合题意的点 P 的坐标为(2,1),
6.解:(1)将 B(3,0), 代入
得 解得
令x=0,则
(2)作直线 BC,过M点作 MN∥y轴交 BC 于点 N,连接CM,BM.
设直线 BC 的表达式为
将 B(3,0), 代入,得 解得
设 则 N(m,
当 时, 的面积有最大值 此时
7.解:(1)∵抛物线 经过A(-1,0),C(0,3)两点,
解得
∴该抛物线的表达式为
∴顶点 M(1,4),
又 设直线 AM 的表 达 式为
则 解得
∴直线AM的表达式为
当x=0时,y=2,∴D(0,2),
作点 D关于x 轴的对称点. 连接D'M,D'H,如图,
则DH=D'H,即 的最小值为
的最小值为
(3)对称轴上存在点 Q,使得以 D,M,P,Q为顶点的四边形是平行四边形.
由(2),得 D(0,2),M(1,4),
∵点P 是抛物线上一动点,∴设
∵抛物线 的对称轴为直线x=1,
∴设Q(1,n),
①当 DM,PQ 为对角线时,DM,PQ 的中点重合,
解得 ∴Q(1,3);
②当 DP,MQ 为对角线时,DP,MQ 的中点重合,
解得 ∴Q(1,1);
③当 DQ,PM 为对角线时,DQ,PM 的中点重合,
解得 ∴Q(1,5);
综上所述,对称轴上存在点 Q,使得以 D,M,P,Q为顶点的四边形是平行四边形,点Q 的坐标为(1,3)或(1,1)或(1,5).
8.解:(1)∵抛物线对称轴是直线x=-1,点 B的坐标为(1,0),
∴点 A 的坐标为(
∴二次函数表达式为
(2)连接ON,如图,
设 P(m,0),则 N(m,
在 中,令x=0得 y=-3,
3·(-m)
∴当 时, 取最大值 此时
∴四边形 ABCN 面积的最大值是 此时点P的坐标为
(3)在 y轴上存在点Q,使以 M,N,C,Q 为顶点的四边形是菱形,理由:
由 得直线 AC表达式为
设 Q(0,t),P(n,0),则 M(n,-n-3),N(n,
∥∴当M,N,C,Q为顶点的四边形是菱形时,MN,CQ 是一组对边;
①当MC,NQ为对角线时,MC,NQ的中点重合,且CN=CQ,
解得
(此时 M,N与C 重合,舍去)或
②当MQ,CN 为对角线时,MQ,CN 的中点重合,且 CQ=CM,
解得 ( 舍去) 或 或
或
综上所述,Q的坐标为 或 或
9.解:(1)将点 A(-2,0),B(6,0),C(0,-3)代入
得 解得
(2)如图1,过点 A 作. 轴交直线 BC 于点 E,过 P 作 轴交直线BC于点F, ∥
设直线 BC的表达式为
设 则
∴当 3时, 有最大值
D 点在上,
①如图2,当 时,过点 B 作 轴,过点 D 作 轴,DG与GH交于点G,过点 C作 轴,CH与GH交于点 H,
90°,∴∠GDB=∠CBH,
∴△DBG∽△BCH, 即 ∴BG=6,∴D(3,6);
②如图3,当∠BCD=90°时,过点 D 作 DK⊥y 轴于点 K,
∵∠KCD +∠OCB =90°,∠KCD+∠CDK=90°,∴∠CDK=∠OCB,
∴△OBC∽△KCD, 即 ∴KC=6,∴D(3,-9);
③如图4,当∠BDC=90°时,线段 BC的中点 设 D(3,m),
或 m=
或
综上所述,△BCD 是直角三角形时,D点坐标为(3,6)或(3,-9)或 或
10.解:(1)∵直线 y=-x+m过点A(-3,4),∴4=3+m,∴m=1,∴y=-x+1;
二次函数表达式为 1) ,顶点坐标为C(-1,0);
(2)将x=0代入 得 y=1,∴B(0,1),且A(-3,4),
由图象,得一次函数值大于二次函数值的x的取值范围为-3(3)由(1),得直线 AB 的表达式为y=-x+1,C(-1,0),二次函数对称轴为x=-1,
∴点 D(-1,a),∴a=-1×(-1)+1=2,∴D(-1,2),∴CD=2,
的面积
(4)存在.∵顶点坐标为∴对称轴为 ∴设点
又 点
①当 AC= AQ 时,则
(舍去),∴点 Q坐标为(
②当AC=CQ时,则
∴点 Q 坐标为( 或
③当AQ=CQ时,则(
∴点 Q 坐标为
综上所述,点Q 的坐标为( 或 或 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
专项训练 二次函数与几何图形综合
一 二次函数与线段
1.如图,已知抛物线与x轴交于A(1,0)和 B(-5,0)两点,与y轴交于点 C.直线过抛物线的顶点 P.
(1)求抛物线的函数表达式;
(2)若直线 与抛物线交于点 E,与直线 BC 交于点F.当EF取得最大值时,求m的值和EF 的最大值.
2.如图,抛物线 与坐标轴分别交于 A,B,C 三点,P 是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C 三点的坐标为_________,__________,_________;
(2)连接 AP,交线段 BC 于点 D,
①当CP与x轴平行时,求 的值;
②当CP 与x 轴不平行时,求 的最大值.
3.如图,二次函数 的图象与x 轴的正半轴交于点A,经过点 A 的直线与该函数图象交于点 B(1,3),与 y轴交于点C.
(1)求直线 AB 的函数表达式及点 C 的坐标;
(2)点P 是第一象限内二次函数图象上的一个动点,过点 P 作直线. 轴于点E,与直线 AB 交于点 D,设点 P 的横坐标为m.当 时,求m的值.
二 二次函数与面积(最值,定值)
4.如图,抛物线 c过点 点 B(5,0),交 y轴于点 C.
(1)求 b,c的值;
(2)点 是抛物线上的动点.当 取何值时,的面积最大 并求出 面积的最大值.
5.如图,抛物线. 与x轴交于点A,B,与y轴交于点 C,已知 B (3,0).
(1)求m 的值和直线BC 对应的函数表达式;
(2)点P 为抛物线上一点,若 请直接写出点 P 的坐标(点A 除外).
6.如图,抛物线 经过B(3,0), 两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的表达式和点 C的坐标;
(2)若点 M在直线 BC 上方的抛物线上运动(与点 B,C 不重合),求使△MBC面积最大时M 点的坐标,并求最大面积.
三 二次函数与图形存在性
7.如图,抛物线 经过 C(0,3)两点,并交 x 轴于另一点 B,点M 是抛物线的顶点,直线 AM与y 轴交于点 D.
(1)求该抛物线的表达式;
(2)若点 H 是 x 轴上一动点,分别连接MH,DH,求. 的最小值;
(3)若点 P 是抛物线上一动点,问在对称轴上是否存在点 Q,使得以D,M,P,Q为顶点的四边形是平行四边形 若存在,请直接写出所有满足条件的点 Q的坐标;若不存在,请说明理由.
8.如图,二次函数 c的图象交x 轴于点A,B,交 y轴于点C,点 B的坐标为(1,0),对称轴是直线. 点 P 是x 轴上一动点, 轴,交直线AC 于点 M,交抛物线于点 N.
(1)求这个二次函数的表达式;
(2)若点 P 在线段AO 上运动(点 P 与点A,点 O不重合),求四边形 ABCN面积的最大值,并求出此时点 P 的坐标;
(3)若点 P在x 轴上运动,则在 y轴上是否存在点Q,使以 M,N,C,Q为顶点的四边形是菱形 若存在,请直接写出所有满足条件的点 Q的坐标;若不存在,请说明理由.
9.已知抛物线 与x轴交于A(-2,0),B(6,0)两点,与y轴交于点
(1)求抛物线的表达式;
(2)点P 在直线BC 下方的抛物线上,连接AP 交 BC 于点M,当 最大时,求点 P 的坐标;
(3)在(2)的条件下,过点 P 作 x 轴的垂线,在上是否存在点D,使 是直角三角形,若存在,请求出点 D 的坐标;若不存在,请说明理由.
10.如图,点 C 为二次函数 的顶点,直线 与该二次函数图象交于 4),B两点(点B 在y 轴上),与二次函数图象的对称轴交于点 D.
(1)求 m 的值及点C 坐标;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)连接AC,BC,求 的面积;
(4)在该二次函数的对称轴上是否存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形 若存在,直接写出符合条件的Q点的坐标;若不存在,请说明理由.
参考答案
1.解:(1)∵ 抛物线 与 x 轴交 于 A(1,0) 和两点,
∴抛物线对称轴为直线 在 中,令 得
∴抛物线顶点 P 为(
设抛物线函数表达式为
将 A(1,0)代入,得( 解得
∴抛物线函数表达式为
(2)如图,
在 中,令 得 ∴C(0,5),
由 B(-5,0),C(0,5),得直线 BC 表达式为
∵-1<0,∴当 时,EF 取最大值
∴m的值为 EF的最大值为
2.解:(1)令x=0,则y=4,∴C(0,4).
令 y=0,则 解得x=-2 或x=3,
∴A(-2,0),B(3,0).
故答案为:(-2,0),(3,0),(0,4);
(2)①∵CP∥x轴,C(0,4),抛物线对称轴为直线
∴P(1,4),
∥轴,
②如图,过点 P 作 ∥交 BC于点Q.
∵B(3,0),C(0,4),∴直线 BC的表达式为 ∵点 P 的横坐标为m,
∥
∴当 时, 的最大值为
(另一种解法:分别过点 P,A作 y轴的平行线,交直线 BC于两点,仿照以上解法即可求解)
3.解:(1)由 得当 时,解得
∵点 A 在x 轴正半轴上,∴点 A的坐标为(4,0).
设直线AB的函数表达式为
将 A,B两点的坐标(4,0),(1,3)分别代入
得 解得
∴直线AB的函数表达式为
将x=0代入y=-x+4,得y=4.∴点C的坐标为(0,4);
(2)由题意,设
∵点C的坐标为(0,4),
①如图1,当点 P在直线上方时,
图1
解得
②如图2,当点 P 在直线AB下方时,
图2
解得
综上所述,m的值为2或3 或
4.解:(1)∵抛物线 过点A(-1, 0),B(5,0),
∴抛物线的表达式为 ∴b=-4,c=-5;
(2)由(1),得抛物线的表达式为 令x=0,则y=-5;
∴C(0,-5)∴直线 BC的表达式为
如图,过点 P 作 x 轴的垂线,交线段 BC于点D,则
∴当 时,S的值取最大,最大值为
5.解:(1)将 B(3,0)代入 (6m+9),化简,得
则m=0(舍)或m=-1,∴m==1,
设直线 BC的函数表达式为
将 B(3,0),C(0,-3)代入,得 解得
∴直线 BC的函数表达式为
(2)如图,过点 A 作 ∥设直线交y轴于点G,将直线 BC 向下平移GC个单位,得到直线 直线 与 y轴交于点 H,则
①由(1),得直线 BC的表达式为 A(1,0),
∴直线AG的表达式为
联立 解得 (舍)或
②由直线 AG的表达式可得(
又∵C(0,-3),
∴直线 的表达式为
联立 解得 或
综上所述,符合题意的点 P 的坐标为(2,1),
6.解:(1)将 B(3,0), 代入
得 解得
令x=0,则
(2)作直线 BC,过M点作 MN∥y轴交 BC 于点 N,连接CM,BM.
设直线 BC 的表达式为
将 B(3,0), 代入,得 解得
设 则 N(m,
当 时, 的面积有最大值 此时
7.解:(1)∵抛物线 经过A(-1,0),C(0,3)两点,
解得
∴该抛物线的表达式为
∴顶点 M(1,4),
又 设直线 AM 的表 达 式为
则 解得
∴直线AM的表达式为
当x=0时,y=2,∴D(0,2),
作点 D关于x 轴的对称点. 连接D'M,D'H,如图,
则DH=D'H,即 的最小值为
的最小值为
(3)对称轴上存在点 Q,使得以 D,M,P,Q为顶点的四边形是平行四边形.
由(2),得 D(0,2),M(1,4),
∵点P 是抛物线上一动点,∴设
∵抛物线 的对称轴为直线x=1,
∴设Q(1,n),
①当 DM,PQ 为对角线时,DM,PQ 的中点重合,
解得 ∴Q(1,3);
②当 DP,MQ 为对角线时,DP,MQ 的中点重合,
解得 ∴Q(1,1);
③当 DQ,PM 为对角线时,DQ,PM 的中点重合,
解得 ∴Q(1,5);
综上所述,对称轴上存在点 Q,使得以 D,M,P,Q为顶点的四边形是平行四边形,点Q 的坐标为(1,3)或(1,1)或(1,5).
8.解:(1)∵抛物线对称轴是直线x=-1,点 B的坐标为(1,0),
∴点 A 的坐标为(
∴二次函数表达式为
(2)连接ON,如图,
设 P(m,0),则 N(m,
在 中,令x=0得 y=-3,
3·(-m)
∴当 时, 取最大值 此时
∴四边形 ABCN 面积的最大值是 此时点P的坐标为
(3)在 y轴上存在点Q,使以 M,N,C,Q 为顶点的四边形是菱形,理由:
由 得直线 AC表达式为
设 Q(0,t),P(n,0),则 M(n,-n-3),N(n,
∥∴当M,N,C,Q为顶点的四边形是菱形时,MN,CQ 是一组对边;
①当MC,NQ为对角线时,MC,NQ的中点重合,且CN=CQ,
解得
(此时 M,N与C 重合,舍去)或
②当MQ,CN 为对角线时,MQ,CN 的中点重合,且 CQ=CM,
解得 ( 舍去) 或 或
或
综上所述,Q的坐标为 或 或
9.解:(1)将点 A(-2,0),B(6,0),C(0,-3)代入
得 解得
(2)如图1,过点 A 作. 轴交直线 BC 于点 E,过 P 作 轴交直线BC于点F, ∥
设直线 BC的表达式为
设 则
∴当 3时, 有最大值
D 点在上,
①如图2,当 时,过点 B 作 轴,过点 D 作 轴,DG与GH交于点G,过点 C作 轴,CH与GH交于点 H,
90°,∴∠GDB=∠CBH,
∴△DBG∽△BCH, 即 ∴BG=6,∴D(3,6);
②如图3,当∠BCD=90°时,过点 D 作 DK⊥y 轴于点 K,
∵∠KCD +∠OCB =90°,∠KCD+∠CDK=90°,∴∠CDK=∠OCB,
∴△OBC∽△KCD, 即 ∴KC=6,∴D(3,-9);
③如图4,当∠BDC=90°时,线段 BC的中点 设 D(3,m),
或 m=
或
综上所述,△BCD 是直角三角形时,D点坐标为(3,6)或(3,-9)或 或
10.解:(1)∵直线 y=-x+m过点A(-3,4),∴4=3+m,∴m=1,∴y=-x+1;
二次函数表达式为 1) ,顶点坐标为C(-1,0);
(2)将x=0代入 得 y=1,∴B(0,1),且A(-3,4),
由图象,得一次函数值大于二次函数值的x的取值范围为-3
∴点 D(-1,a),∴a=-1×(-1)+1=2,∴D(-1,2),∴CD=2,
的面积
(4)存在.∵顶点坐标为∴对称轴为 ∴设点
又 点
①当 AC= AQ 时,则
(舍去),∴点 Q坐标为(
②当AC=CQ时,则
∴点 Q 坐标为( 或
③当AQ=CQ时,则(
∴点 Q 坐标为
综上所述,点Q 的坐标为( 或 或 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
