北师大版六上第1课时 整理与复习(1) 课件
文档属性
| 名称 | 北师大版六上第1课时 整理与复习(1) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
整理与复习(1)
(北师大版)六年级
上
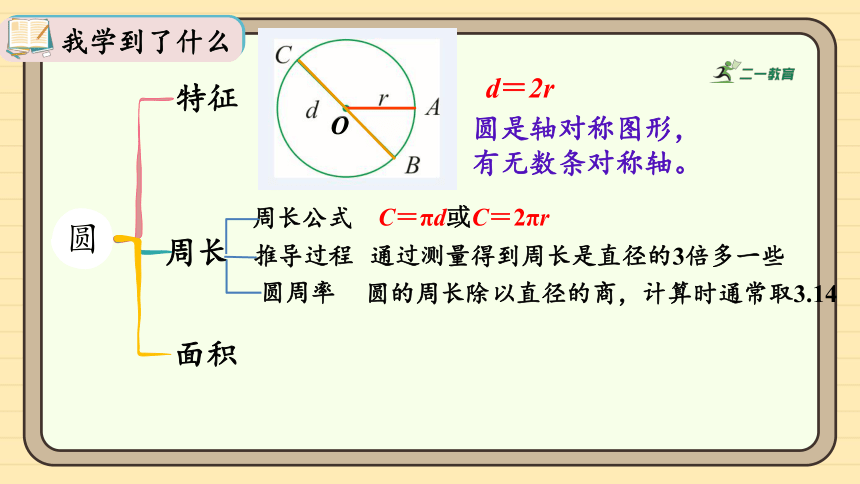
特征
圆
周长
面积
O
d=2r
圆是轴对称图形,有无数条对称轴。
我学到了什么
圆周率
圆的周长除以直径的商,计算时通常取3.14
C=πd或C=2πr
周长公式
推导过程
通过测量得到周长是直径的3倍多一些
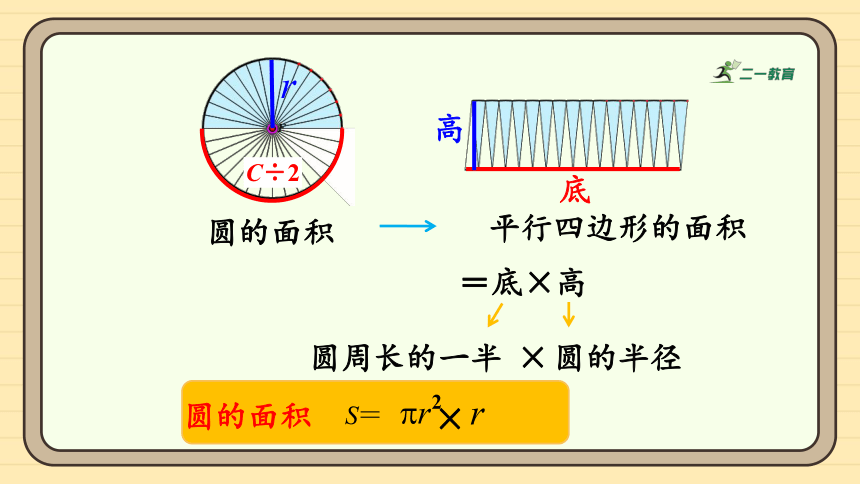
C÷2
底
高
圆的面积
圆周长的一半
=底×高
平行四边形的面积
圆的半径
×
×
圆的面积
2
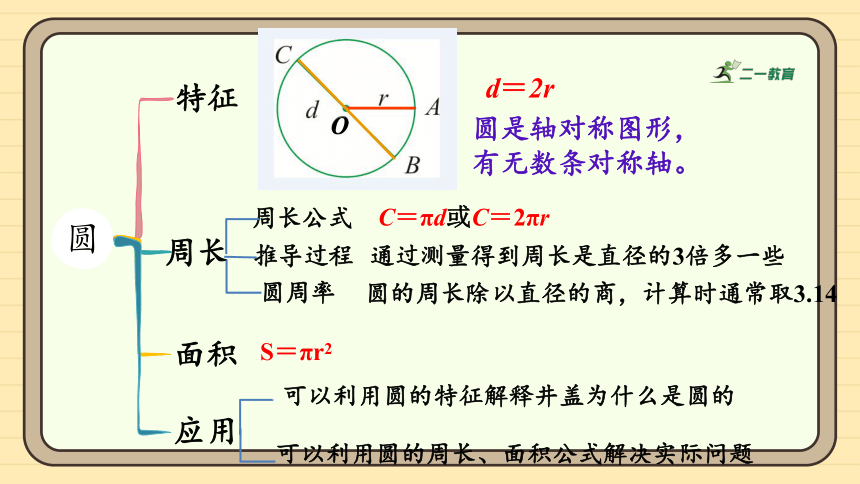
特征
圆
周长
面积
应用
O
d=2r
圆是轴对称图形,有无数条对称轴。
S=πr2
C=πd或C=2πr
周长公式
推导过程
通过测量得到周长是直径的3倍多一些
圆周率
圆的周长除以直径的商,计算时通常取3.14
可以利用圆的特征解释井盖为什么是圆的
可以利用圆的周长、面积公式解决实际问题
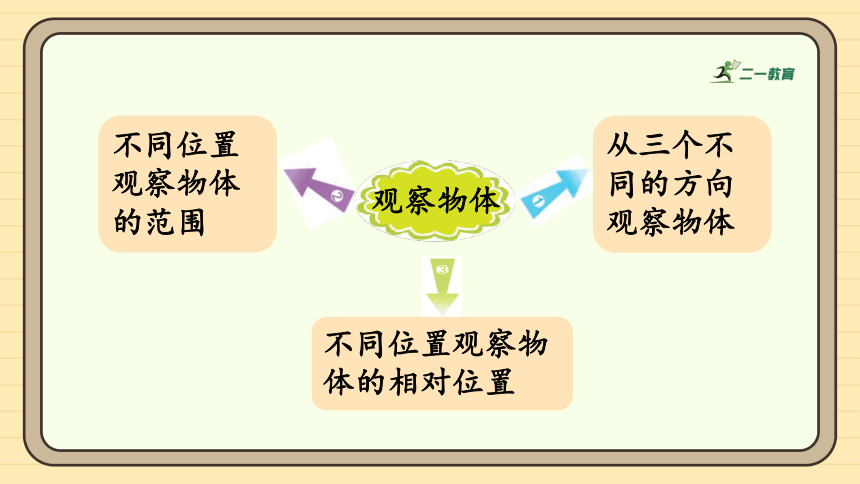
从三个不同的方向观察物体
不同位置观察物体的范围
不同位置观察物体的相对位置
观察物体
巩固应用
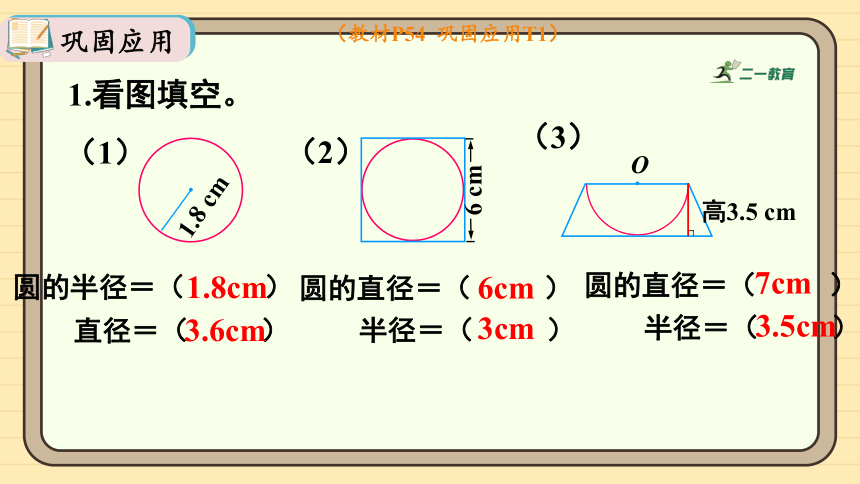
1.看图填空。
1.8 cm
(1)
圆的半径=( )
直径=( )
6 cm
(2)
圆的直径=( )
半径=( )
(3)
高3.5 cm
O
1.8cm
3.6cm
6cm
3cm
7cm
圆的直径=( )
半径=( )
3.5cm
(教材P54 巩固应用T1)
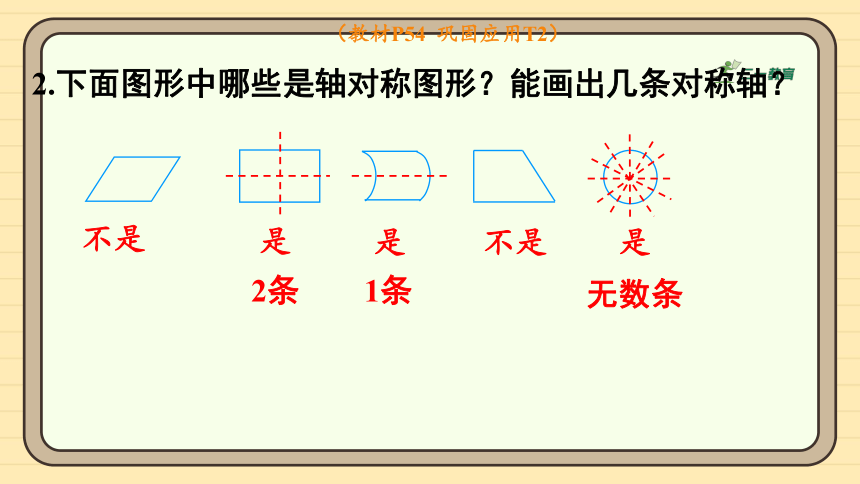
(教材P54 巩固应用T2)
2.下面图形中哪些是轴对称图形?能画出几条对称轴?
不是
是
是
不是
是
2条
1条
无数条
3.根据下面的条件,求各圆的面积。
(1)3.14×4 =50.24(cm )
(2)3.14×(1.4÷2) =1.5386(dm )
(3)6.28÷3.14÷2=1(cm)
3.14×1 =3.14(cm )
(1)r=4cm;(2)d=1.4dm ; (3)C=6.28cm。
(教材P54 巩固应用T3)
4.用小正方体搭成一个立体图形,画出从正面、上面、左面看到的形状。
正面
上面
左面
(教材P54 巩固应用T4)
5.两辆汽车从摄影师面前开过,摄影师依次拍摄了以下三幅照片。请你用序号标出摄影师的拍摄顺序。
①
②
③
(教材P54 巩固应用T5)
6.一根铁丝可以围成一个半径是3cm的圆,如果用它围成一个等边三角形,那么每边的长是多少厘米?
(教材P56 巩固应用T14)
2×3.14×3=18.84(cm)
18.84÷3=6.28(cm)
答:每边的长是6.28厘米。
7.下面是一个数学兴趣小组用一根长20dm的铁丝围图形的情况记录。
图形 周长/dm 长/dm 宽/dm 面积/dm2
长 方 形 20 9 1 9
20 8 2 16
20 7 3 21
20 6 4 24
20 5 5 25
圆 20 约31.85
(教材P56 巩固应用T15)
(1)分析以上实验记录,你发现了什么?
在周长相等的情况下,圆的面积大于长方形的面积。
(2)用上面的发现解释为什么排水管的
横截面都是圆形的。
所有材料相同的情况下,横截面是圆形,面积最大,排水最快。
8.求阴影部分的面积。
(教材P56 巩固应用T16)
(1)
梯形:(4+6)×4÷2= 20(cm2)
半圆:3.14×(4÷2)2÷2=6.28(cm2)
阴影部分:20-6.28=13.72(cm )
正方形:
20×20=400(cm2)
阴影部分:
400-314=86(cm2)
10cm
20cm
(2)
圆:
3.14×102=314(cm2)
9.银河广场有一个圆形喷水池,周长43.96m,有一条3m宽的小路围着喷水池,这条小路的面积是多少?
喷水池
小路
43.96÷3.14÷2 =7(m)
大圆的面积-小圆的面积=小路的面积
3.14×(7+3)2=314(m2)
3.14×72=153.86(m2)
314-153.86=160.14(m2)
答:这条小路的面积是160.14平方米。
3m
(教材P56 巩固应用T17)
情境导入
课堂小结
通过这节课的学习,你有什么收获
https://www.21cnjy.com/recruitment/home/fine
整理与复习(1)
(北师大版)六年级
上
特征
圆
周长
面积
O
d=2r
圆是轴对称图形,有无数条对称轴。
我学到了什么
圆周率
圆的周长除以直径的商,计算时通常取3.14
C=πd或C=2πr
周长公式
推导过程
通过测量得到周长是直径的3倍多一些
C÷2
底
高
圆的面积
圆周长的一半
=底×高
平行四边形的面积
圆的半径
×
×
圆的面积
2
特征
圆
周长
面积
应用
O
d=2r
圆是轴对称图形,有无数条对称轴。
S=πr2
C=πd或C=2πr
周长公式
推导过程
通过测量得到周长是直径的3倍多一些
圆周率
圆的周长除以直径的商,计算时通常取3.14
可以利用圆的特征解释井盖为什么是圆的
可以利用圆的周长、面积公式解决实际问题
从三个不同的方向观察物体
不同位置观察物体的范围
不同位置观察物体的相对位置
观察物体
巩固应用
1.看图填空。
1.8 cm
(1)
圆的半径=( )
直径=( )
6 cm
(2)
圆的直径=( )
半径=( )
(3)
高3.5 cm
O
1.8cm
3.6cm
6cm
3cm
7cm
圆的直径=( )
半径=( )
3.5cm
(教材P54 巩固应用T1)
(教材P54 巩固应用T2)
2.下面图形中哪些是轴对称图形?能画出几条对称轴?
不是
是
是
不是
是
2条
1条
无数条
3.根据下面的条件,求各圆的面积。
(1)3.14×4 =50.24(cm )
(2)3.14×(1.4÷2) =1.5386(dm )
(3)6.28÷3.14÷2=1(cm)
3.14×1 =3.14(cm )
(1)r=4cm;(2)d=1.4dm ; (3)C=6.28cm。
(教材P54 巩固应用T3)
4.用小正方体搭成一个立体图形,画出从正面、上面、左面看到的形状。
正面
上面
左面
(教材P54 巩固应用T4)
5.两辆汽车从摄影师面前开过,摄影师依次拍摄了以下三幅照片。请你用序号标出摄影师的拍摄顺序。
①
②
③
(教材P54 巩固应用T5)
6.一根铁丝可以围成一个半径是3cm的圆,如果用它围成一个等边三角形,那么每边的长是多少厘米?
(教材P56 巩固应用T14)
2×3.14×3=18.84(cm)
18.84÷3=6.28(cm)
答:每边的长是6.28厘米。
7.下面是一个数学兴趣小组用一根长20dm的铁丝围图形的情况记录。
图形 周长/dm 长/dm 宽/dm 面积/dm2
长 方 形 20 9 1 9
20 8 2 16
20 7 3 21
20 6 4 24
20 5 5 25
圆 20 约31.85
(教材P56 巩固应用T15)
(1)分析以上实验记录,你发现了什么?
在周长相等的情况下,圆的面积大于长方形的面积。
(2)用上面的发现解释为什么排水管的
横截面都是圆形的。
所有材料相同的情况下,横截面是圆形,面积最大,排水最快。
8.求阴影部分的面积。
(教材P56 巩固应用T16)
(1)
梯形:(4+6)×4÷2= 20(cm2)
半圆:3.14×(4÷2)2÷2=6.28(cm2)
阴影部分:20-6.28=13.72(cm )
正方形:
20×20=400(cm2)
阴影部分:
400-314=86(cm2)
10cm
20cm
(2)
圆:
3.14×102=314(cm2)
9.银河广场有一个圆形喷水池,周长43.96m,有一条3m宽的小路围着喷水池,这条小路的面积是多少?
喷水池
小路
43.96÷3.14÷2 =7(m)
大圆的面积-小圆的面积=小路的面积
3.14×(7+3)2=314(m2)
3.14×72=153.86(m2)
314-153.86=160.14(m2)
答:这条小路的面积是160.14平方米。
3m
(教材P56 巩固应用T17)
情境导入
课堂小结
通过这节课的学习,你有什么收获
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
