第十一章三角形 同步练习(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十一章三角形 同步练习(含答案) 2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 08:11:44 | ||
图片预览




文档简介
第十一章三角形同步练习2024—2025学年人教版数学八年级上册
一、单选题
1.若一个多边形的内角和与外角和相等,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
2.和是一副三角板,,,,将这副三角板按如图所示的位置摆放,点在边上,点在边的延长线上,且,则( )
A. B. C. D.
3.现要用三根木棒搭一个三角形,已知其中两根木棒的长分别是3cm和5cm,那么第三根的长可以是( )
A.7cm B.8cm C.9cm D.10cm
4.如图,工人师傅砌门时,常用木条EF固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形具有稳定性
5.如图,中,点是和的平分线的交点,若,则( )
A. B. C. D.
6.如图,将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.150° B.120° C.165° D.135°
7.如果一个n边形的外角和是内角和的一半,那么n的值为( )
A.6 B.7 C.8 D.9
8.如图,在中,,,,若四边形的面积为,则的面积为( )
A.60 B.56 C.70 D.48
9.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
10.已知直线,,,射线的反向延长线交于点F,若,则m的值为( )
A.2.5 B.3 C.3.5 D.4
二、填空题
11.如图,在中,外角,,则的度数是 .
12.如果三角形的三条边长分别为,那么x的取值范围是 .
13.如果只用一种正多边形做平面密铺,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的每个内角度数为 .
14.在 中, , 、 分别是 的高线和角平分线, ,则 的度数为 .
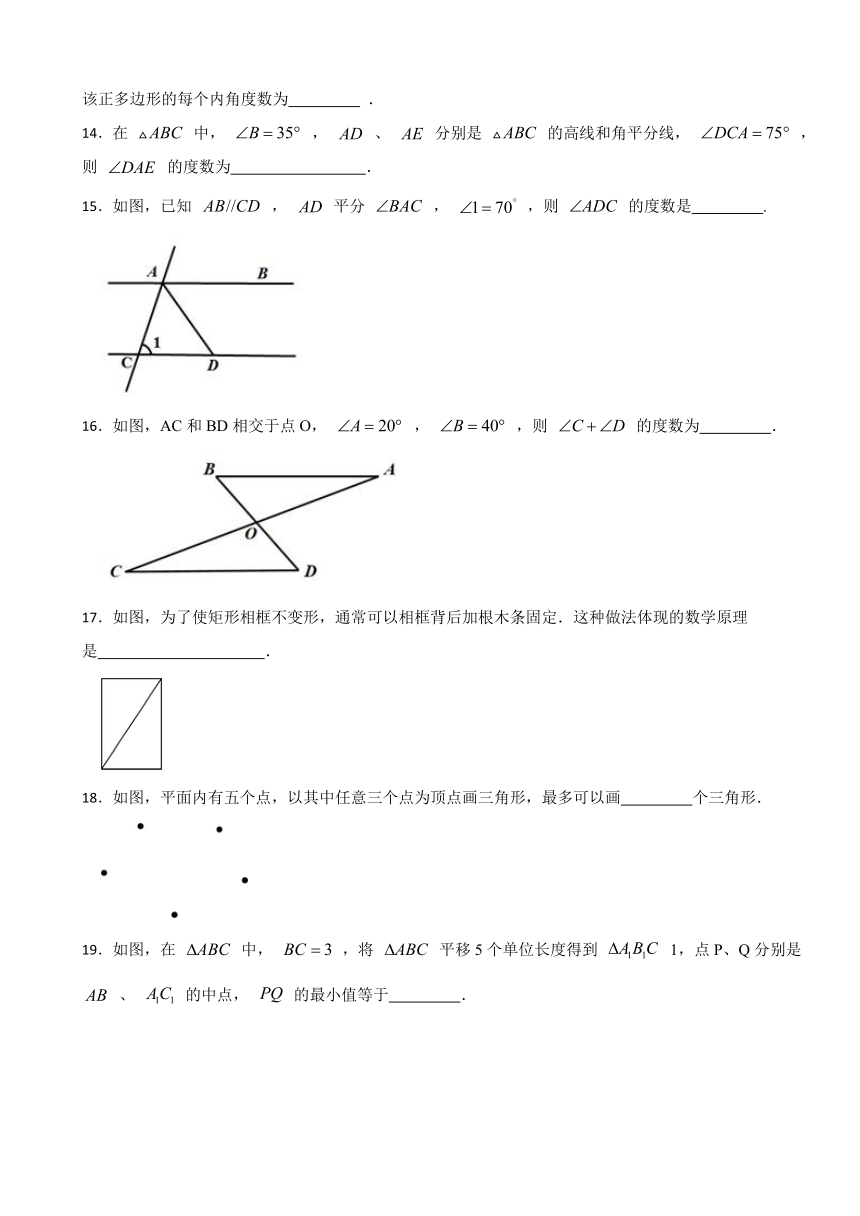
15.如图,已知 , 平分 , ,则 的度数是 .
16.如图,AC和BD相交于点O, , ,则 的度数为 .
17.如图,为了使矩形相框不变形,通常可以相框背后加根木条固定.这种做法体现的数学原理是 .
18.如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
19.如图,在 中, ,将 平移5个单位长度得到 1,点P、Q分别是 、 的中点, 的最小值等于 .
20.如图4,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
三、解答题
21.已知一个多边形的内角和与外角和相加等于,求这个多边形的边数及对角线的条数.
22.如图,在中, ,,的外角的平分线交的延长线于点E.求的度数.
23.已知:如图,在 中, , 于D, 平分 , ,求 的度数.
24.如图,在平面直角坐标系xOy中,已知点,,,且满足,是轴上一点,是线段上一点.
(1)求出点A,B,C的坐标;并直接写出与的位置关系;
(2)当点在线段上时,连接,,,探究,和的数量关系,并说明理由;
(3)若三角形的面积等于四边形的面积,直接写出点P的坐标.
25.如图,△ABC中,∠ABC的角平分线与外角∠ACD的平分线交于A1.
(1)如图1,若∠A=70°,则∠A1= .
(2)如图2,四边形ABCD中,∠ABC的角平分线及外角∠DCE的角平分线相交于点F, 若∠A+∠D=230°, 求∠F的度数.
(3)如图3,△ABC中,∠ABC的角平分线与外角∠ACD的角平分线交于A1,若E为BA延长线上一动点,连接EC,∠AEC与∠ACE的角平分线交于点Q ,当E滑动时有下面两个结论:
①∠Q+∠A1的值为定值;
②∠Q-∠A1的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
26.如图,已知,点C在上,点A、B在上.在中,,,点E、F在直线上,在中,,.
(1)图中的度数是多少;
(2)将沿直线平移,当点D在上时,求的度数;
(3)将沿直线平移,当以C、D、F为顶点的三角形中有两个角相等时,请直接写出的度数.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】
13.【答案】60°
14.【答案】 或
15.【答案】55°
16.【答案】60°
17.【答案】三角形具有稳定性
18.【答案】10
19.【答案】
20.【答案】52°
21.【答案】这个多边形的边数是12,它的对角线的条数是54.
22.【答案】解:中,,,
.
是的平分线,
23.【答案】解:在 中, ,
,
于D,
,
在 中, ,
平分 ,
,
.
24.【答案】(1)A,B,C,
(2)
(3)或
25.【答案】(1)35°
(2)解:如图:
∵BF平分∠ABC,CF平分∠DCE,
∴∠FBC=∠ABC,∠FCE=∠DCE
∴∠F=∠FCE-∠FBC=(∠DCE-∠ABC),
∵∠A+∠D=230°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=130°,
∴∠ABC+(180°-∠DCE)=130°,
∴∠DCE-∠ABC=50°,
∴∠F=(∠DCE-∠ABC)=25°;
(3)解:正确的结论是①,理由如下:
如图:
同(1)可得∠A1=∠BAC,
∵EQ平分∠AEC,CQ平分∠ACE,
∴∠QEC=∠AEC,∠QCE=∠ACE,
∵∠Q=180°-(∠QEC+∠QCE),
∴∠Q=180°-(∠AEC+∠ACE),
∵∠BAC=∠AEC+∠ACE,
∴∠Q=180°-∠BAC,
而∠A1=∠BAC,
∴∠Q+∠A1=180°-∠BAC+∠BAC=180°,
∴∠Q+∠A1的值为定值,①正确,其值是180°.
26.【答案】(1)解:∵,,,
∴,
∵,
∴;
(2)解:如图所示:
∵,,,
∴,
∵,
∴,
∵在中,,,
∴,
∵,
∴,
∵,
∴;
(3)解:∠CDE的度数为:60°或105°或15°或30°.
一、单选题
1.若一个多边形的内角和与外角和相等,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
2.和是一副三角板,,,,将这副三角板按如图所示的位置摆放,点在边上,点在边的延长线上,且,则( )
A. B. C. D.
3.现要用三根木棒搭一个三角形,已知其中两根木棒的长分别是3cm和5cm,那么第三根的长可以是( )
A.7cm B.8cm C.9cm D.10cm
4.如图,工人师傅砌门时,常用木条EF固定长方形门框,使其不变形,这样做的根据是( )
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形具有稳定性
5.如图,中,点是和的平分线的交点,若,则( )
A. B. C. D.
6.如图,将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.150° B.120° C.165° D.135°
7.如果一个n边形的外角和是内角和的一半,那么n的值为( )
A.6 B.7 C.8 D.9
8.如图,在中,,,,若四边形的面积为,则的面积为( )
A.60 B.56 C.70 D.48
9.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
10.已知直线,,,射线的反向延长线交于点F,若,则m的值为( )
A.2.5 B.3 C.3.5 D.4
二、填空题
11.如图,在中,外角,,则的度数是 .
12.如果三角形的三条边长分别为,那么x的取值范围是 .
13.如果只用一种正多边形做平面密铺,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的每个内角度数为 .
14.在 中, , 、 分别是 的高线和角平分线, ,则 的度数为 .
15.如图,已知 , 平分 , ,则 的度数是 .
16.如图,AC和BD相交于点O, , ,则 的度数为 .
17.如图,为了使矩形相框不变形,通常可以相框背后加根木条固定.这种做法体现的数学原理是 .
18.如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
19.如图,在 中, ,将 平移5个单位长度得到 1,点P、Q分别是 、 的中点, 的最小值等于 .
20.如图4,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
三、解答题
21.已知一个多边形的内角和与外角和相加等于,求这个多边形的边数及对角线的条数.
22.如图,在中, ,,的外角的平分线交的延长线于点E.求的度数.
23.已知:如图,在 中, , 于D, 平分 , ,求 的度数.
24.如图,在平面直角坐标系xOy中,已知点,,,且满足,是轴上一点,是线段上一点.
(1)求出点A,B,C的坐标;并直接写出与的位置关系;
(2)当点在线段上时,连接,,,探究,和的数量关系,并说明理由;
(3)若三角形的面积等于四边形的面积,直接写出点P的坐标.
25.如图,△ABC中,∠ABC的角平分线与外角∠ACD的平分线交于A1.
(1)如图1,若∠A=70°,则∠A1= .
(2)如图2,四边形ABCD中,∠ABC的角平分线及外角∠DCE的角平分线相交于点F, 若∠A+∠D=230°, 求∠F的度数.
(3)如图3,△ABC中,∠ABC的角平分线与外角∠ACD的角平分线交于A1,若E为BA延长线上一动点,连接EC,∠AEC与∠ACE的角平分线交于点Q ,当E滑动时有下面两个结论:
①∠Q+∠A1的值为定值;
②∠Q-∠A1的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
26.如图,已知,点C在上,点A、B在上.在中,,,点E、F在直线上,在中,,.
(1)图中的度数是多少;
(2)将沿直线平移,当点D在上时,求的度数;
(3)将沿直线平移,当以C、D、F为顶点的三角形中有两个角相等时,请直接写出的度数.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】
13.【答案】60°
14.【答案】 或
15.【答案】55°
16.【答案】60°
17.【答案】三角形具有稳定性
18.【答案】10
19.【答案】
20.【答案】52°
21.【答案】这个多边形的边数是12,它的对角线的条数是54.
22.【答案】解:中,,,
.
是的平分线,
23.【答案】解:在 中, ,
,
于D,
,
在 中, ,
平分 ,
,
.
24.【答案】(1)A,B,C,
(2)
(3)或
25.【答案】(1)35°
(2)解:如图:
∵BF平分∠ABC,CF平分∠DCE,
∴∠FBC=∠ABC,∠FCE=∠DCE
∴∠F=∠FCE-∠FBC=(∠DCE-∠ABC),
∵∠A+∠D=230°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=130°,
∴∠ABC+(180°-∠DCE)=130°,
∴∠DCE-∠ABC=50°,
∴∠F=(∠DCE-∠ABC)=25°;
(3)解:正确的结论是①,理由如下:
如图:
同(1)可得∠A1=∠BAC,
∵EQ平分∠AEC,CQ平分∠ACE,
∴∠QEC=∠AEC,∠QCE=∠ACE,
∵∠Q=180°-(∠QEC+∠QCE),
∴∠Q=180°-(∠AEC+∠ACE),
∵∠BAC=∠AEC+∠ACE,
∴∠Q=180°-∠BAC,
而∠A1=∠BAC,
∴∠Q+∠A1=180°-∠BAC+∠BAC=180°,
∴∠Q+∠A1的值为定值,①正确,其值是180°.
26.【答案】(1)解:∵,,,
∴,
∵,
∴;
(2)解:如图所示:
∵,,,
∴,
∵,
∴,
∵在中,,,
∴,
∵,
∴,
∵,
∴;
(3)解:∠CDE的度数为:60°或105°或15°或30°.
