第二十四章 圆 单元练习(含答案) 2024—2025学年人教版九年级数学上册
文档属性
| 名称 | 第二十四章 圆 单元练习(含答案) 2024—2025学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 907.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 08:14:18 | ||
图片预览



文档简介
第二十四章 圆 单元练习 2024—2025学年人教版九年级数学上册
一、单选题
1. 的半径 ,点P与圆心O的距离 ,则点P与 的位置关系是( )
A.点 在 外 B.点 在 上
C.点 在 内 D.不确定
2.牛顿曾说过: “反证法是数学家最精当的武器之一.” 那么我们用反证法证明命题 “等腰三角形的底角是锐角" 时, 第一步应假设( )
A.等腰三角形的底角是直角或钝角
B.等腰三角形的底角是直角
C.等腰三角形的底角是钝角
D.等腰三角形的底角是锐角
3.如图,是的两条直径,是劣弧的中点,连接,若,则的度数为( )
A. B. C. D.
4.如图,四边形 内接于 , 为 延长线上一点,若 ,则 的度数为( )
A. B. C. D.
5.如图,AB是中的一条弦,半径于点,交于点D,点是上一点,若,则( )
A. B. C. D.
6.如图,AB是的直径,弦,垂足为.连结OC,DB.如果,图中阴影部分的面积是,那么图中阴影部分的弧长是( )
A. B. C. D.
7.图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A.3 B.4 C.5 D.3.5
8.下列作图语句错误的有( )
①以点为圆心作弧;②延长射线OM到点;③延长线段AB到,使;④过三点A,B,作直线.
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
10.如图,正方形中,E是上一点, 将沿翻折得,点A的对应点是点F,直线与交于点H,与的平分线交于点G,连接,下列说法:①;②;③若连接,则;④若正方形边长为2,E为的中点,则.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,是的直径,是的内接三角形.若,,则的直径 .
12.如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为 .
13.已知⊙O的最大弦长为8cm,点A,B,C与圆心O的距离分别为2 cm,4 cm,6cm,则点A在圆 ,点B在圆 ,在圆 。
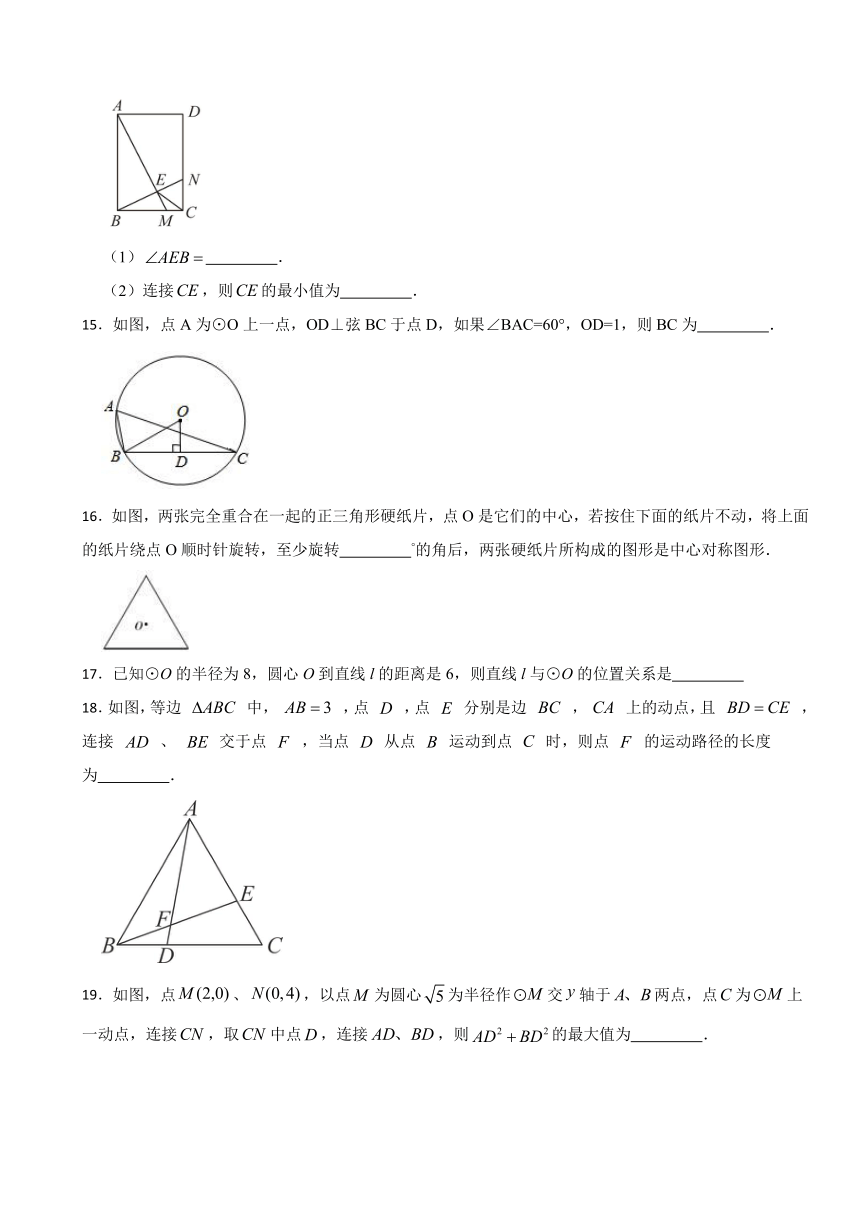
14.如图,在矩形中,,,M,N分别是,上的动点,连接,交于点E,且.
(1) .
(2)连接,则的最小值为 .
15.如图,点A为⊙O上一点,OD⊥弦BC于点D,如果∠BAC=60°,OD=1,则BC为 .
16.如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
17.已知⊙O的半径为8,圆心O到直线l的距离是6,则直线l与⊙O的位置关系是
18.如图,等边 中, ,点 ,点 分别是边 , 上的动点,且 ,连接 、 交于点 ,当点 从点 运动到点 时,则点 的运动路径的长度为 .
19.如图,点、,以点为圆心为半径作交轴于两点,点为上一动点,连接,取中点,连接,则的最大值为 .
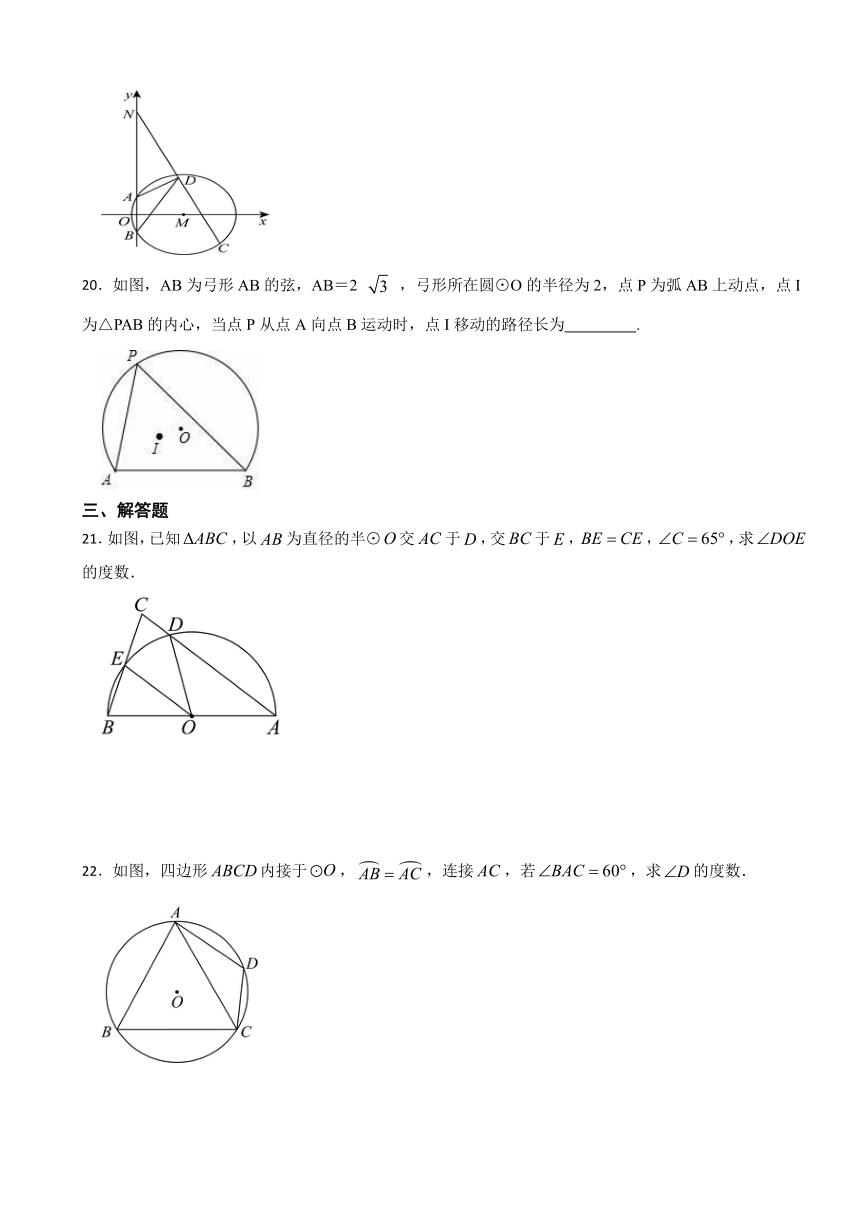
20.如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为 .
三、解答题
21.如图,已知,以为直径的半⊙交于,交于,,,求的度数.
22.如图,四边形内接于,,连接,若,求的度数.
23.如图中,,平分交于,以为圆心,为半径作交于.
(1) 求证:与相切;
(2)若,,试求的长.
24.在平面直角坐标系中,对于两点和直线,过点作直线的垂线,垂足为点,若点关于点的对称点为点,则称点为点关于直线和点的“垂足对称关联点”.已知点.
(1)①点关于轴和点的“垂足对称关联点”的坐标为______;
②点为点关于直线和点的“垂足对称关联点”,则点到直线的距离为______;
(2)如图,点在线段上,点在轴下方,且满足,若直线上存在点关于轴和点的“垂足对称关联点”,求的取值范围.
25.如图,PA为⊙O的切线,A为切点,过A作AB⊥OP,垂足为C,交⊙O于点B,延长BO与PA的延长线交于点D.
(1)求证:PB为⊙O的切线;
(2)若OB=3,OD=5,求AB的长.
26.在平面直角坐标系中,的半径为2,对于点和的弦,给出如下定义:若,则称弦是点的“关联弦”.
(1)如图1,已知点,点,,,,,,在弦,,中,点的“关联弦”是 ;
(2)如图2,已知点,在上,弦是点的“关联弦”,直接写出长度的最大值;
(3)如图3,已知点,,对于线段上一点,存在的弦,使得弦是点的“关联弦”,若对于每一个点,将其对应的“关联弦”长度的最大值记为,则当点在线段上运动时,直接写出的取值范围.
27.如图,在,,的平分线交于点,过点作直线的垂线交于点,是的外接圆.
(1)求证:是的切线;
(2)过点作于点,求证:平分;
(3)求证:.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】120°
13.【答案】内;上;外
14.【答案】(1)90°
(2)2
15.【答案】
16.【答案】60
17.【答案】相交
18.【答案】
19.【答案】
20.【答案】
21.【答案】
22.【答案】120度
23.【答案】(1)证明:过作于,
,
,
平分交于点,
,
与相切;
(2)解:设圆的半径为,
,,,
,
,是圆的切线,
,
,
,
,
在Rt中,,
解得:,
24.【答案】(1)①;②1
(2)
25.【答案】(1)证明:连接OA,
∵AB⊥OP,OB=OA,
∴∠BOP=∠AOP,
∵PA是⊙O的切线,
∴∠OAP=90°,
在△OBP与△OAP中,
,
∴△OBP≌△OAP(SAS),
∴∠OBP=∠OAP=90°,
∴OB⊥PB,
∴PB是⊙O的切线;
(2)解:∵OD=5,OA=OB=3,
∴在Rt△AOD中,AD==4,
∵PA、PB为⊙O的切线,
∴PA=PB,
在Rt△DBP中,PD2=PB2+BD2,即(PB+4)2=PB2+82,
∴PB=6,
在Rt△OBP中,OP===3,
∵S△BOP=OP BC=OB PB,
∴3BC=3×6,
∴BC=,
∴AB=2BC=.
26.【答案】(1),
(2)长度的最大值为
(3)
27.【答案】(1)证明:如图,连接.
,,
是圆的直径,
,
,
平分,
,,
,
,
是的切线
(2)证明:,,
,
是是直径,
,
,,
,
平分.
(3)证明:如图,连结.
是的平分线,于,于,
.
,,
,
,
,
,
一、单选题
1. 的半径 ,点P与圆心O的距离 ,则点P与 的位置关系是( )
A.点 在 外 B.点 在 上
C.点 在 内 D.不确定
2.牛顿曾说过: “反证法是数学家最精当的武器之一.” 那么我们用反证法证明命题 “等腰三角形的底角是锐角" 时, 第一步应假设( )
A.等腰三角形的底角是直角或钝角
B.等腰三角形的底角是直角
C.等腰三角形的底角是钝角
D.等腰三角形的底角是锐角
3.如图,是的两条直径,是劣弧的中点,连接,若,则的度数为( )
A. B. C. D.
4.如图,四边形 内接于 , 为 延长线上一点,若 ,则 的度数为( )
A. B. C. D.
5.如图,AB是中的一条弦,半径于点,交于点D,点是上一点,若,则( )
A. B. C. D.
6.如图,AB是的直径,弦,垂足为.连结OC,DB.如果,图中阴影部分的面积是,那么图中阴影部分的弧长是( )
A. B. C. D.
7.图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A.3 B.4 C.5 D.3.5
8.下列作图语句错误的有( )
①以点为圆心作弧;②延长射线OM到点;③延长线段AB到,使;④过三点A,B,作直线.
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
10.如图,正方形中,E是上一点, 将沿翻折得,点A的对应点是点F,直线与交于点H,与的平分线交于点G,连接,下列说法:①;②;③若连接,则;④若正方形边长为2,E为的中点,则.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,是的直径,是的内接三角形.若,,则的直径 .
12.如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为 .
13.已知⊙O的最大弦长为8cm,点A,B,C与圆心O的距离分别为2 cm,4 cm,6cm,则点A在圆 ,点B在圆 ,在圆 。
14.如图,在矩形中,,,M,N分别是,上的动点,连接,交于点E,且.
(1) .
(2)连接,则的最小值为 .
15.如图,点A为⊙O上一点,OD⊥弦BC于点D,如果∠BAC=60°,OD=1,则BC为 .
16.如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
17.已知⊙O的半径为8,圆心O到直线l的距离是6,则直线l与⊙O的位置关系是
18.如图,等边 中, ,点 ,点 分别是边 , 上的动点,且 ,连接 、 交于点 ,当点 从点 运动到点 时,则点 的运动路径的长度为 .
19.如图,点、,以点为圆心为半径作交轴于两点,点为上一动点,连接,取中点,连接,则的最大值为 .
20.如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为 .
三、解答题
21.如图,已知,以为直径的半⊙交于,交于,,,求的度数.
22.如图,四边形内接于,,连接,若,求的度数.
23.如图中,,平分交于,以为圆心,为半径作交于.
(1) 求证:与相切;
(2)若,,试求的长.
24.在平面直角坐标系中,对于两点和直线,过点作直线的垂线,垂足为点,若点关于点的对称点为点,则称点为点关于直线和点的“垂足对称关联点”.已知点.
(1)①点关于轴和点的“垂足对称关联点”的坐标为______;
②点为点关于直线和点的“垂足对称关联点”,则点到直线的距离为______;
(2)如图,点在线段上,点在轴下方,且满足,若直线上存在点关于轴和点的“垂足对称关联点”,求的取值范围.
25.如图,PA为⊙O的切线,A为切点,过A作AB⊥OP,垂足为C,交⊙O于点B,延长BO与PA的延长线交于点D.
(1)求证:PB为⊙O的切线;
(2)若OB=3,OD=5,求AB的长.
26.在平面直角坐标系中,的半径为2,对于点和的弦,给出如下定义:若,则称弦是点的“关联弦”.
(1)如图1,已知点,点,,,,,,在弦,,中,点的“关联弦”是 ;
(2)如图2,已知点,在上,弦是点的“关联弦”,直接写出长度的最大值;
(3)如图3,已知点,,对于线段上一点,存在的弦,使得弦是点的“关联弦”,若对于每一个点,将其对应的“关联弦”长度的最大值记为,则当点在线段上运动时,直接写出的取值范围.
27.如图,在,,的平分线交于点,过点作直线的垂线交于点,是的外接圆.
(1)求证:是的切线;
(2)过点作于点,求证:平分;
(3)求证:.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】120°
13.【答案】内;上;外
14.【答案】(1)90°
(2)2
15.【答案】
16.【答案】60
17.【答案】相交
18.【答案】
19.【答案】
20.【答案】
21.【答案】
22.【答案】120度
23.【答案】(1)证明:过作于,
,
,
平分交于点,
,
与相切;
(2)解:设圆的半径为,
,,,
,
,是圆的切线,
,
,
,
,
在Rt中,,
解得:,
24.【答案】(1)①;②1
(2)
25.【答案】(1)证明:连接OA,
∵AB⊥OP,OB=OA,
∴∠BOP=∠AOP,
∵PA是⊙O的切线,
∴∠OAP=90°,
在△OBP与△OAP中,
,
∴△OBP≌△OAP(SAS),
∴∠OBP=∠OAP=90°,
∴OB⊥PB,
∴PB是⊙O的切线;
(2)解:∵OD=5,OA=OB=3,
∴在Rt△AOD中,AD==4,
∵PA、PB为⊙O的切线,
∴PA=PB,
在Rt△DBP中,PD2=PB2+BD2,即(PB+4)2=PB2+82,
∴PB=6,
在Rt△OBP中,OP===3,
∵S△BOP=OP BC=OB PB,
∴3BC=3×6,
∴BC=,
∴AB=2BC=.
26.【答案】(1),
(2)长度的最大值为
(3)
27.【答案】(1)证明:如图,连接.
,,
是圆的直径,
,
,
平分,
,,
,
,
是的切线
(2)证明:,,
,
是是直径,
,
,,
,
平分.
(3)证明:如图,连结.
是的平分线,于,于,
.
,,
,
,
,
,
同课章节目录
