12.1全等三角形同步巩固练(含解析)2024--2025学年初中数学人教版八年级上册
文档属性
| 名称 | 12.1全等三角形同步巩固练(含解析)2024--2025学年初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 459.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-30 21:51:13 | ||
图片预览


文档简介
12.1 全等三角形 同步巩固练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.下列各组中是全等形的是( )
A.两个周长相等的等腰三角形 B.两个面积相等的长方形
C.两个面积相等的直角三角形 D.两个周长相等的圆
2.下列说法中,正确的是( )
A.全等图形是形状相同的两个图形
B.全等三角形是指面积相同的两个三角形
C.等边三角形都是全等三角形
D.全等图形的周长、面积都相等
3.已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
4.如图,若,则下列结论中不一定成立的是( )
A. B.
C. D.
5.如图,已知,,,则的长是( )
A. B. C. D.
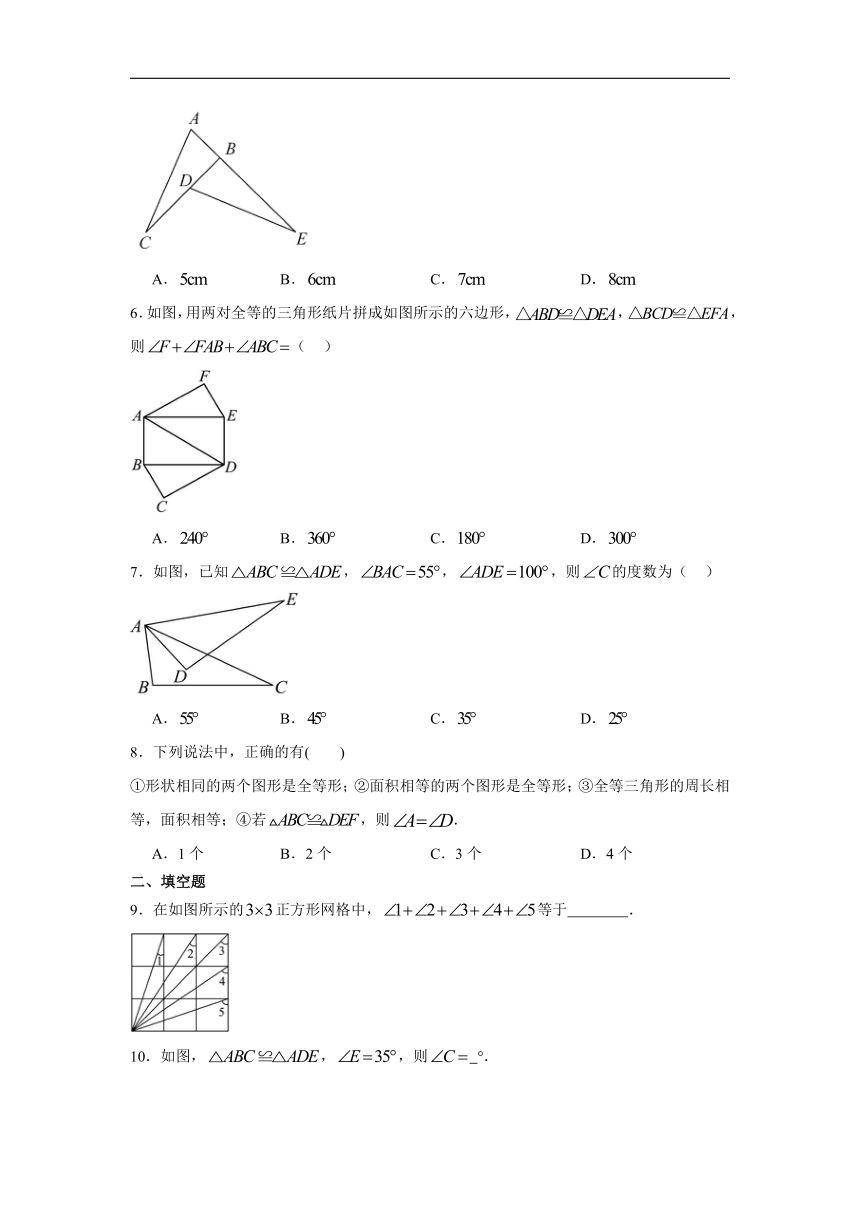
6.如图,用两对全等的三角形纸片拼成如图所示的六边形,,,则( )
A. B. C. D.
7.如图,已知,,,则的度数为( )
A. B. C. D.
8.下列说法中,正确的有( )
①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若,则.
A.1个 B.2个 C.3个 D.4个
二、填空题
9.在如图所示的正方形网格中,等于 .
10.如图,,,则 °.
11.如图,,若,则BD的长为 .
12.如图,,点在同一条直线上,,则的长为 .
13.已知,若的面积为,则的面积为 ;若的周长为,则的周长为 .
14.如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④ABDC.其中成立的是 .(填上序号即可)
三、解答题
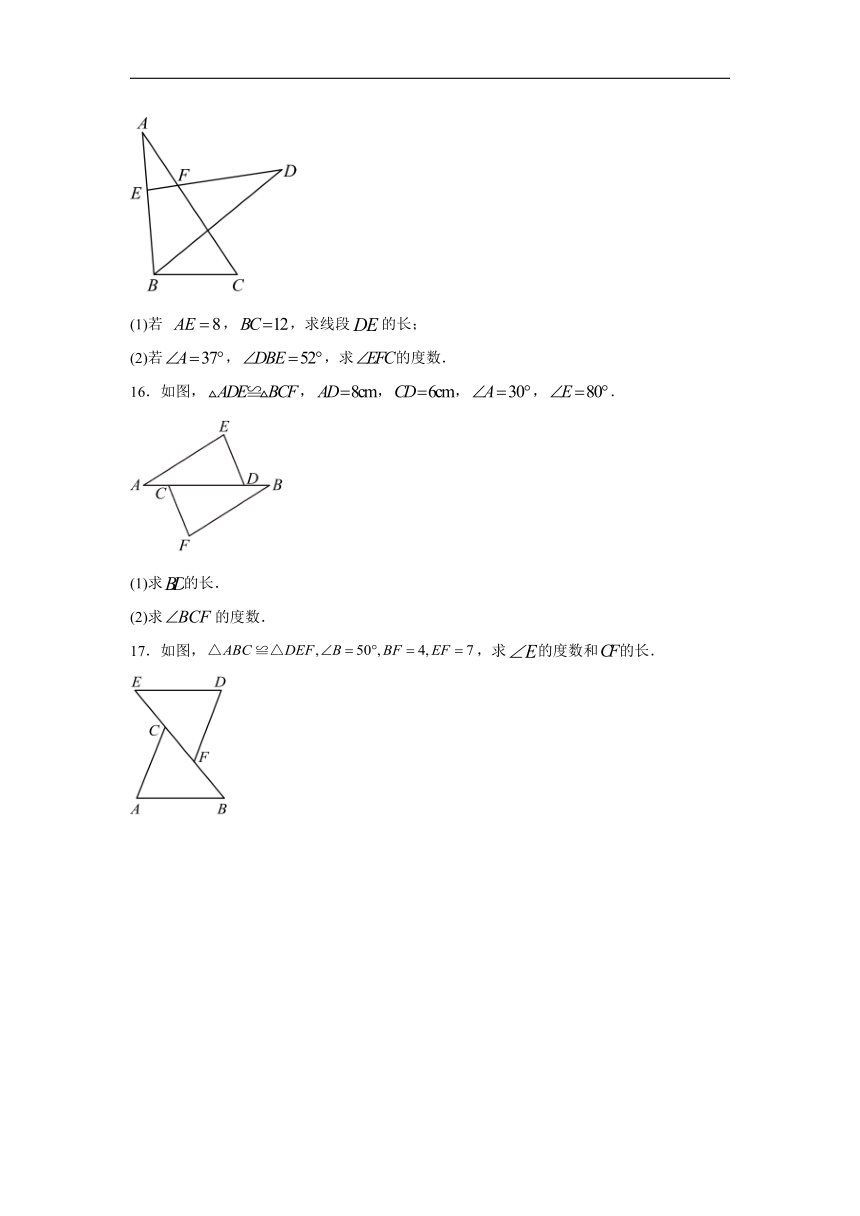
15.如图,已知,点E在边上,与交于点F.
(1)若 ,,求线段的长;
(2)若,,求的度数.
16.如图,,,,,.
(1)求的长.
(2)求的度数.
17.如图,,求的度数和的长.
参考答案:
1.D
A、不一定是全等形,故此选项错误;
B、不一定是全等形,故此选项错误;
C、不一定是全等形,故此选项错误;
D、是全等形,故此选项正确;
2.D
解:A.全等图形是指形状相同、大小相等的两个图形,故本选项错误;
B.全等三角形是指能够完全重合的两个三角形,故本选项错误;
C.等边三角形的形状相同、但是大小不一定相等,所以不一定都是全等三角形,故本选项错误;
D.全等图形的周长、面积相等,故本选项正确;
3.D
解:第一个三角形中、之间的夹角为,
是、之间的夹角,
两个三角形全等,
,
4.D
、∵,
∴,原选项成立,不符合题意;
、∵,
∴,原选项成立,不符合题意;
、∵,
∴,
∴,
∴,原选项成立,不符合题意;
、∵,
∴,原选项不一定成立,符合题意;
5.B
解:∵,
∴cm,cm,
即cm,
6.B
解:∵,,
∴,
∴
,
7.D
∵,
,
在中,,,
.
8.B
解:能够完全重合的两个图形叫做全等形,即形状和大小相同的两个图形是全等形,故①②说法错误;
全等三角形能够完全重合,所以全等三角形的周长相等,面积相等,故③说法正确;
若,的对应角为,所以,故④说法正确;
说法正确的有③④,共2个.
9./225度
解:观察图形可知与所在的三角形全等,二角互余,与所在的三角形全等,二角互余,,
∴,,,
∴.
故答案为:.
10.
∵,
∴,
∵,
∴,
故答案为:.
11.
解:∵,,
∴,
∵,
∴,
故答案为:.
12.1
解:∵,
∴,
∵,
∴,
故答案为:1.
13.
解:∵,
∴与形状和大小一致,能重合,,
∴它们的面积和周长相等,
∴若的面积为,则的面积为;
若的周长为,则的周长为.
故答案为:;.
14.①②③④
解:∵Rt△ABE≌Rt△ECD,
∴AE=ED,①成立;
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠D,
∵∠DEC+∠D=90°,
∴∠DEC+∠AEB=90°,
∴∠AED=90°,
∴AE⊥DE,②成立;
∵Rt△ABE≌Rt△ECD,
∴AB=EC,BE=CD,
∵BC=BE+EC,
∴BC=AB+CD,③成立;
∵∠B+∠C=180°,
∴AB∥DC,④成立,
故答案为:①②③④.
15.(1)20
(2)
(1)解:,
,,
,
;
(2)解:,
,
,,
,
.
16.(1)
(2)
(1)解:,,
,
又,
;
(2),,,
,,
.
17..
解:,
,
,
,
.
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.下列各组中是全等形的是( )
A.两个周长相等的等腰三角形 B.两个面积相等的长方形
C.两个面积相等的直角三角形 D.两个周长相等的圆
2.下列说法中,正确的是( )
A.全等图形是形状相同的两个图形
B.全等三角形是指面积相同的两个三角形
C.等边三角形都是全等三角形
D.全等图形的周长、面积都相等
3.已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
4.如图,若,则下列结论中不一定成立的是( )
A. B.
C. D.
5.如图,已知,,,则的长是( )
A. B. C. D.
6.如图,用两对全等的三角形纸片拼成如图所示的六边形,,,则( )
A. B. C. D.
7.如图,已知,,,则的度数为( )
A. B. C. D.
8.下列说法中,正确的有( )
①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若,则.
A.1个 B.2个 C.3个 D.4个
二、填空题
9.在如图所示的正方形网格中,等于 .
10.如图,,,则 °.
11.如图,,若,则BD的长为 .
12.如图,,点在同一条直线上,,则的长为 .
13.已知,若的面积为,则的面积为 ;若的周长为,则的周长为 .
14.如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④ABDC.其中成立的是 .(填上序号即可)
三、解答题
15.如图,已知,点E在边上,与交于点F.
(1)若 ,,求线段的长;
(2)若,,求的度数.
16.如图,,,,,.
(1)求的长.
(2)求的度数.
17.如图,,求的度数和的长.
参考答案:
1.D
A、不一定是全等形,故此选项错误;
B、不一定是全等形,故此选项错误;
C、不一定是全等形,故此选项错误;
D、是全等形,故此选项正确;
2.D
解:A.全等图形是指形状相同、大小相等的两个图形,故本选项错误;
B.全等三角形是指能够完全重合的两个三角形,故本选项错误;
C.等边三角形的形状相同、但是大小不一定相等,所以不一定都是全等三角形,故本选项错误;
D.全等图形的周长、面积相等,故本选项正确;
3.D
解:第一个三角形中、之间的夹角为,
是、之间的夹角,
两个三角形全等,
,
4.D
、∵,
∴,原选项成立,不符合题意;
、∵,
∴,原选项成立,不符合题意;
、∵,
∴,
∴,
∴,原选项成立,不符合题意;
、∵,
∴,原选项不一定成立,符合题意;
5.B
解:∵,
∴cm,cm,
即cm,
6.B
解:∵,,
∴,
∴
,
7.D
∵,
,
在中,,,
.
8.B
解:能够完全重合的两个图形叫做全等形,即形状和大小相同的两个图形是全等形,故①②说法错误;
全等三角形能够完全重合,所以全等三角形的周长相等,面积相等,故③说法正确;
若,的对应角为,所以,故④说法正确;
说法正确的有③④,共2个.
9./225度
解:观察图形可知与所在的三角形全等,二角互余,与所在的三角形全等,二角互余,,
∴,,,
∴.
故答案为:.
10.
∵,
∴,
∵,
∴,
故答案为:.
11.
解:∵,,
∴,
∵,
∴,
故答案为:.
12.1
解:∵,
∴,
∵,
∴,
故答案为:1.
13.
解:∵,
∴与形状和大小一致,能重合,,
∴它们的面积和周长相等,
∴若的面积为,则的面积为;
若的周长为,则的周长为.
故答案为:;.
14.①②③④
解:∵Rt△ABE≌Rt△ECD,
∴AE=ED,①成立;
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠D,
∵∠DEC+∠D=90°,
∴∠DEC+∠AEB=90°,
∴∠AED=90°,
∴AE⊥DE,②成立;
∵Rt△ABE≌Rt△ECD,
∴AB=EC,BE=CD,
∵BC=BE+EC,
∴BC=AB+CD,③成立;
∵∠B+∠C=180°,
∴AB∥DC,④成立,
故答案为:①②③④.
15.(1)20
(2)
(1)解:,
,,
,
;
(2)解:,
,
,,
,
.
16.(1)
(2)
(1)解:,,
,
又,
;
(2),,,
,,
.
17..
解:,
,
,
,
.
