第四单元多边形的面积(单元测试)-2024-2025学年小学数学五年级上册北师大版(含解析)
文档属性
| 名称 | 第四单元多边形的面积(单元测试)-2024-2025学年小学数学五年级上册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 219.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 10:23:52 | ||
图片预览




文档简介
第四单元多边形的面积(讲义)-2024-2025学年小学数学五年级上册北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个三角形的底是3cm,高是0.8cm,和它等底等高的平行四边形面积是( )cm2。
A.2.4 B.1.2 C.24 D.4.8
2.在下图中,平行四边形的面积是20平方厘米,图中阴影部分的面积是( )平方厘米。
A.2 B.4 C.8
3.如图,已知梯形的面积是72cm2,高是8cm,涂色面积是( )cm2。
A.48 B.24 C.12 D.6
4.一个等腰梯形,下底的长是上底的2倍,梯形中正方形的面积是1平方分米,这个梯形的面积是多少平方分米?( )
A.3平方分米 B.2平方分米 C.1.5平方分米
5.把一个三角形底扩大到原来的2倍,高扩大到原来的4倍,面积会扩大到原来的( )倍。
A.6 B.8 C.2
6.下面的图形中,有( )个是由两个相同的拼成的。
A.4 B.3 C.2 D.1
二、填空题
7.用字母表示梯形的面积公式是( );当它的上底和下底相等时, 梯形变成了( )形,这时的面积公式就是( );当它的上底是0时,梯形就变成了( )形,这时它的面积公式就是( ).
8.“转化”是一种重要的数学思想方法,在学习中经常用到。例如,在探究梯形面积计算公式时,可以将梯形沿两腰中点的连线剪开,将上面部分旋转后与下面部分拼成一个平行四边形,如下图。平行四边形的底等于梯形的( ),平行四边形的高等于梯形的( ),从而根据平行四边形的面积计算公式推导出梯形的面积计算公式。请你再举一个学习数学知识时应用“转化”方法的例子:( )。
9.一个平行四边形的面积是,底边长是,高是( )。
10.填空
上图中的平行四边形是沿着( )剪开的,通过平移,可以拼成一个( ),它的长就是原来平行四边形的( ),它的宽就是原来平行四边形的( ).它的面积与原来平行四边形的面积( ).
11.一个三角形原来的底是14cm,如果将底增加2cm,面积就增加2cm2。原来三角形的面积是( )cm2。
12.一个三角形的面积是56平方厘米,它的一条底边长是7厘米,这条底边上的高是( )。
13.下图直角三形的面积是( )平方厘米,斜边上的高是( )厘米。
14.下图中长方形的面积是24cm ,那么阴影部分的面积是( )cm 。
15.一个平行四边形的面积是26平方厘米,和它等底等高的三角形面积是( )平方厘米。
三、判断题
16.梯形的高不变,上底和下底都扩大到原来的2倍,面积就扩大到原来的4倍。( )
17.平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。( )
18.梯形有无数条高,并且每条高的长度都相等.( )
19.一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是12厘米,则三角形的底是6厘米。( )
20.两个三角形的底和高相等,它们的面积相等,形状也相同。( )
21.当梯形的上下底位置一定时,梯形的高随两条侧边变化。( )
四、计算题
22.求下列图形的面积.
23.看图列方程,并求出方程的解。(平行四边形的面积是16.2m2。)
五、作图题
24.在平行线间分别画出一个面积相等的锐角三角形、直角三角形和钝角三角形。
六、解答题
25.一个锐角三角形的三条边的长度都是两位数,而且是三个连续偶数,它们个位数字的和是7的倍数.这个三角形的周长最长应该是多少厘米?
26.李爷爷开垦了一块梯形菜地,上底是15米,下底是40米,高是18米,如果每平方米可收入48.5元,这块地可收入多少元?
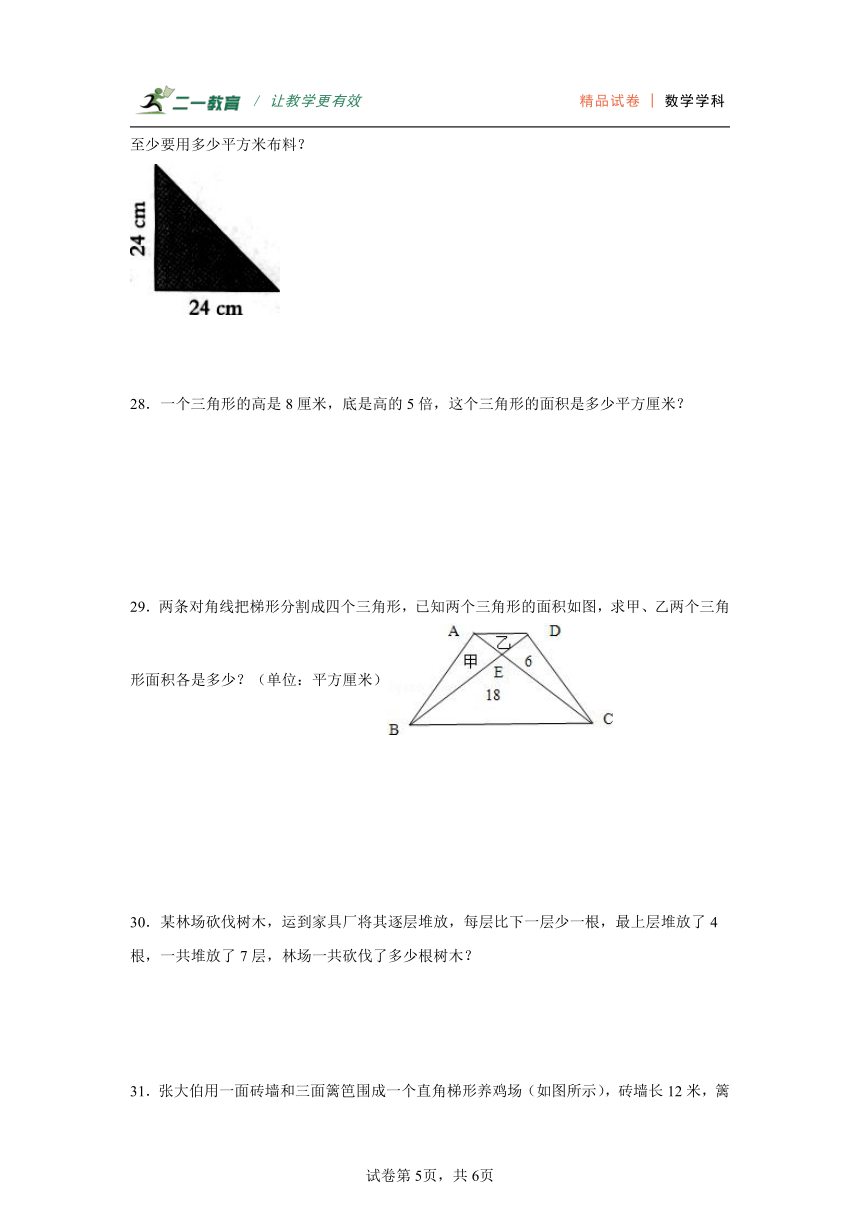
27.一种直角三角形的小旗(如下图),两条直角边的长度都是24cm,做150面这样的小旗,至少要用多少平方米布料?
28.一个三角形的高是8厘米,底是高的5倍,这个三角形的面积是多少平方厘米?
29.两条对角线把梯形分割成四个三角形,已知两个三角形的面积如图,求甲、乙两个三角形面积各是多少?(单位:平方厘米)
30.某林场砍伐树木,运到家具厂将其逐层堆放,每层比下一层少一根,最上层堆放了4根,一共堆放了7层,林场一共砍伐了多少根树木?
31.张大伯用一面砖墙和三面篱笆围成一个直角梯形养鸡场(如图所示),砖墙长12米,篱笆总长60米。这个鸡场的面积大约是多少平方米?
32.一块长方形平面钢板的长是1.5米,高是0.8米,从这块钢板上截下一块底长4分米,高5分米的三角形钢板,剩下钢板的面积是多少平方米?
33.永兴村村民集资修一条长5千米的水渠,渠面宽1.2米,渠底宽0.8米,渠高0.5米,计划20天挖完,平均每天挖土多少立方米?
34.一片水田(如图),有一条2m宽的灌溉水道从中穿过,求水田的面积.(单位:m)
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由于三角形的底和高跟平行四边形的底和高相同,根据平行四边形的面积公式,底×高,把数代入公式即可求解。
【详解】3×0.8=2.4(平方厘米)
故答案为:A。
【点睛】本题主要考查平行四边形的面积公式,熟练掌握平行四边形的面积公式并灵活运用。
2.B
【分析】根据图形可知,平行四边形的底边是2+3=5厘米,平行四边形的面积是20平方厘米,根据平行四边形的面积公式:底×高,求出平行四边形的高,阴影部分三角形的高等于平行四边形的高,阴影部分三角形的底是2,根据三角形面积公式:底×高÷2,即可解答。
【详解】2×[20÷(2+3)]÷2
=2×[20÷5]÷2
=2×4÷2
=8÷2
=4(平方厘米)
故答案选:B
【点睛】本题考查平行四边形面积公式、三角形面积公式的应用,熟记公式,灵活运用。
3.A
【分析】由图可知,梯形被分成了三个面积相等的三角形,涂色面积为2个三角形的面积。据此解答。
【详解】72÷3×2=48(cm2)
梯形的面积是72cm2,高是8cm,涂色面积是48cm2。
故答案为:A
4.C
【分析】根据题意,可设梯形的上底为r分米,则下底为2r分米,然后再根据正方形的面积公式和梯形的面积公式进行计算即可得到梯形的面积。
【详解】梯形的上底为r分米,则下底为2r分米。
正方形的面积为:r2=1
梯形的面积为:
(r+2r)r÷2
=3r2÷2
=3×1÷2
=3÷2
=1.5(平方分米)
故答案为:C
【点睛】此题主要考查的是梯形面积公式和正方形面积公式的灵活应用。
5.B
【分析】一个因数扩大(或缩小)几倍,另一个因数扩大(或缩小)几倍,积就扩大(或缩小)两个因数扩大(或缩小)倍数的乘积倍。
【详解】三角形的面积=底×高÷2,如果底扩大到原来的2倍,高扩大到原来的4倍,根据积的变化规律,可知面积扩大2×4=8倍。
故答案为:B
6.C
【解析】略
7. S=(a+b)h÷2 平行四边 S=ah 三角 S=ah÷2
【解析】略
8. 两底之和 高的一半 将平行四边形剪拼成长方形,推导平行四边形的面积公式
【分析】转化思想,就是将未知解法或难以解决的问题,通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为已知知识范围内已经解决或容易解决的问题方法的数学思想。
【详解】“转化”是一种重要的数学思想方法,在学习中经常用到。例如,在探究梯形面积计算公式时,可以将梯形沿两腰中点的连线剪开,将上面部分旋转后与下面部分拼成一个平行四边形,如下图。平行四边形的底等于梯形的两底之和,平行四边形的高等于梯形高的一半,从而根据平行四边形的面积计算公式推导出梯形的面积计算公式。请你再举一个学习数学知识时应用“转化”方法的例子:将平行四边形剪拼成长方形,推导平行四边形的面积公式。
9.8
【分析】平行四边形的面积=底×高,用面积除以底即可求出平行四边形的高。
【详解】72÷9=8(厘米)
【点睛】本题考查有关平行四边形面积的计算,根据面积公式即可解答。
10. 高 长方形 底 高 相等
【详解】略
11.14
【解析】略
12.16厘米
【分析】三角形高=面积×2÷底,据此代入数据计算即可。
【详解】56×2÷7
=112÷7
=16(厘米)
这条底边上的高是16厘米。
【点睛】此题考查了三角形面积的相关计算,求三角形的底或高时,需先让面积×2。
13. 6 2.4
【分析】根据三角形的面积=底×高÷2,高=三角形的面积×2÷底,代入数据计算即可。
【详解】4×3÷2=6(平方厘米),三角形的面积是6平方厘米。
6×2÷5=2.4(厘米),斜边上的高是2.4厘米。
【点睛】此题主要考查了三角形面积公式的灵活运用。明确在直角三角形中,两条直角边就是对应的底和高,斜边上的高等于两条直角边的积除以斜边。
14.12
【分析】长方形的面积=长×宽,三角形的面积=底×高÷2;图中长方形的长相当于三角形的底,长方形的宽相当于三角形的高,据此可知,阴影部分的面积等于长方形面积的一半;据此计算即可。
【详解】24÷2=12(平方厘米)
15.13
【分析】假定平行四边形的底是a,高是h,则面积是:a×h=26平方厘米;和它等底等高的三角形面积是:a×h÷2=26÷2=13平方厘米。据此解答。
【详解】假定平行四边形的底是a,高是h,则面积是:a×h=26(平方厘米)
和它等底等高的三角形面积是:a×h÷2=26÷2=13(平方厘米)
【点睛】掌握等底等高的三角形与平行四边形面积之间的关系是解答本题的关键。
16.×
【分析】梯形面积=(上底+下底)×高÷2,根据梯形面积公式可知:2是固定值,上底与下底的和,作为一个因数存在,另外一个因数是高,再根据积的变化规律:如果一个因数扩大若干倍,另一个因数不变,那么积也扩大相同倍数,进行判断即可。
【详解】由分析可得:
因为上底与下底的和,作为一个因数存在,高不变时,上底和下底同时扩大2倍,面积扩大到原来的2倍,原题说法错误。
故答案为:×
【点睛】本题考查了梯形面积公式和积的变化规律,需要学生熟练掌握积和因数之间的变化关系。
17.√
【详解】平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。
如图:
原题干说法正确。
故答案为:√
18.√
【分析】梯形的高是从上底的任意一点向下底做垂直线段,这个垂直线段就是梯形的高,梯形的上底和下底是平行的,所以从上底可以向下底做无数条垂直线段,因此梯形有无数条高。
【详解】梯形的上底和下底是平行的,两条平行线段之间有无数条垂直线段,梯形也就有无数条高。原题说法正确。
故答案为:√
【点睛】考查梯形特点的相关知识,重点是知道梯形的高有无数条。
19.×
【分析】分析题目,一个平行四边形和一个三角形面积相等,高也相等,则三角形的底是平行四边形底的2倍,据此解答。
【详解】12×2=24(厘米)
三角形的底是24厘米。
故答案为:×
【点睛】掌握面积和高都相等的三角形和平行四边形底之间的关系是解答本题的关键。
20.×
【分析】三角形的面积=底×高÷2,则当两个三角形的底和高相等,它们的面积也相等,但是它们的形状不一定相等,如下图所示,两个三角形底和高都相等,但它们的形状不同。
【详解】根据三角形的面积公式可知,两个三角形的底和高相等,它们的面积相等,但它们的形状不一定相同。原题说法错误。
故答案为:×
【点睛】掌握三角形的特征和面积公式是解题的关键。
21.×
【分析】只有一组对边平行的四边形叫做梯形。平行的两边叫做梯形的底边,较长的一条底边叫下底,较短的一条底边叫上底,另外两边叫腰。夹在两底之间的垂线段是梯形的高,梯形的高与上下底位置相关。
【详解】当梯形的上下底位置一定时,梯形的高与两条侧边变化无关。原题说法错误。
故答案为:×。
【点睛】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。梯形有2条底,有无数条高。
22.13.5 4.5 11.4
【详解】4.5×3=13.5() 3.6×2.5÷2=4.5() (2.4+3.6)×3.8÷2=11.4()
23.4.5m
【分析】平行四边形的高是m,根据等量关系:底×高=平行四边形的面积,列方程解答即可。
【详解】
解:
24.见详解
【分析】三角形的面积=底×高÷2,因为平行线间的距离处处相等,也就是三个三角形的高是相等,画出的锐角三角形、直角三角形和钝角三角形的底相等,那么这三个三角形的面积就相等。
【详解】如图所示:
【点睛】掌握三角形的面积计算公式是解题关键。
25.264厘米
【详解】试题分析:依题意,三个数的末位数字和能被7整除的只有7、14、21等三种.但三个两位的连续偶数相加其和也一定是偶数,故符合题意的只有14.所以三个最小的两位连续偶数它们的末位数字又能被7整除的,便是16、18、20,它们的和即三角形最小周长为16+18+20;这样三个最大的两位连续偶数.它们的末位数字又能被7整除的,便是90、88、86,它们的和即三角形最大周长为90+88+86.
解:依题意,因为三角形三边是三个连续偶数,所以它们的个位数字只能是0,2,4,6,8,并且它们的和也是偶数,
又因为它们的个位数字的和是7的倍数,所以只能是14,
三角形三条边最小应该是:16、18、20,
周长最小为:16+18+20=54(厘米),
三角形三条边最大应该是:86,88,90,
那么周长最长为86+88+90=264(厘米),
答:这个三角形的周长最长应该是264厘米.
点评:此题考查了三角形的特性以及被7整除的数的性质.
26.24007.5元
【分析】先利用梯形的面积公式求出菜地的面积,再乘每平方米收入的钱数,就是总收入,据此解答即可.
【详解】(15+40)×18÷2×48.5,
=55×18÷2×48.5,
=495×48.5,
=24007.5(元),
答:这块菜地一共收入24007.5元钱.
27.4.32
【详解】24×24÷2=288()=0.0288() 0.0288×150=4.32()
答:至少要用4.32布料.
28.160平方厘米
【详解】试题分析:先用“8×5”求出三角形的底的长度,然后根据“三角形的面积=底×高÷2”进行解答即可.
解:8×5=40(厘米),
40×8÷2,
=320÷2,
=160(平方厘米),
答:这个三角形的面积是160平方厘米.
点评:此题考查了三角形的面积公式,利用公式解答即可.
29.6平方厘米;2平方厘米
【详解】试题分析:因为在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,所以两个三角形的面积相等;进而得出甲的面积与三角形DEC的面积相等,即甲的面积是6平方厘米;再根据三角形的面积与底的关系得出BE:ED=18:6=3:1,由此即可求出乙的面积.
解:因为,在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,
所以,三角形ABD与三角形DAC的面积相等,
所以,甲的面积与三角形DEC的面积相等,
甲的面积是6平方厘米,
而,BE:ED=18:6=3:1,
甲的面积:乙的面积=3:1,
乙的面积是:6÷3=2(平方厘米),
答:甲的面积是6平方厘米;乙的面积是2平方厘米.
点评:解答此题的关键是,利用同底等高的性质与三角形的面积与底的关系,得出面积与面积的关系,及边长与面积的关系,从而得出答案.
30.49根
【详解】试题分析:根据堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据进行解答.
解:[4+(7﹣1+4)]×7÷2,
=[4+10]×7÷2,
=14×7÷2,
=49(根).
答:林场一共砍伐了49根树木.
点评:本题主要考查了学生对根数=(上层根数+下层根数)×层数÷2,这一数量关系的掌握情况.
31.264平方米
【分析】梯形的面积=(上底+下底)×高÷2,其中上、下底之和=篱笆总长米数-16,梯形的高就是砖墙长度,据此解答。
【详解】(60-16)×12÷2
=44×6
=264(平方米)
答:这个鸡场的面积大约是264平方米。
【点睛】此题考查了梯形的面积计算,找出梯形的上下底之和以及梯形的高是解题关键。
32.1.1平方米
【详解】试题分析:由题意可知:长方形的面积减去三角形的面积就是剩余的面积,将数据分别代入长方形和三角形的面积公式即可求解.
解:4分米=0.4米,5分米=0.5米,
1.5×0.8﹣0.4×0.5÷2,
=1.2﹣0.1,
=1.1(平方米);
答:剩下的面积是1.1平方米.
点评:此题主要考查长方形和三角形的面积计算方法.
33.125立方米
【详解】试题分析:先根据梯形的面积公式:S=(a+b)h÷2,求出这条水渠的横截面积,再根据V=sh,求出这条水渠挖出土的体积,再除以20,就是平均每天挖土的方数.据此解答.
解:5千米=5000米,
(1.2+0.8)×0.5÷2,
=2×0.5÷2,
=0.5(平方米),
0.5×5000÷20,
=2500÷20,
=125(立方米).
答:平均每天挖土125立方米.
点评:本题的关键是根据V=sh求出这条水渠挖出土的体积,然后再根据除法的意义解答.
34.1215平方米
【详解】试题分析:根据题意,可利用梯形的面积公式确定原来水田的面积,再利用平行四边形的面积公式计算出灌溉水道的面积,最后用原来水田的面积减去灌溉水道占用的面积即可.
解:(60+25)×30×﹣2×30,
=85×30×﹣2×30,
=1275﹣60,
=1215(平方米),
答:水田的面积是1215平方米.
点评:此题主要考查的是梯形的面积公式和平行四边形面积公式的灵活应用.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个三角形的底是3cm,高是0.8cm,和它等底等高的平行四边形面积是( )cm2。
A.2.4 B.1.2 C.24 D.4.8
2.在下图中,平行四边形的面积是20平方厘米,图中阴影部分的面积是( )平方厘米。
A.2 B.4 C.8
3.如图,已知梯形的面积是72cm2,高是8cm,涂色面积是( )cm2。
A.48 B.24 C.12 D.6
4.一个等腰梯形,下底的长是上底的2倍,梯形中正方形的面积是1平方分米,这个梯形的面积是多少平方分米?( )
A.3平方分米 B.2平方分米 C.1.5平方分米
5.把一个三角形底扩大到原来的2倍,高扩大到原来的4倍,面积会扩大到原来的( )倍。
A.6 B.8 C.2
6.下面的图形中,有( )个是由两个相同的拼成的。
A.4 B.3 C.2 D.1
二、填空题
7.用字母表示梯形的面积公式是( );当它的上底和下底相等时, 梯形变成了( )形,这时的面积公式就是( );当它的上底是0时,梯形就变成了( )形,这时它的面积公式就是( ).
8.“转化”是一种重要的数学思想方法,在学习中经常用到。例如,在探究梯形面积计算公式时,可以将梯形沿两腰中点的连线剪开,将上面部分旋转后与下面部分拼成一个平行四边形,如下图。平行四边形的底等于梯形的( ),平行四边形的高等于梯形的( ),从而根据平行四边形的面积计算公式推导出梯形的面积计算公式。请你再举一个学习数学知识时应用“转化”方法的例子:( )。
9.一个平行四边形的面积是,底边长是,高是( )。
10.填空
上图中的平行四边形是沿着( )剪开的,通过平移,可以拼成一个( ),它的长就是原来平行四边形的( ),它的宽就是原来平行四边形的( ).它的面积与原来平行四边形的面积( ).
11.一个三角形原来的底是14cm,如果将底增加2cm,面积就增加2cm2。原来三角形的面积是( )cm2。
12.一个三角形的面积是56平方厘米,它的一条底边长是7厘米,这条底边上的高是( )。
13.下图直角三形的面积是( )平方厘米,斜边上的高是( )厘米。
14.下图中长方形的面积是24cm ,那么阴影部分的面积是( )cm 。
15.一个平行四边形的面积是26平方厘米,和它等底等高的三角形面积是( )平方厘米。
三、判断题
16.梯形的高不变,上底和下底都扩大到原来的2倍,面积就扩大到原来的4倍。( )
17.平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。( )
18.梯形有无数条高,并且每条高的长度都相等.( )
19.一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是12厘米,则三角形的底是6厘米。( )
20.两个三角形的底和高相等,它们的面积相等,形状也相同。( )
21.当梯形的上下底位置一定时,梯形的高随两条侧边变化。( )
四、计算题
22.求下列图形的面积.
23.看图列方程,并求出方程的解。(平行四边形的面积是16.2m2。)
五、作图题
24.在平行线间分别画出一个面积相等的锐角三角形、直角三角形和钝角三角形。
六、解答题
25.一个锐角三角形的三条边的长度都是两位数,而且是三个连续偶数,它们个位数字的和是7的倍数.这个三角形的周长最长应该是多少厘米?
26.李爷爷开垦了一块梯形菜地,上底是15米,下底是40米,高是18米,如果每平方米可收入48.5元,这块地可收入多少元?
27.一种直角三角形的小旗(如下图),两条直角边的长度都是24cm,做150面这样的小旗,至少要用多少平方米布料?
28.一个三角形的高是8厘米,底是高的5倍,这个三角形的面积是多少平方厘米?
29.两条对角线把梯形分割成四个三角形,已知两个三角形的面积如图,求甲、乙两个三角形面积各是多少?(单位:平方厘米)
30.某林场砍伐树木,运到家具厂将其逐层堆放,每层比下一层少一根,最上层堆放了4根,一共堆放了7层,林场一共砍伐了多少根树木?
31.张大伯用一面砖墙和三面篱笆围成一个直角梯形养鸡场(如图所示),砖墙长12米,篱笆总长60米。这个鸡场的面积大约是多少平方米?
32.一块长方形平面钢板的长是1.5米,高是0.8米,从这块钢板上截下一块底长4分米,高5分米的三角形钢板,剩下钢板的面积是多少平方米?
33.永兴村村民集资修一条长5千米的水渠,渠面宽1.2米,渠底宽0.8米,渠高0.5米,计划20天挖完,平均每天挖土多少立方米?
34.一片水田(如图),有一条2m宽的灌溉水道从中穿过,求水田的面积.(单位:m)
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由于三角形的底和高跟平行四边形的底和高相同,根据平行四边形的面积公式,底×高,把数代入公式即可求解。
【详解】3×0.8=2.4(平方厘米)
故答案为:A。
【点睛】本题主要考查平行四边形的面积公式,熟练掌握平行四边形的面积公式并灵活运用。
2.B
【分析】根据图形可知,平行四边形的底边是2+3=5厘米,平行四边形的面积是20平方厘米,根据平行四边形的面积公式:底×高,求出平行四边形的高,阴影部分三角形的高等于平行四边形的高,阴影部分三角形的底是2,根据三角形面积公式:底×高÷2,即可解答。
【详解】2×[20÷(2+3)]÷2
=2×[20÷5]÷2
=2×4÷2
=8÷2
=4(平方厘米)
故答案选:B
【点睛】本题考查平行四边形面积公式、三角形面积公式的应用,熟记公式,灵活运用。
3.A
【分析】由图可知,梯形被分成了三个面积相等的三角形,涂色面积为2个三角形的面积。据此解答。
【详解】72÷3×2=48(cm2)
梯形的面积是72cm2,高是8cm,涂色面积是48cm2。
故答案为:A
4.C
【分析】根据题意,可设梯形的上底为r分米,则下底为2r分米,然后再根据正方形的面积公式和梯形的面积公式进行计算即可得到梯形的面积。
【详解】梯形的上底为r分米,则下底为2r分米。
正方形的面积为:r2=1
梯形的面积为:
(r+2r)r÷2
=3r2÷2
=3×1÷2
=3÷2
=1.5(平方分米)
故答案为:C
【点睛】此题主要考查的是梯形面积公式和正方形面积公式的灵活应用。
5.B
【分析】一个因数扩大(或缩小)几倍,另一个因数扩大(或缩小)几倍,积就扩大(或缩小)两个因数扩大(或缩小)倍数的乘积倍。
【详解】三角形的面积=底×高÷2,如果底扩大到原来的2倍,高扩大到原来的4倍,根据积的变化规律,可知面积扩大2×4=8倍。
故答案为:B
6.C
【解析】略
7. S=(a+b)h÷2 平行四边 S=ah 三角 S=ah÷2
【解析】略
8. 两底之和 高的一半 将平行四边形剪拼成长方形,推导平行四边形的面积公式
【分析】转化思想,就是将未知解法或难以解决的问题,通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为已知知识范围内已经解决或容易解决的问题方法的数学思想。
【详解】“转化”是一种重要的数学思想方法,在学习中经常用到。例如,在探究梯形面积计算公式时,可以将梯形沿两腰中点的连线剪开,将上面部分旋转后与下面部分拼成一个平行四边形,如下图。平行四边形的底等于梯形的两底之和,平行四边形的高等于梯形高的一半,从而根据平行四边形的面积计算公式推导出梯形的面积计算公式。请你再举一个学习数学知识时应用“转化”方法的例子:将平行四边形剪拼成长方形,推导平行四边形的面积公式。
9.8
【分析】平行四边形的面积=底×高,用面积除以底即可求出平行四边形的高。
【详解】72÷9=8(厘米)
【点睛】本题考查有关平行四边形面积的计算,根据面积公式即可解答。
10. 高 长方形 底 高 相等
【详解】略
11.14
【解析】略
12.16厘米
【分析】三角形高=面积×2÷底,据此代入数据计算即可。
【详解】56×2÷7
=112÷7
=16(厘米)
这条底边上的高是16厘米。
【点睛】此题考查了三角形面积的相关计算,求三角形的底或高时,需先让面积×2。
13. 6 2.4
【分析】根据三角形的面积=底×高÷2,高=三角形的面积×2÷底,代入数据计算即可。
【详解】4×3÷2=6(平方厘米),三角形的面积是6平方厘米。
6×2÷5=2.4(厘米),斜边上的高是2.4厘米。
【点睛】此题主要考查了三角形面积公式的灵活运用。明确在直角三角形中,两条直角边就是对应的底和高,斜边上的高等于两条直角边的积除以斜边。
14.12
【分析】长方形的面积=长×宽,三角形的面积=底×高÷2;图中长方形的长相当于三角形的底,长方形的宽相当于三角形的高,据此可知,阴影部分的面积等于长方形面积的一半;据此计算即可。
【详解】24÷2=12(平方厘米)
15.13
【分析】假定平行四边形的底是a,高是h,则面积是:a×h=26平方厘米;和它等底等高的三角形面积是:a×h÷2=26÷2=13平方厘米。据此解答。
【详解】假定平行四边形的底是a,高是h,则面积是:a×h=26(平方厘米)
和它等底等高的三角形面积是:a×h÷2=26÷2=13(平方厘米)
【点睛】掌握等底等高的三角形与平行四边形面积之间的关系是解答本题的关键。
16.×
【分析】梯形面积=(上底+下底)×高÷2,根据梯形面积公式可知:2是固定值,上底与下底的和,作为一个因数存在,另外一个因数是高,再根据积的变化规律:如果一个因数扩大若干倍,另一个因数不变,那么积也扩大相同倍数,进行判断即可。
【详解】由分析可得:
因为上底与下底的和,作为一个因数存在,高不变时,上底和下底同时扩大2倍,面积扩大到原来的2倍,原题说法错误。
故答案为:×
【点睛】本题考查了梯形面积公式和积的变化规律,需要学生熟练掌握积和因数之间的变化关系。
17.√
【详解】平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。
如图:
原题干说法正确。
故答案为:√
18.√
【分析】梯形的高是从上底的任意一点向下底做垂直线段,这个垂直线段就是梯形的高,梯形的上底和下底是平行的,所以从上底可以向下底做无数条垂直线段,因此梯形有无数条高。
【详解】梯形的上底和下底是平行的,两条平行线段之间有无数条垂直线段,梯形也就有无数条高。原题说法正确。
故答案为:√
【点睛】考查梯形特点的相关知识,重点是知道梯形的高有无数条。
19.×
【分析】分析题目,一个平行四边形和一个三角形面积相等,高也相等,则三角形的底是平行四边形底的2倍,据此解答。
【详解】12×2=24(厘米)
三角形的底是24厘米。
故答案为:×
【点睛】掌握面积和高都相等的三角形和平行四边形底之间的关系是解答本题的关键。
20.×
【分析】三角形的面积=底×高÷2,则当两个三角形的底和高相等,它们的面积也相等,但是它们的形状不一定相等,如下图所示,两个三角形底和高都相等,但它们的形状不同。
【详解】根据三角形的面积公式可知,两个三角形的底和高相等,它们的面积相等,但它们的形状不一定相同。原题说法错误。
故答案为:×
【点睛】掌握三角形的特征和面积公式是解题的关键。
21.×
【分析】只有一组对边平行的四边形叫做梯形。平行的两边叫做梯形的底边,较长的一条底边叫下底,较短的一条底边叫上底,另外两边叫腰。夹在两底之间的垂线段是梯形的高,梯形的高与上下底位置相关。
【详解】当梯形的上下底位置一定时,梯形的高与两条侧边变化无关。原题说法错误。
故答案为:×。
【点睛】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。梯形有2条底,有无数条高。
22.13.5 4.5 11.4
【详解】4.5×3=13.5() 3.6×2.5÷2=4.5() (2.4+3.6)×3.8÷2=11.4()
23.4.5m
【分析】平行四边形的高是m,根据等量关系:底×高=平行四边形的面积,列方程解答即可。
【详解】
解:
24.见详解
【分析】三角形的面积=底×高÷2,因为平行线间的距离处处相等,也就是三个三角形的高是相等,画出的锐角三角形、直角三角形和钝角三角形的底相等,那么这三个三角形的面积就相等。
【详解】如图所示:
【点睛】掌握三角形的面积计算公式是解题关键。
25.264厘米
【详解】试题分析:依题意,三个数的末位数字和能被7整除的只有7、14、21等三种.但三个两位的连续偶数相加其和也一定是偶数,故符合题意的只有14.所以三个最小的两位连续偶数它们的末位数字又能被7整除的,便是16、18、20,它们的和即三角形最小周长为16+18+20;这样三个最大的两位连续偶数.它们的末位数字又能被7整除的,便是90、88、86,它们的和即三角形最大周长为90+88+86.
解:依题意,因为三角形三边是三个连续偶数,所以它们的个位数字只能是0,2,4,6,8,并且它们的和也是偶数,
又因为它们的个位数字的和是7的倍数,所以只能是14,
三角形三条边最小应该是:16、18、20,
周长最小为:16+18+20=54(厘米),
三角形三条边最大应该是:86,88,90,
那么周长最长为86+88+90=264(厘米),
答:这个三角形的周长最长应该是264厘米.
点评:此题考查了三角形的特性以及被7整除的数的性质.
26.24007.5元
【分析】先利用梯形的面积公式求出菜地的面积,再乘每平方米收入的钱数,就是总收入,据此解答即可.
【详解】(15+40)×18÷2×48.5,
=55×18÷2×48.5,
=495×48.5,
=24007.5(元),
答:这块菜地一共收入24007.5元钱.
27.4.32
【详解】24×24÷2=288()=0.0288() 0.0288×150=4.32()
答:至少要用4.32布料.
28.160平方厘米
【详解】试题分析:先用“8×5”求出三角形的底的长度,然后根据“三角形的面积=底×高÷2”进行解答即可.
解:8×5=40(厘米),
40×8÷2,
=320÷2,
=160(平方厘米),
答:这个三角形的面积是160平方厘米.
点评:此题考查了三角形的面积公式,利用公式解答即可.
29.6平方厘米;2平方厘米
【详解】试题分析:因为在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,所以两个三角形的面积相等;进而得出甲的面积与三角形DEC的面积相等,即甲的面积是6平方厘米;再根据三角形的面积与底的关系得出BE:ED=18:6=3:1,由此即可求出乙的面积.
解:因为,在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,
所以,三角形ABD与三角形DAC的面积相等,
所以,甲的面积与三角形DEC的面积相等,
甲的面积是6平方厘米,
而,BE:ED=18:6=3:1,
甲的面积:乙的面积=3:1,
乙的面积是:6÷3=2(平方厘米),
答:甲的面积是6平方厘米;乙的面积是2平方厘米.
点评:解答此题的关键是,利用同底等高的性质与三角形的面积与底的关系,得出面积与面积的关系,及边长与面积的关系,从而得出答案.
30.49根
【详解】试题分析:根据堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据进行解答.
解:[4+(7﹣1+4)]×7÷2,
=[4+10]×7÷2,
=14×7÷2,
=49(根).
答:林场一共砍伐了49根树木.
点评:本题主要考查了学生对根数=(上层根数+下层根数)×层数÷2,这一数量关系的掌握情况.
31.264平方米
【分析】梯形的面积=(上底+下底)×高÷2,其中上、下底之和=篱笆总长米数-16,梯形的高就是砖墙长度,据此解答。
【详解】(60-16)×12÷2
=44×6
=264(平方米)
答:这个鸡场的面积大约是264平方米。
【点睛】此题考查了梯形的面积计算,找出梯形的上下底之和以及梯形的高是解题关键。
32.1.1平方米
【详解】试题分析:由题意可知:长方形的面积减去三角形的面积就是剩余的面积,将数据分别代入长方形和三角形的面积公式即可求解.
解:4分米=0.4米,5分米=0.5米,
1.5×0.8﹣0.4×0.5÷2,
=1.2﹣0.1,
=1.1(平方米);
答:剩下的面积是1.1平方米.
点评:此题主要考查长方形和三角形的面积计算方法.
33.125立方米
【详解】试题分析:先根据梯形的面积公式:S=(a+b)h÷2,求出这条水渠的横截面积,再根据V=sh,求出这条水渠挖出土的体积,再除以20,就是平均每天挖土的方数.据此解答.
解:5千米=5000米,
(1.2+0.8)×0.5÷2,
=2×0.5÷2,
=0.5(平方米),
0.5×5000÷20,
=2500÷20,
=125(立方米).
答:平均每天挖土125立方米.
点评:本题的关键是根据V=sh求出这条水渠挖出土的体积,然后再根据除法的意义解答.
34.1215平方米
【详解】试题分析:根据题意,可利用梯形的面积公式确定原来水田的面积,再利用平行四边形的面积公式计算出灌溉水道的面积,最后用原来水田的面积减去灌溉水道占用的面积即可.
解:(60+25)×30×﹣2×30,
=85×30×﹣2×30,
=1275﹣60,
=1215(平方米),
答:水田的面积是1215平方米.
点评:此题主要考查的是梯形的面积公式和平行四边形面积公式的灵活应用.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
