第一单元圆(单元测试)-2024-2025学年六年级数学上册讲练测(北师大版)(含解析)
文档属性
| 名称 | 第一单元圆(单元测试)-2024-2025学年六年级数学上册讲练测(北师大版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 172.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 10:26:21 | ||
图片预览




文档简介
第一单元圆(单元测试)-2024-2025学年六年级数学上册讲练测(北师大版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.( )确定圆的位置。
A.半径 B.直径 C.周长 D.圆心
2.如图,在推导圆面积公式时,通过把圆等分割拼得到一个近似的长方形。这个过程体现的数学思想方法主要是( )思想。
A.抽象 B.集合 C.符号 D.转化
3.一个半圆的半径是3厘米,它的周长是( )厘米。
A.18.84 B.9.42 C.12.42 D.15.42
4.图中阴影部分的面积是空白部分面积的( )
A.一半 B.相等 C.2倍 D.无法比较
5.用46.26米长的水泥墙围一个半圆形游泳池,水的面积是( )平方米。
A.12717 B.254.34 C.127.17 D.25434
6.如图所示,从甲地到乙地有A和B两条路可以走,这两条路的长度相比,( )。
A.A长 B.B 长 C.一样长 D.无法比较
二、填空题
7.把一个周长是6.28分米的圆沿一条直径切成两个半圆,每个半圆的周长是( )分米,面积是( )平方分米。
8.在一块长3m,宽1m的长方形铁板上截下一块最大的半圆形铁板,半圆形周长是( )m,长方形铁板的周长是( )m,面积是( )m 。
9.一个圆环光盘,它的内圆半径是2cm,外圆半径是内圆半径的3倍,这个圆环光盘的面积是( )。
10.算一算,填一填。
钟面 圆形桌面 自行车车轮
半径(r) 80mm 800mm
直径(d) 6.08dm
11.如下图,正方形的周长是20cm,这个圆的周长是( )cm,面积是( )cm2。
12.一个圆环,内圆半径是6厘米,环宽是2厘米,这个圆环的面积是( )平方厘米,这个圆环的外圆周长比内圆周长长( )厘米。
13.圆周率用字母( )表示,保留两位小数取近似值( )。
14.在一个边长8厘米的正方形里,画一个最大的圆,这个圆的直径是( ),半径是( )。
15.下图这个圆的半径是( ),直径是( )。
三、判断题
16.圆的直径扩大到原来的4倍,它的面积扩大到原来的8倍。( )
17.正方形、等腰梯形、三角形和圆都是轴对称图形. ( )
18.在一个正方形里画一个最大的圆,如果这个圆的半径是2厘米,那么这个正方形的边长则是4厘米。( )
19.大小不同的两个圆,其周长与它的直径的商相等。( )
20.圆的周长只与这个圆的直径有关,与圆心的位置无关. ( )
四、计算题
21.直接写出得数。
0.4×0.24= 100×0.039= 0.8×3.14= 2×3.14×3.5=
6.28×0.4= 3.14÷0.1= 31.4÷3.14= 2×3.14×4=
0.7÷0.25= 0.819÷0.9= 0.0942÷0.03= 2×3.14×4.5=
22.计算下面各题,能简算的要简算。
3.14×(24÷6)2 (6.5+12.8)÷2.5÷4 10.8-2.8×0.5-1.33
12.5×(38-30)÷25 5.4×16.7-6.7×5.4 11.05-(6.05-3×1.5)
五、解答题
23.一块圆形花圃,小明绕花圃的外围走一圈,一共走了25.12米。现在花圃的周围铺上2米宽的小路,小路的面积是多少平方米?
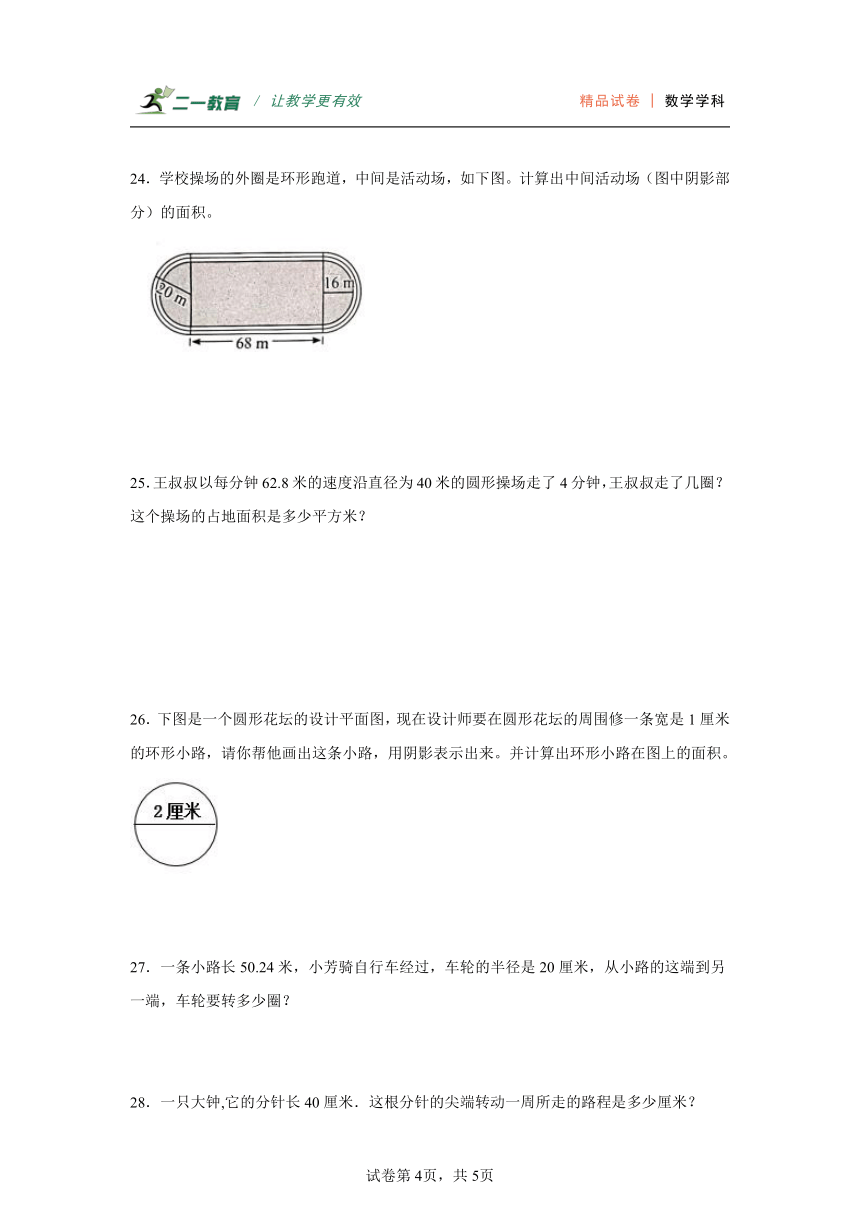
24.学校操场的外圈是环形跑道,中间是活动场,如下图。计算出中间活动场(图中阴影部分)的面积。
25.王叔叔以每分钟62.8米的速度沿直径为40米的圆形操场走了4分钟,王叔叔走了几圈?这个操场的占地面积是多少平方米?
26.下图是一个圆形花坛的设计平面图,现在设计师要在圆形花坛的周围修一条宽是1厘米的环形小路,请你帮他画出这条小路,用阴影表示出来。并计算出环形小路在图上的面积。
27.一条小路长50.24米,小芳骑自行车经过,车轮的半径是20厘米,从小路的这端到另一端,车轮要转多少圈?
28.一只大钟,它的分针长40厘米.这根分针的尖端转动一周所走的路程是多少厘米?
29.画两条互相垂直的直线,标出交点O.以O点为圆心画一个直径是3厘米的圆.
30.一只羊栓在一个木桩上,绳子从木桩到羊颈部长5米,这只羊最多能吃到青草的面积是多少平方米?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】在画圆的的时候,圆规的针尖在哪里,圆心就在哪里。针尖移动位置,圆心的位置也变,圆的位置也跟着改变。由此即可知道圆心决定圆的位置。
故答案为:D。
2.D
【分析】在推导圆面积公式时,通过把圆等分割拼得到一个近似的长方形,长方形的长是圆周长的一半,长方形的宽是圆的半径,这里用到了转化和近似的思想。
【详解】通过把圆等分割拼得到一个近似的长方形,推导圆面积公式这个过程体现的数学思想方法主要是转化思想。
故答案选:D。
【点睛】随后学习圆柱的体积是,也会用到转化的思想,将圆柱剪拼成近似的长方体。
3.D
【分析】
半圆的周长=圆周长的一半+直径=πr+2r,据此代入数据计算即可解答。
【详解】3.14×3+2×3
=9.42+6
=15.42(厘米)
则它的周长是15.42厘米。
故答案为:D
4.A
【分析】观察图形可知,正方形与三角形等底等高,根据正方形的面积与三角形的面积公式可知,三角形的面积是与它等底等高的正方形的面积的一半,由此即可解答.
【详解】因为三角形的面积是与它等底等高的正方形的面积的一半,所以图中三角形的面积是正方形面积的一半.
故选A.
5.C
【分析】根据半圆周长的意义,半圆周长等于这个圆的周长一半加上一条直径的长,设这个圆的半径为x米,列方程:2x+3.14x=46.26,解方程,求出半圆的半径,求水的面积,就是求这个圆的面积的一半,根据圆的面积公式:面积=π×半径2;代入数据,求出圆的面积,再除以2,即可解答。
【详解】解:设圆的半径为x米。
2x+3.14x=46.26
5.14x=46.26
x=46.26÷5.14
x=9
3.14×92÷2
=3.14×81÷2
=254.34÷2
=127.17(平方米)
用46.26米长的水泥墙围一个半圆形游泳池,水的面积是127.17平方米。
故答案为:C
【点睛】本题考查半圆的周长和圆的面积公式的应用,关键明确半圆周长是该圆的周长一半加上一条直径的长度。
6.C
【分析】观察图形A路线是一个大的半圆,B路线是两个小半圆与一个中半圆,其中两个小半圆相等,小半圆的直径等于中半圆的半径,大半圆的半径等于中半圆的直径,设小半圆的直径是1,则中半圆的直径为1×2=2,大半圆的直径为2×2,根据圆的周长公式:周长=π×直径,代入数据,求出A路线和B路线的长,再进行比较,即可解答。
【详解】设小半圆的直径为1,则中半圆的直径为1×2=2;大半圆的直径为2×2=4。
A路线:π×4÷2
=2π
B路线:π×1÷2×2+π×2÷2
=0.5×2π+π
=π+π
=2π
2π=2π
A路线=B路线
如图所示,从甲地到乙地有A和B两条路可以走,这两条路的长度相比,一样长。
故答案为:C
【点睛】本题关键在于圆或半圆的周长的计算方法,半圆的周长是整圆的一半。
7. 5.14 1.57
【分析】已知圆的周长C=πd,则d=C÷π,据此求出圆的直径,半圆的周长=圆的周长÷2+直径,半圆的面积=圆的面积÷2,据此解答。
【详解】6.28÷3.14=2(分米)
6.28÷2+2
=3.14+2
=5.14(分米)
半圆的周长是5.14分米;
3.14×(2÷2)2÷2
=3.14÷2
=1.57(平方分米)
半圆的面积是1.57平方分米。
【点睛】此题考查半圆的周长和面积的计算,注意半圆的周长需要加一条直径的长度。
8. 5.14 8 3
【分析】根据题意可知:在这个长方形铁板上截下一块最大的半圆形铁板,半圆形铁板的半径等于长方形的宽,根据半圆的周长=圆周率×直径÷2+直径,计算半圆形周长,根据长方形周长公式和面积公式分别计算长方形铁板的周长和面积。
【详解】半圆形周长:
3.14×(2×1)÷2+(2×1)
=3.14×2÷2+2
=5.14(米)
长方形铁板的周长:
(3+1)×2
=4×2
=8(米)
长方形铁板的面积:3×1=3(平方米)
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
9.100.48
【分析】,R表示外圆的半径,r表示内圆的半径,先求出外圆的半径,再据此公式可求出圆环光盘的面积。
【详解】由分析可知:
R:2×3=6(cm)
所以这个圆环光盘的面积是100.48。
【点睛】本题考查圆环面积的应用,学生需熟练掌握圆环的面积公式。
10.见详解
【分析】根据圆的直径是半径的2倍,已知半径可用半径乘2求直径,已知直径可用直径除以2求半径。据此解答。
【详解】(dm)
(mm)
(mm)
钟面 圆形桌面 自行车车轮
半径(r) 80mm 800mm 3.04dm
直径(d) 160mm 1600mm 6.08dm
11. 31.4 78.5
【分析】已知正方形的周长是20cm,根据正方形的周长=边长×4,代入数据求出正方形的边长,即圆的半径;再利用圆的周长公式:C=,圆的面积公式:S=,代入数据即可求出圆的周长和圆的面积。
【详解】20÷4=5(cm)
2×3.14×5=31.4(cm)
3.14×52
=3.14×25
=78.5(cm2)
即这个圆的周长是31.4cm,面积是78.5cm2。
【点睛】此题的解题关键是先求出圆的半径,利用正方形的周长公式、圆的周长公式以及圆的面积公式解决问题。
12. 87.92 12.56
【分析】内圆半径是6厘米,环宽是2厘米,则外圆半径是6+2=8厘米,带入圆环的面积公式即可求出圆环的面积;将数据代入圆的周长公式分别求出内、外圆的周长,再求差即可。
【详解】6+2=8(厘米)
3.14×(82-62)
=3.14×28
=87.92(平方厘米)
3.14×8×2-3.14×6×2
=3.14×(16-12)
=3.14×4
=12.56(厘米)
【点睛】本题主要考查圆环的面积公式及圆的周长公式的灵活运用。
13. π 3.14
【分析】根据教材中关于圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,保留两位小数后的近似值是3.14,解答即可。
【详解】圆周率用字母π表示,保留两位小数取近似值3.14。
【点睛】此题考查的是圆周率的知识,应多注意基础知识的理解和掌握。
14. 8厘米 4厘米
【分析】在正方形里画一个最大的圆,则圆的直径就是正方形的边长,已知正方形边长为8厘米,所以圆的半径可求。
【详解】如图:
这个圆的直径是8厘米,半径是:8÷2=4(厘米)
【点睛】此题主要考查的是:在一个正方形内画一个最大的圆,正方形的边长即是这个圆的直径。
15. 1.8cm 3.6cm
【分析】观察图形可知,圆的半径是1.8cm,再根据在同一个圆里,圆的直径是半径的2倍,用1.8×2,求出直径。
【详解】半径是:1.8cm
直径是:1.8×2=3.6(cm)
这个圆的半径是1.8cm,直径是3.6cm。
【点睛】本题考查圆的特征,以及圆的半径与直径的关系。
16.×
【分析】根据圆的面积公式:S=πr2,同时直径=半径×2,可以假设原来的圆的半径为1,将数据代入公式求出扩大后面积的值,进行判断即可。
【详解】由分析可得:
假设圆的半径为1,该圆的直径为l×2=2,
直径扩大到原来的4倍,即扩大后圆的直径为:2×4=8,
扩大后圆的半径为:8÷2=4,
原来圆的面积:3.14×12=3.14
扩大后圆的面积:3.14×42=50.24
面积扩大的倍数为:50.24÷3.14=16
综上所述:一个圆的直径扩大到原来的4倍,那么它的面积扩大到原来的16倍,原题说法错误。
故答案为:×
17.×
【详解】略
18.√
【分析】在一个正方形里画一个最大的圆,这个正方形的边长等于圆的直径,据此解答。
【详解】这个圆的半径是2厘米,这个正方形的边长则等于圆的直径,2×2=4厘米。
故答案为:√
【点睛】本题主要考查正方形和正方形内的圆的关系。
19.√
【分析】根据圆周率的意义,任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,一般用“π”表示。由此判断。
【详解】根据圆周率的意义可知,每个圆的圆周率都是π,所以每个圆的圆周率都相等。
周长÷直径=π(一定)
所以,大小不同的两个圆,其周长与它的直径的商相等。
原题说法正确。
故答案为:√
【点睛】本题考查圆周率的认识,明确圆周率是一个固定的数,不随圆的大小而变化。
20.√
【详解】略
21.0.096;3.9;2.512;21.98;
2.512;31.4;10;25.12;
2.8;0.91;3.14;28.26
【详解】略
22.50.24;1.93;8.07;
4;54;9.5
【分析】先算小括号里面的除法,再算乘方,最后算乘法;
先算小括号里面的加法,再根据除法的性质进行简算;
先算乘法,再从左到右依次计算;
先算小括号里面的减法,再算乘法最后算除法;
根据乘法分配律进行简算;
先算小括号里面的乘法,再根据减法的性质进行简算。
【详解】3.14×(24÷6)2
=3.14×16
=50.24
(6.5+12.8)÷2.5÷4
=19.3÷(2.5×4)
=19.3÷10
=1.93
10.8-2.8×0.5-1.33
=10.8-1.4-1.33
=9.4-1.33
=8.07
12.5×(38-30)÷25
=12.5×8÷25
=100÷25
=4
5.4×16.7-6.7×5.4
=5.4×(16.7-6.7)
=5.4×10
=54
11.05-(6.05-3×1.5)
=11.05-6.05+4.5
=5+4.5
=9.5
23.62.8平方米
【分析】求小路的面积就是求圆环的面积。根据题意,花圃的周长是25.12米,而圆的周长=2πr,据此用25.12除以2π即可求出圆的半径,即内圆的半径。内圆的半径加上小路的宽即是外圆的半径。圆环的面积=π(R2-r2),据此求出小路的面积。
【详解】25.12÷3.14÷2=4(米)
4+2=6(米)
3.14×(62-42)
=3.14×20
=62.8(平方米)
答:小路的面积是62.8平方米。
【点睛】本题考查了圆的周长和圆环的面积的应用。掌握并熟练运用圆的周长和圆环的面积公式是解题的关键。
24.2979.84平方米
【分析】看图,活动场的面积=中间长方形的面积+半径为16米的圆的面积。长方形面积=长×宽,圆的面积=πr2,据此列式解题即可。
【详解】16×2=32(米)
68×32+3.14×162
=2176+803.84
=2979.84(平方米)
答:中间活动场的面积是2979.84平方米。
【点睛】本题考查了阴影部分的面积,熟练运用割补法,掌握长方形和圆的面积公式是解题的关键。
25.2圈;1256平方米
【分析】利用速度×时间=路程,代入数据求出王叔叔所走的路程,再根据圆的周长公式:C=,求出这个圆形操场一圈的长度,再用王叔叔所走的路程除以圆形操场一圈的长度,即可求出王叔叔走了几圈;最后根据圆的面积公式:S=,代入数据即可求出这个操场的占地面积是多少平方米。
【详解】3.14×40=125.6(米)
62.8×4=251.2(米)
251.2÷125.6=2(圈)
3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:王叔叔走了2圈,这个操场的占地面积是1256平方米。
【点睛】此题主要考查圆的周长、圆的面积的计算方法,熟记公式是解题关键。
26.;9.42平方厘米
【分析】花坛是内圆,花坛的直径是2厘米,半径是2÷2=1厘米,用1厘米+1厘米=2厘米,画出半径是2厘米的外圆,修的这条环形小路就是一个圆环,利用圆环的面积公式即可解答。
【详解】根据题意,画图如下:
内圆面积:
3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
外圆面积:
3.14×(1+1)2
=3.14×4
=12.56(平方厘米)
环形小路面积:
12.56-3.14=9.42(平方厘米)
答:环形小路在图上的面积是9.42平方厘米。
【点睛】此题考查了圆环的面积公式的灵活应用。
27.40圈
【详解】20厘米=0.2米
50.24÷(3.14×2×0.2)=40(圈)
28.251.2厘米
【详解】3.14×40×2=251.2(厘米)
29.如图
【详解】试题分析:先任意画一条直线,再过直线上任意一点作这条直线的垂线;然后可以画出直径是3厘米的圆.
解:如图所示:
先任意画一条直线,再过直线上任意一点作这条直线的垂线,垂足为O;然后以O为圆心,以厘米为半径即可画圆.
点评:此题主要考查过直线上一点作直线的垂线的作法及圆的画法.
30.78.5平方米
【分析】观察题意可知,羊能吃到青草的面积相当于一个半径为5米的圆面积,根据圆面积公式:S=πr2,用3.14×52即可求出羊能吃到青草的面积。
【详解】3.14×52
=3.14×25
=78.5(平方米)
答:这只羊最多能吃到青草的面积是78.5平方米。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.( )确定圆的位置。
A.半径 B.直径 C.周长 D.圆心
2.如图,在推导圆面积公式时,通过把圆等分割拼得到一个近似的长方形。这个过程体现的数学思想方法主要是( )思想。
A.抽象 B.集合 C.符号 D.转化
3.一个半圆的半径是3厘米,它的周长是( )厘米。
A.18.84 B.9.42 C.12.42 D.15.42
4.图中阴影部分的面积是空白部分面积的( )
A.一半 B.相等 C.2倍 D.无法比较
5.用46.26米长的水泥墙围一个半圆形游泳池,水的面积是( )平方米。
A.12717 B.254.34 C.127.17 D.25434
6.如图所示,从甲地到乙地有A和B两条路可以走,这两条路的长度相比,( )。
A.A长 B.B 长 C.一样长 D.无法比较
二、填空题
7.把一个周长是6.28分米的圆沿一条直径切成两个半圆,每个半圆的周长是( )分米,面积是( )平方分米。
8.在一块长3m,宽1m的长方形铁板上截下一块最大的半圆形铁板,半圆形周长是( )m,长方形铁板的周长是( )m,面积是( )m 。
9.一个圆环光盘,它的内圆半径是2cm,外圆半径是内圆半径的3倍,这个圆环光盘的面积是( )。
10.算一算,填一填。
钟面 圆形桌面 自行车车轮
半径(r) 80mm 800mm
直径(d) 6.08dm
11.如下图,正方形的周长是20cm,这个圆的周长是( )cm,面积是( )cm2。
12.一个圆环,内圆半径是6厘米,环宽是2厘米,这个圆环的面积是( )平方厘米,这个圆环的外圆周长比内圆周长长( )厘米。
13.圆周率用字母( )表示,保留两位小数取近似值( )。
14.在一个边长8厘米的正方形里,画一个最大的圆,这个圆的直径是( ),半径是( )。
15.下图这个圆的半径是( ),直径是( )。
三、判断题
16.圆的直径扩大到原来的4倍,它的面积扩大到原来的8倍。( )
17.正方形、等腰梯形、三角形和圆都是轴对称图形. ( )
18.在一个正方形里画一个最大的圆,如果这个圆的半径是2厘米,那么这个正方形的边长则是4厘米。( )
19.大小不同的两个圆,其周长与它的直径的商相等。( )
20.圆的周长只与这个圆的直径有关,与圆心的位置无关. ( )
四、计算题
21.直接写出得数。
0.4×0.24= 100×0.039= 0.8×3.14= 2×3.14×3.5=
6.28×0.4= 3.14÷0.1= 31.4÷3.14= 2×3.14×4=
0.7÷0.25= 0.819÷0.9= 0.0942÷0.03= 2×3.14×4.5=
22.计算下面各题,能简算的要简算。
3.14×(24÷6)2 (6.5+12.8)÷2.5÷4 10.8-2.8×0.5-1.33
12.5×(38-30)÷25 5.4×16.7-6.7×5.4 11.05-(6.05-3×1.5)
五、解答题
23.一块圆形花圃,小明绕花圃的外围走一圈,一共走了25.12米。现在花圃的周围铺上2米宽的小路,小路的面积是多少平方米?
24.学校操场的外圈是环形跑道,中间是活动场,如下图。计算出中间活动场(图中阴影部分)的面积。
25.王叔叔以每分钟62.8米的速度沿直径为40米的圆形操场走了4分钟,王叔叔走了几圈?这个操场的占地面积是多少平方米?
26.下图是一个圆形花坛的设计平面图,现在设计师要在圆形花坛的周围修一条宽是1厘米的环形小路,请你帮他画出这条小路,用阴影表示出来。并计算出环形小路在图上的面积。
27.一条小路长50.24米,小芳骑自行车经过,车轮的半径是20厘米,从小路的这端到另一端,车轮要转多少圈?
28.一只大钟,它的分针长40厘米.这根分针的尖端转动一周所走的路程是多少厘米?
29.画两条互相垂直的直线,标出交点O.以O点为圆心画一个直径是3厘米的圆.
30.一只羊栓在一个木桩上,绳子从木桩到羊颈部长5米,这只羊最多能吃到青草的面积是多少平方米?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】在画圆的的时候,圆规的针尖在哪里,圆心就在哪里。针尖移动位置,圆心的位置也变,圆的位置也跟着改变。由此即可知道圆心决定圆的位置。
故答案为:D。
2.D
【分析】在推导圆面积公式时,通过把圆等分割拼得到一个近似的长方形,长方形的长是圆周长的一半,长方形的宽是圆的半径,这里用到了转化和近似的思想。
【详解】通过把圆等分割拼得到一个近似的长方形,推导圆面积公式这个过程体现的数学思想方法主要是转化思想。
故答案选:D。
【点睛】随后学习圆柱的体积是,也会用到转化的思想,将圆柱剪拼成近似的长方体。
3.D
【分析】
半圆的周长=圆周长的一半+直径=πr+2r,据此代入数据计算即可解答。
【详解】3.14×3+2×3
=9.42+6
=15.42(厘米)
则它的周长是15.42厘米。
故答案为:D
4.A
【分析】观察图形可知,正方形与三角形等底等高,根据正方形的面积与三角形的面积公式可知,三角形的面积是与它等底等高的正方形的面积的一半,由此即可解答.
【详解】因为三角形的面积是与它等底等高的正方形的面积的一半,所以图中三角形的面积是正方形面积的一半.
故选A.
5.C
【分析】根据半圆周长的意义,半圆周长等于这个圆的周长一半加上一条直径的长,设这个圆的半径为x米,列方程:2x+3.14x=46.26,解方程,求出半圆的半径,求水的面积,就是求这个圆的面积的一半,根据圆的面积公式:面积=π×半径2;代入数据,求出圆的面积,再除以2,即可解答。
【详解】解:设圆的半径为x米。
2x+3.14x=46.26
5.14x=46.26
x=46.26÷5.14
x=9
3.14×92÷2
=3.14×81÷2
=254.34÷2
=127.17(平方米)
用46.26米长的水泥墙围一个半圆形游泳池,水的面积是127.17平方米。
故答案为:C
【点睛】本题考查半圆的周长和圆的面积公式的应用,关键明确半圆周长是该圆的周长一半加上一条直径的长度。
6.C
【分析】观察图形A路线是一个大的半圆,B路线是两个小半圆与一个中半圆,其中两个小半圆相等,小半圆的直径等于中半圆的半径,大半圆的半径等于中半圆的直径,设小半圆的直径是1,则中半圆的直径为1×2=2,大半圆的直径为2×2,根据圆的周长公式:周长=π×直径,代入数据,求出A路线和B路线的长,再进行比较,即可解答。
【详解】设小半圆的直径为1,则中半圆的直径为1×2=2;大半圆的直径为2×2=4。
A路线:π×4÷2
=2π
B路线:π×1÷2×2+π×2÷2
=0.5×2π+π
=π+π
=2π
2π=2π
A路线=B路线
如图所示,从甲地到乙地有A和B两条路可以走,这两条路的长度相比,一样长。
故答案为:C
【点睛】本题关键在于圆或半圆的周长的计算方法,半圆的周长是整圆的一半。
7. 5.14 1.57
【分析】已知圆的周长C=πd,则d=C÷π,据此求出圆的直径,半圆的周长=圆的周长÷2+直径,半圆的面积=圆的面积÷2,据此解答。
【详解】6.28÷3.14=2(分米)
6.28÷2+2
=3.14+2
=5.14(分米)
半圆的周长是5.14分米;
3.14×(2÷2)2÷2
=3.14÷2
=1.57(平方分米)
半圆的面积是1.57平方分米。
【点睛】此题考查半圆的周长和面积的计算,注意半圆的周长需要加一条直径的长度。
8. 5.14 8 3
【分析】根据题意可知:在这个长方形铁板上截下一块最大的半圆形铁板,半圆形铁板的半径等于长方形的宽,根据半圆的周长=圆周率×直径÷2+直径,计算半圆形周长,根据长方形周长公式和面积公式分别计算长方形铁板的周长和面积。
【详解】半圆形周长:
3.14×(2×1)÷2+(2×1)
=3.14×2÷2+2
=5.14(米)
长方形铁板的周长:
(3+1)×2
=4×2
=8(米)
长方形铁板的面积:3×1=3(平方米)
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
9.100.48
【分析】,R表示外圆的半径,r表示内圆的半径,先求出外圆的半径,再据此公式可求出圆环光盘的面积。
【详解】由分析可知:
R:2×3=6(cm)
所以这个圆环光盘的面积是100.48。
【点睛】本题考查圆环面积的应用,学生需熟练掌握圆环的面积公式。
10.见详解
【分析】根据圆的直径是半径的2倍,已知半径可用半径乘2求直径,已知直径可用直径除以2求半径。据此解答。
【详解】(dm)
(mm)
(mm)
钟面 圆形桌面 自行车车轮
半径(r) 80mm 800mm 3.04dm
直径(d) 160mm 1600mm 6.08dm
11. 31.4 78.5
【分析】已知正方形的周长是20cm,根据正方形的周长=边长×4,代入数据求出正方形的边长,即圆的半径;再利用圆的周长公式:C=,圆的面积公式:S=,代入数据即可求出圆的周长和圆的面积。
【详解】20÷4=5(cm)
2×3.14×5=31.4(cm)
3.14×52
=3.14×25
=78.5(cm2)
即这个圆的周长是31.4cm,面积是78.5cm2。
【点睛】此题的解题关键是先求出圆的半径,利用正方形的周长公式、圆的周长公式以及圆的面积公式解决问题。
12. 87.92 12.56
【分析】内圆半径是6厘米,环宽是2厘米,则外圆半径是6+2=8厘米,带入圆环的面积公式即可求出圆环的面积;将数据代入圆的周长公式分别求出内、外圆的周长,再求差即可。
【详解】6+2=8(厘米)
3.14×(82-62)
=3.14×28
=87.92(平方厘米)
3.14×8×2-3.14×6×2
=3.14×(16-12)
=3.14×4
=12.56(厘米)
【点睛】本题主要考查圆环的面积公式及圆的周长公式的灵活运用。
13. π 3.14
【分析】根据教材中关于圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,保留两位小数后的近似值是3.14,解答即可。
【详解】圆周率用字母π表示,保留两位小数取近似值3.14。
【点睛】此题考查的是圆周率的知识,应多注意基础知识的理解和掌握。
14. 8厘米 4厘米
【分析】在正方形里画一个最大的圆,则圆的直径就是正方形的边长,已知正方形边长为8厘米,所以圆的半径可求。
【详解】如图:
这个圆的直径是8厘米,半径是:8÷2=4(厘米)
【点睛】此题主要考查的是:在一个正方形内画一个最大的圆,正方形的边长即是这个圆的直径。
15. 1.8cm 3.6cm
【分析】观察图形可知,圆的半径是1.8cm,再根据在同一个圆里,圆的直径是半径的2倍,用1.8×2,求出直径。
【详解】半径是:1.8cm
直径是:1.8×2=3.6(cm)
这个圆的半径是1.8cm,直径是3.6cm。
【点睛】本题考查圆的特征,以及圆的半径与直径的关系。
16.×
【分析】根据圆的面积公式:S=πr2,同时直径=半径×2,可以假设原来的圆的半径为1,将数据代入公式求出扩大后面积的值,进行判断即可。
【详解】由分析可得:
假设圆的半径为1,该圆的直径为l×2=2,
直径扩大到原来的4倍,即扩大后圆的直径为:2×4=8,
扩大后圆的半径为:8÷2=4,
原来圆的面积:3.14×12=3.14
扩大后圆的面积:3.14×42=50.24
面积扩大的倍数为:50.24÷3.14=16
综上所述:一个圆的直径扩大到原来的4倍,那么它的面积扩大到原来的16倍,原题说法错误。
故答案为:×
17.×
【详解】略
18.√
【分析】在一个正方形里画一个最大的圆,这个正方形的边长等于圆的直径,据此解答。
【详解】这个圆的半径是2厘米,这个正方形的边长则等于圆的直径,2×2=4厘米。
故答案为:√
【点睛】本题主要考查正方形和正方形内的圆的关系。
19.√
【分析】根据圆周率的意义,任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,一般用“π”表示。由此判断。
【详解】根据圆周率的意义可知,每个圆的圆周率都是π,所以每个圆的圆周率都相等。
周长÷直径=π(一定)
所以,大小不同的两个圆,其周长与它的直径的商相等。
原题说法正确。
故答案为:√
【点睛】本题考查圆周率的认识,明确圆周率是一个固定的数,不随圆的大小而变化。
20.√
【详解】略
21.0.096;3.9;2.512;21.98;
2.512;31.4;10;25.12;
2.8;0.91;3.14;28.26
【详解】略
22.50.24;1.93;8.07;
4;54;9.5
【分析】先算小括号里面的除法,再算乘方,最后算乘法;
先算小括号里面的加法,再根据除法的性质进行简算;
先算乘法,再从左到右依次计算;
先算小括号里面的减法,再算乘法最后算除法;
根据乘法分配律进行简算;
先算小括号里面的乘法,再根据减法的性质进行简算。
【详解】3.14×(24÷6)2
=3.14×16
=50.24
(6.5+12.8)÷2.5÷4
=19.3÷(2.5×4)
=19.3÷10
=1.93
10.8-2.8×0.5-1.33
=10.8-1.4-1.33
=9.4-1.33
=8.07
12.5×(38-30)÷25
=12.5×8÷25
=100÷25
=4
5.4×16.7-6.7×5.4
=5.4×(16.7-6.7)
=5.4×10
=54
11.05-(6.05-3×1.5)
=11.05-6.05+4.5
=5+4.5
=9.5
23.62.8平方米
【分析】求小路的面积就是求圆环的面积。根据题意,花圃的周长是25.12米,而圆的周长=2πr,据此用25.12除以2π即可求出圆的半径,即内圆的半径。内圆的半径加上小路的宽即是外圆的半径。圆环的面积=π(R2-r2),据此求出小路的面积。
【详解】25.12÷3.14÷2=4(米)
4+2=6(米)
3.14×(62-42)
=3.14×20
=62.8(平方米)
答:小路的面积是62.8平方米。
【点睛】本题考查了圆的周长和圆环的面积的应用。掌握并熟练运用圆的周长和圆环的面积公式是解题的关键。
24.2979.84平方米
【分析】看图,活动场的面积=中间长方形的面积+半径为16米的圆的面积。长方形面积=长×宽,圆的面积=πr2,据此列式解题即可。
【详解】16×2=32(米)
68×32+3.14×162
=2176+803.84
=2979.84(平方米)
答:中间活动场的面积是2979.84平方米。
【点睛】本题考查了阴影部分的面积,熟练运用割补法,掌握长方形和圆的面积公式是解题的关键。
25.2圈;1256平方米
【分析】利用速度×时间=路程,代入数据求出王叔叔所走的路程,再根据圆的周长公式:C=,求出这个圆形操场一圈的长度,再用王叔叔所走的路程除以圆形操场一圈的长度,即可求出王叔叔走了几圈;最后根据圆的面积公式:S=,代入数据即可求出这个操场的占地面积是多少平方米。
【详解】3.14×40=125.6(米)
62.8×4=251.2(米)
251.2÷125.6=2(圈)
3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:王叔叔走了2圈,这个操场的占地面积是1256平方米。
【点睛】此题主要考查圆的周长、圆的面积的计算方法,熟记公式是解题关键。
26.;9.42平方厘米
【分析】花坛是内圆,花坛的直径是2厘米,半径是2÷2=1厘米,用1厘米+1厘米=2厘米,画出半径是2厘米的外圆,修的这条环形小路就是一个圆环,利用圆环的面积公式即可解答。
【详解】根据题意,画图如下:
内圆面积:
3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
外圆面积:
3.14×(1+1)2
=3.14×4
=12.56(平方厘米)
环形小路面积:
12.56-3.14=9.42(平方厘米)
答:环形小路在图上的面积是9.42平方厘米。
【点睛】此题考查了圆环的面积公式的灵活应用。
27.40圈
【详解】20厘米=0.2米
50.24÷(3.14×2×0.2)=40(圈)
28.251.2厘米
【详解】3.14×40×2=251.2(厘米)
29.如图
【详解】试题分析:先任意画一条直线,再过直线上任意一点作这条直线的垂线;然后可以画出直径是3厘米的圆.
解:如图所示:
先任意画一条直线,再过直线上任意一点作这条直线的垂线,垂足为O;然后以O为圆心,以厘米为半径即可画圆.
点评:此题主要考查过直线上一点作直线的垂线的作法及圆的画法.
30.78.5平方米
【分析】观察题意可知,羊能吃到青草的面积相当于一个半径为5米的圆面积,根据圆面积公式:S=πr2,用3.14×52即可求出羊能吃到青草的面积。
【详解】3.14×52
=3.14×25
=78.5(平方米)
答:这只羊最多能吃到青草的面积是78.5平方米。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
