4.3解直角三角形 课件(共13张PPT)
文档属性
| 名称 | 4.3解直角三角形 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
4.3 解直角三角形
1、体会锐角三角函数在解决问题中的作用;
2、能够把实际问题转化为数学问题,发展数学应用意识和解决问题的能力.
A
C
B
c
b
a
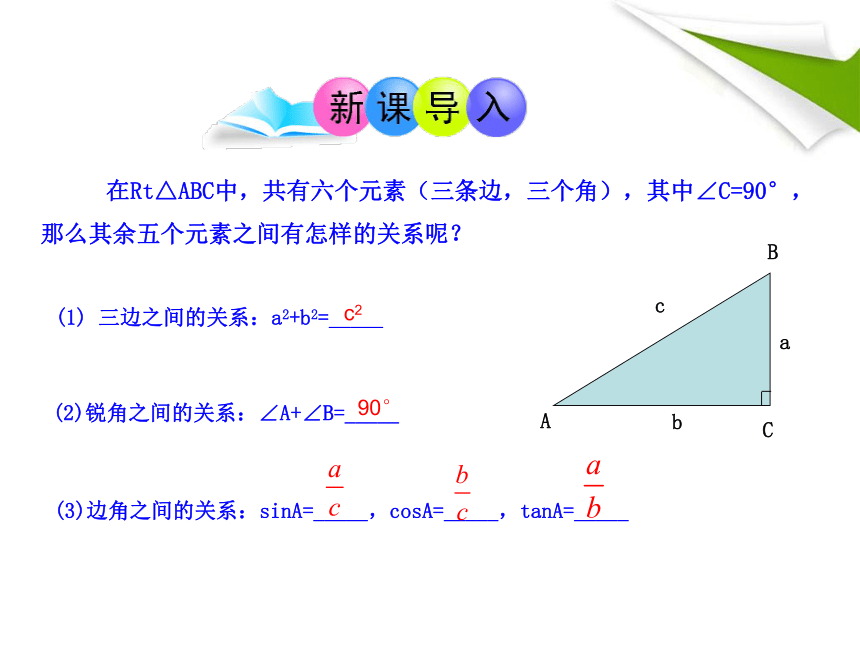
(1) 三边之间的关系:a2+b2=_____
(2)锐角之间的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
我们把在直角三角形中利用已知元素求其余未知元素的过程叫作解直角三角形.
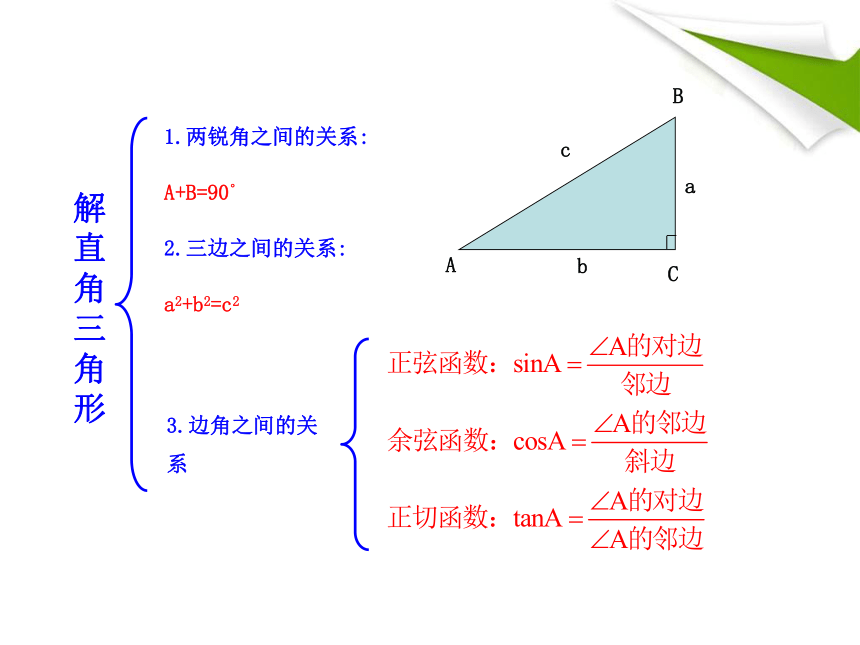
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=90°
a2+b2=c2
A
C
B
c
b
a
如图,在Rt△ABC中,∠C=90°,∠A=42°6′,c=30.解这个直角三角形.
解:∠B=90°-42°6′=47°54′,
b=c·cosA=30×0.7420=22.26.
A
C
b
a
B
c
a=c·sinA=30×0.6704=20.112.
例 题
动脑筋
1.如图,从点C测得树的顶角为33 ,BC=20米,则树高AB=___ 米.(用计算器计算,结果精确到0.1米)
AB=BC·tanC=20×tan33°=13.0.
【解析】
【答案】13.0.
规律方法:在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
想一想
如图,△ABC中,∠C=90°,AB=8,
cosA= ,则AC的长是_______.
A
C
B
6
2.在Rt△ABC中,若AC=2BC,则sinA的值是( )
C
4.如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB= ,则AC=____.
3.在△ABC中,∠C=90°,sinA= ,
则tanB为( )
B
A
B
C
D
5
5.已知:如图,在Rt△ABC中,∠C=90°,AC= .点D为BC边上一点,且BD=2AD,∠ADC=60°.求△ABC的周长(结果保留根号).
解析:要求△ABC的周长,只要求得BC及AB的长度即可.根据Rt△ADC中∠ADC的正弦值,可以求得AD的长度,也可求得CD的长度;再根据已知条件求得BD的长度,继而求得BC的长度;运用勾股定理可以求得AB的长度,求得△ABC的周长.
通过这节课,我们应当掌握:
1、掌握直角三角形的五个元素,已知两个元素(至少有个是边),能求出其余三个元素;
2、能把数学问题转化成解直角三角形问题.
4.3 解直角三角形
1、体会锐角三角函数在解决问题中的作用;
2、能够把实际问题转化为数学问题,发展数学应用意识和解决问题的能力.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____
(2)锐角之间的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
我们把在直角三角形中利用已知元素求其余未知元素的过程叫作解直角三角形.
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=90°
a2+b2=c2
A
C
B
c
b
a
如图,在Rt△ABC中,∠C=90°,∠A=42°6′,c=30.解这个直角三角形.
解:∠B=90°-42°6′=47°54′,
b=c·cosA=30×0.7420=22.26.
A
C
b
a
B
c
a=c·sinA=30×0.6704=20.112.
例 题
动脑筋
1.如图,从点C测得树的顶角为33 ,BC=20米,则树高AB=___ 米.(用计算器计算,结果精确到0.1米)
AB=BC·tanC=20×tan33°=13.0.
【解析】
【答案】13.0.
规律方法:在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
想一想
如图,△ABC中,∠C=90°,AB=8,
cosA= ,则AC的长是_______.
A
C
B
6
2.在Rt△ABC中,若AC=2BC,则sinA的值是( )
C
4.如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB= ,则AC=____.
3.在△ABC中,∠C=90°,sinA= ,
则tanB为( )
B
A
B
C
D
5
5.已知:如图,在Rt△ABC中,∠C=90°,AC= .点D为BC边上一点,且BD=2AD,∠ADC=60°.求△ABC的周长(结果保留根号).
解析:要求△ABC的周长,只要求得BC及AB的长度即可.根据Rt△ADC中∠ADC的正弦值,可以求得AD的长度,也可求得CD的长度;再根据已知条件求得BD的长度,继而求得BC的长度;运用勾股定理可以求得AB的长度,求得△ABC的周长.
通过这节课,我们应当掌握:
1、掌握直角三角形的五个元素,已知两个元素(至少有个是边),能求出其余三个元素;
2、能把数学问题转化成解直角三角形问题.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
