湖南省衡阳县2015-2016学年高中物理上学期期末复习十 滑块-木板模型问题学案
文档属性
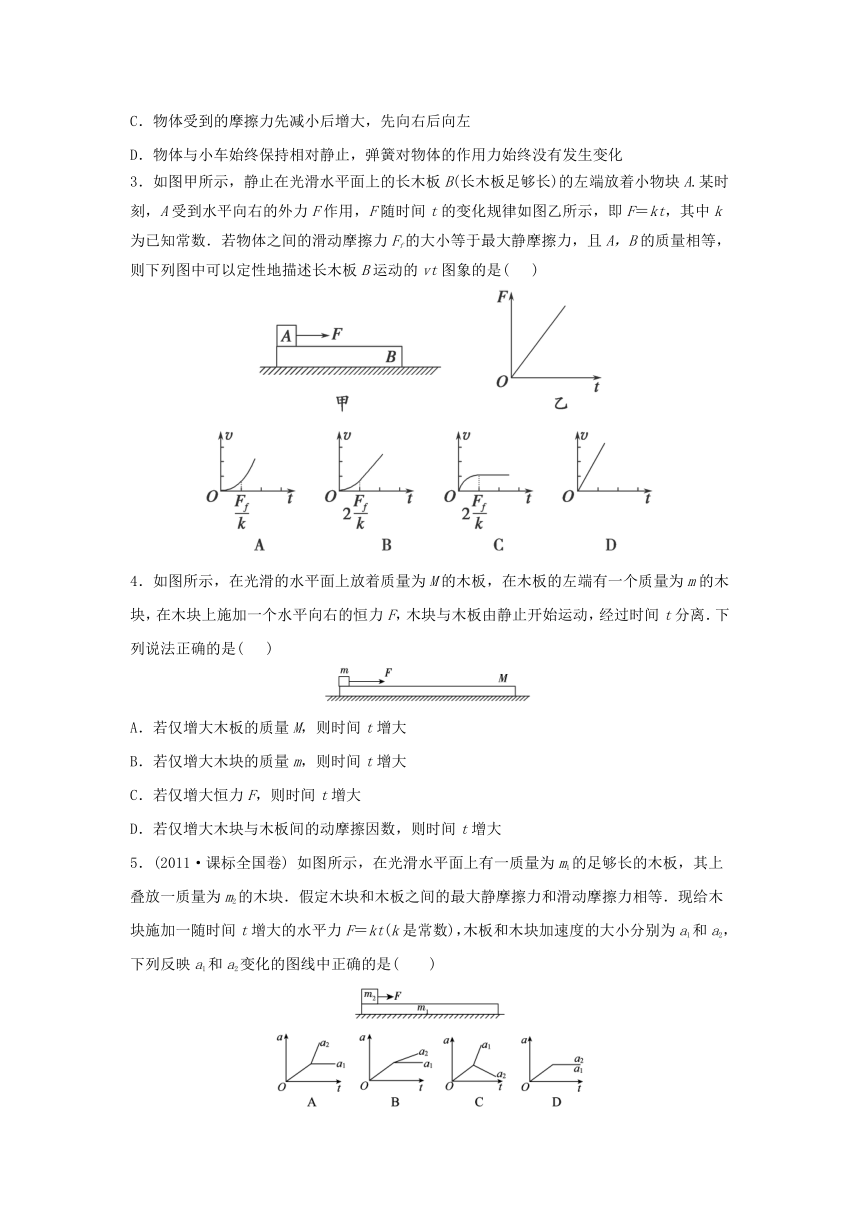
| 名称 | 湖南省衡阳县2015-2016学年高中物理上学期期末复习十 滑块-木板模型问题学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-02-14 19:49:06 | ||
图片预览



文档简介
期末复习学案十 滑块——木板模型问题
一、滑块——木板的动力学问题
滑块-木板模型作为力学的基本模型经常出现,是对直线运动和牛顿运动定律有关知识的综合应用.着重考查学生分析问题、运用知识的能力,这类问题无论物体的运动情景如何复杂,这类问题的解答有一个基本技巧和方法:求解时应先仔细审题,清楚题目的含义,分析清楚每一个物体的受力情况、运动情况.因题目所给的情境中至少涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各运动过程中的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口.求解中更应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度.
【例1】 (2015云南玉溪一中期末)质量为、长为的长木板静止在光滑水平面上;质量也为的小滑块(可看做质点),放在长木板的左端,如图所示;给小滑块一水平向右的拉力;当取不同值时求解下列问题。(重力加速度为)
(1)使滑块在木板上发生相对滑动,至少为多大;
(2)当时,经多长时间,力可使滑块滑至木板的最右端;
(3)当时,至少作用多长时间后再撤去,最终滑块可以滑到木板的最右端。
二、图像在滑块——木板模型中的综合应用
首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”。
(1)“轴”:纵、横轴所表示的物理量,
(2)“线”:从线反映运动性质,
(3)“斜率”:“斜率”往往代表一个物理量
(4)“面”即“面积 ”:主要看纵、横轴物理量的乘积有无意义.
(5)“截距”:初始条件.
(6)“特殊值”:如交点、拐点。
滑块——木板模型中遇到带有物理图象的问题时,要认真分析图象,先从它的物理意义、点、线、斜率、面、截距、交点、拐点等方面了解图象给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式去解题。
【例2】(2015重庆一中期末)如图甲所示,质量为M=3.0kg的平板小车C静止在光滑的水平面上,在t=0时,两个质量均为1.0kg的小物体A和B同时从左右两端水平冲上小车,1.0s内它们的v-t图象如图乙所示,( g取10m/s2)求:
(1)小物体A和B与平板小车之间的动摩擦因数μA、μB
(2)判断小车在0~1.0s内所做的运动,并说明理由?
(3)要使A、B在整个运动过程中不会相碰,车的长度至少为多少?
课时训练
1.(2015吉林期末)如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到向右的拉力F的作用,长木板处于静止状态。已知木块与木板间的动摩擦因数为μ1 ,木板与地面间的动摩擦因数为μ2 ,以下几种说法正确的是( )
A.木板受到地面的摩擦力的大小一定是μ1mg
B.木板受到地面的摩擦力的大小一定是μ2(m+M)g
C.当F>μ2(m+M)g时,木板便会开始运动
D.无论怎样改变F的大小,木板都不可能运动
2.(2015沈阳二中期末)如图所示,小车板面上的物体质量为m=8kg,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N.现沿水平向左的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1m/s2,此后以1m/s2的加速度向左做匀加速直线运动.在此过程中,以下说法正确的是( )
A.当小车加速度(向左)为0.75m/s2时,物体不受摩擦力作用
B.小车以1m/s2的加速度(向左)做匀加速直线运动时,物体受到的摩擦力为8N
C.物体受到的摩擦力先减小后增大,先向右后向左
D.物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化
3.如图甲所示,静止在光滑水平面上的长木板B(长木板足够长)的左端放着小物块A.某时刻,A受到水平向右的外力F作用,F随时间t的变化规律如图乙所示,即F=kt,其中k为已知常数.若物体之间的滑动摩擦力Ff的大小等于最大静摩擦力,且A,B的质量相等,则下列图中可以定性地描述长木板B运动的vt图象的是( )
4.如图所示,在光滑的水平面上放着质量为M的木板,在木板的左端有一个质量为m的木块,在木块上施加一个水平向右的恒力F,木块与木板由静止开始运动,经过时间t分离.下列说法正确的是( )
A.若仅增大木板的质量M,则时间t增大
B.若仅增大木块的质量m,则时间t增大
C.若仅增大恒力F,则时间t增大
D.若仅增大木块与木板间的动摩擦因数,则时间t增大
5.(2011·课标全国卷) 如图所示,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( )
6.(2014·江苏卷)如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上.A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对A施加一水平拉力F,则( )
A.当F<2μmg 时,A、B都相对地面静止
B.当F=μmg时,A的加速度为μg
C.当F>3μmg时,A相对B滑动
D.无论F为何值,B的加速度不会超过μg
7.如图1,质量为M的长木板,静止放在粗糙的水平地面上,有一个质量为 m、可视为质点的物块,已某一水平初速度从左端冲上木板.从物块冲上木板到物块和木板都静止的过程中,物块和木板的图象分别如图2中的折线所示,根据图2,(g=10m/s2)求:
(1)m与M 间动摩擦因数μ1及M与地面间动摩擦因数μ2;
(2)m与M的质量之比;
(3)从物块冲上木板到物块和木板都静止的过程中,物块m、长木板M各自对地的位移.
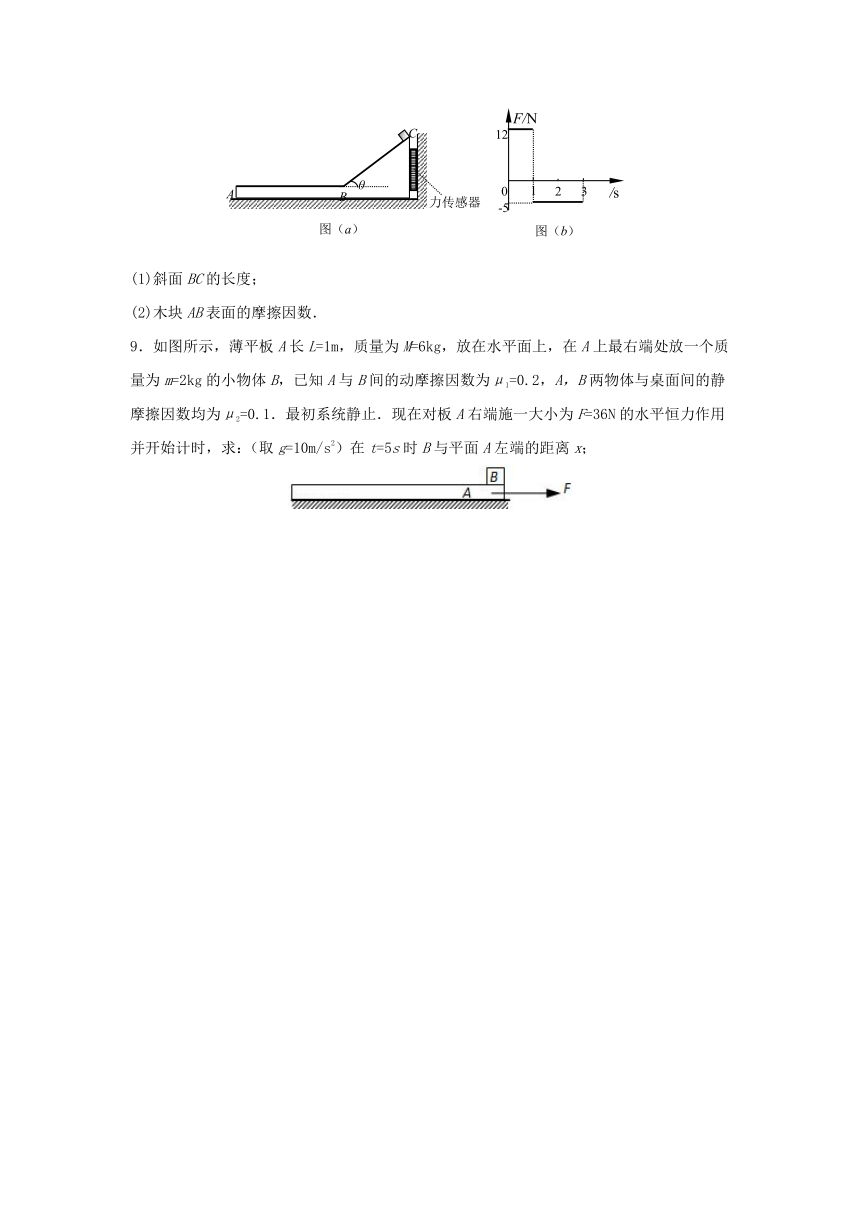
8.(2015沈阳二中期末)如图(a)所示,“”型木块放在光滑水平地面上,木块水平表面AB粗糙, BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)斜面BC的长度;
(2)木块AB表面的摩擦因数.
9.如图所示,薄平板A长L=1m,质量为M=6kg,放在水平面上,在A上最右端处放一个质量为m=2kg的小物体B,已知A与B间的动摩擦因数为μ1=0.2,A,B两物体与桌面间的静摩擦因数均为μ2=0.1.最初系统静止.现在对板A右端施一大小为F=36N的水平恒力作用并开始计时,求:(取g=10m/s2)在t=5s时B与平面A左端的距离x;
答案精析
【例1】
【答案】(1)(2)(3)
【解析】(1)对滑块、木板整体有:
当滑块与木板间摩擦力达最大静摩擦力时,对木板有:
联立解得:
(2)设滑块、木板的加速度分别为a1、a2;
由牛顿运动定律得:
解得:,;
设经t时间,滑块滑到木板的最右端;
解得:
(3)设经t1时间撤去外力F;撤去外力F后,滑块的加速度为a3;
解得:
设撤去外力F后,再经t2时间,滑块滑到木板最右端时恰好和木板有相同的速度。
则:
解得:
位移关系有:
解得:
【例2】
【答案】(1)0.3;(2)小车静止;(3)7.2m
【解析】 (1)由v-t图可知,在第1 s内,物体A、B的加速度大小相等,均为a=3.0 m/s2.
根据牛顿第二定律: f =μmg=ma 可得μA=μB=0.3
(2)物体A、B所受摩擦力大小均为Ff=ma=3.0 N,方向相反,
根据牛顿第三定律,车C受A、B的摩擦力也大小相等,方向相反,合力为零,故小车静止。
(3)由图像可知0-1.0s内A的位移xA=4.5m B 的位移xB=1.5m
B减速到零后,对A f A=μmg=maA 解得aA=3m/s2
对B和车 f A=μmg=(M+m)aB 解得aB=0.75m/s2
设经过时间t,达到相同速度v
解得:t=0.8s v=0.6m/s
相对位移m
A、B之间的相对位移,即车的最小长度为:x=xA+xB+=7.2m
课时训练
1.【答案】AD
【解析】m在M表面上滑行,所以木块受到滑动摩擦力μ1mg,方向向左,因此木板受到滑动摩擦力向右,大小也为μ1mg。由于木板静止,所以地面给木板的静摩擦力大小为μ1mg,方向向左,A正确、B错误;不管F多大,木板受到滑动摩擦力为μ1mg,木板都不可能运动,C错误、D正确。
2.【答案】ACD
【解析】当小车加速度(向左)为0.75m/s2时,物体所受的合力为6N,物体不受摩擦力作用,A正确;小车以1m/s2的加速度(向左)做匀加速直线运动时,物体受到的合力为8N,则物体受到的摩擦力为2N,B错误;由以上分析知,物体受到的摩擦力先向右由6N减小到零后向左增加到2N,C正确;由题中条件,小车静止时,物体受到的摩擦力为6N,可知物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化,D正确。
3.【答案】B
【解析】在A,B相对滑动前,对A,B整体由牛顿第二定律得a==,故A,B的加速度随时间的增大而增大,速度时间图象是一向上弯曲的曲线;A相对B刚好要滑动时,对B由牛顿第二定律得a=,由于=,故t=;在A相对B滑动后,B的加速度a=为一恒量,速度时间图象是一倾斜向上的直线,故B正确.
4.【答案】BD
【解析】设木块与木板间的动摩擦因数为μ,则木块的加速度a1==-μg,木板的加速度a2=,两者恰好分离的条件为 (a1-a2)t2=L,时间t=.由此可知,仅增大M或F,时间t减小,仅增大m或μ,时间t增大,选项B,D正确.
5.【答案】A
【解析】当拉力F很小时,木块和木板一起加速运动,由牛顿第二定律,对木块和木板:F=(m1+m2)a,故a1=a2=a==;当拉力很大时,木块和木板将发生相对运动,对木板:μm2g=m1a1,得a1=,对木块:F-μm2g=m1a2,得a2==t-μg,A正确.
6.【答案】BCD
【解析】设B对A的摩擦力为f1,A对B的摩擦力为f2,地面对B的摩擦力为f3,由牛顿第三定律可知f1与f2大小相等,方向相反,f1和f2的最大值均为2μmg,f3的最大值为μmg.故当03μmg时,A相对于B滑动.由以上分析可知A错误,C正确.当F=μmg时,A、B以共同的加速度开始运动,将A、B看作整体,由牛顿第二定律有F-μmg=3ma,解得a=,B正确.对B来说,其所受合力的最大值Fm=2μmg-μmg=μmg,即B的加速度不会超过μg,D正确.
7.【答案】(1)m与M 间动摩擦因数μ1及M与地面间动摩擦因数μ2分别为0.15,0.05.
(2)m与M的质量之比为3:2.
(3)从物块冲上木板到物块和木板都静止的过程中,物块m、长木板M各自对地的位移分别为44m,24m.
【解析】(1)由图可知.ac为m 的速度图象.m的加速度为:
根据牛顿第二定律得:μ1mg=ma1
所以得:
由图可知cd为二者一起减速运动的图象,其加速度为:
又a3=μ2g,解得:
(2)对bc段,对M写动力学方程:
μ1mg﹣μ2(mg+Mg)=Ma2
由bc图可知:
把 μ1、μ2 代入上式,可得:
(3)图象acd与横轴所围面积可求m对地位移为:
图象bcd与横轴所围面积可求M对地位移为:
8.【答案】(1)3m (2)0.2
【解析】试题分析:⑴分析滑块受力,
由牛顿第二定律得:,通过图像可知滑块在斜面上运动的时间为:,由运动学公式得:=3m
⑵滑块对斜面的压力为: 木块对传感器的压力为:
由图像可知:F1=12N,解得:m=2.5Kg 传感器对木板的拉力 N,解得:μ=0.2
9.【答案】在t=5s时B与平面A左端的距离是54m;
【解析】对B而言,μ1mg=ma1得:
对A:F﹣μ1mg﹣μ2(M+m)g=Ma2
代入数据得:
设分离是时间是t1,则:;
又:x2﹣x1=L
代入数据解得:t1=1s ;x2=2m
分离时A的速度:vA=a2t1=4×1m/s=4m/s
分离时B的速度:vB=a1t1=2×1m/s=2m/s
分离后B的加速度:
B减速到0的时间:
所以:m
分离后A 的加速度:
分离后A的位移:代入数据得:xA=56m
在t=5s时B与平面A左端的距离:x=xA﹣xB=56﹣2=54m
图(a)
A
θ
B
C
力传感器
0
F/N
/s
-5
12
1
2
3
图(b)
一、滑块——木板的动力学问题
滑块-木板模型作为力学的基本模型经常出现,是对直线运动和牛顿运动定律有关知识的综合应用.着重考查学生分析问题、运用知识的能力,这类问题无论物体的运动情景如何复杂,这类问题的解答有一个基本技巧和方法:求解时应先仔细审题,清楚题目的含义,分析清楚每一个物体的受力情况、运动情况.因题目所给的情境中至少涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各运动过程中的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口.求解中更应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度.
【例1】 (2015云南玉溪一中期末)质量为、长为的长木板静止在光滑水平面上;质量也为的小滑块(可看做质点),放在长木板的左端,如图所示;给小滑块一水平向右的拉力;当取不同值时求解下列问题。(重力加速度为)
(1)使滑块在木板上发生相对滑动,至少为多大;
(2)当时,经多长时间,力可使滑块滑至木板的最右端;
(3)当时,至少作用多长时间后再撤去,最终滑块可以滑到木板的最右端。
二、图像在滑块——木板模型中的综合应用
首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”。
(1)“轴”:纵、横轴所表示的物理量,
(2)“线”:从线反映运动性质,
(3)“斜率”:“斜率”往往代表一个物理量
(4)“面”即“面积 ”:主要看纵、横轴物理量的乘积有无意义.
(5)“截距”:初始条件.
(6)“特殊值”:如交点、拐点。
滑块——木板模型中遇到带有物理图象的问题时,要认真分析图象,先从它的物理意义、点、线、斜率、面、截距、交点、拐点等方面了解图象给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式去解题。
【例2】(2015重庆一中期末)如图甲所示,质量为M=3.0kg的平板小车C静止在光滑的水平面上,在t=0时,两个质量均为1.0kg的小物体A和B同时从左右两端水平冲上小车,1.0s内它们的v-t图象如图乙所示,( g取10m/s2)求:
(1)小物体A和B与平板小车之间的动摩擦因数μA、μB
(2)判断小车在0~1.0s内所做的运动,并说明理由?
(3)要使A、B在整个运动过程中不会相碰,车的长度至少为多少?
课时训练
1.(2015吉林期末)如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到向右的拉力F的作用,长木板处于静止状态。已知木块与木板间的动摩擦因数为μ1 ,木板与地面间的动摩擦因数为μ2 ,以下几种说法正确的是( )
A.木板受到地面的摩擦力的大小一定是μ1mg
B.木板受到地面的摩擦力的大小一定是μ2(m+M)g
C.当F>μ2(m+M)g时,木板便会开始运动
D.无论怎样改变F的大小,木板都不可能运动
2.(2015沈阳二中期末)如图所示,小车板面上的物体质量为m=8kg,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N.现沿水平向左的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1m/s2,此后以1m/s2的加速度向左做匀加速直线运动.在此过程中,以下说法正确的是( )
A.当小车加速度(向左)为0.75m/s2时,物体不受摩擦力作用
B.小车以1m/s2的加速度(向左)做匀加速直线运动时,物体受到的摩擦力为8N
C.物体受到的摩擦力先减小后增大,先向右后向左
D.物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化
3.如图甲所示,静止在光滑水平面上的长木板B(长木板足够长)的左端放着小物块A.某时刻,A受到水平向右的外力F作用,F随时间t的变化规律如图乙所示,即F=kt,其中k为已知常数.若物体之间的滑动摩擦力Ff的大小等于最大静摩擦力,且A,B的质量相等,则下列图中可以定性地描述长木板B运动的vt图象的是( )
4.如图所示,在光滑的水平面上放着质量为M的木板,在木板的左端有一个质量为m的木块,在木块上施加一个水平向右的恒力F,木块与木板由静止开始运动,经过时间t分离.下列说法正确的是( )
A.若仅增大木板的质量M,则时间t增大
B.若仅增大木块的质量m,则时间t增大
C.若仅增大恒力F,则时间t增大
D.若仅增大木块与木板间的动摩擦因数,则时间t增大
5.(2011·课标全国卷) 如图所示,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( )
6.(2014·江苏卷)如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上.A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对A施加一水平拉力F,则( )
A.当F<2μmg 时,A、B都相对地面静止
B.当F=μmg时,A的加速度为μg
C.当F>3μmg时,A相对B滑动
D.无论F为何值,B的加速度不会超过μg
7.如图1,质量为M的长木板,静止放在粗糙的水平地面上,有一个质量为 m、可视为质点的物块,已某一水平初速度从左端冲上木板.从物块冲上木板到物块和木板都静止的过程中,物块和木板的图象分别如图2中的折线所示,根据图2,(g=10m/s2)求:
(1)m与M 间动摩擦因数μ1及M与地面间动摩擦因数μ2;
(2)m与M的质量之比;
(3)从物块冲上木板到物块和木板都静止的过程中,物块m、长木板M各自对地的位移.
8.(2015沈阳二中期末)如图(a)所示,“”型木块放在光滑水平地面上,木块水平表面AB粗糙, BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)斜面BC的长度;
(2)木块AB表面的摩擦因数.
9.如图所示,薄平板A长L=1m,质量为M=6kg,放在水平面上,在A上最右端处放一个质量为m=2kg的小物体B,已知A与B间的动摩擦因数为μ1=0.2,A,B两物体与桌面间的静摩擦因数均为μ2=0.1.最初系统静止.现在对板A右端施一大小为F=36N的水平恒力作用并开始计时,求:(取g=10m/s2)在t=5s时B与平面A左端的距离x;
答案精析
【例1】
【答案】(1)(2)(3)
【解析】(1)对滑块、木板整体有:
当滑块与木板间摩擦力达最大静摩擦力时,对木板有:
联立解得:
(2)设滑块、木板的加速度分别为a1、a2;
由牛顿运动定律得:
解得:,;
设经t时间,滑块滑到木板的最右端;
解得:
(3)设经t1时间撤去外力F;撤去外力F后,滑块的加速度为a3;
解得:
设撤去外力F后,再经t2时间,滑块滑到木板最右端时恰好和木板有相同的速度。
则:
解得:
位移关系有:
解得:
【例2】
【答案】(1)0.3;(2)小车静止;(3)7.2m
【解析】 (1)由v-t图可知,在第1 s内,物体A、B的加速度大小相等,均为a=3.0 m/s2.
根据牛顿第二定律: f =μmg=ma 可得μA=μB=0.3
(2)物体A、B所受摩擦力大小均为Ff=ma=3.0 N,方向相反,
根据牛顿第三定律,车C受A、B的摩擦力也大小相等,方向相反,合力为零,故小车静止。
(3)由图像可知0-1.0s内A的位移xA=4.5m B 的位移xB=1.5m
B减速到零后,对A f A=μmg=maA 解得aA=3m/s2
对B和车 f A=μmg=(M+m)aB 解得aB=0.75m/s2
设经过时间t,达到相同速度v
解得:t=0.8s v=0.6m/s
相对位移m
A、B之间的相对位移,即车的最小长度为:x=xA+xB+=7.2m
课时训练
1.【答案】AD
【解析】m在M表面上滑行,所以木块受到滑动摩擦力μ1mg,方向向左,因此木板受到滑动摩擦力向右,大小也为μ1mg。由于木板静止,所以地面给木板的静摩擦力大小为μ1mg,方向向左,A正确、B错误;不管F多大,木板受到滑动摩擦力为μ1mg,木板都不可能运动,C错误、D正确。
2.【答案】ACD
【解析】当小车加速度(向左)为0.75m/s2时,物体所受的合力为6N,物体不受摩擦力作用,A正确;小车以1m/s2的加速度(向左)做匀加速直线运动时,物体受到的合力为8N,则物体受到的摩擦力为2N,B错误;由以上分析知,物体受到的摩擦力先向右由6N减小到零后向左增加到2N,C正确;由题中条件,小车静止时,物体受到的摩擦力为6N,可知物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化,D正确。
3.【答案】B
【解析】在A,B相对滑动前,对A,B整体由牛顿第二定律得a==,故A,B的加速度随时间的增大而增大,速度时间图象是一向上弯曲的曲线;A相对B刚好要滑动时,对B由牛顿第二定律得a=,由于=,故t=;在A相对B滑动后,B的加速度a=为一恒量,速度时间图象是一倾斜向上的直线,故B正确.
4.【答案】BD
【解析】设木块与木板间的动摩擦因数为μ,则木块的加速度a1==-μg,木板的加速度a2=,两者恰好分离的条件为 (a1-a2)t2=L,时间t=.由此可知,仅增大M或F,时间t减小,仅增大m或μ,时间t增大,选项B,D正确.
5.【答案】A
【解析】当拉力F很小时,木块和木板一起加速运动,由牛顿第二定律,对木块和木板:F=(m1+m2)a,故a1=a2=a==;当拉力很大时,木块和木板将发生相对运动,对木板:μm2g=m1a1,得a1=,对木块:F-μm2g=m1a2,得a2==t-μg,A正确.
6.【答案】BCD
【解析】设B对A的摩擦力为f1,A对B的摩擦力为f2,地面对B的摩擦力为f3,由牛顿第三定律可知f1与f2大小相等,方向相反,f1和f2的最大值均为2μmg,f3的最大值为μmg.故当0
7.【答案】(1)m与M 间动摩擦因数μ1及M与地面间动摩擦因数μ2分别为0.15,0.05.
(2)m与M的质量之比为3:2.
(3)从物块冲上木板到物块和木板都静止的过程中,物块m、长木板M各自对地的位移分别为44m,24m.
【解析】(1)由图可知.ac为m 的速度图象.m的加速度为:
根据牛顿第二定律得:μ1mg=ma1
所以得:
由图可知cd为二者一起减速运动的图象,其加速度为:
又a3=μ2g,解得:
(2)对bc段,对M写动力学方程:
μ1mg﹣μ2(mg+Mg)=Ma2
由bc图可知:
把 μ1、μ2 代入上式,可得:
(3)图象acd与横轴所围面积可求m对地位移为:
图象bcd与横轴所围面积可求M对地位移为:
8.【答案】(1)3m (2)0.2
【解析】试题分析:⑴分析滑块受力,
由牛顿第二定律得:,通过图像可知滑块在斜面上运动的时间为:,由运动学公式得:=3m
⑵滑块对斜面的压力为: 木块对传感器的压力为:
由图像可知:F1=12N,解得:m=2.5Kg 传感器对木板的拉力 N,解得:μ=0.2
9.【答案】在t=5s时B与平面A左端的距离是54m;
【解析】对B而言,μ1mg=ma1得:
对A:F﹣μ1mg﹣μ2(M+m)g=Ma2
代入数据得:
设分离是时间是t1,则:;
又:x2﹣x1=L
代入数据解得:t1=1s ;x2=2m
分离时A的速度:vA=a2t1=4×1m/s=4m/s
分离时B的速度:vB=a1t1=2×1m/s=2m/s
分离后B的加速度:
B减速到0的时间:
所以:m
分离后A 的加速度:
分离后A的位移:代入数据得:xA=56m
在t=5s时B与平面A左端的距离:x=xA﹣xB=56﹣2=54m
图(a)
A
θ
B
C
力传感器
0
F/N
/s
-5
12
1
2
3
图(b)
同课章节目录
