湘教版九年级数学上册第三章 图形的相似 相似多边形(修改版)
文档属性
| 名称 | 湘教版九年级数学上册第三章 图形的相似 相似多边形(修改版) |
|
|
| 格式 | rar | ||
| 文件大小 | 16.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-17 00:00:00 | ||
图片预览

文档简介
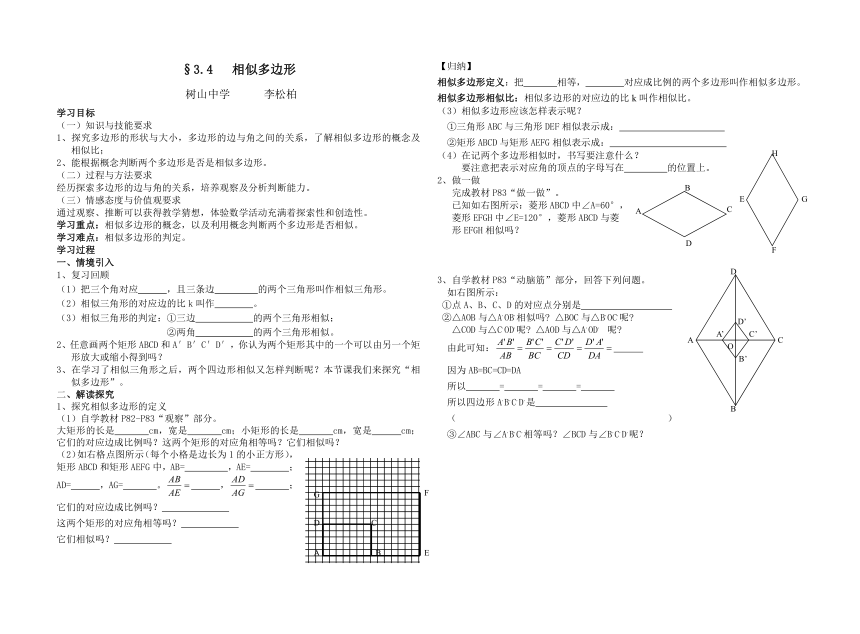
§3.4 相似多边形
树山中学 李松柏
学习目标
(一)知识与技能要求
1、探究多边形的形状与大小,多边形的边与角之间的关系,了解相似多边形的概念及相似比;
2、能根据概念判断两个多边形是否是相似多边形。
(二)过程与方法要求
经历探索多边形的边与角的关系,培养观察及分析判断能力。
(三)情感态度与价值观要求
通过观察、推断可以获得教学猜想,体验数学活动充满着探索性和创造性。
学习重点:相似多边形的概念,以及利用概念判断两个多边形是否相似。
学习难点:相似多边形的判定。
学习过程
一、情境引入
1、复习回顾
(1)把三个角对应 ,且三条边 的两个三角形叫作相似三角形。
(2)相似三角形的对应边的比k叫作 。
(3)相似三角形的判定:①三边 的两个三角形相似;
②两角 的两个三角形相似。
2、任意画两个矩形ABCD和A′B′C′D′,你认为两个矩形其中的一个可以由另一个矩形放大或缩小得到吗?
3、在学习了相似三角形之后,两个四边形相似又怎样判断呢?本节课我们来探究“相似多边形”。
二、解读探究
1、探究相似多边形的定义
(1)自学教材P82-P83“观察”部分。
大矩形的长是 cm,宽是 cm;小矩形的长是 cm,宽是 cm;它们的对应边成比例吗?这两个矩形的对应角相等吗?它们相似吗?
(2)如右格点图所示(每个小格是边长为1的小正方形),
矩形ABCD和矩形AEFG中,AB= ,AE= ;
AD= ,AG= 。 , ;
它们的对应边成比例吗?
这两个矩形的对应角相等吗?
它们相似吗?
【归纳】
相似多边形定义:把 相等, 对应成比例的两个多边形叫作相似多边形。
相似多边形相似比:相似多边形的对应边的比k叫作相似比。
(3)相似多边形应该怎样表示呢?
①三角形ABC与三角形DEF相似表示成:
②矩形ABCD与矩形AEFG相似表示成:
(4)在记两个多边形相似时,书写要注意什么?
要注意把表示对应角的顶点的字母写在 的位置上。
2、做一做
完成教材P83“做一做”。
已知如右图所示:菱形ABCD中∠A=60°,
菱形EFGH中∠E=120°,菱形ABCD与菱
形EFGH相似吗?
3、自学教材P83“动脑筋”部分,回答下列问题。
如右图所示:
①点A、B、C、D的对应点分别是
②△AOB与△A,OB,相似吗 △BOC与△B,OC,呢
△COD与△C,OD,呢 △AOD与△A,OD, 呢
由此可知:
因为AB=BC=CD=DA
所以 = = =
所以四边形A,B,C,D,是
( )
③∠ABC与∠A,B,C,相等吗?∠BCD与∠B,C,D,呢?
∠CDA与∠C,D,A,呢?∠DAB与∠D,A,B呢?与同伴交流。
综合②和③,我们知道菱形A,B,C,D,与菱形ABCD ,记作
三、应用巩固
1、任意两个正方形相似吗? 2、邻边不相等的矩形与正方形相似吗?
四、总结提升
1、本节课你学会了什么?
本节课我们通过探究满足多边形相似的条件,从而推导出相似多边形的定义,并能根据定义判断某些多边形是否为相似多边形。
2、你还有哪些疑问呢?
五、作业训练(A类课堂完成)
A类
1、下列多边形哪些是相似的?
2、如图,梯形ABCD的两条对角线相交于点O,在AO、BO、CO、DO上分别取一点E、F、G、H,使得,
①求证:梯形ABCD∽梯形EFGH;
②求梯形ABCD与梯形EFGH的相似比。
B类
1、如图所示,有一块矩形草地,其外围有等宽的小路,其中草地长100m、宽60m,小路宽2m,里外两个矩形相似吗?
2、如图,已知梯形ABCD中,AD∥BC,AD=15,BC=30,点E、F分别为AB、CD上的点,且EF∥BC,若梯形AEFD∽EBCF,求线段EF的长。
3、一个矩形减去一个宽为边长的正方形以后所剩下的矩形与原来的矩形相似,则原来的矩形宽与长之比是多少?
六、预习提示(P84 “探究”)
1、相似多边形的周长的比与相似比有什么关系?
2、相似多边形的面积的比与相似比有什么关系?
B′
A′
D
C
B
A
G
F
E
H
D
C
B
A
正方形
G
矩形
E
A
平行四边形
A
菱形
C
正八边形
N
正六边形
K
菱形
D
正六边形
L
等腰梯形
J
正八边形
M
正方形
H
平行四边形
B
等腰梯形
I
矩形
F
B
C
D
E
H
G
F
O
E
F
D
C
B
C′
G
A
D′
A
D
C
BB
E
F
A
D
C
B
F
E
草地
AA
DA
CA
BA
A’A
C’A
D’A
B’A
正方形
A
正方形
B
矩形
A
正方形
B
O
树山中学 李松柏
学习目标
(一)知识与技能要求
1、探究多边形的形状与大小,多边形的边与角之间的关系,了解相似多边形的概念及相似比;
2、能根据概念判断两个多边形是否是相似多边形。
(二)过程与方法要求
经历探索多边形的边与角的关系,培养观察及分析判断能力。
(三)情感态度与价值观要求
通过观察、推断可以获得教学猜想,体验数学活动充满着探索性和创造性。
学习重点:相似多边形的概念,以及利用概念判断两个多边形是否相似。
学习难点:相似多边形的判定。
学习过程
一、情境引入
1、复习回顾
(1)把三个角对应 ,且三条边 的两个三角形叫作相似三角形。
(2)相似三角形的对应边的比k叫作 。
(3)相似三角形的判定:①三边 的两个三角形相似;
②两角 的两个三角形相似。
2、任意画两个矩形ABCD和A′B′C′D′,你认为两个矩形其中的一个可以由另一个矩形放大或缩小得到吗?
3、在学习了相似三角形之后,两个四边形相似又怎样判断呢?本节课我们来探究“相似多边形”。
二、解读探究
1、探究相似多边形的定义
(1)自学教材P82-P83“观察”部分。
大矩形的长是 cm,宽是 cm;小矩形的长是 cm,宽是 cm;它们的对应边成比例吗?这两个矩形的对应角相等吗?它们相似吗?
(2)如右格点图所示(每个小格是边长为1的小正方形),
矩形ABCD和矩形AEFG中,AB= ,AE= ;
AD= ,AG= 。 , ;
它们的对应边成比例吗?
这两个矩形的对应角相等吗?
它们相似吗?
【归纳】
相似多边形定义:把 相等, 对应成比例的两个多边形叫作相似多边形。
相似多边形相似比:相似多边形的对应边的比k叫作相似比。
(3)相似多边形应该怎样表示呢?
①三角形ABC与三角形DEF相似表示成:
②矩形ABCD与矩形AEFG相似表示成:
(4)在记两个多边形相似时,书写要注意什么?
要注意把表示对应角的顶点的字母写在 的位置上。
2、做一做
完成教材P83“做一做”。
已知如右图所示:菱形ABCD中∠A=60°,
菱形EFGH中∠E=120°,菱形ABCD与菱
形EFGH相似吗?
3、自学教材P83“动脑筋”部分,回答下列问题。
如右图所示:
①点A、B、C、D的对应点分别是
②△AOB与△A,OB,相似吗 △BOC与△B,OC,呢
△COD与△C,OD,呢 △AOD与△A,OD, 呢
由此可知:
因为AB=BC=CD=DA
所以 = = =
所以四边形A,B,C,D,是
( )
③∠ABC与∠A,B,C,相等吗?∠BCD与∠B,C,D,呢?
∠CDA与∠C,D,A,呢?∠DAB与∠D,A,B呢?与同伴交流。
综合②和③,我们知道菱形A,B,C,D,与菱形ABCD ,记作
三、应用巩固
1、任意两个正方形相似吗? 2、邻边不相等的矩形与正方形相似吗?
四、总结提升
1、本节课你学会了什么?
本节课我们通过探究满足多边形相似的条件,从而推导出相似多边形的定义,并能根据定义判断某些多边形是否为相似多边形。
2、你还有哪些疑问呢?
五、作业训练(A类课堂完成)
A类
1、下列多边形哪些是相似的?
2、如图,梯形ABCD的两条对角线相交于点O,在AO、BO、CO、DO上分别取一点E、F、G、H,使得,
①求证:梯形ABCD∽梯形EFGH;
②求梯形ABCD与梯形EFGH的相似比。
B类
1、如图所示,有一块矩形草地,其外围有等宽的小路,其中草地长100m、宽60m,小路宽2m,里外两个矩形相似吗?
2、如图,已知梯形ABCD中,AD∥BC,AD=15,BC=30,点E、F分别为AB、CD上的点,且EF∥BC,若梯形AEFD∽EBCF,求线段EF的长。
3、一个矩形减去一个宽为边长的正方形以后所剩下的矩形与原来的矩形相似,则原来的矩形宽与长之比是多少?
六、预习提示(P84 “探究”)
1、相似多边形的周长的比与相似比有什么关系?
2、相似多边形的面积的比与相似比有什么关系?
B′
A′
D
C
B
A
G
F
E
H
D
C
B
A
正方形
G
矩形
E
A
平行四边形
A
菱形
C
正八边形
N
正六边形
K
菱形
D
正六边形
L
等腰梯形
J
正八边形
M
正方形
H
平行四边形
B
等腰梯形
I
矩形
F
B
C
D
E
H
G
F
O
E
F
D
C
B
C′
G
A
D′
A
D
C
BB
E
F
A
D
C
B
F
E
草地
AA
DA
CA
BA
A’A
C’A
D’A
B’A
正方形
A
正方形
B
矩形
A
正方形
B
O
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
