人教版数学九上 第二十二章 二次函数 单元练习(含答案)
文档属性
| 名称 | 人教版数学九上 第二十二章 二次函数 单元练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 278.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 11:49:59 | ||
图片预览




文档简介
人教版数学九上二次函数
一、单选题
1.下列函数关系中,y是x的二次函数的是( )
A. B.
C. D.
2.若点 , , ,都在函数 的图象上,则( )
A. B. C. D.
3.将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为( )
A. B.
C. D.
4.已知函数 的图象与x轴有交点.则 的取值范围是( )
A.k<4 B.k≤4 C.k<4且k≠3 D.k≤4且k≠3
5.根据表格中二次函数的自变量与函数值的对应值,可以判断方程的一个解的范围是( )
0 0.5 1 1.5 2
-1 -0.5 1 3.5 7
A. B. C. D.
6.二次函数 的图象如图所示,对称轴为直线 ,下列结论不正确的是( )
A.
B.当 时,顶点的坐标为
C.当 时,
D.当 时,y随x的增大而增大
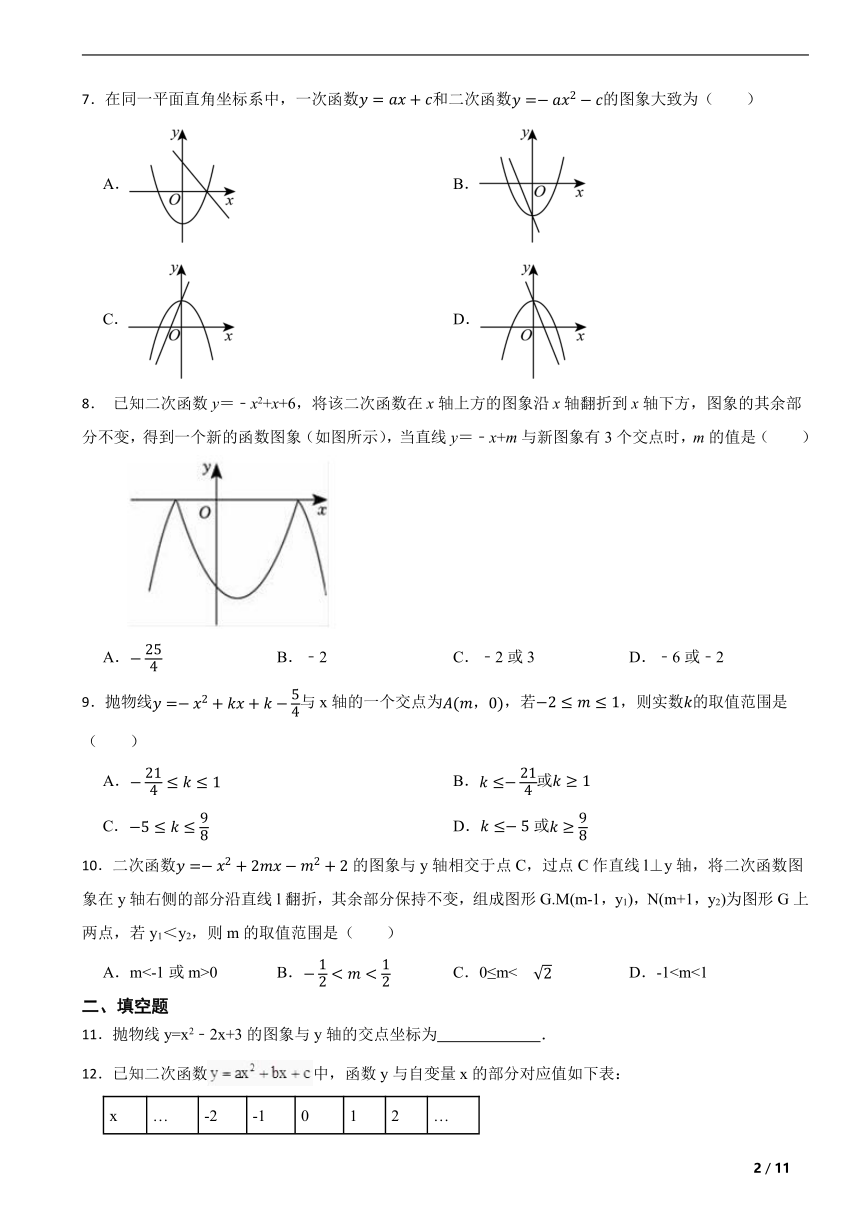
7.在同一平面直角坐标系中,一次函数和二次函数的图象大致为( )
A. B.
C. D.
8. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( )
A. B.﹣2 C.﹣2或3 D.﹣6或﹣2
9.抛物线与x轴的一个交点为,若,则实数的取值范围是( )
A. B.或
C. D.或
10.二次函数的图象与y轴相交于点C,过点C作直线l⊥y轴,将二次函数图象在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.M(m-1,y1),N(m+1,y2)为图形G上两点,若y1<y2,则m的取值范围是( )
A.m<-1或m>0 B. C.0≤m< D.-1二、填空题
11.抛物线y=x2﹣2x+3的图象与y轴的交点坐标为 .
12.已知二次函数中,函数y与自变量x的部分对应值如下表:
x … -2 -1 0 1 2 …
y … -3 -4 -3 0 5 …
则此二次函数的对称轴为
13.点在第二象限内,点,则的取值范围是 .
14.已知二次函数 的图象与x轴没有公共点,且当 时,y随x的增大而减小,则实数a的取值范围是 .
15. 关于的二次函数,在时有最大值6,则 .
16.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(4,4),小车沿抛物线y=ax2﹣2ax﹣3a(a<0)运动.若小车在运动过程中只触发一次报警装置,则a的取值范围是 .
三、解答题
17.已知函数 (为常数).
(1)求当为何值时是的二次函数?
(2)在()的条件下,点在此函数图象上,求的值.
18.已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
19.杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体看成一点的路线是抛物线的一部分,如图所示.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
20. 如图,在平面直角坐标系中,直线分别交x轴,y轴于A,B两点.抛物线经过A,B两点,且与x轴的另一个交点为.
(1)求该抛物线的解析式.
(2)若点P是线段AB上一个动点,过点P作x轴的垂线,交该抛物线于点Q,连接AQ,BQ,求面积的最大值.
21.阅读理解:
某“数学兴趣小组”根据学习函数的经验,对函数的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
… …
… …
其中 ;
(2)在平面直角坐标系中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)根据函数图象,回答下列问题:
①当时,则y的取值范围为 .
②直线经过点,若关于x的方程有4个互不相等的实数根,则b的取值范围是 .
22.已知二次函数.
(1)当时,
①求该函数图象向顶点坐标.
②当时,求的取值范围.
(2)当时,的最大值为2;当时,的最大值为3,求二次函数的表达式.
23.问题提出:
四边形是正方形,是射线上的动点,点在线段的延长线上,且,连接,将线段绕点顺时针旋转得到,连接,设,四边形的面积为(可等于0).
(1)如图①,当点由点运动到点过程中,发现是关于的二次函数,并绘制成如图②所示的图象,抛物线经过原点且顶点为,请根据图象信息,回答下列问题:
①正方形的边长为___________(直接填空);
②求关于的函数关系式;
(2)如图③,当点在线段的延长线上运动时,求关于的函数关系式;
(3)若在射线上从下至上依次存在不同位置的两个点,对应的四边形的面积与四边形的面积相等,当时,求四边形的面积.
参考答案
1.C
2.C
3.A
4.B
5.B
6.C
7.A
8.D
解:如图所示:当直线y=﹣x+m与新图象有3个交点时,会有①②两种情况:
∵二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,
∴ 其与x轴的交点A(-2,0),下翻的图象解析式y=x2-x-6
当直线y=﹣x+m与新图象有3个交点时,此时直线过点A(-2,0)
∴ -(-2)+m=0
∴ m=-2
当直线y=﹣x+m与新图象有3个交点时,此时直线与下翻的图象解析式y=x2-x-6只有1个交点
∴ x2-x-6=-x+m
∴x2-6-m=0
∴=-4(-6-m)=0
解得m=-6
综上,当直线y=﹣x+m与新图象有3个交点时,m的值是-6或-2
9.B
解:∵与x轴的一个交点为,
∴存在实数根,
∴,
解得,
当k≤-5时,画出图像如图所示:
∴当x=-2时,,
解得,
当k≥1时,画出图像如图所示:
当x=-2时,,
解得,
∴,
10.D
解:在y=-x2+2mx-m2+2中,当x=m-1时,y=-(m-1)2+2m(m-1)-m2+2=1,
当x=m+1时,y=-(m+1)2+2m(m+1)-m2+2=1,
∴(m-1,1)和(m+1,1)是关于抛物线y=-x2+2mx-m2+2对称轴对称的两点,
若m-1≥0,即(m-1,1)和(m+1,1)在y轴右侧或(m-1,1)在y轴上,(m+1,1)在y轴右侧,
则点(m-1,1)经过翻折得M(m-1,y1),点(m+1,1)经过翻折得N(m+1,y2),
如图:
由对称性可知,y1=y2,
∴此时不满足y1<y2;
若m+1≤0,即(m-1,1)和(m+1,1)在y轴左侧或(m+1,1)在y轴上,(m-1,1)在y轴左侧,
则点(m-1,1)即为M(m-1,y1),点(m+1,1)即为N(m+1,y2),
∴y1=y2,
∴此时不满足y1<y2;
若m-1<0<m+1,即(m-1,1)在y轴左侧,(m+1,1)在y轴右侧时,如图:
此时M(m-1,1),(m+1,1)翻折后得N,满足y1<y2;
∵m-1<0<m+1,
解得:-1<m<1,
故答案为:D
11.(0,3)
12.x=-1
13.
14.-1≤a<2
解:由题意得:△ ,解得 ,
,故抛物线开口向上,对称轴为x=a
当 时, 随 的增大而减小,则 ,
实数 的取值范围是-1≤a<2.
15.2或
解:y=ax2+a2,
①当a>0时,二次函数的对称轴为x=0,
∴x=-1时,ymax=a+a2=6,
解得:a=2或a=-3(舍去);
②当a<0时,二次函数的对称轴为x=0,
∴x=0时,ymax=a2=6,
解得:a=或a=(舍去),
综上所述,a=2或.
16.a=﹣1或a<﹣ 或a>
解:抛物线y=ax2﹣2ax﹣3a=a(x+1)(x﹣3),
∴其对称轴为:x=1,且图象与x轴交于(﹣1,0),(3,0).
∵抛物线顶点为(1,﹣4a),当顶点在线段AB上时,﹣4a=4,则a=﹣1;
当抛物线过点(0,4)时,代入解析式得4=﹣3a,∴a=﹣ ,
由对称轴为x=1及图象与x轴交于(﹣1,0),(3,0)可知,当a<﹣ 时,抛物线与线段AB只有一个交点;
当抛物线过点(4,4)时,代入解析式得16a﹣8a﹣3a=4,
∴a= ,同理可知当a> 时,抛物线与线段AB只有一个交点.
17.(1);
(2)
18.(1)y=﹣x2﹣2x+3;(2)点P(﹣2,3)在这个二次函数的图象上,
19.(1)解:根据题意可知,抛物线方程为 ,可知二次项系数a=-,a<0,抛物线图像开口向下,所以存在最大值,
对抛物线方程为 ,进行化简得:
y=-+,
可知当x=时,抛物线对应的值最大,最大值为:
因此演员弹跳的最大高度是米.
(2)解:当x=4时,y=-×42+3×4+1=3.4=BC,
所以这次表演成功.
20.(1)抛物线解析式为:
(2)解:如图,设点P的横坐标为m,则,,
∴,
∵,
∴,
∵,
∴当时,面积的最大值为
21.(1)1
(2)解:根据表格:
… …
… …
描点法作出函数的图象如下图所示:
(3);
22.(1)解:①顶点坐标为(2,7).
②当-1≤x≤3时,-2≤y≤7.
(2)解:∵当x≤0时,y的最大值为2;当x>0时,y的最大值为3,
∴抛物线的对称轴在y轴的右侧,b>0.
∵抛物线开口向下,当x≤0时,y的最大值为2,∴c=2,
又∵当x>0时,y的最大值为3,∴,
∴b=±2.
∵b>0,
∴b=2.
∴二次函数的表达为y=-x2+2x+2.
23.(1)①4; ②
(2);
(3)四边形的面积为3或.
1 / 1
一、单选题
1.下列函数关系中,y是x的二次函数的是( )
A. B.
C. D.
2.若点 , , ,都在函数 的图象上,则( )
A. B. C. D.
3.将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为( )
A. B.
C. D.
4.已知函数 的图象与x轴有交点.则 的取值范围是( )
A.k<4 B.k≤4 C.k<4且k≠3 D.k≤4且k≠3
5.根据表格中二次函数的自变量与函数值的对应值,可以判断方程的一个解的范围是( )
0 0.5 1 1.5 2
-1 -0.5 1 3.5 7
A. B. C. D.
6.二次函数 的图象如图所示,对称轴为直线 ,下列结论不正确的是( )
A.
B.当 时,顶点的坐标为
C.当 时,
D.当 时,y随x的增大而增大
7.在同一平面直角坐标系中,一次函数和二次函数的图象大致为( )
A. B.
C. D.
8. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( )
A. B.﹣2 C.﹣2或3 D.﹣6或﹣2
9.抛物线与x轴的一个交点为,若,则实数的取值范围是( )
A. B.或
C. D.或
10.二次函数的图象与y轴相交于点C,过点C作直线l⊥y轴,将二次函数图象在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.M(m-1,y1),N(m+1,y2)为图形G上两点,若y1<y2,则m的取值范围是( )
A.m<-1或m>0 B. C.0≤m< D.-1
11.抛物线y=x2﹣2x+3的图象与y轴的交点坐标为 .
12.已知二次函数中,函数y与自变量x的部分对应值如下表:
x … -2 -1 0 1 2 …
y … -3 -4 -3 0 5 …
则此二次函数的对称轴为
13.点在第二象限内,点,则的取值范围是 .
14.已知二次函数 的图象与x轴没有公共点,且当 时,y随x的增大而减小,则实数a的取值范围是 .
15. 关于的二次函数,在时有最大值6,则 .
16.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(4,4),小车沿抛物线y=ax2﹣2ax﹣3a(a<0)运动.若小车在运动过程中只触发一次报警装置,则a的取值范围是 .
三、解答题
17.已知函数 (为常数).
(1)求当为何值时是的二次函数?
(2)在()的条件下,点在此函数图象上,求的值.
18.已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
19.杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体看成一点的路线是抛物线的一部分,如图所示.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
20. 如图,在平面直角坐标系中,直线分别交x轴,y轴于A,B两点.抛物线经过A,B两点,且与x轴的另一个交点为.
(1)求该抛物线的解析式.
(2)若点P是线段AB上一个动点,过点P作x轴的垂线,交该抛物线于点Q,连接AQ,BQ,求面积的最大值.
21.阅读理解:
某“数学兴趣小组”根据学习函数的经验,对函数的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
… …
… …
其中 ;
(2)在平面直角坐标系中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)根据函数图象,回答下列问题:
①当时,则y的取值范围为 .
②直线经过点,若关于x的方程有4个互不相等的实数根,则b的取值范围是 .
22.已知二次函数.
(1)当时,
①求该函数图象向顶点坐标.
②当时,求的取值范围.
(2)当时,的最大值为2;当时,的最大值为3,求二次函数的表达式.
23.问题提出:
四边形是正方形,是射线上的动点,点在线段的延长线上,且,连接,将线段绕点顺时针旋转得到,连接,设,四边形的面积为(可等于0).
(1)如图①,当点由点运动到点过程中,发现是关于的二次函数,并绘制成如图②所示的图象,抛物线经过原点且顶点为,请根据图象信息,回答下列问题:
①正方形的边长为___________(直接填空);
②求关于的函数关系式;
(2)如图③,当点在线段的延长线上运动时,求关于的函数关系式;
(3)若在射线上从下至上依次存在不同位置的两个点,对应的四边形的面积与四边形的面积相等,当时,求四边形的面积.
参考答案
1.C
2.C
3.A
4.B
5.B
6.C
7.A
8.D
解:如图所示:当直线y=﹣x+m与新图象有3个交点时,会有①②两种情况:
∵二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,
∴ 其与x轴的交点A(-2,0),下翻的图象解析式y=x2-x-6
当直线y=﹣x+m与新图象有3个交点时,此时直线过点A(-2,0)
∴ -(-2)+m=0
∴ m=-2
当直线y=﹣x+m与新图象有3个交点时,此时直线与下翻的图象解析式y=x2-x-6只有1个交点
∴ x2-x-6=-x+m
∴x2-6-m=0
∴=-4(-6-m)=0
解得m=-6
综上,当直线y=﹣x+m与新图象有3个交点时,m的值是-6或-2
9.B
解:∵与x轴的一个交点为,
∴存在实数根,
∴,
解得,
当k≤-5时,画出图像如图所示:
∴当x=-2时,,
解得,
当k≥1时,画出图像如图所示:
当x=-2时,,
解得,
∴,
10.D
解:在y=-x2+2mx-m2+2中,当x=m-1时,y=-(m-1)2+2m(m-1)-m2+2=1,
当x=m+1时,y=-(m+1)2+2m(m+1)-m2+2=1,
∴(m-1,1)和(m+1,1)是关于抛物线y=-x2+2mx-m2+2对称轴对称的两点,
若m-1≥0,即(m-1,1)和(m+1,1)在y轴右侧或(m-1,1)在y轴上,(m+1,1)在y轴右侧,
则点(m-1,1)经过翻折得M(m-1,y1),点(m+1,1)经过翻折得N(m+1,y2),
如图:
由对称性可知,y1=y2,
∴此时不满足y1<y2;
若m+1≤0,即(m-1,1)和(m+1,1)在y轴左侧或(m+1,1)在y轴上,(m-1,1)在y轴左侧,
则点(m-1,1)即为M(m-1,y1),点(m+1,1)即为N(m+1,y2),
∴y1=y2,
∴此时不满足y1<y2;
若m-1<0<m+1,即(m-1,1)在y轴左侧,(m+1,1)在y轴右侧时,如图:
此时M(m-1,1),(m+1,1)翻折后得N,满足y1<y2;
∵m-1<0<m+1,
解得:-1<m<1,
故答案为:D
11.(0,3)
12.x=-1
13.
14.-1≤a<2
解:由题意得:△ ,解得 ,
,故抛物线开口向上,对称轴为x=a
当 时, 随 的增大而减小,则 ,
实数 的取值范围是-1≤a<2.
15.2或
解:y=ax2+a2,
①当a>0时,二次函数的对称轴为x=0,
∴x=-1时,ymax=a+a2=6,
解得:a=2或a=-3(舍去);
②当a<0时,二次函数的对称轴为x=0,
∴x=0时,ymax=a2=6,
解得:a=或a=(舍去),
综上所述,a=2或.
16.a=﹣1或a<﹣ 或a>
解:抛物线y=ax2﹣2ax﹣3a=a(x+1)(x﹣3),
∴其对称轴为:x=1,且图象与x轴交于(﹣1,0),(3,0).
∵抛物线顶点为(1,﹣4a),当顶点在线段AB上时,﹣4a=4,则a=﹣1;
当抛物线过点(0,4)时,代入解析式得4=﹣3a,∴a=﹣ ,
由对称轴为x=1及图象与x轴交于(﹣1,0),(3,0)可知,当a<﹣ 时,抛物线与线段AB只有一个交点;
当抛物线过点(4,4)时,代入解析式得16a﹣8a﹣3a=4,
∴a= ,同理可知当a> 时,抛物线与线段AB只有一个交点.
17.(1);
(2)
18.(1)y=﹣x2﹣2x+3;(2)点P(﹣2,3)在这个二次函数的图象上,
19.(1)解:根据题意可知,抛物线方程为 ,可知二次项系数a=-,a<0,抛物线图像开口向下,所以存在最大值,
对抛物线方程为 ,进行化简得:
y=-+,
可知当x=时,抛物线对应的值最大,最大值为:
因此演员弹跳的最大高度是米.
(2)解:当x=4时,y=-×42+3×4+1=3.4=BC,
所以这次表演成功.
20.(1)抛物线解析式为:
(2)解:如图,设点P的横坐标为m,则,,
∴,
∵,
∴,
∵,
∴当时,面积的最大值为
21.(1)1
(2)解:根据表格:
… …
… …
描点法作出函数的图象如下图所示:
(3);
22.(1)解:①顶点坐标为(2,7).
②当-1≤x≤3时,-2≤y≤7.
(2)解:∵当x≤0时,y的最大值为2;当x>0时,y的最大值为3,
∴抛物线的对称轴在y轴的右侧,b>0.
∵抛物线开口向下,当x≤0时,y的最大值为2,∴c=2,
又∵当x>0时,y的最大值为3,∴,
∴b=±2.
∵b>0,
∴b=2.
∴二次函数的表达为y=-x2+2x+2.
23.(1)①4; ②
(2);
(3)四边形的面积为3或.
1 / 1
同课章节目录
