2024-2025学年广西南宁三十七中八年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广西南宁三十七中八年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 10:12:57 | ||
图片预览



文档简介
2024-2025学年广西南宁三十七中八年级(上)开学数学试卷
一、选择题:本题共13小题,共38分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,是无理数的是( )
A. B. C. D.
2.“水是生命之源,滋润着世间万物”国家节水标志由水滴,手掌和地球变形而成.寓意:像对待掌上明珠一样,珍惜每一滴水以下通过平移节水标志得到的图形是( )
A. B. C. D.
3.在平面直角坐标系中,点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.如图,直线,相交于点,,则的度数是( )
A. B.
C. D.
5.下列调查中,适合普查的是( )
A. 了解全国中学生的睡眠时间 B. 了解一批灯泡的使用寿命
C. 调查长江中下游的水质情况 D. 对乘坐飞机的乘客进行安检
6.下列各对数值中是方程的解的是( )
A. B. C. D.
7.下列四个选项中,与是同位角的是( )
A. B. C. D.
8.埃菲尔铁塔是巴黎城市地标之一,也是巴黎最高的建筑物,总高米,如图所示,在埃菲尔铁塔的设计中运用了大量的三角形的结构,你能从中推断出其运用的数学原理是( )
A. 三角形的不稳定性
B. 三角形的稳定性
C. 三角形两边之和大于第三边
D. 两点之间线段最短
9.已知,则下列结论正确的是( )
A. B. C. D.
10.将方程改写成用含的式子表示的形式,结果是( )
A. B. C. D.
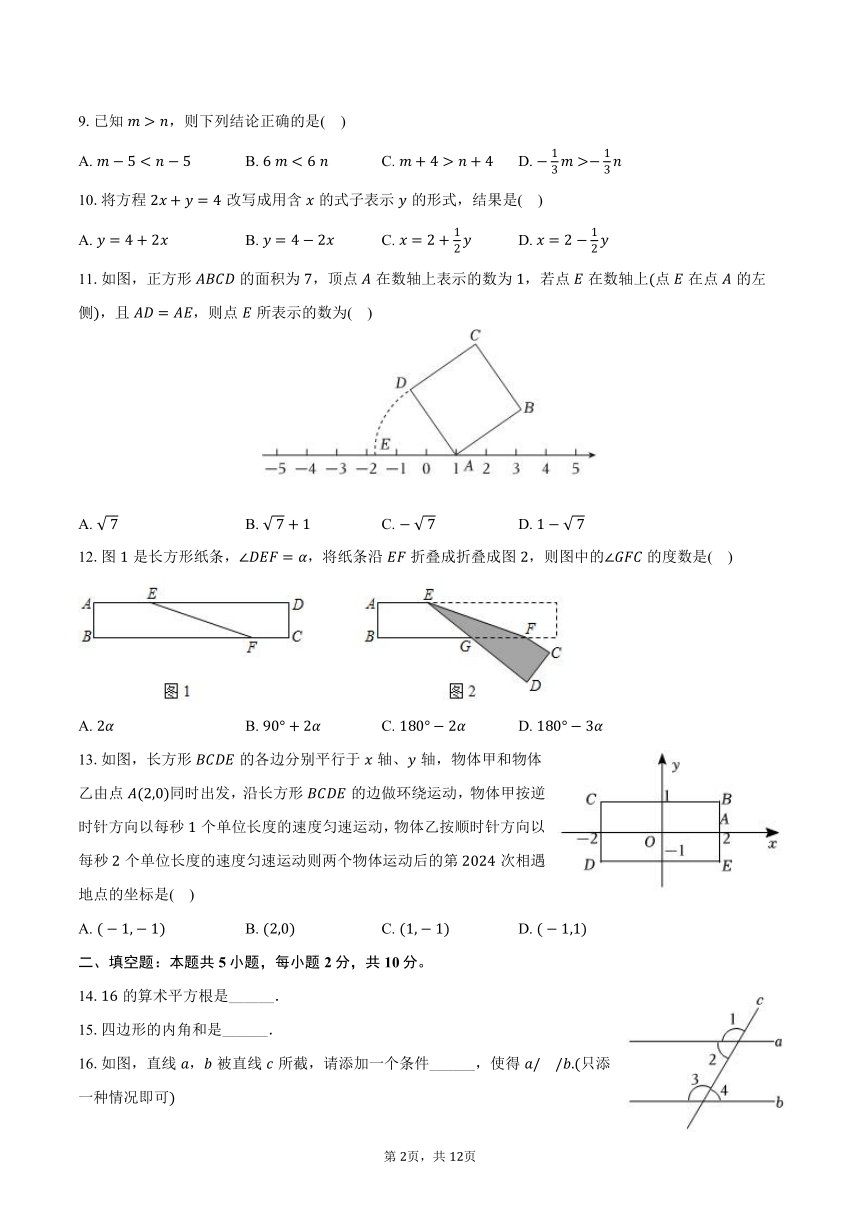
11.如图,正方形的面积为,顶点在数轴上表示的数为,若点在数轴上点在点的左侧,且,则点所表示的数为( )
A. B. C. D.
12.图是长方形纸条,,将纸条沿折叠成折叠成图,则图中的的度数是( )
A. B. C. D.
13.如图,长方形的各边分别平行于轴、轴,物体甲和物体乙由点同时出发,沿长方形的边做环绕运动,物体甲按逆时针方向以每秒个单位长度的速度匀速运动,物体乙按顺时针方向以每秒个单位长度的速度匀速运动则两个物体运动后的第次相遇地点的坐标是( )
A. B. C. D.
二、填空题:本题共5小题,每小题2分,共10分。
14.的算术平方根是______.
15.四边形的内角和是______.
16.如图,直线,被直线所截,请添加一个条件______,使得只添一种情况即可
17.如果在轴上,则的值为______.
18.已知,是二元一次方程组的解,那么的值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
解不等式组:,并利用数轴确定不等式组的解集.
21.本小题分
如图,在边长均为个单位长度的小正方形网格中,的顶点均在格点网格线的交点上,若记点的坐标为,点的坐标为.
请在图中画出平面直角坐标系;
把向上平移个单位长度,再向右平移个单位长度,得到,画出平移后的图形,并写出点的坐标;
求的面积.
22.本小题分
某校为了解本校名初中生对安全知识掌握情况,随机抽取了名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制了如下不完整的频数统计表和频数直方图:
组别 成绩分 频数人数
第组
第组
第组
第组
第组
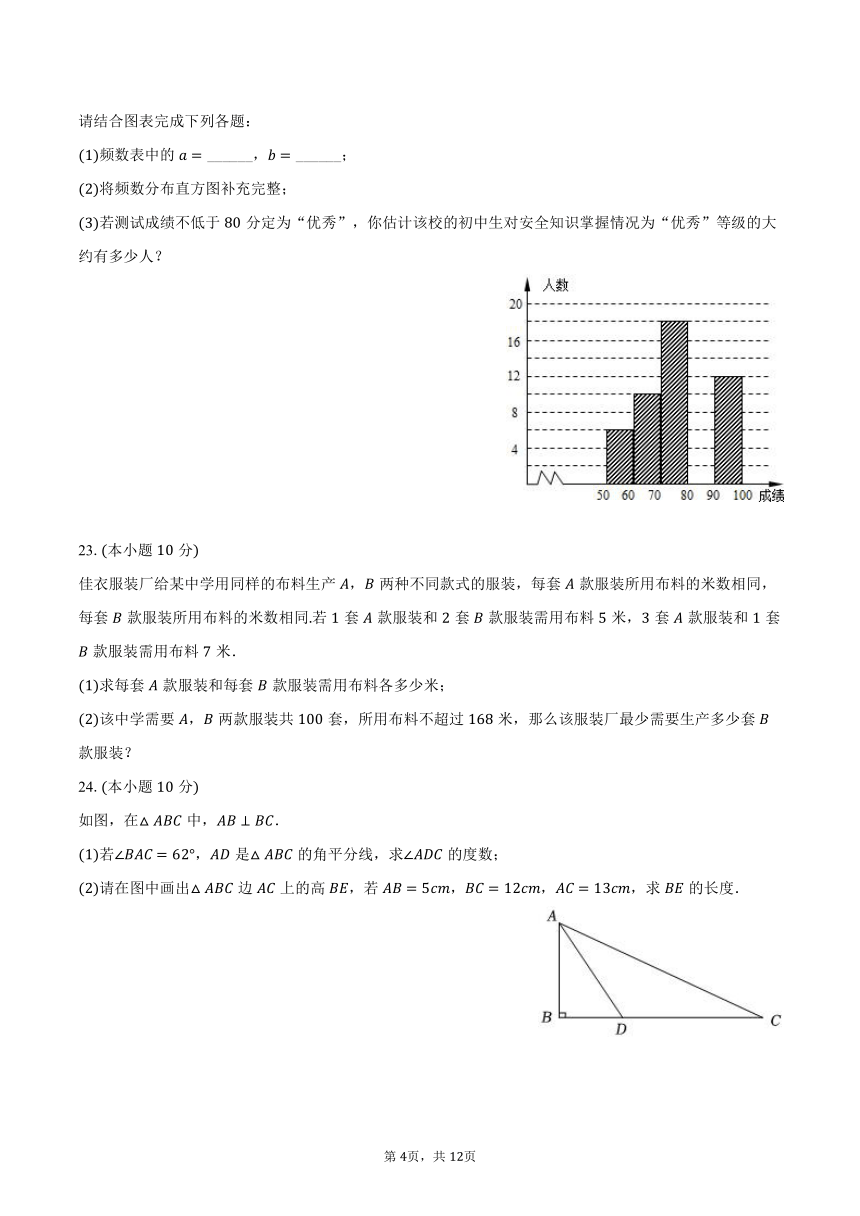
请结合图表完成下列各题:
频数表中的 ______, ______;
将频数分布直方图补充完整;
若测试成绩不低于分定为“优秀”,你估计该校的初中生对安全知识掌握情况为“优秀”等级的大约有多少人?
23.本小题分
佳衣服装厂给某中学用同样的布料生产,两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.
求每套款服装和每套款服装需用布料各多少米;
该中学需要,两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?
24.本小题分
如图,在中,.
若,是的角平分线,求的度数;
请在图中画出边上的高,若,,,求的长度.
25.本小题分
根据下列信息,探索完成任务:
信息一 年巴黎奥运会,即第届夏季奥林匹克运动会,是由法国巴黎举办的国际性奥林匹克赛事,年月日本届奥运会在巴黎塞纳河上举行开幕式某校七年级举行了关于“奥林匹克运动会”的线上知识竞赛,竞赛试卷共道题目,每道题都给出四个答案,其中只有一个答案正确,参赛者选对得分,不选或者选错扣分,得分不低于分者获奖.
信息二 为奖励获奖同学,学校准备购买、两种文具作为奖品,已知购买个型文具和个型文具共需元,购买个型文具和购买个型文具所花的钱一样多.
信息三 学校计划完成本次活动的总费用包含支付线上平台使用费和购买奖品两部分不超过元,其中支付线上平台使用费刚好用了元,剩余的钱用于购买两种型号的文具共个作为奖品,其中型文具数量大于个.
解决问题
任务一 小明同学是获奖者,他至少应选对多少道题.
任务二 求型文具和型文具的单价.
任务三 通过计算说明该校共有哪几种购买方案.
26.本小题分
如图,直线,被直线所截,,交于点.
若,则的度数为______
若,判断直线与的位置关系,并说明理由;
在的条件下,点在射线上运动,连接,的角平分线交于点,交于点,如图,当三角形的边与直线平行时,求出与的数量关系.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.答案不唯一
17.
18.
19.解:原式
.
20.解:,
解不等式得:,
解不等式得:,
不等式组的解集是.
在数轴上表示为:
21.解:画出平面直角坐标系如图所示;
如图所示,为所求;
则;
.
22.;
根据求出的的值,补图如下:
“优秀”等级的人数为:人.
答:估计该校的初中生对安全知识掌握情况为“优秀”等级的大约有人.
23.解:设每套款服装需用布料米,每套款服装需用布料米,
根据题意得:,
解得:.
答:每套款服装需用布料米,每套款服装需用布料米;
设该服装厂需要生产套款服装,则需要生产套款服装,
根据题意得:,
解得:,
的最小值为.
答:该服装厂最少需要生产套款服装.
24.解:,
,
,
,
是的角平分线,
,
;
高线如图:
,,
,
,,,
.
25.解:任务一:设小明同学选对道题,则不选或者选错的有道题,
根据题意,可得,
解得,
若小明同学是获奖者,他至少应选对道题;
任务二:设型文具的单价为元,型文具的单价为元,
根据题意,可得,
解得,
型文具的单价为元,型文具的单价为元;
任务三:设学校购买型文具个,则购买型文具个,
根据题意,可得,
解得,
为整数,
,,
购买方案有:
购买型文具个,购买型文具个;
购买型文具个,购买型文具个;
综上,该校共购买型文具个,购买型文具个;购买型文具个,购买型文具个两种购买方案.
26.;
证明:由知,
,
,
,
;
解:如图,当时,则,
,,
,,
是的角平分线,
,
,,
,即,
,
,
,
,
,即;
如图,当时,
,,
,,
,
,
,
,
,即;
综上,当三角形的边与直线平行时,或.
第1页,共1页
一、选择题:本题共13小题,共38分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,是无理数的是( )
A. B. C. D.
2.“水是生命之源,滋润着世间万物”国家节水标志由水滴,手掌和地球变形而成.寓意:像对待掌上明珠一样,珍惜每一滴水以下通过平移节水标志得到的图形是( )
A. B. C. D.
3.在平面直角坐标系中,点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.如图,直线,相交于点,,则的度数是( )
A. B.
C. D.
5.下列调查中,适合普查的是( )
A. 了解全国中学生的睡眠时间 B. 了解一批灯泡的使用寿命
C. 调查长江中下游的水质情况 D. 对乘坐飞机的乘客进行安检
6.下列各对数值中是方程的解的是( )
A. B. C. D.
7.下列四个选项中,与是同位角的是( )
A. B. C. D.
8.埃菲尔铁塔是巴黎城市地标之一,也是巴黎最高的建筑物,总高米,如图所示,在埃菲尔铁塔的设计中运用了大量的三角形的结构,你能从中推断出其运用的数学原理是( )
A. 三角形的不稳定性
B. 三角形的稳定性
C. 三角形两边之和大于第三边
D. 两点之间线段最短
9.已知,则下列结论正确的是( )
A. B. C. D.
10.将方程改写成用含的式子表示的形式,结果是( )
A. B. C. D.
11.如图,正方形的面积为,顶点在数轴上表示的数为,若点在数轴上点在点的左侧,且,则点所表示的数为( )
A. B. C. D.
12.图是长方形纸条,,将纸条沿折叠成折叠成图,则图中的的度数是( )
A. B. C. D.
13.如图,长方形的各边分别平行于轴、轴,物体甲和物体乙由点同时出发,沿长方形的边做环绕运动,物体甲按逆时针方向以每秒个单位长度的速度匀速运动,物体乙按顺时针方向以每秒个单位长度的速度匀速运动则两个物体运动后的第次相遇地点的坐标是( )
A. B. C. D.
二、填空题:本题共5小题,每小题2分,共10分。
14.的算术平方根是______.
15.四边形的内角和是______.
16.如图,直线,被直线所截,请添加一个条件______,使得只添一种情况即可
17.如果在轴上,则的值为______.
18.已知,是二元一次方程组的解,那么的值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
解不等式组:,并利用数轴确定不等式组的解集.
21.本小题分
如图,在边长均为个单位长度的小正方形网格中,的顶点均在格点网格线的交点上,若记点的坐标为,点的坐标为.
请在图中画出平面直角坐标系;
把向上平移个单位长度,再向右平移个单位长度,得到,画出平移后的图形,并写出点的坐标;
求的面积.
22.本小题分
某校为了解本校名初中生对安全知识掌握情况,随机抽取了名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制了如下不完整的频数统计表和频数直方图:
组别 成绩分 频数人数
第组
第组
第组
第组
第组
请结合图表完成下列各题:
频数表中的 ______, ______;
将频数分布直方图补充完整;
若测试成绩不低于分定为“优秀”,你估计该校的初中生对安全知识掌握情况为“优秀”等级的大约有多少人?
23.本小题分
佳衣服装厂给某中学用同样的布料生产,两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.
求每套款服装和每套款服装需用布料各多少米;
该中学需要,两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?
24.本小题分
如图,在中,.
若,是的角平分线,求的度数;
请在图中画出边上的高,若,,,求的长度.
25.本小题分
根据下列信息,探索完成任务:
信息一 年巴黎奥运会,即第届夏季奥林匹克运动会,是由法国巴黎举办的国际性奥林匹克赛事,年月日本届奥运会在巴黎塞纳河上举行开幕式某校七年级举行了关于“奥林匹克运动会”的线上知识竞赛,竞赛试卷共道题目,每道题都给出四个答案,其中只有一个答案正确,参赛者选对得分,不选或者选错扣分,得分不低于分者获奖.
信息二 为奖励获奖同学,学校准备购买、两种文具作为奖品,已知购买个型文具和个型文具共需元,购买个型文具和购买个型文具所花的钱一样多.
信息三 学校计划完成本次活动的总费用包含支付线上平台使用费和购买奖品两部分不超过元,其中支付线上平台使用费刚好用了元,剩余的钱用于购买两种型号的文具共个作为奖品,其中型文具数量大于个.
解决问题
任务一 小明同学是获奖者,他至少应选对多少道题.
任务二 求型文具和型文具的单价.
任务三 通过计算说明该校共有哪几种购买方案.
26.本小题分
如图,直线,被直线所截,,交于点.
若,则的度数为______
若,判断直线与的位置关系,并说明理由;
在的条件下,点在射线上运动,连接,的角平分线交于点,交于点,如图,当三角形的边与直线平行时,求出与的数量关系.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.答案不唯一
17.
18.
19.解:原式
.
20.解:,
解不等式得:,
解不等式得:,
不等式组的解集是.
在数轴上表示为:
21.解:画出平面直角坐标系如图所示;
如图所示,为所求;
则;
.
22.;
根据求出的的值,补图如下:
“优秀”等级的人数为:人.
答:估计该校的初中生对安全知识掌握情况为“优秀”等级的大约有人.
23.解:设每套款服装需用布料米,每套款服装需用布料米,
根据题意得:,
解得:.
答:每套款服装需用布料米,每套款服装需用布料米;
设该服装厂需要生产套款服装,则需要生产套款服装,
根据题意得:,
解得:,
的最小值为.
答:该服装厂最少需要生产套款服装.
24.解:,
,
,
,
是的角平分线,
,
;
高线如图:
,,
,
,,,
.
25.解:任务一:设小明同学选对道题,则不选或者选错的有道题,
根据题意,可得,
解得,
若小明同学是获奖者,他至少应选对道题;
任务二:设型文具的单价为元,型文具的单价为元,
根据题意,可得,
解得,
型文具的单价为元,型文具的单价为元;
任务三:设学校购买型文具个,则购买型文具个,
根据题意,可得,
解得,
为整数,
,,
购买方案有:
购买型文具个,购买型文具个;
购买型文具个,购买型文具个;
综上,该校共购买型文具个,购买型文具个;购买型文具个,购买型文具个两种购买方案.
26.;
证明:由知,
,
,
,
;
解:如图,当时,则,
,,
,,
是的角平分线,
,
,,
,即,
,
,
,
,
,即;
如图,当时,
,,
,,
,
,
,
,
,即;
综上,当三角形的边与直线平行时,或.
第1页,共1页
同课章节目录
