4.3.1等比数列的概念 教学设计(表格式)--2024--2025学年高中《数学》·选择性必修第二册人教A版
文档属性
| 名称 | 4.3.1等比数列的概念 教学设计(表格式)--2024--2025学年高中《数学》·选择性必修第二册人教A版 |  | |
| 格式 | docx | ||
| 文件大小 | 863.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-01 23:21:27 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 高二 学期 秋季
课题 等比数列的概念
教科书 书 名:数学选择性必修第二册教材 出版社:人民教育出版社 出版日期:2020年5月
教学目标
1. 能够运用等比数列的知识解决简单的实际问题. 2. 探究发现等差与等比数列的联系,并能解决相关问题.
教学内容
教学重点: 实际问题数学模型化的探究,等比数列与等差数列的联系.
教学难点: 实际问题数学化成等比数列问题的分析与理解
教学过程
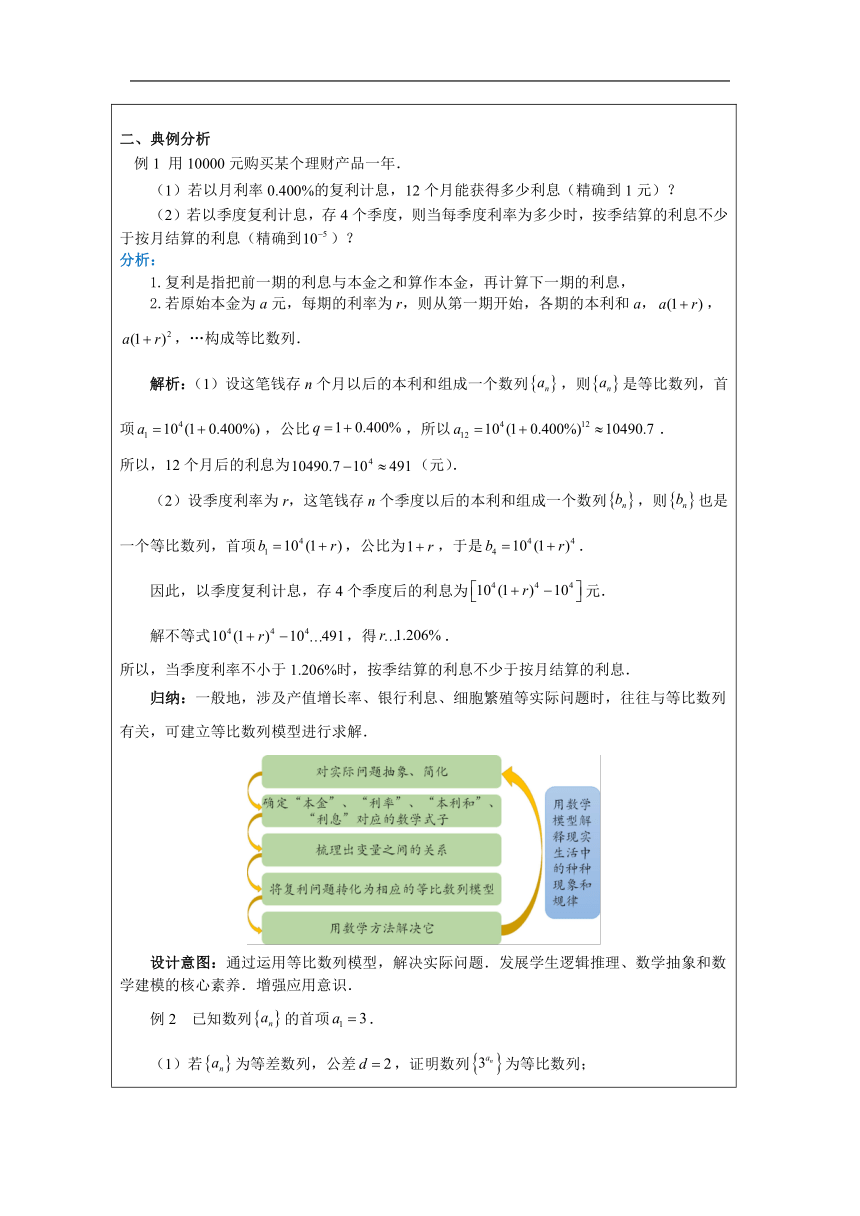
一、复习巩固 等比数列:如果一个数列从第 二 项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示(显然). 符号表示:. 通项公式: 函数性质: 等比数列:的单调性单调递减 单调递增 无单调性单调递增单调递减无单调性
二、典例分析 例1 用10000元购买某个理财产品一年. (1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)? (2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)? 分析: 1.复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息, 2.若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,,,…构成等比数列. 解析:(1)设这笔钱存n个月以后的本利和组成一个数列,则是等比数列,首项,公比,所以. 所以,12个月后的利息为(元). (2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列,则也是一个等比数列,首项,公比为,于是. 因此,以季度复利计息,存4个季度后的利息为元. 解不等式,得. 所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息. 归纳:一般地,涉及产值增长率、银行利息、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解. 设计意图:通过运用等比数列模型,解决实际问题.发展学生逻辑推理、数学抽象和数学建模的核心素养.增强应用意识. 例2 已知数列的首项. (1)若为等差数列,公差,证明数列为等比数列; (2)若为等比数列,公比,证明数列为等差数列. 分析:根据题意,需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明. 【证明】(1)由,,得的通项公式为. 设,则. 又,所以,是以27为首项,9为公比的等比数列. (2)由,,得.两边取以3为底的对数,得. 所以. 又,所以,是首项为1,公差为的等差数列. 结论:1.若是等差数列,则数列是等比数列; 2.若数列是各项均为正的等比数列,则数列是等差数列 设计意图:通过典型例题,加深对等差与等比数列概念的理解,体会等差与等比数列的内在联系。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素。 例3 设等比数列满足,,则的最大值为 . 解析一:等比数列满足,即,解得. 则, 当或4时,表达式取得最大值为.故答案为64. 解析二:等比数列满足,即,解得. 则,记, 则,两式相乘,得,所以. 后面解析同方法一. 设计意图:通过典型例题,加深学生对等比数列综合运用能力。发展学生逻辑推理和数学运算的核心素. 三、应用巩固 1.在9与243中间插入2个数,使这4个数成等比数列,则这两个数依次为 . 答案:27、81 解析:在9与243中间插入2个数,使这4个数成等比数列,设等比数列的公比为, 则,解得,所以在9与243中间插入2个数为、. 2.正项等比数列满足,则的最小值为( ) A. B. C. D. 答案:C 解析:设等比数列的公比为,由已知可得, 则有,所以 , 当且仅当即等号成立. 四、课堂小结 等差数列等比数列不同点(1)每一项与前一项的差; (2)和可以为零; (3)等差中项唯一.(1)每一项与前一项的比; (2)和均不为零; (3)等差中项有两个值.相同点(1)都强调每一项与前一项的关系; (2)差(比)都必须是常数; (3)数列都可以由或确定.联系(1)若为正项等比数列,则为等差数列; (2)若为等差数列,为等比数列,则为等比数列.
★掌握建模法求解等比数列有关的实际问题. 五、布置作业 完成作业练习
课程基本信息
学科 数学 年级 高二 学期 秋季
课题 等比数列的概念
教科书 书 名:数学选择性必修第二册教材 出版社:人民教育出版社 出版日期:2020年5月
教学目标
1. 能够运用等比数列的知识解决简单的实际问题. 2. 探究发现等差与等比数列的联系,并能解决相关问题.
教学内容
教学重点: 实际问题数学模型化的探究,等比数列与等差数列的联系.
教学难点: 实际问题数学化成等比数列问题的分析与理解
教学过程
一、复习巩固 等比数列:如果一个数列从第 二 项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示(显然). 符号表示:. 通项公式: 函数性质: 等比数列:的单调性单调递减 单调递增 无单调性单调递增单调递减无单调性
二、典例分析 例1 用10000元购买某个理财产品一年. (1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)? (2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)? 分析: 1.复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息, 2.若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,,,…构成等比数列. 解析:(1)设这笔钱存n个月以后的本利和组成一个数列,则是等比数列,首项,公比,所以. 所以,12个月后的利息为(元). (2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列,则也是一个等比数列,首项,公比为,于是. 因此,以季度复利计息,存4个季度后的利息为元. 解不等式,得. 所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息. 归纳:一般地,涉及产值增长率、银行利息、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解. 设计意图:通过运用等比数列模型,解决实际问题.发展学生逻辑推理、数学抽象和数学建模的核心素养.增强应用意识. 例2 已知数列的首项. (1)若为等差数列,公差,证明数列为等比数列; (2)若为等比数列,公比,证明数列为等差数列. 分析:根据题意,需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明. 【证明】(1)由,,得的通项公式为. 设,则. 又,所以,是以27为首项,9为公比的等比数列. (2)由,,得.两边取以3为底的对数,得. 所以. 又,所以,是首项为1,公差为的等差数列. 结论:1.若是等差数列,则数列是等比数列; 2.若数列是各项均为正的等比数列,则数列是等差数列 设计意图:通过典型例题,加深对等差与等比数列概念的理解,体会等差与等比数列的内在联系。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素。 例3 设等比数列满足,,则的最大值为 . 解析一:等比数列满足,即,解得. 则, 当或4时,表达式取得最大值为.故答案为64. 解析二:等比数列满足,即,解得. 则,记, 则,两式相乘,得,所以. 后面解析同方法一. 设计意图:通过典型例题,加深学生对等比数列综合运用能力。发展学生逻辑推理和数学运算的核心素. 三、应用巩固 1.在9与243中间插入2个数,使这4个数成等比数列,则这两个数依次为 . 答案:27、81 解析:在9与243中间插入2个数,使这4个数成等比数列,设等比数列的公比为, 则,解得,所以在9与243中间插入2个数为、. 2.正项等比数列满足,则的最小值为( ) A. B. C. D. 答案:C 解析:设等比数列的公比为,由已知可得, 则有,所以 , 当且仅当即等号成立. 四、课堂小结 等差数列等比数列不同点(1)每一项与前一项的差; (2)和可以为零; (3)等差中项唯一.(1)每一项与前一项的比; (2)和均不为零; (3)等差中项有两个值.相同点(1)都强调每一项与前一项的关系; (2)差(比)都必须是常数; (3)数列都可以由或确定.联系(1)若为正项等比数列,则为等差数列; (2)若为等差数列,为等比数列,则为等比数列.
★掌握建模法求解等比数列有关的实际问题. 五、布置作业 完成作业练习
