第五章 一元函数的导数及其应用 小结 课件(共25张PPT)--2024--2025学年高中《数学》·选择性必修第二册人教A版
文档属性
| 名称 | 第五章 一元函数的导数及其应用 小结 课件(共25张PPT)--2024--2025学年高中《数学》·选择性必修第二册人教A版 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 09:42:13 | ||
图片预览








文档简介
(共25张PPT)
导数小结
主讲教师:李青青
学 校:瑞安市塘下中学
年 级:高二
学 科:高中数学(人教A版)
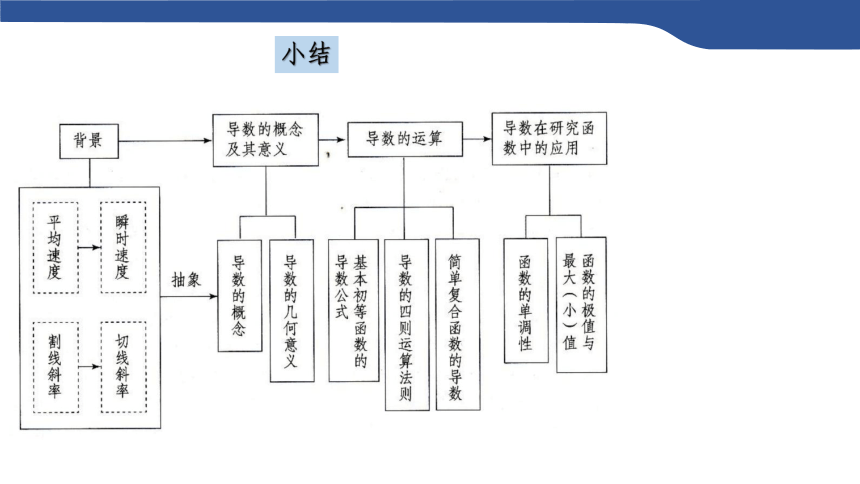
小结
高中数学选择性必修第二册——第五章 一元函数的导数及其应用
复习引入:阅读教材P102-P103,并思考以下问题。
1.平均变化率与瞬时变化率之间有什么内在联系?
2.你能从物理和几何两方面解释导数的意义吗?
3.利用导数定义推导函数的导数时,其基本步骤是什么?
4.导数的四则运算法则是什么?如何求简单复合函数的导数?
5.利用导数研究函数性质的基本步骤是什么?
6.通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
问题1:平均变化率与瞬时变化率之间有什么内在联系?
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念. 我们把物体在某一时刻的速度称为瞬时速度(instantaneous velocity).
平均速度:
瞬时速度:
问题2:你能从物理和几何两方面解释导数的意义吗?
物理问题:
跳水运动员起跳后的速度问题
几何问题:
抛物线的切线斜率问题
切线斜率
割线斜率
瞬时速度
平均速度
瞬时变化率
平均变化率
取极限
取极限
取极限
逼近
B
A
切线斜率
割线斜率
以直代曲
问题3:利用导数定义推导函数的导数时,其基本步骤是什么?
以“求函数的导数”为例
(1)求函数的变化量:
(2)求平均变化率:
当x=x0时,可求得
(3)若 极限存在,
取极限,得导数:
0
教材:P74
问题4:导数的四则运算法则是什么?
探究:设f(x)=x2,g(x)=x,计算[f(x)+g(x)]′与[f(x)-g(x)]′,它们与f'(x)和g'(x)有什么关系 再取几组函数试试,上述关系仍然成立吗 由此你能想到什么
导数的四则运算法则
(2)[f(x)·g(x)]′=f'(x)g(x)+f(x)g'(x)
(1)[f(x)±g(x)]′=f'(x)±g'(x)
特别地,有[cf(x)]′=cf ′(x)
问题5:如何求简单复合函数的导数?
复合函数 y = f( g(x) ) 的导数和函数 y = f(u), u = g(x) 的导数间的关系为
yx = yu ·ux ,
即 y 对 x 的导数等于 y 对 u 的导数与 u 对 x 的导数的乘积.
典例示范:
导数小结(第二课时)
主讲教师:李青青
学 校:瑞安市塘下中学
年 级:高二
学 科:高中数学(人教A版)
高中数学选择性必修第二册——第五章 一元函数的导数及其应用
复习引入:阅读教材P102-P103,并思考以下问题。
1.平均变化率与瞬时变化率之间有什么内在联系?
2.你能从物理和几何两方面解释导数的意义吗?
3.利用导数定义推导函数的导数时,其基本步骤是什么?
4.导数的四则运算法则是什么?如何求简单复合函数的导数?
5.利用导数研究函数性质的基本步骤是什么?
6.通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
小结
问题1:导数与函数单调性的关系?
设函数在区间(a , b)内可导, 则
① 如果 , 那么在内为增函数.
② 如果, 那么 在内为减函数.
③ 如果, 那么在内为常数函数.
但是,
如果 在内(或)
个点 ),
那么在内仍为增函数(或减函数).
(其中有限
如 在上是增函数,而它在 处的导数等于0.
函数的极大、极小值
问题2:函数极值与函数最值的关系?
在闭区间上连续的函数必有最大值和最小值.
①求函数在内的极值;
求在上的最大值与最小值的步骤:
②求函数在区间端点的值;
③将函数在各极值与比较,其中最大的一个是最大值,最小的一个是最小值.
如果函数 在上连续,在内可导,那 么如何求 在内的最大值与最小值呢?
问题3:利用导数研究函数性质的基本步骤是什么?
以“”为例:
(1)确定函数的定义域;
(2)求出导数的零点(即 时,的值);
(3)用的零点将的定义域划分为若干个区间,列表给出 在各区间上的正负,由此得出函数在定义域内的单调性.
(4)确定极值点(极值);
导数应用之一——求单调性、极值、最值问题
求 的单调性、极值点及在[0,3]上的最值
导数应用之二——求切线问题
已知曲线,求在点处的切线方程
解:
又∵
∴
∴该点处切线为
变式:已知曲线,求过处的切线方程
导数应用之三——利用导数画图象
练习:教材P104T17:经典问题之 ----
组合函数的大致图象
定义域优先意识
注意:(1)不连续;(2)特殊点;(3)极限位置
问题4:通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
导数小结
主讲教师:李青青
学 校:瑞安市塘下中学
年 级:高二
学 科:高中数学(人教A版)
小结
高中数学选择性必修第二册——第五章 一元函数的导数及其应用
复习引入:阅读教材P102-P103,并思考以下问题。
1.平均变化率与瞬时变化率之间有什么内在联系?
2.你能从物理和几何两方面解释导数的意义吗?
3.利用导数定义推导函数的导数时,其基本步骤是什么?
4.导数的四则运算法则是什么?如何求简单复合函数的导数?
5.利用导数研究函数性质的基本步骤是什么?
6.通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
问题1:平均变化率与瞬时变化率之间有什么内在联系?
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念. 我们把物体在某一时刻的速度称为瞬时速度(instantaneous velocity).
平均速度:
瞬时速度:
问题2:你能从物理和几何两方面解释导数的意义吗?
物理问题:
跳水运动员起跳后的速度问题
几何问题:
抛物线的切线斜率问题
切线斜率
割线斜率
瞬时速度
平均速度
瞬时变化率
平均变化率
取极限
取极限
取极限
逼近
B
A
切线斜率
割线斜率
以直代曲
问题3:利用导数定义推导函数的导数时,其基本步骤是什么?
以“求函数的导数”为例
(1)求函数的变化量:
(2)求平均变化率:
当x=x0时,可求得
(3)若 极限存在,
取极限,得导数:
0
教材:P74
问题4:导数的四则运算法则是什么?
探究:设f(x)=x2,g(x)=x,计算[f(x)+g(x)]′与[f(x)-g(x)]′,它们与f'(x)和g'(x)有什么关系 再取几组函数试试,上述关系仍然成立吗 由此你能想到什么
导数的四则运算法则
(2)[f(x)·g(x)]′=f'(x)g(x)+f(x)g'(x)
(1)[f(x)±g(x)]′=f'(x)±g'(x)
特别地,有[cf(x)]′=cf ′(x)
问题5:如何求简单复合函数的导数?
复合函数 y = f( g(x) ) 的导数和函数 y = f(u), u = g(x) 的导数间的关系为
yx = yu ·ux ,
即 y 对 x 的导数等于 y 对 u 的导数与 u 对 x 的导数的乘积.
典例示范:
导数小结(第二课时)
主讲教师:李青青
学 校:瑞安市塘下中学
年 级:高二
学 科:高中数学(人教A版)
高中数学选择性必修第二册——第五章 一元函数的导数及其应用
复习引入:阅读教材P102-P103,并思考以下问题。
1.平均变化率与瞬时变化率之间有什么内在联系?
2.你能从物理和几何两方面解释导数的意义吗?
3.利用导数定义推导函数的导数时,其基本步骤是什么?
4.导数的四则运算法则是什么?如何求简单复合函数的导数?
5.利用导数研究函数性质的基本步骤是什么?
6.通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
小结
问题1:导数与函数单调性的关系?
设函数在区间(a , b)内可导, 则
① 如果 , 那么在内为增函数.
② 如果, 那么 在内为减函数.
③ 如果, 那么在内为常数函数.
但是,
如果 在内(或)
个点 ),
那么在内仍为增函数(或减函数).
(其中有限
如 在上是增函数,而它在 处的导数等于0.
函数的极大、极小值
问题2:函数极值与函数最值的关系?
在闭区间上连续的函数必有最大值和最小值.
①求函数在内的极值;
求在上的最大值与最小值的步骤:
②求函数在区间端点的值;
③将函数在各极值与比较,其中最大的一个是最大值,最小的一个是最小值.
如果函数 在上连续,在内可导,那 么如何求 在内的最大值与最小值呢?
问题3:利用导数研究函数性质的基本步骤是什么?
以“”为例:
(1)确定函数的定义域;
(2)求出导数的零点(即 时,的值);
(3)用的零点将的定义域划分为若干个区间,列表给出 在各区间上的正负,由此得出函数在定义域内的单调性.
(4)确定极值点(极值);
导数应用之一——求单调性、极值、最值问题
求 的单调性、极值点及在[0,3]上的最值
导数应用之二——求切线问题
已知曲线,求在点处的切线方程
解:
又∵
∴
∴该点处切线为
变式:已知曲线,求过处的切线方程
导数应用之三——利用导数画图象
练习:教材P104T17:经典问题之 ----
组合函数的大致图象
定义域优先意识
注意:(1)不连续;(2)特殊点;(3)极限位置
问题4:通过本章的学习,你对“导数是研究函数性质的基本工具”有什么体会?
