沪教版2024~2025学年七年级上学期数学第一次月考卷(含答案)
文档属性
| 名称 | 沪教版2024~2025学年七年级上学期数学第一次月考卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 763.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 00:00:00 | ||
图片预览




文档简介
沪2024~2025学年七年级上学期数学第一次月考卷(含答案)
一、单选题(每题3分,共18分)
1.单项式的系数和次数分别是( )
A.0,3 B.1,2 C.,3 D.3,
2.下列运算正确的是( )
A. B. C. D.
3.为了求的值,可令,则,因此,所以.请仿照以上推理计算出的值是( )
A. B. C. D.
4.下列运算错误的是( )
A. B.
C. D.
5.如图,如图,把四张大小相同的长方形卡片(如图1)按图2、图3两种方式放在一个底面为长方形(长比宽多2cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图2中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1比C2大( )
A.3cm B.4cm C.5cm D.6cm
6.有个依次排列的整式,第一个整式为,第二个整式为,第二个整式减去第一个整式的差记为,将记为,将第二个整式加上作为第三个整式,将记为,将第三个整式与相加记为第四个整式,以此类推.以下结论正确的个数是( )
①;②当时,第四个整式的值为81;③若第三个整式与第四个整式的和为25,则;④第2023个整式为.
A.1 B.2 C.3 D.4
二、填空题
7.若多项式的结果是一个多项式的平方,则单项式 .(只填一个你认为正确的答案)
8.分解因式: .
9.因式分解:ax2﹣8ax+16a= .
10.如图,搭一个三角形需要根火柴,搭两个三角形需要根火柴,搭三个三角形需要根火柴,,按这个规律,搭个这样的三角形的需要火柴棒根数为 .
11.的个位数字是 .
12.观察下列等式:,,,,,,,,根据上述规律可得的结果的个位数字是 .
13.观察下列算式,你发现了什么规律?
(1)根据你发现的规律,计算下面算式的值:
(2)请用一个含n的算式表示这个规律: ;
14.若的积中,“”项的系数为,则 .
15.已知:a,b,c都是正整数,且,.abc的最大值为M,最小值为N,则 .
16.单项式的系数与次数的和是 .
17.计算: .
18.把多项式分解因式时,应提取的公因式是 .
三、解答题
19.计算:. 20.化简:
21.计算:.
22.先化简,再求值
(1)已知,求代数式的值.
(2)已知为正整数,且,求的值.
(3)若、满足,,求下列各式的值.
①;
②.
23.已知一个长方形的面积是,它的一边长为,用含a、b的式子表示长方形的另一边长.(需化简)
24.某农户去年承包荒山若干亩,投资17800元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元.该农户将水果拉到市场出售平均每天出售2000千克,需8人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天400元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若,元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到25000元,那么纯收入增长率是多少?(纯收入=总收入-总支出,该农户采用了(2)中较好的出售方式出售)
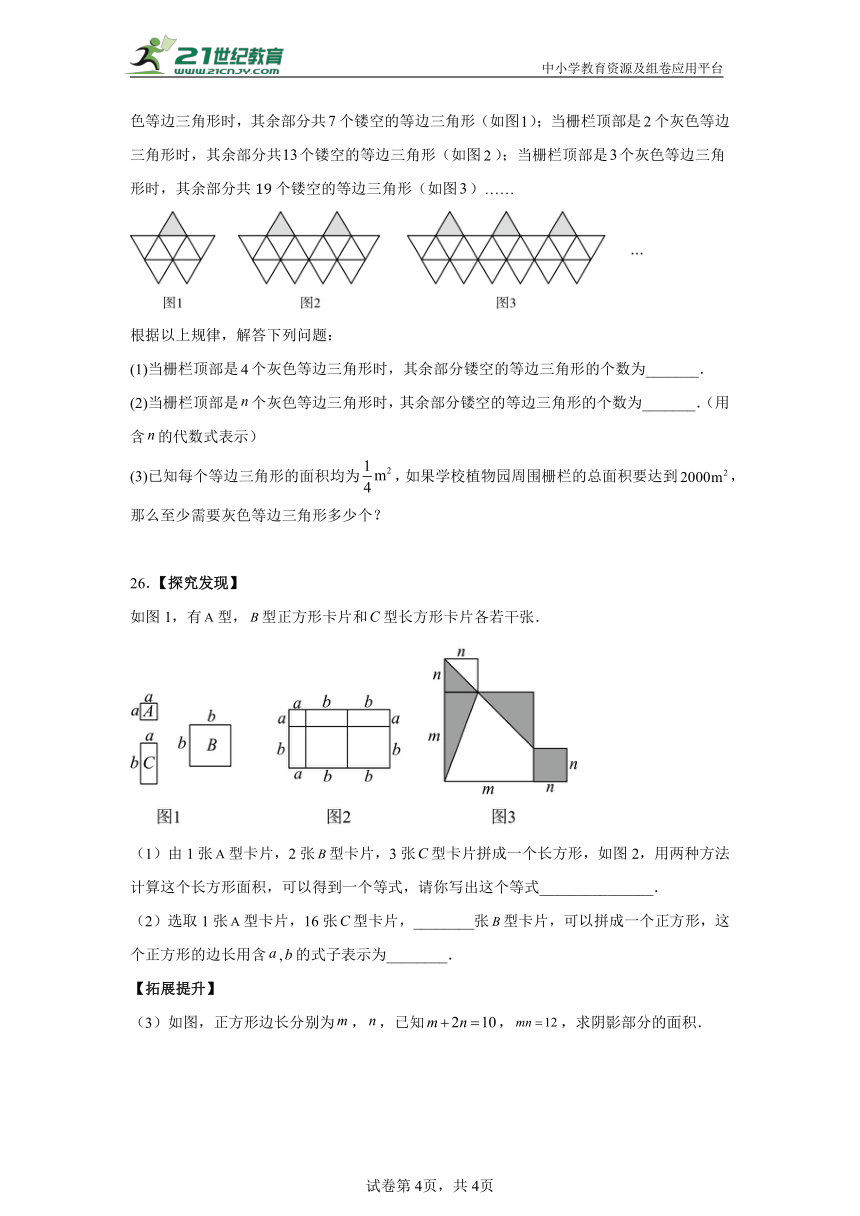
25.学校准备在植物园周围增设由大小相同的等边三角形组成的栅栏,当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图);当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图);当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图)……
根据以上规律,解答下列问题:
(1)当栅栏顶部是个灰色等边三角形时,其余部分镂空的等边三角形的个数为_______.
(2)当栅栏顶部是个灰色等边三角形时,其余部分镂空的等边三角形的个数为_______.(用含的代数式表示)
(3)已知每个等边三角形的面积均为,如果学校植物园周围栅栏的总面积要达到,那么至少需要灰色等边三角形多少个?
26.【探究发现】
如图1,有型,型正方形卡片和型长方形卡片各若干张.
(1)由1张型卡片,2张型卡片,3张型卡片拼成一个长方形,如图2,用两种方法计算这个长方形面积,可以得到一个等式,请你写出这个等式_______________.
(2)选取1张型卡片,16张型卡片,________张型卡片,可以拼成一个正方形,这个正方形的边长用含,的式子表示为________.
【拓展提升】
(3)如图,正方形边长分别为,,已知,,求阴影部分的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6
答案 C D D B B C
1.C
【分析】本题考查了单项式的次数和系数:单项式的数字因数是单项式的系数、字母的指数之和为单项式的次数,据此即可作答.
【详解】解:单项式的系数和次数分别是,3
故选:C.
2.D
【分析】根据同底数幂的运算法则,合并同类项,完全平方公式,逐个进行判断即可.
【详解】解:A、,故A不正确,不符合题意;
B、,故B不正确,不符合题意;
C、,故C不正确,不符合题意;
D、,故D正确,符合题意;
故选:D.
【点睛】本题主要考查了同底数幂的运算法则,合并同类项以及完全平方公式,解题的关键是掌握同底数幂相乘(除),底数不变,指数相加(减);幂的乘方,底数不变,指数相乘;积的乘方,把每个因式分别乘方;合并同类项,字母和相同字母是指数不变,只把系数相加减.
3.D
【分析】本题主要考查有理数的混合运算,考查了学生的分析、总结、归纳能力,规律题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结一般性的规律.
【详解】解:令,
则,
∴,
∴,
即,
故选:D.
4.B
【分析】本题主要考查了幂的运算,合并同类项等.熟练掌握同底数幂乘法的法则,积的乘方法则,商的乘方法则,幂的乘方法则,合并同类项法则,根据同底数幂乘法的法则,积的乘方法则,商的乘方法则,幂的乘方法则,合并同类项法则,逐一判断.
【详解】解:A.,
∵,A正确,不符合题意;
B.,
∵,B错误,符合题意;
C.,
∵,C正确,不符合题意;
D.,
∵,D正确,不符合题意.
故选:B.
5.B
【分析】设小长方形的长为a cm,宽为b cm,底面大长方形的宽为xcm,长为(x+)cm,再结合图形分别得出图形②的阴影周长和图形③的阴影周长,比较后即可求出答案.
【详解】解:设小长方形的长为a cm,宽为b cm,大长方形的宽为xcm,长为(x+2)cm,
∴②阴影周长为:2(x+2+x)=4x+4,
∴③左下阴影部分的周长为:2(x-2b+x+2-2b),右上阴影部分的周长为:2(x+2-a+x-a),
∴总周长为:2(x-2b+x+2-2b)+2(x+2-a+x-a)=4(x+2)+4x-4(a+2b),
又∵a+2b=x+2,
∴4(x+2)+4x-4(a+2b)=4x,
∴C2-C3=4x+4-4x=4(cm).
故选:B
【点睛】此题主要考查整式的加减的运用,做此类题要善于观察,在第②个图形中利用割补法进行计算,很容易计算得出结果.
6.C
【分析】先求出前几项的值,再求出,,的值,找到它们的变化规律,再逐一判断求解
【详解】解:由题意得:第一个整式为:,第二个整式为:,
∴,
,
;故①正确;
∴第三个整式为
第四个整式为
∴当时,第四个整式的值为,故②正确;
第2023个整式为,故④正确;
若第三个整式与第四个整式的和为25,则,解得,故③错误;
综上分析可知,正确的有3个.
故选:C.
【点睛】本题考查了数字的变化类,找到数字的变化规律是解题的关键.
7.或(任填一个即可)
【分析】分当M为中间项时,当为中间项时,两种情况根据完全平方式的特点进行求解即可.
【详解】解:当M为中间项时,则,
∴;
当为中间项时,则,
∴;
综上所述,或,
故答案为:或(任填一个即可).
【点睛】本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.
8./
【分析】本题考查因式分解,先提公因式,再利用完全平方公式分解因式,即可解题.
【详解】解:,
故答案为:.
9.
【分析】先提内参因式a,再运用公式法分解即可.
【详解】解:ax2-8ax+16a=a(x2-8x+16)=a(x-4)2,
故答案为:a(x-4)2.
【点睛】本题考查提公因式法和运用公式法分解因式.先提公因式,再用公式分解是解题的关键.注意:因式分解要分解到不能再分解为止.
10./
【分析】根据图形得出每增加一个三角形就增加了根火柴棒,据此得出答案.
【详解】解:搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
故答案为:.
【点睛】本题主要考查图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
11.5
【分析】将原式乘以凑出平方差公式的形式,按照平方差公式进行计算即可得出答案.
【详解】解:
,
∵,,,,,
∴指数4个数一个循环,
∵
∴尾数为6,
∴个位数字是5.
故答案为:5.
【点睛】本题考查的是平方差公式,能够将原式乘以凑出平方差公式的形式是解题的关键.
12.
【分析】观察所给等式发现规律末位数字为:,,,,,,,,每4个数一组循环,进而可得算式:结果的个位数字.
【详解】解:观察下列等式:,,,,,,,,
发现规律:末位数字为:,,,,,,,,
每4个数一组循环,
所以,而,
所有个位数字之和是.
所以算式:的结果的个位数字是.
故答案为:.
【点睛】本题考查了规律型—数字的变化类,解决本题的关键是根据数字的变化寻找规律.
13.
【分析】本题考查了含有乘方的有理数的混合运算,整式的混合运算,根据材料提示,找出计算规律即可求解,
(1)根据材料提示,找出规律计算即可;
(2)由材料、(1)中的规律,整式的混合运算进行计算即可求解.
【详解】解:(1)根据材料提示可得,;
(2)根据材料提示可得,
故答案为: ①;②.
14.4
【分析】先计算多项式乘以多项式,然后根据的系数为5求解即可.
【详解】解:
,
∵的系数为5,
∴ ,
解得,
故答案为:4.
【点睛】本题主要考查了多项式乘以多项式,解题的关键在于能够熟练掌握相关多项式乘以多项式进行求解.
15.
【分析】由已知条件整理出,再利用因式分解法转化为求的正整数解,据此得到或或或,据此解得a的值,最后代入计算即可.
【详解】解:,
,
,
,
,
,
,
,,都是正整数,
或或或,
或或或,
或,
即的最大值为,最小值为,即,,
∴,
故答案为:.
【点睛】本题考查因式分解法、二元一次方程组的整数解等知识,是重要考点,掌握相关知识是解题关键.
16.1
【分析】本题考查的是单项式的系数和次数,根据单项式的系数和次数的概念分别求出单项式的系数和次数,根据有理数的加法法则计算即可.
【详解】解:单项式的系数是,次数是2,
则单项式的系数与次数和为:,
故答案为:1.
17.
【分析】先计算单项式乘多项式,然后在合并同类项即可.
【详解】解:原式
故答案为:.
【点睛】本题是对整式乘法的考查,熟练掌握整式乘法运算是解决本题的关键.
18.
【分析】公因式的确定,一看系数:若各项系数都是整数,应提取各项系数的最大公因数;二看字母:公因式的字母是各项相同的字母;三看字母的指数:各相同字母的指数取指数最低的.
【详解】解:的公因式为.
故答案为:.
【点睛】本题考查了公因式的定义,熟练掌握公因式的定义是解答本题的关键.一个多项式的各项都含有的相同的因式叫做这个多项式各项的公因式.
19.(1);(2)
【分析】(1)根据多项式除以单项式的运算法则计算即可;
(2)根据平方差公式,多项式乘以单项式计算即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查多项式除以单项式,平方差公式,多项式乘以单项式,正确计算是解题的关键.
20.
【分析】利用合并同类项化简即可.
【详解】解:原式=
=
【点睛】本题考查了整式的合并同类项,注意不是同类项不能合并.
21.(1)
(2)
(3)
【分析】(1)运用乘法运算律求解即可;
(2)先计算乘方运算及小括号中的运算,然后计算乘除运算,最后计算加减运算即可;
(2)直接合并同类项计算即可.
【详解】(1)解:
;
(2)
;
(3)
.
【点睛】题目主要考查有理数的混合运算及整式的加减运算,熟练掌握运算法则是解题关键.
22.(1)-1;
(2)32;
(3)①;②.
【分析】(1)根据完全平方公式化简后,再把代入计算即可;
(2)根据幂的乘方的运算法则化简后,把代入计算即可;
(3)根据完全平方公式求解即可.
【详解】(1),
;
(2),
;
(3)①,,
;
(3),,
.
【点睛】本题主要考查了整式的混合运算,幂的乘方以及完全平方公式,熟记相关公式与运算法则是解答本题的关键.
23.
【分析】本题考查多项式除以单项式.利用长方形的面积除以边长进行求解即可.
【详解】解:由题意,得:长方形的另一边长为.
24.(1)拉到市场出售的收入为元;在果园出售的收入为元
(2)选择在果园直接出售比较好
(3)增长率为
【分析】(1)市场出售收入水果的总收入额外支出,而水果直接在果园的出售收入为:元.
(2)根据(1)中得到的代数式,将,,代入代数式计算即可.
(3)根据(2)的数据,首先确定今年的最高收入,然后计算增长率即可.
【详解】(1)解:将这批水果拉到市场上出售收入为:
(元),
故在果园直接出售收入为:元;
(2)解:当时,市场收入为(元.
当时,果园收入为(元,
因,所以应选择在果园直接出售;
(3)解:因为今年的纯收入为(元),,
所以增长率为.
【点睛】本题考查了根据实际问题列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解题的关键是读懂题意,正确表达.
25.(1)
(2)
(3)至少需要灰色等边三角形个
【分析】本题考查了图形规律及一元一次方程的应用,以镂空的等边三角形和灰色镂空的等边三角形的拼图为背景,关键是掌握规律性问题的解决方法,探究规律要认真观察、仔细思考,善用联想来解决这类问题.
()观察第个图案可知:中间的一个灰色镂空的等边三角形对应个镂空的等边三角形,第个图案可知增加一个灰色镂空的等边三角形,变成了个镂空的等边三角形,增加了个镂空的等边三角形,从而据此规律即可得解;
()观察第个图案,有个镂空的等边三角形;第个图案,有个镂空的等边三角形;,依次计算可解答;
()由()中的规律可知:,解方程即可解答.
【详解】(1)解:当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
故答案为:;
(2)解:第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
……
第个图案:镂空的等边三角形有:个,
故答案为:;
(3)解:,
,
按此规律镶嵌图案,需要灰色镂空的等边三角形个.
26.(1);(2)64;;(3)20
【分析】本题主要考查考查完全平方公式的几何意义,以及多项式乘以多项式玘几何图形的关系:
(1)用两种方法表示图2的面积,即可得出等式;
(2)由拼图可得是完全平方式,则,即,从而得出答案;
(3)表示阴影部分的面积,化成,再整体代入求值即可.
【详解】解:方法1:大长方形的面积为,
方法2:图2中五部分的面积和为:,
因此有;
故答案为:;
(2)由面积拼图可知,
故答案为:64,;
(3)由图形面积之间的关系可得,
.
∵,,
∴原式
故答案为:20
答案第1页,共2页
答案第1页,共2页
一、单选题(每题3分,共18分)
1.单项式的系数和次数分别是( )
A.0,3 B.1,2 C.,3 D.3,
2.下列运算正确的是( )
A. B. C. D.
3.为了求的值,可令,则,因此,所以.请仿照以上推理计算出的值是( )
A. B. C. D.
4.下列运算错误的是( )
A. B.
C. D.
5.如图,如图,把四张大小相同的长方形卡片(如图1)按图2、图3两种方式放在一个底面为长方形(长比宽多2cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图2中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1比C2大( )
A.3cm B.4cm C.5cm D.6cm
6.有个依次排列的整式,第一个整式为,第二个整式为,第二个整式减去第一个整式的差记为,将记为,将第二个整式加上作为第三个整式,将记为,将第三个整式与相加记为第四个整式,以此类推.以下结论正确的个数是( )
①;②当时,第四个整式的值为81;③若第三个整式与第四个整式的和为25,则;④第2023个整式为.
A.1 B.2 C.3 D.4
二、填空题
7.若多项式的结果是一个多项式的平方,则单项式 .(只填一个你认为正确的答案)
8.分解因式: .
9.因式分解:ax2﹣8ax+16a= .
10.如图,搭一个三角形需要根火柴,搭两个三角形需要根火柴,搭三个三角形需要根火柴,,按这个规律,搭个这样的三角形的需要火柴棒根数为 .
11.的个位数字是 .
12.观察下列等式:,,,,,,,,根据上述规律可得的结果的个位数字是 .
13.观察下列算式,你发现了什么规律?
(1)根据你发现的规律,计算下面算式的值:
(2)请用一个含n的算式表示这个规律: ;
14.若的积中,“”项的系数为,则 .
15.已知:a,b,c都是正整数,且,.abc的最大值为M,最小值为N,则 .
16.单项式的系数与次数的和是 .
17.计算: .
18.把多项式分解因式时,应提取的公因式是 .
三、解答题
19.计算:. 20.化简:
21.计算:.
22.先化简,再求值
(1)已知,求代数式的值.
(2)已知为正整数,且,求的值.
(3)若、满足,,求下列各式的值.
①;
②.
23.已知一个长方形的面积是,它的一边长为,用含a、b的式子表示长方形的另一边长.(需化简)
24.某农户去年承包荒山若干亩,投资17800元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元.该农户将水果拉到市场出售平均每天出售2000千克,需8人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天400元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若,元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到25000元,那么纯收入增长率是多少?(纯收入=总收入-总支出,该农户采用了(2)中较好的出售方式出售)
25.学校准备在植物园周围增设由大小相同的等边三角形组成的栅栏,当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图);当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图);当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形(如图)……
根据以上规律,解答下列问题:
(1)当栅栏顶部是个灰色等边三角形时,其余部分镂空的等边三角形的个数为_______.
(2)当栅栏顶部是个灰色等边三角形时,其余部分镂空的等边三角形的个数为_______.(用含的代数式表示)
(3)已知每个等边三角形的面积均为,如果学校植物园周围栅栏的总面积要达到,那么至少需要灰色等边三角形多少个?
26.【探究发现】
如图1,有型,型正方形卡片和型长方形卡片各若干张.
(1)由1张型卡片,2张型卡片,3张型卡片拼成一个长方形,如图2,用两种方法计算这个长方形面积,可以得到一个等式,请你写出这个等式_______________.
(2)选取1张型卡片,16张型卡片,________张型卡片,可以拼成一个正方形,这个正方形的边长用含,的式子表示为________.
【拓展提升】
(3)如图,正方形边长分别为,,已知,,求阴影部分的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6
答案 C D D B B C
1.C
【分析】本题考查了单项式的次数和系数:单项式的数字因数是单项式的系数、字母的指数之和为单项式的次数,据此即可作答.
【详解】解:单项式的系数和次数分别是,3
故选:C.
2.D
【分析】根据同底数幂的运算法则,合并同类项,完全平方公式,逐个进行判断即可.
【详解】解:A、,故A不正确,不符合题意;
B、,故B不正确,不符合题意;
C、,故C不正确,不符合题意;
D、,故D正确,符合题意;
故选:D.
【点睛】本题主要考查了同底数幂的运算法则,合并同类项以及完全平方公式,解题的关键是掌握同底数幂相乘(除),底数不变,指数相加(减);幂的乘方,底数不变,指数相乘;积的乘方,把每个因式分别乘方;合并同类项,字母和相同字母是指数不变,只把系数相加减.
3.D
【分析】本题主要考查有理数的混合运算,考查了学生的分析、总结、归纳能力,规律题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结一般性的规律.
【详解】解:令,
则,
∴,
∴,
即,
故选:D.
4.B
【分析】本题主要考查了幂的运算,合并同类项等.熟练掌握同底数幂乘法的法则,积的乘方法则,商的乘方法则,幂的乘方法则,合并同类项法则,根据同底数幂乘法的法则,积的乘方法则,商的乘方法则,幂的乘方法则,合并同类项法则,逐一判断.
【详解】解:A.,
∵,A正确,不符合题意;
B.,
∵,B错误,符合题意;
C.,
∵,C正确,不符合题意;
D.,
∵,D正确,不符合题意.
故选:B.
5.B
【分析】设小长方形的长为a cm,宽为b cm,底面大长方形的宽为xcm,长为(x+)cm,再结合图形分别得出图形②的阴影周长和图形③的阴影周长,比较后即可求出答案.
【详解】解:设小长方形的长为a cm,宽为b cm,大长方形的宽为xcm,长为(x+2)cm,
∴②阴影周长为:2(x+2+x)=4x+4,
∴③左下阴影部分的周长为:2(x-2b+x+2-2b),右上阴影部分的周长为:2(x+2-a+x-a),
∴总周长为:2(x-2b+x+2-2b)+2(x+2-a+x-a)=4(x+2)+4x-4(a+2b),
又∵a+2b=x+2,
∴4(x+2)+4x-4(a+2b)=4x,
∴C2-C3=4x+4-4x=4(cm).
故选:B
【点睛】此题主要考查整式的加减的运用,做此类题要善于观察,在第②个图形中利用割补法进行计算,很容易计算得出结果.
6.C
【分析】先求出前几项的值,再求出,,的值,找到它们的变化规律,再逐一判断求解
【详解】解:由题意得:第一个整式为:,第二个整式为:,
∴,
,
;故①正确;
∴第三个整式为
第四个整式为
∴当时,第四个整式的值为,故②正确;
第2023个整式为,故④正确;
若第三个整式与第四个整式的和为25,则,解得,故③错误;
综上分析可知,正确的有3个.
故选:C.
【点睛】本题考查了数字的变化类,找到数字的变化规律是解题的关键.
7.或(任填一个即可)
【分析】分当M为中间项时,当为中间项时,两种情况根据完全平方式的特点进行求解即可.
【详解】解:当M为中间项时,则,
∴;
当为中间项时,则,
∴;
综上所述,或,
故答案为:或(任填一个即可).
【点睛】本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.
8./
【分析】本题考查因式分解,先提公因式,再利用完全平方公式分解因式,即可解题.
【详解】解:,
故答案为:.
9.
【分析】先提内参因式a,再运用公式法分解即可.
【详解】解:ax2-8ax+16a=a(x2-8x+16)=a(x-4)2,
故答案为:a(x-4)2.
【点睛】本题考查提公因式法和运用公式法分解因式.先提公因式,再用公式分解是解题的关键.注意:因式分解要分解到不能再分解为止.
10./
【分析】根据图形得出每增加一个三角形就增加了根火柴棒,据此得出答案.
【详解】解:搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
搭个三角形需要火柴棒的根数为:,
故答案为:.
【点睛】本题主要考查图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
11.5
【分析】将原式乘以凑出平方差公式的形式,按照平方差公式进行计算即可得出答案.
【详解】解:
,
∵,,,,,
∴指数4个数一个循环,
∵
∴尾数为6,
∴个位数字是5.
故答案为:5.
【点睛】本题考查的是平方差公式,能够将原式乘以凑出平方差公式的形式是解题的关键.
12.
【分析】观察所给等式发现规律末位数字为:,,,,,,,,每4个数一组循环,进而可得算式:结果的个位数字.
【详解】解:观察下列等式:,,,,,,,,
发现规律:末位数字为:,,,,,,,,
每4个数一组循环,
所以,而,
所有个位数字之和是.
所以算式:的结果的个位数字是.
故答案为:.
【点睛】本题考查了规律型—数字的变化类,解决本题的关键是根据数字的变化寻找规律.
13.
【分析】本题考查了含有乘方的有理数的混合运算,整式的混合运算,根据材料提示,找出计算规律即可求解,
(1)根据材料提示,找出规律计算即可;
(2)由材料、(1)中的规律,整式的混合运算进行计算即可求解.
【详解】解:(1)根据材料提示可得,;
(2)根据材料提示可得,
故答案为: ①;②.
14.4
【分析】先计算多项式乘以多项式,然后根据的系数为5求解即可.
【详解】解:
,
∵的系数为5,
∴ ,
解得,
故答案为:4.
【点睛】本题主要考查了多项式乘以多项式,解题的关键在于能够熟练掌握相关多项式乘以多项式进行求解.
15.
【分析】由已知条件整理出,再利用因式分解法转化为求的正整数解,据此得到或或或,据此解得a的值,最后代入计算即可.
【详解】解:,
,
,
,
,
,
,
,,都是正整数,
或或或,
或或或,
或,
即的最大值为,最小值为,即,,
∴,
故答案为:.
【点睛】本题考查因式分解法、二元一次方程组的整数解等知识,是重要考点,掌握相关知识是解题关键.
16.1
【分析】本题考查的是单项式的系数和次数,根据单项式的系数和次数的概念分别求出单项式的系数和次数,根据有理数的加法法则计算即可.
【详解】解:单项式的系数是,次数是2,
则单项式的系数与次数和为:,
故答案为:1.
17.
【分析】先计算单项式乘多项式,然后在合并同类项即可.
【详解】解:原式
故答案为:.
【点睛】本题是对整式乘法的考查,熟练掌握整式乘法运算是解决本题的关键.
18.
【分析】公因式的确定,一看系数:若各项系数都是整数,应提取各项系数的最大公因数;二看字母:公因式的字母是各项相同的字母;三看字母的指数:各相同字母的指数取指数最低的.
【详解】解:的公因式为.
故答案为:.
【点睛】本题考查了公因式的定义,熟练掌握公因式的定义是解答本题的关键.一个多项式的各项都含有的相同的因式叫做这个多项式各项的公因式.
19.(1);(2)
【分析】(1)根据多项式除以单项式的运算法则计算即可;
(2)根据平方差公式,多项式乘以单项式计算即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查多项式除以单项式,平方差公式,多项式乘以单项式,正确计算是解题的关键.
20.
【分析】利用合并同类项化简即可.
【详解】解:原式=
=
【点睛】本题考查了整式的合并同类项,注意不是同类项不能合并.
21.(1)
(2)
(3)
【分析】(1)运用乘法运算律求解即可;
(2)先计算乘方运算及小括号中的运算,然后计算乘除运算,最后计算加减运算即可;
(2)直接合并同类项计算即可.
【详解】(1)解:
;
(2)
;
(3)
.
【点睛】题目主要考查有理数的混合运算及整式的加减运算,熟练掌握运算法则是解题关键.
22.(1)-1;
(2)32;
(3)①;②.
【分析】(1)根据完全平方公式化简后,再把代入计算即可;
(2)根据幂的乘方的运算法则化简后,把代入计算即可;
(3)根据完全平方公式求解即可.
【详解】(1),
;
(2),
;
(3)①,,
;
(3),,
.
【点睛】本题主要考查了整式的混合运算,幂的乘方以及完全平方公式,熟记相关公式与运算法则是解答本题的关键.
23.
【分析】本题考查多项式除以单项式.利用长方形的面积除以边长进行求解即可.
【详解】解:由题意,得:长方形的另一边长为.
24.(1)拉到市场出售的收入为元;在果园出售的收入为元
(2)选择在果园直接出售比较好
(3)增长率为
【分析】(1)市场出售收入水果的总收入额外支出,而水果直接在果园的出售收入为:元.
(2)根据(1)中得到的代数式,将,,代入代数式计算即可.
(3)根据(2)的数据,首先确定今年的最高收入,然后计算增长率即可.
【详解】(1)解:将这批水果拉到市场上出售收入为:
(元),
故在果园直接出售收入为:元;
(2)解:当时,市场收入为(元.
当时,果园收入为(元,
因,所以应选择在果园直接出售;
(3)解:因为今年的纯收入为(元),,
所以增长率为.
【点睛】本题考查了根据实际问题列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解题的关键是读懂题意,正确表达.
25.(1)
(2)
(3)至少需要灰色等边三角形个
【分析】本题考查了图形规律及一元一次方程的应用,以镂空的等边三角形和灰色镂空的等边三角形的拼图为背景,关键是掌握规律性问题的解决方法,探究规律要认真观察、仔细思考,善用联想来解决这类问题.
()观察第个图案可知:中间的一个灰色镂空的等边三角形对应个镂空的等边三角形,第个图案可知增加一个灰色镂空的等边三角形,变成了个镂空的等边三角形,增加了个镂空的等边三角形,从而据此规律即可得解;
()观察第个图案,有个镂空的等边三角形;第个图案,有个镂空的等边三角形;,依次计算可解答;
()由()中的规律可知:,解方程即可解答.
【详解】(1)解:当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
当栅栏顶部是个灰色等边三角形时,其余部分共个镂空的等边三角形;
故答案为:;
(2)解:第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
第个图案:镂空的等边三角形有:(个),
……
第个图案:镂空的等边三角形有:个,
故答案为:;
(3)解:,
,
按此规律镶嵌图案,需要灰色镂空的等边三角形个.
26.(1);(2)64;;(3)20
【分析】本题主要考查考查完全平方公式的几何意义,以及多项式乘以多项式玘几何图形的关系:
(1)用两种方法表示图2的面积,即可得出等式;
(2)由拼图可得是完全平方式,则,即,从而得出答案;
(3)表示阴影部分的面积,化成,再整体代入求值即可.
【详解】解:方法1:大长方形的面积为,
方法2:图2中五部分的面积和为:,
因此有;
故答案为:;
(2)由面积拼图可知,
故答案为:64,;
(3)由图形面积之间的关系可得,
.
∵,,
∴原式
故答案为:20
答案第1页,共2页
答案第1页,共2页
同课章节目录
