青岛版(六三制)数学八年级上册 5.6几何证明举例教案(共4课时)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 5.6几何证明举例教案(共4课时) |  | |
| 格式 | doc | ||
| 文件大小 | 96.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-02 22:32:19 | ||
图片预览




文档简介
几何证明举例
【课时安排】
4课时
【第一课时】
【教学目标】
1.证明并掌握“AAS”定理;会用“AAS”定理解决有关的问题。
2.知道全等三角形的性质:对应角平分线相等,对应中线相等,对应高相等;
并会证明这些结论。
3.掌握几何证明题思路、及命题证明的一般步骤和规范书写格式。
4.增强合作意识,提高逻辑思维能力,养成良好的学习习惯。
【教学重难点】
1.证明并掌握“AAS”定理;会用“AAS”定理解决有关的问题。
2.掌握几何证明题思路、及命题证明的一般步骤和规范书写格式。
【教学过程】
(一)前置练习,积累知识。
(1)全等三角形的性质:全等三角形的_____相等,_____相等。
(2)判定两个三角形全等的方法:_____、_____、_____、_____,其中_____、_____、_____都已作为基本事实。
(3)几何证明的过程一般包括三个步骤:_____,_____,_____。
知识点1:“AAS”定理:两角分别相等且其中一组等角的_____也相等的三角形全等。
知识点2:适当地添加辅助线:例1,通过添加辅助线构造两个_____三角形。
知识点3:全等三角形的性质:对应角平分线_____,对应中线_____,对应高_____。
(二)情境激趣,导入新课。
证明“AAS”定理:
两角分别________且其中一组等角的________也相等的三角形全等。
问题:
1.这个命题的条件是________________,结论是________________。
2.能根据题意画出题目中用到的图形吗?
3.能据图形和条件,把命题的条件用数学语言写成已知吗?把结论写成求证吗?
4.已知一边相等,再知道条件_____________可以用SSS来说明;或可以知道条件_______可以用ASA来说明全等。题目当中符合这两种判定方法吗?能根据题目已知两角对应相等,求出另外一个角相等,这样可以选择方法____________来证明。能总结证明“命题问题”的题目的一般步骤吗?_________________________。
(三)自主学习,合作探究。
1.典例精析
阅读课本例1,然后完成下列问题:
问题:图中有三角形吗?有全等三角形吗?已知什么条件可推全等?
已知:______________________
求证:______________________
证明:______________________
证明全等三角形对应边上的高相等,其他课下完成。
2.针对性训练,
(1)两个三角形只有以下元素对应相等,不能判定两个三角形全等的是( )
A.两角和一边 B.两边及夹角 C.三个角 D.三条边
(2)如图,△ABC中,AB=AC,AD⊥BC,点E、F分别是BD、DC的中点,
则图中全等三角形共有( )
A.3对 B.4对 C.5对 D.6对
(3)已知:如图:DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
(4)已知:如图,AB=AC,BDAC,CEAB,垂足分别为D、E,BD、CE相交于点F。
求证:BE=CD
(四)归纳总结,提升能力。
(五)当堂检测,检查效果。
1.如下图,已知AD=BC,要证明ΔABC≌ΔBAD,根据“SSS”,还需要一个条件___________,根据“SAS”,还需要一个条件________________。
2.如图,点O是AB的中点,AC∥BD,则ΔAOC≌ΔBOD的理由是___________。
3.如图,AB=AD,BE=DE,∠1=∠2,则图中全等三角形共有_____对。
4.已知:如图,点A.C.B在一条线上,且AC=EC,DC=BC,∠ACE=∠DCB。
求证:(1)△ACD≌△ECB;(2)AD=EB。
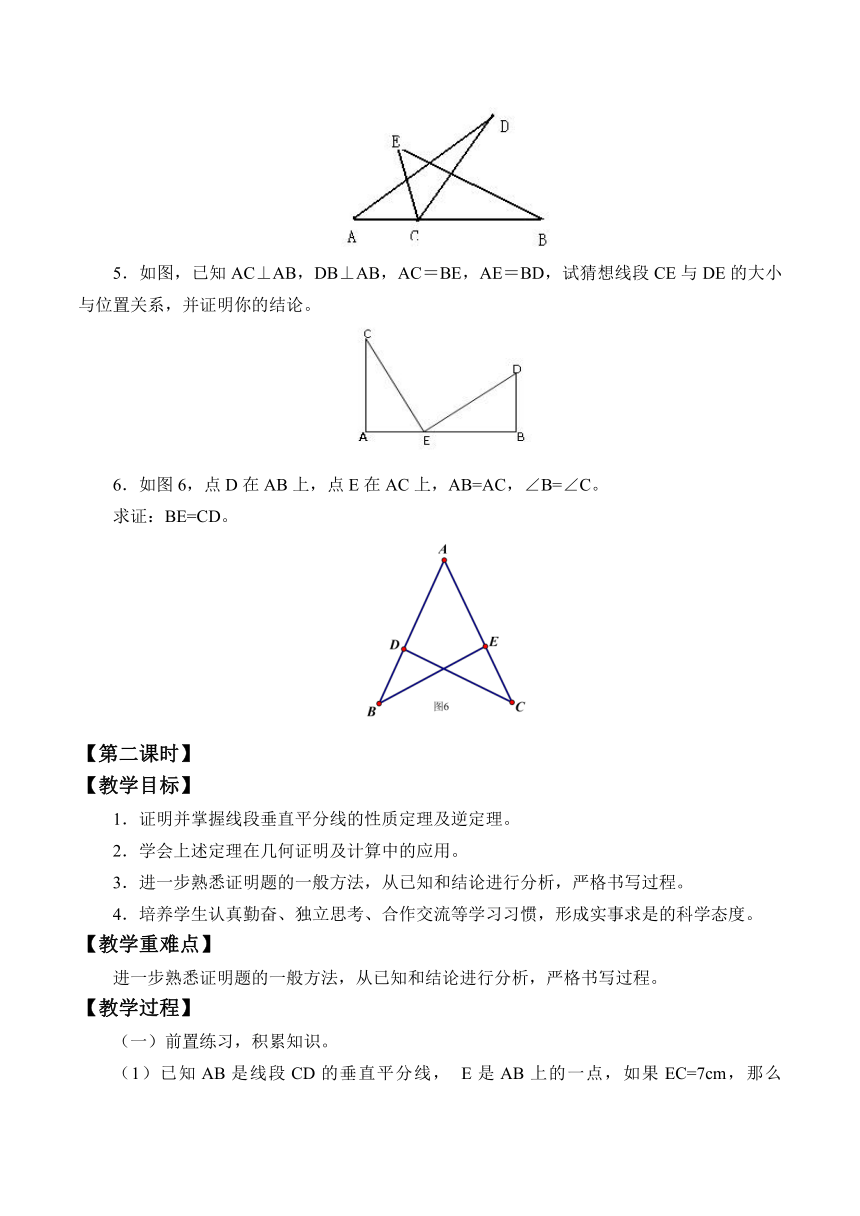
5.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论。
6.如图6,点D在AB上,点E在AC上,AB=AC,∠B=∠C。
求证:BE=CD。
【第二课时】
【教学目标】
1.证明并掌握线段垂直平分线的性质定理及逆定理。
2.学会上述定理在几何证明及计算中的应用。
3.进一步熟悉证明题的一般方法,从已知和结论进行分析,严格书写过程。
4.培养学生认真勤奋、独立思考、合作交流等学习习惯,形成实事求是的科学态度。
【教学重难点】
进一步熟悉证明题的一般方法,从已知和结论进行分析,严格书写过程。
【教学过程】
(一)前置练习,积累知识。
(1)已知AB是线段CD的垂直平分线, E是AB上的一点,如果EC=7cm,那么ED=______cm;如果∠ECD=60°,那么∠EDC=_______°。
(2)已知A和B两点在线段EF的垂直平分线上,且∠EAF=100°,∠EBF=70°,则∠AEB=( )
A.95° B.15° C.95°或15° D.170°或30°
(二)情景激趣,导入新课。
我们学了线段垂直平分线的性质和判定,你能证明它们吗?
(三)自主学习,合作探究。
1.预习检查
(1)线段是轴对称图形,它的对称轴是____________________。
(2)线段垂直平分线的性质及的逆命题是____________,逆命题是______命题。
2.典例精析
☆探究一:证明线段垂直平分线的性质定理
已知:直线_______是线段AB的垂直平分线,垂足为点_____。
点P是直线______上的任意一点。
求证:______=_______
证明:(1)当点____不与线段的中点M重合时。
∵CD⊥AB(已知)
∴∠_____=∠_____=90°(垂直平分线的定义)
∵PM=PM( ) MA=_____(垂直平分线的定义)
∴△APM≌△________( )
∴PA=PB( )
(2)当点_______与线段的中点M重合时。
∵MA=MB(垂直平分线的定义)
∴PA=PB( )
☆探究二:证明线段垂直平分线的性质定理的逆定理:
到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上。
学生先组交流后独立完成证明过程,师适时补充。并找代表展示。
3.针对性练习
(1)如图,△ABC中,AB=AC,DE是AB的垂直平分线AB=8,BC=4,∠A=36°,则∠DBC=_______,△BDC的周长等于_______。
(2)已知:如图,在Rt△ABC中,∠A=90°,AB=3,AC=5,BC边上的垂直平分线DE交BC于点D,交AC于点E,求△ABE的周长。
(四)归纳总结,能力提升。
1.学会了:(知识点、思想方法等)__________________________________;
2.不太懂的地方:__________________________________。
(五)当堂检测,检查效果。
2.如果三角形两边的垂直平分线的交点恰好落在第三边上,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.已知:如图,AB=AD,BC=DC,E是AC上一点,求证:BE=DE
4.如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.
求∠PAQ的度数。
【作业布置】
1.必做题:第8、9题;
2.选做题:第12题。
预分线的性质定理和判定定理。
【第三课时】
【教学目标】
1.证明并掌握角平分线的性质定理及逆定理。
2.会用上述定理证明有关的命题。
3.知道证明要合乎逻辑,知道证明的过程可以有不同的表达形式,学会综合法证明的格式。
4.养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯,形成实事求是的科学态度。
【教学重难点】
1.证明并掌握角平分线的性质定理及逆定理。
2.会用上述定理证明有关的命题。
3.知道证明要合乎逻辑,知道证明的过程可以有不同的表达形式,学会综合法证明的格式。
【教学过程】
(一)前置练习,积累知识。
1.相关知识链接
(1)角平分线的定义:__________________________________。
(2)∠AOB的平分线上一点M,M到OA的距离为2cm,则M到OB的距离为_________。
(3)判定两个三角形全等的方法有:______________________________________。
2.知识点1:角平分线的性质定理:角平分线上的点,到这个角的________________________相等。
知识点2:角平分线的性质定理的逆定理:角的内部到角的___________相等的点在这个角的平分线上。
知识点3:证明三角形三条角平分线交于一点(内心)
(二)情境激趣,导入新课。
(三)自主学习,合作探究。
☆探究一:角平分线的性质定理的证明(学生自学课本内容,教师点拨。)
已知:如图,射线______是∠ABC的平分线,点P在BD上,______⊥A,______⊥BC,垂足分别是点______和______。
求证:______=______
证明:(用“∵、∴”的格式写出证明过程。)
定理归纳:
☆探究二:证明角平分线的性质定理的逆定理(即角平分线的判定定理)
问题:(1)角平分线的性质定理的逆命题是____________________,
逆命题的条件是____________________结论是____________________。
(2)要证明三角形的三条角平分线交于一点,只要证明两条角平分线的交点也在____________________上就可以了。
已知:____________________
求证:____________________
证明:____________________
定理归纳:
☆探究三:证明三角形三条角平分线交于一点(内心)
已知:____________________
求证:____________________
证明:____________________
结论:三角形的三条角平分线交于______点,并且这一点到三条边的距离______。
引申:三角形的三条角平分线交于一点,若设这一点到其中一边的距离为m,三边长分别为a、b、c,则三角形的面积S=______。
课堂练习:
1.Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,AB=8cm,则DE+DC=______cm。
2.已知:如图,已知AD为△ABC的角平分线,∠B=90°,DF⊥AC,垂足为F,DE=DC.
求证:BE=CF
(四)归纳总结,提升能力。
1.学会了:(知识点、思想方法、学习习惯等。)
2.不太懂的地方:______
3.今后努力的方向:______
(五)当堂检测,检查效果。
1.已知:△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,且交于P,若P到边AB的距离为3cm,△ABC的周长为18cm,则△ABC的面积为______。
2.到三角形三边距离相等的点是( )
A.三条中线的交点 B.三条高的交点 C.三条角平分线的交点 D.不能确定
3.已知:OP是∠MON内的一条射线,AC⊥OM,AD⊥ON,BE⊥OM,BF⊥ON,垂足分别为C、D、E、F,且AC=AD.
求证:BE=BF
4.如图,∠C=900,AC=BC,AD是∠BAC的角平分线。
求证:AC+CD=AB
【第四课时】
【教学目标】
1.进一步熟悉证明题的题型,掌握判定直角三角形全等的斜边、直角边判定定理。
2.在已知一直角边和斜边的条件下,会用尺规作图的方法作直角三角形。
3.能够运用斜边、直角边判定定理及其它三角形全等的判定方法进行证明。
4.增强学生的合作意识,提高学生的逻辑思维能力。
【教学重难点】
1.在已知一直角边和斜边的条件下,会用尺规作图的方法作直角三角形。
2.能够运用斜边、直角边判定定理及其它三角形全等的判定方法进行证明。
【教学过程】
(一)前置练习,积累知识。
1.若∠A=∠D,AB=DE,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据_____(简写)。
2.若∠A=∠D,BC=EF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据_____(简写)。
3.若AB=DE,BC=EF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据______(简写)。
4.若AB=DE,BC=EF,AC=DF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据______(简写)。
思考交流:判定两个直角三角形全等,有哪些方法?
(1)三角形的内角和定理:三角形三个内角的和等于______。
(2)有一个角是______角的三角形叫做直角三角形,它通常用符号______表示。
(3)命题“直角三角形的两个锐角互余”的条件是______,结论是______;它是______命题(填“真”“假”)。
(二)情境激趣,导入新课。
学生读课本:交流与发现(2)后,书写Rt△ABC与Rt△A′B′C′全等的证明过程。
总结:直角三角形全等的判定定理__________________________________________
这个定理可以简单地计作“__________________”或“___________________”。
学生交流课本:交流与发现(3),得出结论___________________
对于创设情境、引入新课中的问题:如果AB=DE,AC=DF,那么两个直角三角形是否全等?说明理由。
总结:直角三角形两边对应相等,如果两边都是直角边,根据_______证明全等;如果两边是一条直角边和一条斜边,根据___________________来说明另一边也相等,根据_______证明全等,也可以直接根据________证明全等。
(三)自主学习,合作探究。
1.如图CD⊥AD,CB⊥AB,AB=AD.
求证:CD=CB
2.已知:如图12,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,,AE=CF。
求证:(1);(2)。
(四)总结归纳,提升能力。
回顾本节课所学内容,教师作补充。
(五)当堂检测,检查效果。
1.如图:Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交与点O,则有_______≌_______,判定的根据是_______。还有_______≌_______判断的根据是_______。
2.已知:如图,AB=CD,DE⊥AC于E点,BF⊥AC于F,且AE=CF,∠D=60°。
求:∠A的度数。
3.已知:如图,BE,CF为△ABC的高,且BE=CF,BE,CF交于H点。
求证:AB=AC
【课时安排】
4课时
【第一课时】
【教学目标】
1.证明并掌握“AAS”定理;会用“AAS”定理解决有关的问题。
2.知道全等三角形的性质:对应角平分线相等,对应中线相等,对应高相等;
并会证明这些结论。
3.掌握几何证明题思路、及命题证明的一般步骤和规范书写格式。
4.增强合作意识,提高逻辑思维能力,养成良好的学习习惯。
【教学重难点】
1.证明并掌握“AAS”定理;会用“AAS”定理解决有关的问题。
2.掌握几何证明题思路、及命题证明的一般步骤和规范书写格式。
【教学过程】
(一)前置练习,积累知识。
(1)全等三角形的性质:全等三角形的_____相等,_____相等。
(2)判定两个三角形全等的方法:_____、_____、_____、_____,其中_____、_____、_____都已作为基本事实。
(3)几何证明的过程一般包括三个步骤:_____,_____,_____。
知识点1:“AAS”定理:两角分别相等且其中一组等角的_____也相等的三角形全等。
知识点2:适当地添加辅助线:例1,通过添加辅助线构造两个_____三角形。
知识点3:全等三角形的性质:对应角平分线_____,对应中线_____,对应高_____。
(二)情境激趣,导入新课。
证明“AAS”定理:
两角分别________且其中一组等角的________也相等的三角形全等。
问题:
1.这个命题的条件是________________,结论是________________。
2.能根据题意画出题目中用到的图形吗?
3.能据图形和条件,把命题的条件用数学语言写成已知吗?把结论写成求证吗?
4.已知一边相等,再知道条件_____________可以用SSS来说明;或可以知道条件_______可以用ASA来说明全等。题目当中符合这两种判定方法吗?能根据题目已知两角对应相等,求出另外一个角相等,这样可以选择方法____________来证明。能总结证明“命题问题”的题目的一般步骤吗?_________________________。
(三)自主学习,合作探究。
1.典例精析
阅读课本例1,然后完成下列问题:
问题:图中有三角形吗?有全等三角形吗?已知什么条件可推全等?
已知:______________________
求证:______________________
证明:______________________
证明全等三角形对应边上的高相等,其他课下完成。
2.针对性训练,
(1)两个三角形只有以下元素对应相等,不能判定两个三角形全等的是( )
A.两角和一边 B.两边及夹角 C.三个角 D.三条边
(2)如图,△ABC中,AB=AC,AD⊥BC,点E、F分别是BD、DC的中点,
则图中全等三角形共有( )
A.3对 B.4对 C.5对 D.6对
(3)已知:如图:DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
(4)已知:如图,AB=AC,BDAC,CEAB,垂足分别为D、E,BD、CE相交于点F。
求证:BE=CD
(四)归纳总结,提升能力。
(五)当堂检测,检查效果。
1.如下图,已知AD=BC,要证明ΔABC≌ΔBAD,根据“SSS”,还需要一个条件___________,根据“SAS”,还需要一个条件________________。
2.如图,点O是AB的中点,AC∥BD,则ΔAOC≌ΔBOD的理由是___________。
3.如图,AB=AD,BE=DE,∠1=∠2,则图中全等三角形共有_____对。
4.已知:如图,点A.C.B在一条线上,且AC=EC,DC=BC,∠ACE=∠DCB。
求证:(1)△ACD≌△ECB;(2)AD=EB。
5.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论。
6.如图6,点D在AB上,点E在AC上,AB=AC,∠B=∠C。
求证:BE=CD。
【第二课时】
【教学目标】
1.证明并掌握线段垂直平分线的性质定理及逆定理。
2.学会上述定理在几何证明及计算中的应用。
3.进一步熟悉证明题的一般方法,从已知和结论进行分析,严格书写过程。
4.培养学生认真勤奋、独立思考、合作交流等学习习惯,形成实事求是的科学态度。
【教学重难点】
进一步熟悉证明题的一般方法,从已知和结论进行分析,严格书写过程。
【教学过程】
(一)前置练习,积累知识。
(1)已知AB是线段CD的垂直平分线, E是AB上的一点,如果EC=7cm,那么ED=______cm;如果∠ECD=60°,那么∠EDC=_______°。
(2)已知A和B两点在线段EF的垂直平分线上,且∠EAF=100°,∠EBF=70°,则∠AEB=( )
A.95° B.15° C.95°或15° D.170°或30°
(二)情景激趣,导入新课。
我们学了线段垂直平分线的性质和判定,你能证明它们吗?
(三)自主学习,合作探究。
1.预习检查
(1)线段是轴对称图形,它的对称轴是____________________。
(2)线段垂直平分线的性质及的逆命题是____________,逆命题是______命题。
2.典例精析
☆探究一:证明线段垂直平分线的性质定理
已知:直线_______是线段AB的垂直平分线,垂足为点_____。
点P是直线______上的任意一点。
求证:______=_______
证明:(1)当点____不与线段的中点M重合时。
∵CD⊥AB(已知)
∴∠_____=∠_____=90°(垂直平分线的定义)
∵PM=PM( ) MA=_____(垂直平分线的定义)
∴△APM≌△________( )
∴PA=PB( )
(2)当点_______与线段的中点M重合时。
∵MA=MB(垂直平分线的定义)
∴PA=PB( )
☆探究二:证明线段垂直平分线的性质定理的逆定理:
到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上。
学生先组交流后独立完成证明过程,师适时补充。并找代表展示。
3.针对性练习
(1)如图,△ABC中,AB=AC,DE是AB的垂直平分线AB=8,BC=4,∠A=36°,则∠DBC=_______,△BDC的周长等于_______。
(2)已知:如图,在Rt△ABC中,∠A=90°,AB=3,AC=5,BC边上的垂直平分线DE交BC于点D,交AC于点E,求△ABE的周长。
(四)归纳总结,能力提升。
1.学会了:(知识点、思想方法等)__________________________________;
2.不太懂的地方:__________________________________。
(五)当堂检测,检查效果。
2.如果三角形两边的垂直平分线的交点恰好落在第三边上,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.已知:如图,AB=AD,BC=DC,E是AC上一点,求证:BE=DE
4.如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.
求∠PAQ的度数。
【作业布置】
1.必做题:第8、9题;
2.选做题:第12题。
预分线的性质定理和判定定理。
【第三课时】
【教学目标】
1.证明并掌握角平分线的性质定理及逆定理。
2.会用上述定理证明有关的命题。
3.知道证明要合乎逻辑,知道证明的过程可以有不同的表达形式,学会综合法证明的格式。
4.养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯,形成实事求是的科学态度。
【教学重难点】
1.证明并掌握角平分线的性质定理及逆定理。
2.会用上述定理证明有关的命题。
3.知道证明要合乎逻辑,知道证明的过程可以有不同的表达形式,学会综合法证明的格式。
【教学过程】
(一)前置练习,积累知识。
1.相关知识链接
(1)角平分线的定义:__________________________________。
(2)∠AOB的平分线上一点M,M到OA的距离为2cm,则M到OB的距离为_________。
(3)判定两个三角形全等的方法有:______________________________________。
2.知识点1:角平分线的性质定理:角平分线上的点,到这个角的________________________相等。
知识点2:角平分线的性质定理的逆定理:角的内部到角的___________相等的点在这个角的平分线上。
知识点3:证明三角形三条角平分线交于一点(内心)
(二)情境激趣,导入新课。
(三)自主学习,合作探究。
☆探究一:角平分线的性质定理的证明(学生自学课本内容,教师点拨。)
已知:如图,射线______是∠ABC的平分线,点P在BD上,______⊥A,______⊥BC,垂足分别是点______和______。
求证:______=______
证明:(用“∵、∴”的格式写出证明过程。)
定理归纳:
☆探究二:证明角平分线的性质定理的逆定理(即角平分线的判定定理)
问题:(1)角平分线的性质定理的逆命题是____________________,
逆命题的条件是____________________结论是____________________。
(2)要证明三角形的三条角平分线交于一点,只要证明两条角平分线的交点也在____________________上就可以了。
已知:____________________
求证:____________________
证明:____________________
定理归纳:
☆探究三:证明三角形三条角平分线交于一点(内心)
已知:____________________
求证:____________________
证明:____________________
结论:三角形的三条角平分线交于______点,并且这一点到三条边的距离______。
引申:三角形的三条角平分线交于一点,若设这一点到其中一边的距离为m,三边长分别为a、b、c,则三角形的面积S=______。
课堂练习:
1.Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,AB=8cm,则DE+DC=______cm。
2.已知:如图,已知AD为△ABC的角平分线,∠B=90°,DF⊥AC,垂足为F,DE=DC.
求证:BE=CF
(四)归纳总结,提升能力。
1.学会了:(知识点、思想方法、学习习惯等。)
2.不太懂的地方:______
3.今后努力的方向:______
(五)当堂检测,检查效果。
1.已知:△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,且交于P,若P到边AB的距离为3cm,△ABC的周长为18cm,则△ABC的面积为______。
2.到三角形三边距离相等的点是( )
A.三条中线的交点 B.三条高的交点 C.三条角平分线的交点 D.不能确定
3.已知:OP是∠MON内的一条射线,AC⊥OM,AD⊥ON,BE⊥OM,BF⊥ON,垂足分别为C、D、E、F,且AC=AD.
求证:BE=BF
4.如图,∠C=900,AC=BC,AD是∠BAC的角平分线。
求证:AC+CD=AB
【第四课时】
【教学目标】
1.进一步熟悉证明题的题型,掌握判定直角三角形全等的斜边、直角边判定定理。
2.在已知一直角边和斜边的条件下,会用尺规作图的方法作直角三角形。
3.能够运用斜边、直角边判定定理及其它三角形全等的判定方法进行证明。
4.增强学生的合作意识,提高学生的逻辑思维能力。
【教学重难点】
1.在已知一直角边和斜边的条件下,会用尺规作图的方法作直角三角形。
2.能够运用斜边、直角边判定定理及其它三角形全等的判定方法进行证明。
【教学过程】
(一)前置练习,积累知识。
1.若∠A=∠D,AB=DE,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据_____(简写)。
2.若∠A=∠D,BC=EF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据_____(简写)。
3.若AB=DE,BC=EF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据______(简写)。
4.若AB=DE,BC=EF,AC=DF,则Rt△ABC与Rt△DEF_____(填“全等”或“不全等”)根据______(简写)。
思考交流:判定两个直角三角形全等,有哪些方法?
(1)三角形的内角和定理:三角形三个内角的和等于______。
(2)有一个角是______角的三角形叫做直角三角形,它通常用符号______表示。
(3)命题“直角三角形的两个锐角互余”的条件是______,结论是______;它是______命题(填“真”“假”)。
(二)情境激趣,导入新课。
学生读课本:交流与发现(2)后,书写Rt△ABC与Rt△A′B′C′全等的证明过程。
总结:直角三角形全等的判定定理__________________________________________
这个定理可以简单地计作“__________________”或“___________________”。
学生交流课本:交流与发现(3),得出结论___________________
对于创设情境、引入新课中的问题:如果AB=DE,AC=DF,那么两个直角三角形是否全等?说明理由。
总结:直角三角形两边对应相等,如果两边都是直角边,根据_______证明全等;如果两边是一条直角边和一条斜边,根据___________________来说明另一边也相等,根据_______证明全等,也可以直接根据________证明全等。
(三)自主学习,合作探究。
1.如图CD⊥AD,CB⊥AB,AB=AD.
求证:CD=CB
2.已知:如图12,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,,AE=CF。
求证:(1);(2)。
(四)总结归纳,提升能力。
回顾本节课所学内容,教师作补充。
(五)当堂检测,检查效果。
1.如图:Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交与点O,则有_______≌_______,判定的根据是_______。还有_______≌_______判断的根据是_______。
2.已知:如图,AB=CD,DE⊥AC于E点,BF⊥AC于F,且AE=CF,∠D=60°。
求:∠A的度数。
3.已知:如图,BE,CF为△ABC的高,且BE=CF,BE,CF交于H点。
求证:AB=AC
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
