第七章 随机变量及其分布 小结 课件（共22张PPT）--2024-2025学年高中《数学》·选择性必修第三册人教A版

(共22张PPT)
第七章 随机变量及其分布 小结
主讲教师：
学 校：
年 级：高二年级
学 科：高中数学（人教A版）
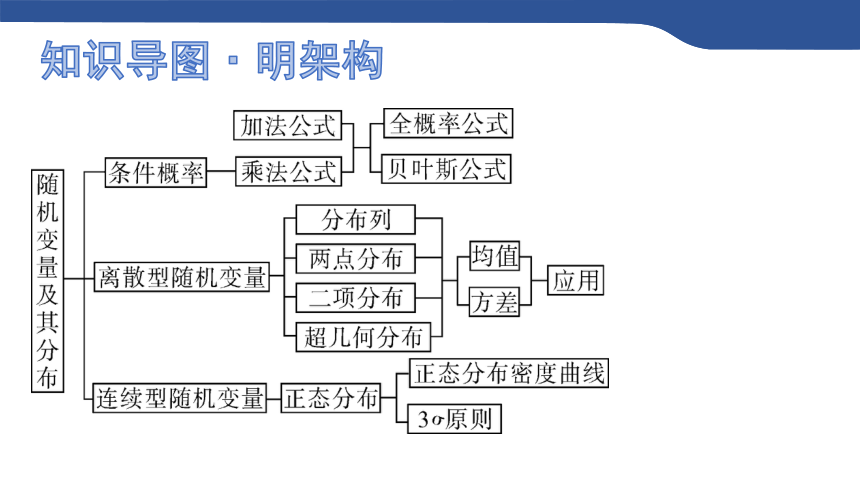
知识导图·明架构
问题 1 通过本章中“条件概率与全概率公式”学习，请思考：
（1）两个随机事件的独立性和条件概率有什么关系？
（2）用全概率公式求一个复杂事件的概率的思路是什么？
题型探究·悟思路
条件概率
全概率公式
*贝叶斯公式
试一试 1.（2014·全国高考（理））某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是 ( )
A．0.8 B．0.75 C．0.6 D．0.45
题型探究·悟思路
问题 2 结合本章的学习，请思考:
（1）离散型随机变量的分布列与样本频率分布有什么联系与区别？
（2）离散型随机变量的均值与方差的意义和作用是什么？它们与随机变量的观测值的平均值和方差的联系与区别是什么？
D
C
例1 [2022·全国甲卷] 甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局.三个项目比赛结束后，总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为 ， ， ，各项目的比赛结果相互独立.
（1）求甲学校获得冠军的概率；
（2）用 表示乙学校的总得分，求 的分布列与期望.
解： 记“甲学校获得冠军”为事件 ，则
故甲学校获得冠军的概率是0.6.
（2） 的所有可能取值为0，10，20，30，则
，
，
，
，所以 的分布列为
.
0 10 20 30
0.16 0.44 0.34 0.06
方法总结 求离散型随机变量的均值、方差的步骤：
（1）明确随机变量的取值，以及取每个值的试验结果；
（2）求出随机变量取各个值相对应的概率；
（3）列出分布列；
用期望、方差公式求解.
问题 3 本章中介绍了哪些分布列模型，并思考下列问题：
（1）归纳二项分布模型的特征，有人说“随机掷一枚质地均匀的硬币，出现正面的概率是0.5，因此，随机抛掷100次硬币，出现50次正面的可能性应该也是 0.5”你认为正确吗？为什么？
问题 3 本章中介绍了哪些分布列模型，并思考下列问题：
（2）离散型随机变量的分布规律与服从正态分布的随机变量的分布规律的区别是什么？
连续性随机变量的正态分布，随机变量的取值不能一 一列举，而且在任意单点值的概率都是 0.
C
D
B
例2 2024年五一期间，银泰百货举办了一次有奖促销活动，消费每超过600元(含600元)，均可抽奖一次，抽奖方案有两种，顾客只能选择其中的一种.方案一：从装有10个形状、大小完全相同的小球(其中红球2个，白球1个，黑球7个)的抽奖盒中，一次性摸出3个球其中奖规则为：若摸到2个红球和1个白球，享受免单优惠；若摸出2个红球和1个黑球则打5折；若摸出1个白球2个黑球，则打7折；其余情况不打折.方案二：从装有10个形状、大小完全相同的小球(其中红球3个，黑球7个)的抽奖盒中，有放回每次摸取1球，连摸3次，每摸到1次红球，立减200元.
（1）若两个顾客均分别消费了600元，且均选择抽奖方案一，试求两位顾客均享受免单优惠的概率；
（2）若某顾客消费恰好满1000元，试从概率角度比较该顾客选择哪一种抽奖方案更合算？
归纳小结·定乾坤
1.条件概率及全概率
2.离散型随机变量及分布列
3.离散型随机变量的数字特征
4.二项分布、超几何分布与正态分布
拓展延伸·育素养
课外阅读： 高尔顿板
弗朗西斯·高尔顿（ ， —1911）是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟，虽然不像达尔文那样声名显赫，但也不是无名之辈.并且，高尔顿幼年是神童，长大是才子，九十年的人生丰富多彩，是个名副其实的博学家.他涉猎范围广泛，研究水平颇深，纵观科学史，在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等，还有与社会有关的人类学、民族学、教育学、宗教学，以及优生学、指纹学、照相术、登山术等等.