初中数学人教版九年级上册 22.1.2 二次函数的图像和性质 教学设计(表格式)
文档属性
| 名称 | 初中数学人教版九年级上册 22.1.2 二次函数的图像和性质 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 662.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-03 00:00:00 | ||
图片预览

文档简介
教 学 设 计
教学内容:二次函数的图像和性质
教 材 分 析
素 养 目 标 用描点法画二次函数 的图像,知道抛物线 是轴对称对称图形,知道抛物线的开口方向与a的符号有关 掌握二次函数 的性质:开口方向、对称轴、顶点坐标、变化趋势。
教学重难点 重点:画二次函数 图像,掌握二次函数 性质 难点:根据a的符号说出顶点是抛物线的最高点还是最低点,性质的推导过程
教 学 方 法 探究法、总结法、讲授法
教 学 资 源 课件
教 学 流 程
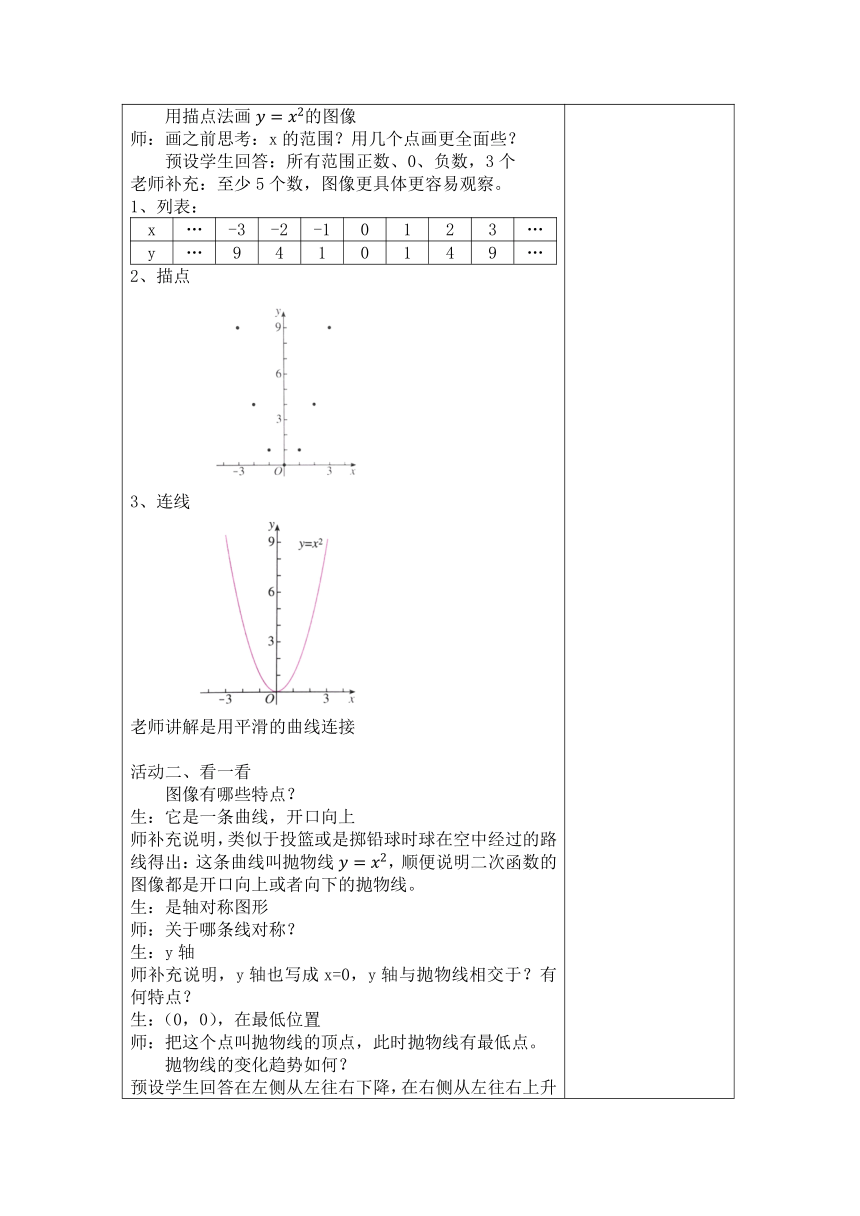
一、教学过程 一)、复习导入 1、二次函数的一般形式是怎样的? (a、b、c是常数,a≠0) 2、下列函数中,哪些是二次函数? y=x ②y=x - ③y=x-x ④y=x + -1 ⑤y=x +2x-4 ③ ⑤ 一次函数的图像是什么? 一条直线 4、通常怎样画一个函数的图像? 描点法:列表、描点、连线 本节课来学习最简单的二次函数的图像 设计意图:巩固上节课学习的二次函数的概念,过度到学它的图像和性质,其中讲到一次函数的图像研究方法,为的是让学生在他们熟悉的知识上引发思考,探究新知。 二)、新授 活动一、画一画 用描点法画的图像 师:画之前思考:x的范围?用几个点画更全面些? 预设学生回答:所有范围正数、0、负数,3个 老师补充:至少5个数,图像更具体更容易观察。 1、列表: x…-3-2-10123…y…9410149…
2、描点 3、连线 老师讲解是用平滑的曲线连接 活动二、看一看 图像有哪些特点? 生:它是一条曲线,开口向上 师补充说明,类似于投篮或是掷铅球时球在空中经过的路线得出:这条曲线叫抛物线,顺便说明二次函数的图像都是开口向上或者向下的抛物线。 生:是轴对称图形 师:关于哪条线对称? 生:y轴 师补充说明,y轴也写成x=0,y轴与抛物线相交于?有何特点? 生:(0,0),在最低位置 师:把这个点叫抛物线的顶点,此时抛物线有最低点。 抛物线的变化趋势如何? 预设学生回答在左侧从左往右下降,在右侧从左往右上升 师引导补充:在a=1即a>0的前提下,左右侧的x、y从左往右分别如何变化? 得出它的变化趋势:a>0,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 活动三、练一练 画y=x 、的图像 三个图像对比有何异同? 1、a>0,开口向上、对称轴是y轴、顶点是原点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大 2、a越大,抛物线的开口越小 活动四、想一想 当a<0时,二次函数的图像和性质? 画、y=x 、的图像 1、一般地,当a<0时,抛物线的开口向下、对称轴是y轴、顶点是原点即抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小 2、a越小,抛物线的开口越小 总的概括:抛物线的对称轴是y轴、顶点是原点, 当a>0时,抛物线的开口向上、顶点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 当a<0时,抛物线的开口向下、顶点是抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小。 |a|越大,抛物线的开口越小。 设计意图:通过画图及观察发现,学生自己总结得出结论,新知更容易理解和消化。类比方法同样的道理,还能对比记忆,整体探究过程体现学生主体性。 三)、巩固练习 书32页:说出抛物线的开口方向、对称轴、顶点 ② ③y=x ④y=x 画 、y=x 的图形
板 书 设 计
二次函数的图像和性质 二次函数的图像是一条抛物线 二次函数的图像性质: 抛物线的对称轴是y轴、顶点是原点 当a>0时,抛物线的开口向上、顶点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 当a<0时,抛物线的开口向下、顶点是抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小。 |a|越大,抛物线的开口越小。
作 业 分 层 设 计
书41页第三题、第四题 画函数图像: 、 、y=x 写出抛物线 、y=x 的开口方向、对称轴、顶点 选做题: 若A(x1,y1),(x2,y2)在y=x 这条抛物线上,且x1<x2<0,则y1____y2.
教 学 反 思
本节课学习二次函数的图像和性质。导入部分,复习巩固上节课学习的二次函数的概念,过度到学它的图像和性质,其中讲到一次函数的图像研究方法,为的是让学生在他们熟悉的知识上引发思考,探究新知。在新授的过程当中,设计四个活动来进行教学:如何画一画二次函数的(a>0)的图像、看一看此的二次函数的图像有何特点、练一练同学们是否掌握此二次函数的画法、想一想当 a<0时,二次函数的图像和性质?类比讨论,对比出两者的异同,更容易记忆,整体探究过程体现学生主体性。当然过程中的不足是探究的东西多,对于时间上的把控有所欠缺。加上同学们可能在实际画图操作的过程中不是特别熟练,所以新课的内容没办法在现有的时间内完成。
教学内容:二次函数的图像和性质
教 材 分 析
素 养 目 标 用描点法画二次函数 的图像,知道抛物线 是轴对称对称图形,知道抛物线的开口方向与a的符号有关 掌握二次函数 的性质:开口方向、对称轴、顶点坐标、变化趋势。
教学重难点 重点:画二次函数 图像,掌握二次函数 性质 难点:根据a的符号说出顶点是抛物线的最高点还是最低点,性质的推导过程
教 学 方 法 探究法、总结法、讲授法
教 学 资 源 课件
教 学 流 程
一、教学过程 一)、复习导入 1、二次函数的一般形式是怎样的? (a、b、c是常数,a≠0) 2、下列函数中,哪些是二次函数? y=x ②y=x - ③y=x-x ④y=x + -1 ⑤y=x +2x-4 ③ ⑤ 一次函数的图像是什么? 一条直线 4、通常怎样画一个函数的图像? 描点法:列表、描点、连线 本节课来学习最简单的二次函数的图像 设计意图:巩固上节课学习的二次函数的概念,过度到学它的图像和性质,其中讲到一次函数的图像研究方法,为的是让学生在他们熟悉的知识上引发思考,探究新知。 二)、新授 活动一、画一画 用描点法画的图像 师:画之前思考:x的范围?用几个点画更全面些? 预设学生回答:所有范围正数、0、负数,3个 老师补充:至少5个数,图像更具体更容易观察。 1、列表: x…-3-2-10123…y…9410149…
2、描点 3、连线 老师讲解是用平滑的曲线连接 活动二、看一看 图像有哪些特点? 生:它是一条曲线,开口向上 师补充说明,类似于投篮或是掷铅球时球在空中经过的路线得出:这条曲线叫抛物线,顺便说明二次函数的图像都是开口向上或者向下的抛物线。 生:是轴对称图形 师:关于哪条线对称? 生:y轴 师补充说明,y轴也写成x=0,y轴与抛物线相交于?有何特点? 生:(0,0),在最低位置 师:把这个点叫抛物线的顶点,此时抛物线有最低点。 抛物线的变化趋势如何? 预设学生回答在左侧从左往右下降,在右侧从左往右上升 师引导补充:在a=1即a>0的前提下,左右侧的x、y从左往右分别如何变化? 得出它的变化趋势:a>0,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 活动三、练一练 画y=x 、的图像 三个图像对比有何异同? 1、a>0,开口向上、对称轴是y轴、顶点是原点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大 2、a越大,抛物线的开口越小 活动四、想一想 当a<0时,二次函数的图像和性质? 画、y=x 、的图像 1、一般地,当a<0时,抛物线的开口向下、对称轴是y轴、顶点是原点即抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小 2、a越小,抛物线的开口越小 总的概括:抛物线的对称轴是y轴、顶点是原点, 当a>0时,抛物线的开口向上、顶点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 当a<0时,抛物线的开口向下、顶点是抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小。 |a|越大,抛物线的开口越小。 设计意图:通过画图及观察发现,学生自己总结得出结论,新知更容易理解和消化。类比方法同样的道理,还能对比记忆,整体探究过程体现学生主体性。 三)、巩固练习 书32页:说出抛物线的开口方向、对称轴、顶点 ② ③y=x ④y=x 画 、y=x 的图形
板 书 设 计
二次函数的图像和性质 二次函数的图像是一条抛物线 二次函数的图像性质: 抛物线的对称轴是y轴、顶点是原点 当a>0时,抛物线的开口向上、顶点是抛物线的最低点,当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大。 当a<0时,抛物线的开口向下、顶点是抛物线的最高点、当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小。 |a|越大,抛物线的开口越小。
作 业 分 层 设 计
书41页第三题、第四题 画函数图像: 、 、y=x 写出抛物线 、y=x 的开口方向、对称轴、顶点 选做题: 若A(x1,y1),(x2,y2)在y=x 这条抛物线上,且x1<x2<0,则y1____y2.
教 学 反 思
本节课学习二次函数的图像和性质。导入部分,复习巩固上节课学习的二次函数的概念,过度到学它的图像和性质,其中讲到一次函数的图像研究方法,为的是让学生在他们熟悉的知识上引发思考,探究新知。在新授的过程当中,设计四个活动来进行教学:如何画一画二次函数的(a>0)的图像、看一看此的二次函数的图像有何特点、练一练同学们是否掌握此二次函数的画法、想一想当 a<0时,二次函数的图像和性质?类比讨论,对比出两者的异同,更容易记忆,整体探究过程体现学生主体性。当然过程中的不足是探究的东西多,对于时间上的把控有所欠缺。加上同学们可能在实际画图操作的过程中不是特别熟练,所以新课的内容没办法在现有的时间内完成。
同课章节目录
