人教版2024-2025学年九年级数学上册22.3 实际问题与二次函数 课后同步练习(含答案)
文档属性
| 名称 | 人教版2024-2025学年九年级数学上册22.3 实际问题与二次函数 课后同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 915.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-03 13:37:13 | ||
图片预览




文档简介
人教版2024-2025学年九年级数学上册22.3实际问题与二次函数
课后同步练习
学校:___________ 姓名:___________ 班级:___________
一、单选题
1.如图,福州西湖公园上有一座造型为抛物线形状的拱桥,因其宛如玉带,从而被人称为玉带桥,经测量,玉带桥的拱顶离水面的平均高度为,若玉带桥所在的这条抛物线表示的二次函数为,则该抛物线所在的平面直角坐标系是如下的( )
A.以抛物线的顶点为原点,以抛物线的对称轴为轴
B.以抛物线与水面的左交点为原点,以水面为轴
C.以水面为轴,以抛物线的对称轴为轴
D.以图中夕阳所在位置为原点,以抛物线的对称轴为轴
2.有一块石头从高的绝壁落下,小明查阅相关资料得知物体下落高度与下落时间的关系为,并通过关系式列出下表,则该石头落到海面时t的范围是( )
0 1 2 3 4
0 5 20 45 80
A. B. C. D.
3.某小组同学为了研究太阳照射下物体影长的变化规律,某日在学校操场上竖立一根直杆,经研究发现,当日该直杆的影长与时间的关系近似于二次函数,并在,,这三个时刻,测得该直杆的影长分别约为,,.根据该小组研究结果,下列关于当日该直杆影长的判断正确的是( )
A.前,直杆的影子逐渐变长
B.后,直杆的影子逐渐变长
C.在到之间,还有某个时刻直杆的影长也为
D.在到之间,会有某个时刻直杆的影长达到当日最短
4.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段表示水平的路面,以O为坐标原点所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A. B. C. D.
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度(单位:)与足球被踢出后经过的时间(单位:)之间的关系如下表:
0 1 2 3 4 5 6 7 …
0 8 14 18 20 20 18 14 …
下列结论正确的是( )
A.足球飞行路线的对称轴是直线
B.足球距离地面的最大高度为
C.足球被踢出时落地
D.足球被踢出时,距离地面的高度是
6.“直播带货”已经成为一种热门的销售方式,某直播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).经调查发现每件售价99元时,日销售量为300件,当每件电子产品每下降1元时,日销售量会增加3件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为(元),主播每天的利润为(元),则与之间的函数解析式为( )
A. B.
C. D.
7.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,小敏从奥体中心站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:km),乘坐地铁的时间(单位:s)是关于x的一次函数,若小敏骑单车的时间(单位:s)也受x的影响,其关系可以用来描述,则小敏从文化宫回到家里所需的时间最短为( )
A.34分钟 B.39分钟 C.34.5分钟 D.39.5分钟
8.某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,有下列结论:
①设每件涨价x元,则实际卖出件;
②在降价的情况下,降价5元,即定价55元时,利润最大,最大利润是6250元;
③综合涨价与降价两种情况及现在的销售状况可知,定价元时利润最大;
其中,正确结论的个数是( )
A.0个 B.1个 C.2个 D.3个
9.如图,小明站在原点处,从离地面高度为的点A处抛出弹力球,弹力球在B处着地后弹起,落至点C处,弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,弹力球第一次着地前抛物线的解析式为,弹力球在B处着地后弹起的最大高度为着地前手抛出的最大高度的一半,如果在地上摆放一个底面半径为,高为的圆柱形筐,筐的最左端距离原点为米,若要弹力球从B点弹起后落入筐内,则的值可以是( )
A.7 B.9 C.10 D.8
10.在抛物线上任取一点A(非坐标原点O),连接OA,在OA上取点B,使,则顶点在原点且过点B的抛物线的表达式为( )
A. B. C. D.
二、填空题
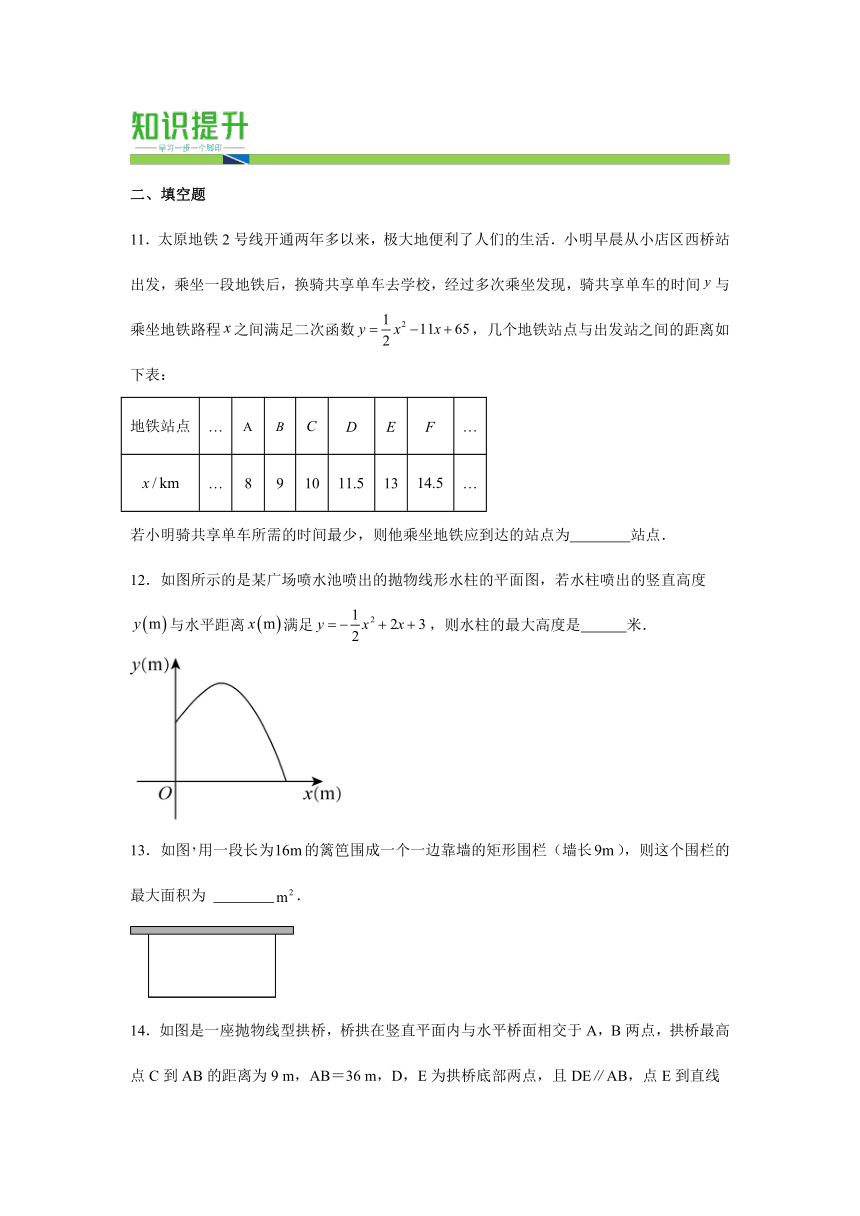
11.太原地铁2号线开通两年多以来,极大地便利了人们的生活.小明早晨从小店区西桥站出发,乘坐一段地铁后,换骑共享单车去学校,经过多次乘坐发现,骑共享单车的时间与乘坐地铁路程之间满足二次函数,几个地铁站点与出发站之间的距离如下表:
地铁站点 … …
… 8 9 10 13 …
若小明骑共享单车所需的时间最少,则他乘坐地铁应到达的站点为 站点.
12.如图所示的是某广场喷水池喷出的抛物线形水柱的平面图,若水柱喷出的竖直高度与水平距离满足,则水柱的最大高度是 米.
13.如图用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),则这个围栏的最大面积为 .
14.如图是一座抛物线型拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,拱桥最高点C到AB的距离为9 m,AB=36 m,D,E为拱桥底部两点,且DE∥AB,点E到直线AB的距离为7 m,则DE长为 m.
15.印刷厂10月份印刷一畅销小说书5万册,因购买此书人数激增,印刷厂需加印,若设印书量每月的增长率为x,12月印书量y万册,写出y关于x的函数解析式 .
三、解答题
16.正方形的边长为4,当边长增加x时,面积增加y,求y与x之间的函数关系式.
17.足球训练中,小辉从球门正前方8米的A处射门,球射向球门的路线呈抛物线.当球离球门的水平距离为2米时,球达到最高点,此时球离地面3米.现以为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)已知球门高为2.44米,通过计算判断球能否射进球门(忽略其他因素).
18.“一人一盔安全守规,一人一带平安常在!”某商店销售一批头盔,售价为每顶60元,每月可卖出300顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月要多卖出20件;已知头盔的进价为每顶40元,求每顶头盔的售价定为多少元时,该商店每月可获得最大利润,最大利润是多少?
19.如图1,抛物线与轴交于、两点(点在点左侧),与轴负半轴交于点,若且.
(1)求该抛物线的函数解析式;
(2)如图1,点在第四象限内的抛物线上且平分,求点的坐标;
(3)如图2,直线与线段交于点,与抛物线交于点,动点在B、G两点之间的抛物线上,直线、与直线分别交于、两点, 若恒为定值,求的值.
20.某数学小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中心考察.
【知识背景】“道路千万条,安全第一条”.汽车刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离y(单位:m)与刹车后行驶时间t(单位:s)之间成二次函数关系,函数图象如图所示.
【问题解决】请根据以上信息,完成下列问题:
(1)求二次函数的解析式(不要求写出自变量的取值范围);
(2)若在汽车前处,有一测速仪,当汽车刹车过程中,经过多少时间,汽车超过测速仪;
(3)若汽车司机发现正前方处有一辆抛锚的车停在路面,立刻刹车,问该车在不变道的情况下是否会撞到抛锚的车?试说明理由.
21.某商城在2024年元旦节期间举行促销活动,一种热销商品进货价为每个14元,标价为每个20元.
(1)商城举行了“感恩老客户”活动,对于老客户,商城连续两次降价,每次降价的百分率相同,最后以每个16.2元的价格售出,求商城每次降价的百分率;
(2)市场调研表明:当每个售价20元时,平均每天能够售出40个,当每个售价每降1元时,平均每天就能多售出10个,在保证每个商品的售价不低于进价的前提下,商城要想获得最大利润,每个商品的定价应为多少元?最大利润是多少?
22.2024年巴黎奥运会8月6日单人10米决赛中,全红婵以425.60分的总分夺得第一获得金牌,陈芋汐位列第二获得银牌.在精彩的比赛过程中,全红婵选择了一个极具难度的(向后翻腾三周半抱膝).如图2所示,建立平面直角坐标系.如果她从点起跳后的运动路线可以看作抛物线的一部分,从起跳到入水的过程中她的竖直高度(单位:米)与水平距离(单位:米)近似满足函数关系式.
水平距离 3 4 4.5
竖直高度 10 11.25 10 6.25
(1)在平时训练完成一次跳水动作时,全红婵的水平距离与竖直高度的几组数据如上:根据上述数据,直接写出的值为______,直接写出满足的函数关系式:______;
(2)比赛当天的某一次跳水中,全红婵的竖直高度与水平距离近似满足函数关系:,记她训练的入水点的水平距离为;比赛当天入水点的水平距离为,则______(填,,);
(3)在(2)的情况下,全红婵起跳后到达最高点开始计时,若点到水平面的距离为,则她到水面的距离与时间之间近似满足,如果全红婵在达到最高点后需要1.4秒的时间才能完成极具难度的动作,请通过计算说明,她当天的比赛能否成功完成此动作?
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D A C D B D D
11.D
12.5
13.
14.48
15.
16.
17.(1)
(2)球不能射进球门
18.每顶头盔的售价定为57.5元时,利润最大,最大利润为6125元.
19.(1)
(2)
(3)
20.(1)
(2)汽车刹车后,汽车与测速仪相距
(3)不会,理由见解析
21.(1)
(2)19元;250元
答:定价为19元,最大利润为250元.
22.(1),;
(2)
(3)她当天的比赛能成功完成此动作.
课后同步练习
学校:___________ 姓名:___________ 班级:___________
一、单选题
1.如图,福州西湖公园上有一座造型为抛物线形状的拱桥,因其宛如玉带,从而被人称为玉带桥,经测量,玉带桥的拱顶离水面的平均高度为,若玉带桥所在的这条抛物线表示的二次函数为,则该抛物线所在的平面直角坐标系是如下的( )
A.以抛物线的顶点为原点,以抛物线的对称轴为轴
B.以抛物线与水面的左交点为原点,以水面为轴
C.以水面为轴,以抛物线的对称轴为轴
D.以图中夕阳所在位置为原点,以抛物线的对称轴为轴
2.有一块石头从高的绝壁落下,小明查阅相关资料得知物体下落高度与下落时间的关系为,并通过关系式列出下表,则该石头落到海面时t的范围是( )
0 1 2 3 4
0 5 20 45 80
A. B. C. D.
3.某小组同学为了研究太阳照射下物体影长的变化规律,某日在学校操场上竖立一根直杆,经研究发现,当日该直杆的影长与时间的关系近似于二次函数,并在,,这三个时刻,测得该直杆的影长分别约为,,.根据该小组研究结果,下列关于当日该直杆影长的判断正确的是( )
A.前,直杆的影子逐渐变长
B.后,直杆的影子逐渐变长
C.在到之间,还有某个时刻直杆的影长也为
D.在到之间,会有某个时刻直杆的影长达到当日最短
4.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段表示水平的路面,以O为坐标原点所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A. B. C. D.
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度(单位:)与足球被踢出后经过的时间(单位:)之间的关系如下表:
0 1 2 3 4 5 6 7 …
0 8 14 18 20 20 18 14 …
下列结论正确的是( )
A.足球飞行路线的对称轴是直线
B.足球距离地面的最大高度为
C.足球被踢出时落地
D.足球被踢出时,距离地面的高度是
6.“直播带货”已经成为一种热门的销售方式,某直播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).经调查发现每件售价99元时,日销售量为300件,当每件电子产品每下降1元时,日销售量会增加3件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为(元),主播每天的利润为(元),则与之间的函数解析式为( )
A. B.
C. D.
7.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,小敏从奥体中心站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:km),乘坐地铁的时间(单位:s)是关于x的一次函数,若小敏骑单车的时间(单位:s)也受x的影响,其关系可以用来描述,则小敏从文化宫回到家里所需的时间最短为( )
A.34分钟 B.39分钟 C.34.5分钟 D.39.5分钟
8.某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,有下列结论:
①设每件涨价x元,则实际卖出件;
②在降价的情况下,降价5元,即定价55元时,利润最大,最大利润是6250元;
③综合涨价与降价两种情况及现在的销售状况可知,定价元时利润最大;
其中,正确结论的个数是( )
A.0个 B.1个 C.2个 D.3个
9.如图,小明站在原点处,从离地面高度为的点A处抛出弹力球,弹力球在B处着地后弹起,落至点C处,弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,弹力球第一次着地前抛物线的解析式为,弹力球在B处着地后弹起的最大高度为着地前手抛出的最大高度的一半,如果在地上摆放一个底面半径为,高为的圆柱形筐,筐的最左端距离原点为米,若要弹力球从B点弹起后落入筐内,则的值可以是( )
A.7 B.9 C.10 D.8
10.在抛物线上任取一点A(非坐标原点O),连接OA,在OA上取点B,使,则顶点在原点且过点B的抛物线的表达式为( )
A. B. C. D.
二、填空题
11.太原地铁2号线开通两年多以来,极大地便利了人们的生活.小明早晨从小店区西桥站出发,乘坐一段地铁后,换骑共享单车去学校,经过多次乘坐发现,骑共享单车的时间与乘坐地铁路程之间满足二次函数,几个地铁站点与出发站之间的距离如下表:
地铁站点 … …
… 8 9 10 13 …
若小明骑共享单车所需的时间最少,则他乘坐地铁应到达的站点为 站点.
12.如图所示的是某广场喷水池喷出的抛物线形水柱的平面图,若水柱喷出的竖直高度与水平距离满足,则水柱的最大高度是 米.
13.如图用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),则这个围栏的最大面积为 .
14.如图是一座抛物线型拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,拱桥最高点C到AB的距离为9 m,AB=36 m,D,E为拱桥底部两点,且DE∥AB,点E到直线AB的距离为7 m,则DE长为 m.
15.印刷厂10月份印刷一畅销小说书5万册,因购买此书人数激增,印刷厂需加印,若设印书量每月的增长率为x,12月印书量y万册,写出y关于x的函数解析式 .
三、解答题
16.正方形的边长为4,当边长增加x时,面积增加y,求y与x之间的函数关系式.
17.足球训练中,小辉从球门正前方8米的A处射门,球射向球门的路线呈抛物线.当球离球门的水平距离为2米时,球达到最高点,此时球离地面3米.现以为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)已知球门高为2.44米,通过计算判断球能否射进球门(忽略其他因素).
18.“一人一盔安全守规,一人一带平安常在!”某商店销售一批头盔,售价为每顶60元,每月可卖出300顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月要多卖出20件;已知头盔的进价为每顶40元,求每顶头盔的售价定为多少元时,该商店每月可获得最大利润,最大利润是多少?
19.如图1,抛物线与轴交于、两点(点在点左侧),与轴负半轴交于点,若且.
(1)求该抛物线的函数解析式;
(2)如图1,点在第四象限内的抛物线上且平分,求点的坐标;
(3)如图2,直线与线段交于点,与抛物线交于点,动点在B、G两点之间的抛物线上,直线、与直线分别交于、两点, 若恒为定值,求的值.
20.某数学小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中心考察.
【知识背景】“道路千万条,安全第一条”.汽车刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离y(单位:m)与刹车后行驶时间t(单位:s)之间成二次函数关系,函数图象如图所示.
【问题解决】请根据以上信息,完成下列问题:
(1)求二次函数的解析式(不要求写出自变量的取值范围);
(2)若在汽车前处,有一测速仪,当汽车刹车过程中,经过多少时间,汽车超过测速仪;
(3)若汽车司机发现正前方处有一辆抛锚的车停在路面,立刻刹车,问该车在不变道的情况下是否会撞到抛锚的车?试说明理由.
21.某商城在2024年元旦节期间举行促销活动,一种热销商品进货价为每个14元,标价为每个20元.
(1)商城举行了“感恩老客户”活动,对于老客户,商城连续两次降价,每次降价的百分率相同,最后以每个16.2元的价格售出,求商城每次降价的百分率;
(2)市场调研表明:当每个售价20元时,平均每天能够售出40个,当每个售价每降1元时,平均每天就能多售出10个,在保证每个商品的售价不低于进价的前提下,商城要想获得最大利润,每个商品的定价应为多少元?最大利润是多少?
22.2024年巴黎奥运会8月6日单人10米决赛中,全红婵以425.60分的总分夺得第一获得金牌,陈芋汐位列第二获得银牌.在精彩的比赛过程中,全红婵选择了一个极具难度的(向后翻腾三周半抱膝).如图2所示,建立平面直角坐标系.如果她从点起跳后的运动路线可以看作抛物线的一部分,从起跳到入水的过程中她的竖直高度(单位:米)与水平距离(单位:米)近似满足函数关系式.
水平距离 3 4 4.5
竖直高度 10 11.25 10 6.25
(1)在平时训练完成一次跳水动作时,全红婵的水平距离与竖直高度的几组数据如上:根据上述数据,直接写出的值为______,直接写出满足的函数关系式:______;
(2)比赛当天的某一次跳水中,全红婵的竖直高度与水平距离近似满足函数关系:,记她训练的入水点的水平距离为;比赛当天入水点的水平距离为,则______(填,,);
(3)在(2)的情况下,全红婵起跳后到达最高点开始计时,若点到水平面的距离为,则她到水面的距离与时间之间近似满足,如果全红婵在达到最高点后需要1.4秒的时间才能完成极具难度的动作,请通过计算说明,她当天的比赛能否成功完成此动作?
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D A C D B D D
11.D
12.5
13.
14.48
15.
16.
17.(1)
(2)球不能射进球门
18.每顶头盔的售价定为57.5元时,利润最大,最大利润为6125元.
19.(1)
(2)
(3)
20.(1)
(2)汽车刹车后,汽车与测速仪相距
(3)不会,理由见解析
21.(1)
(2)19元;250元
答:定价为19元,最大利润为250元.
22.(1),;
(2)
(3)她当天的比赛能成功完成此动作.
同课章节目录
