不等关系(北师大教材必修五)
图片预览



文档简介
课件9张PPT。3.1不等关系与不等式3.1.2比较大小自学探究1)不等式的两边同时加上或减去同一个数,不等号的方向不改变,即
2)不等式的两边同时乘以或除以同一个正数,不等号的方向不改变,即
3)不等式的两边同时乘以或除以同一个负数,不等号的方向改变,即不等式的性质若a>b,则a±c>b±c复习若a>b且c>0,则ac>bc若a>b且c<0,则ac=( )-( )
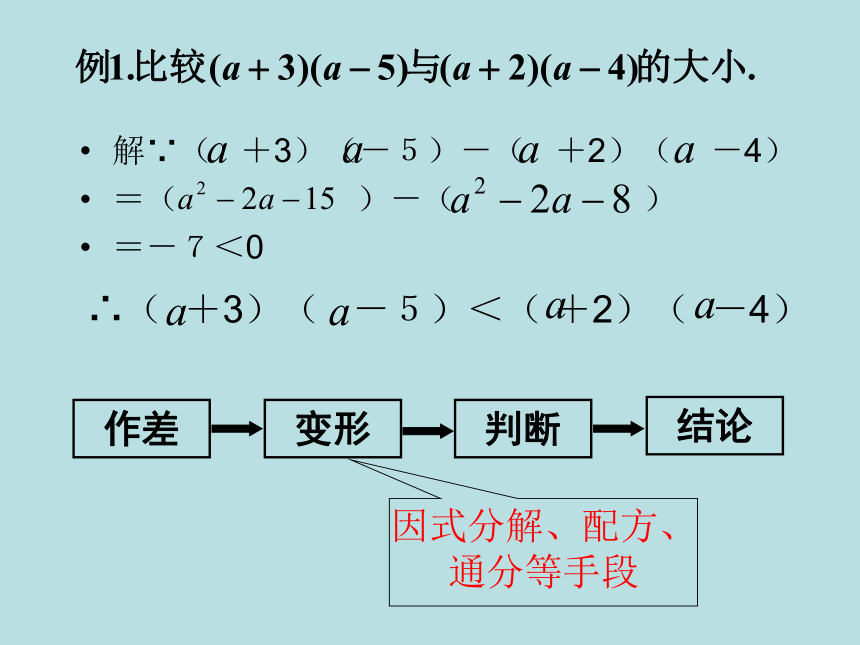
=-7<0∴( +3)( -5)<( +2)( -4)作差变形判断因式分解、配方、通分等手段结论例2.已知1≤a-b ≤2,2 ≤a+b ≤4,求5a-b的范围.
解:令5a-b=x(a-b)+(a+b)
5a-b=(x+y)+(-x+y)b
∴x+y=5且-x+y=-1得x=3,y=2
由3 ≤3(a-b) ≤6, ①4 ≤2(a+b) ≤8②
①+ ②得7 ≤ 5a-b ≤14.例3、建筑设计规定,民用住宅的窗户面积必须小于地板面积。但按采光标准,窗户面积与地板面积的比值应不小于10%,且这个比值越大, 住宅的采光条件越好.试问:同时增加相等的窗户面积和地板面积, 住宅的采光条件是变好了,还是变坏了?解:设住宅的窗户面积和地板面积分别为a,b,同时增加的面积为m,根据问题的要求a< b,且 ≥10%由于 >0于是 >又≥10%,-- 因此 >≥10% 所以, 同时增加相等的窗户面积和地板面积后,住宅的采光条件变好了!=一般地, 设a,b为正实数,且a< b,m>0,则有 >思考:1.甲,乙两人同时从A地出发沿同一路线走到B地,所用时间分别为t1、t2,甲有一半时间以速度m行走,另一半时间以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走,且,m≠n. (1)请你与同学各算出t1与t2 (用m,n表示); (2)与同学一起比较与t1、t2 的大小,并判断甲,乙谁先到达B地.2.老古炒股票,第一天涨了10%,第二天跌了10%,问:老古炒股票是赚了还是亏了?.课时小结 本节课复习了不等式的性质,研究了如何比较两个实数(代数式)的大小——作差法,其具体解题步骤可归纳为: 第一步:作差并化简,其目标应是n个因式之积或完全平方式或常数的形式; 第二步:判断差值与零的大小关系,必要时须进行讨论; 第三步:得出结论 作业: 课本P74习题3.1[A组]第3题[B组] 第3题
2)不等式的两边同时乘以或除以同一个正数,不等号的方向不改变,即
3)不等式的两边同时乘以或除以同一个负数,不等号的方向改变,即不等式的性质若a>b,则a±c>b±c复习若a>b且c>0,则ac>bc若a>b且c<0,则ac
=-7<0∴( +3)( -5)<( +2)( -4)作差变形判断因式分解、配方、通分等手段结论例2.已知1≤a-b ≤2,2 ≤a+b ≤4,求5a-b的范围.
解:令5a-b=x(a-b)+(a+b)
5a-b=(x+y)+(-x+y)b
∴x+y=5且-x+y=-1得x=3,y=2
由3 ≤3(a-b) ≤6, ①4 ≤2(a+b) ≤8②
①+ ②得7 ≤ 5a-b ≤14.例3、建筑设计规定,民用住宅的窗户面积必须小于地板面积。但按采光标准,窗户面积与地板面积的比值应不小于10%,且这个比值越大, 住宅的采光条件越好.试问:同时增加相等的窗户面积和地板面积, 住宅的采光条件是变好了,还是变坏了?解:设住宅的窗户面积和地板面积分别为a,b,同时增加的面积为m,根据问题的要求a< b,且 ≥10%由于 >0于是 >又≥10%,-- 因此 >≥10% 所以, 同时增加相等的窗户面积和地板面积后,住宅的采光条件变好了!=一般地, 设a,b为正实数,且a< b,m>0,则有 >思考:1.甲,乙两人同时从A地出发沿同一路线走到B地,所用时间分别为t1、t2,甲有一半时间以速度m行走,另一半时间以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走,且,m≠n. (1)请你与同学各算出t1与t2 (用m,n表示); (2)与同学一起比较与t1、t2 的大小,并判断甲,乙谁先到达B地.2.老古炒股票,第一天涨了10%,第二天跌了10%,问:老古炒股票是赚了还是亏了?.课时小结 本节课复习了不等式的性质,研究了如何比较两个实数(代数式)的大小——作差法,其具体解题步骤可归纳为: 第一步:作差并化简,其目标应是n个因式之积或完全平方式或常数的形式; 第二步:判断差值与零的大小关系,必要时须进行讨论; 第三步:得出结论 作业: 课本P74习题3.1[A组]第3题[B组] 第3题
