初中数学人教版八年级上册 第十二章 全等三角形单元测试(含答案)
文档属性
| 名称 | 初中数学人教版八年级上册 第十二章 全等三角形单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-03 20:18:40 | ||
图片预览




文档简介
第十二章 全等三角形
一、选择题
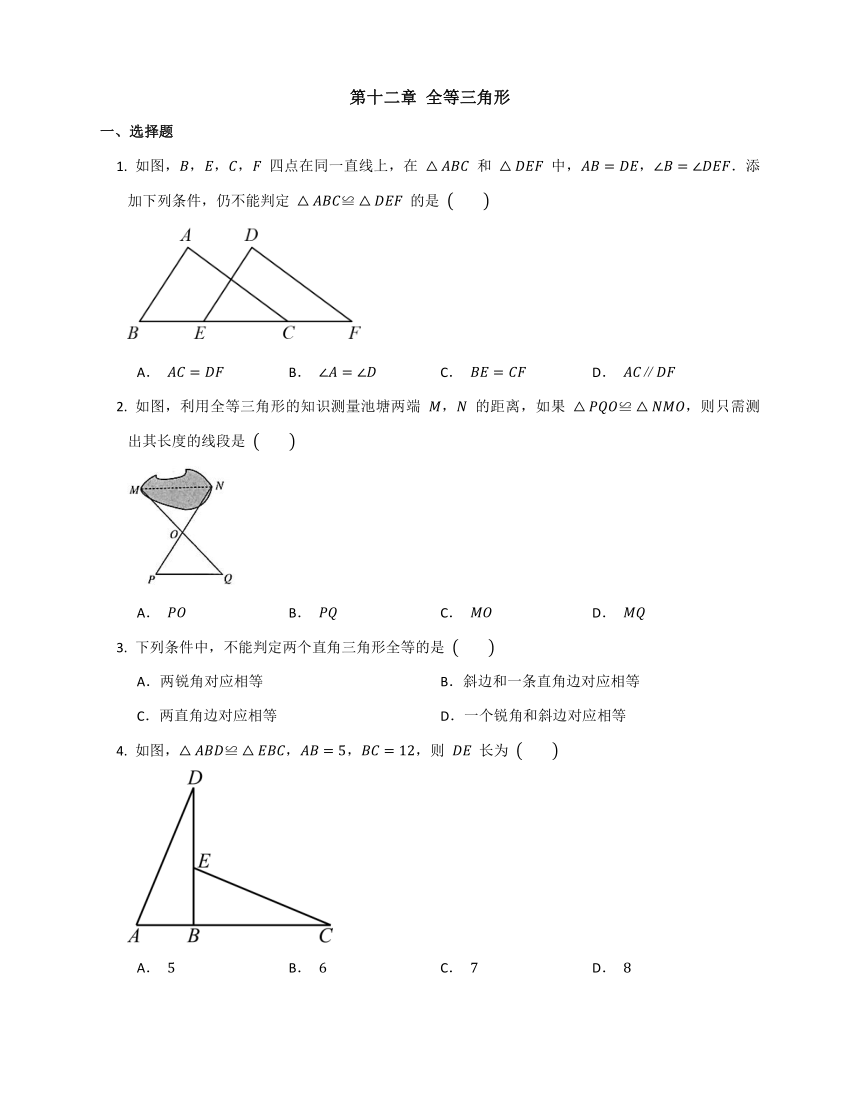
如图,,,, 四点在同一直线上,在 和 中,,.添加下列条件,仍不能判定 的是
A. B. C. D.
如图,利用全等三角形的知识测量池塘两端 , 的距离,如果 ,则只需测出其长度的线段是
A. B. C. D.
下列条件中,不能判定两个直角三角形全等的是
A.两锐角对应相等 B.斜边和一条直角边对应相等
C.两直角边对应相等 D.一个锐角和斜边对应相等
如图,,,,则 长为
A. B. C. D.
如图,,, 相交于点 ,且它们被点 平分,则图中共有全等三角形
A. 对 B. 对 C. 对 D. 对
如图,在方格纸中,以 为一边作 ,使之与 全等,从 ,,, 四个点中找出符合条件的点 ,则点 有
A. 个 B. 个 C. 个 D. 个
如图,在 中,, 平分 交 于点 ,若 ,点 到 的距离为 ,则 的长为
A. B. C. D.
如图,在 和 中,,, 与 相交于点 ,与 相交于点 , 与 相交于点 ,.有下列结论:
① ;
② ;
③ ;
④ .
其中正确结论的个数是
A. 个 B. 个 C. 个 D. 个
二、填空题
如图,已知 ,,,则 .
如图,小敏做了一个角平分仪 ,其中 ,,将仪器上的点 与 的顶点 重合,调整 和 ,使它们分别落在角的两边上,过点 , 画一条射线 , 就是 的平分线.此角平分仪的画图原理是:根据仪器结构,可得 ,这样就有 .则说明这两个三角形全等的依据是 .
如图, 中,,, 为 延长线上一点,点 在 上,且 ,若 ,则 度.
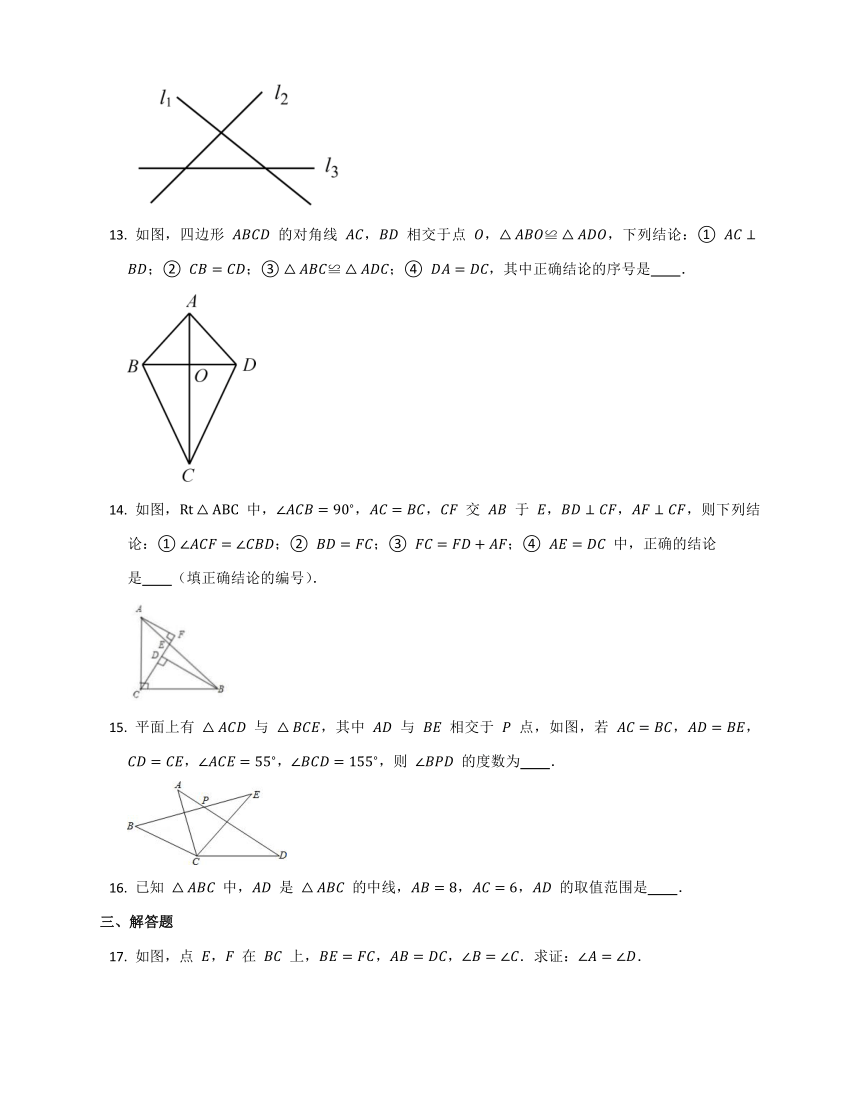
如图,直线 ,, 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 处.
如图,四边形 的对角线 , 相交于点 ,,下列结论:① ;② ;③ ;④ ,其中正确结论的序号是 .
如图, 中,,, 交 于 ,,,则下列结论:① ;② ;③ ;④ 中,正确的结论
是 (填正确结论的编号).
平面上有 与 ,其中 与 相交于 点,如图,若 ,,,,,则 的度数为 .
已知 中, 是 的中线,,, 的取值范围是 .
三、解答题
如图,点 , 在 上,,,.求证:.
如图,,.
(1) 请找出图中一对全等的三角形,并说明理由;
(2) 若 ,,求 的度数.
王强同学用 块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点 在 上,点 和 分别与木墙的顶端重合.
(1) 与 全等吗?为什么?
(2) 求两堵木墙之间的距离.
如图,在 中,, 的角平分线 , 相交于点 ,过 点作 交 的延长线于点 ,交 于点 .
(1) 求 的度数.
(2) 求证:.
(3) 求证:.
如图, 于 , 于 ,若 ,.
(1) 求证: 平分 .
(2) 写出 与 之间的等量关系,并说明理由.
答案
一、选择题
1. A
2. B
3. A
4. C
5. C
6. C
7. A
8. C
二、填空题
9.
10.
11.
12.
13. ①②③
14. ①②③
15.
16.
三、解答题
17. ,
,
即 ,
在 和 中,
,
.
18.
(1) .
理由:在 与 中,
,
.
(2) 由( )可知:,
,
,
,
,
在 中,,
19.
(1) 由题意可知,,,
又 ,
,
,
,
在 与 中,
.
(2) 由题意可知:,,
,
,,
.
答:两堵木墙之间的距离为 .
20.
(1) 的角平分线为 ,,
,,
.
(2) ,
,
,
在 和 中,
.
(3) ,
,,
又 ,且 ,
,
在 和 中,
,
,
.
21.
(1) 在 与 中,.
.
,即 平分 .
(2) .
理由:
, 平分 ,
,
,
,
在 与 中,
,
,
.
一、选择题
如图,,,, 四点在同一直线上,在 和 中,,.添加下列条件,仍不能判定 的是
A. B. C. D.
如图,利用全等三角形的知识测量池塘两端 , 的距离,如果 ,则只需测出其长度的线段是
A. B. C. D.
下列条件中,不能判定两个直角三角形全等的是
A.两锐角对应相等 B.斜边和一条直角边对应相等
C.两直角边对应相等 D.一个锐角和斜边对应相等
如图,,,,则 长为
A. B. C. D.
如图,,, 相交于点 ,且它们被点 平分,则图中共有全等三角形
A. 对 B. 对 C. 对 D. 对
如图,在方格纸中,以 为一边作 ,使之与 全等,从 ,,, 四个点中找出符合条件的点 ,则点 有
A. 个 B. 个 C. 个 D. 个
如图,在 中,, 平分 交 于点 ,若 ,点 到 的距离为 ,则 的长为
A. B. C. D.
如图,在 和 中,,, 与 相交于点 ,与 相交于点 , 与 相交于点 ,.有下列结论:
① ;
② ;
③ ;
④ .
其中正确结论的个数是
A. 个 B. 个 C. 个 D. 个
二、填空题
如图,已知 ,,,则 .
如图,小敏做了一个角平分仪 ,其中 ,,将仪器上的点 与 的顶点 重合,调整 和 ,使它们分别落在角的两边上,过点 , 画一条射线 , 就是 的平分线.此角平分仪的画图原理是:根据仪器结构,可得 ,这样就有 .则说明这两个三角形全等的依据是 .
如图, 中,,, 为 延长线上一点,点 在 上,且 ,若 ,则 度.
如图,直线 ,, 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 处.
如图,四边形 的对角线 , 相交于点 ,,下列结论:① ;② ;③ ;④ ,其中正确结论的序号是 .
如图, 中,,, 交 于 ,,,则下列结论:① ;② ;③ ;④ 中,正确的结论
是 (填正确结论的编号).
平面上有 与 ,其中 与 相交于 点,如图,若 ,,,,,则 的度数为 .
已知 中, 是 的中线,,, 的取值范围是 .
三、解答题
如图,点 , 在 上,,,.求证:.
如图,,.
(1) 请找出图中一对全等的三角形,并说明理由;
(2) 若 ,,求 的度数.
王强同学用 块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点 在 上,点 和 分别与木墙的顶端重合.
(1) 与 全等吗?为什么?
(2) 求两堵木墙之间的距离.
如图,在 中,, 的角平分线 , 相交于点 ,过 点作 交 的延长线于点 ,交 于点 .
(1) 求 的度数.
(2) 求证:.
(3) 求证:.
如图, 于 , 于 ,若 ,.
(1) 求证: 平分 .
(2) 写出 与 之间的等量关系,并说明理由.
答案
一、选择题
1. A
2. B
3. A
4. C
5. C
6. C
7. A
8. C
二、填空题
9.
10.
11.
12.
13. ①②③
14. ①②③
15.
16.
三、解答题
17. ,
,
即 ,
在 和 中,
,
.
18.
(1) .
理由:在 与 中,
,
.
(2) 由( )可知:,
,
,
,
,
在 中,,
19.
(1) 由题意可知,,,
又 ,
,
,
,
在 与 中,
.
(2) 由题意可知:,,
,
,,
.
答:两堵木墙之间的距离为 .
20.
(1) 的角平分线为 ,,
,,
.
(2) ,
,
,
在 和 中,
.
(3) ,
,,
又 ,且 ,
,
在 和 中,
,
,
.
21.
(1) 在 与 中,.
.
,即 平分 .
(2) .
理由:
, 平分 ,
,
,
,
在 与 中,
,
,
.
