人教版数学八年级上册(新)课件:12.2探索三角形全等的条件(共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册(新)课件:12.2探索三角形全等的条件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 697.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-13 18:37:34 | ||
图片预览



文档简介
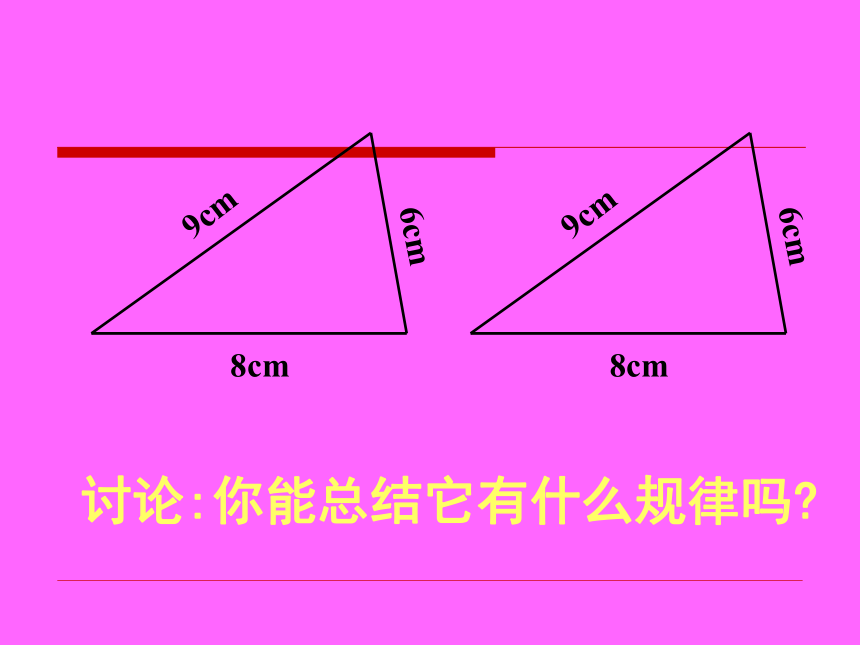
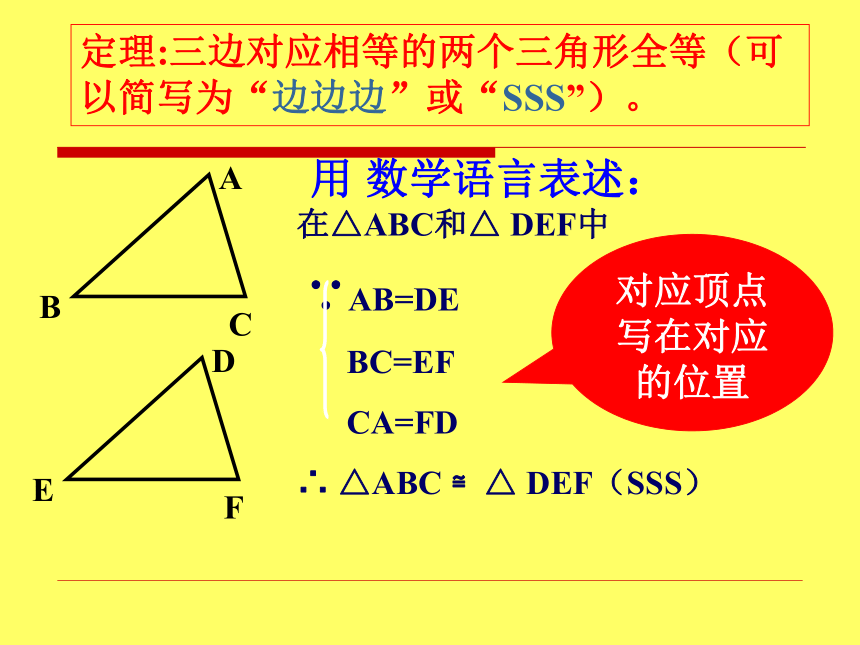
课件14张PPT。探索三角形全等的条件回顾与思考 到目前为止,我们已学过哪些方法判定两个三角形全等?答:边边边(SAS)、角边角(ASA)角角边(AAS) 根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?答:三边相等讨论:你能总结它有什么规律吗?定理:三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。对应顶点写在对应的位置用 数学语言表述:三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性。思考:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了.你能用“边边边”解释这个事例吗?例1:如图, △ABC是一个钢架,
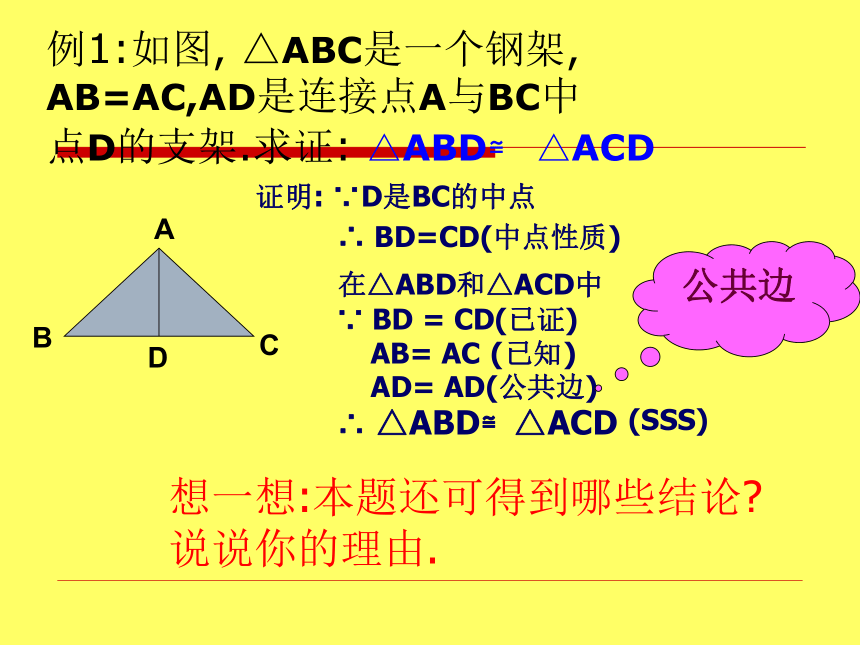
AB=AC,AD是连接点A与BC中
点D的支架.求证: △ABD≌ △ACD在△ABD和△ACD中∵ BD = CD(已证)AB= AC (已知)∴ △ABD≌△ACD(SSS)证明: ∵D是BC的中点∴ BD=CD(中点性质)AD= AD(公共边)想一想:本题还可得到哪些结论?说说你的理由.公共边议一议:
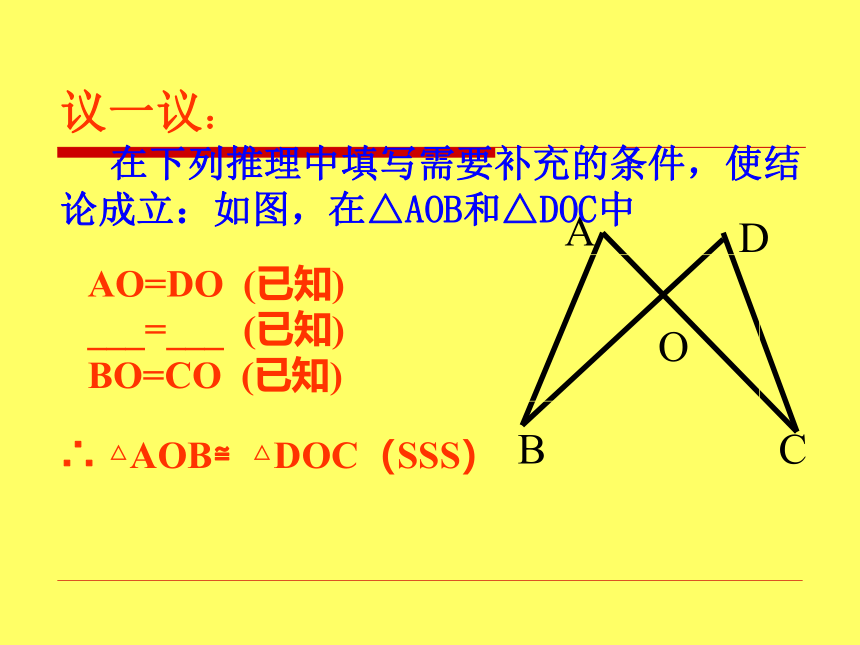
在下列推理中填写需要补充的条件,使结论成立:如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,还应该有AB=FD这个条件∵ DB是AB与FD的公共部分,且AD=FB
∴ AD+DB=FB+DB
即 AB=FD解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS 想一想△ABC ≌ ( ) 1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 △DCBBCCBBF=CD或 BD=CF1、今天我们学习哪种方法判定两三角形全等?答:边角边(SSS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、ASA、AAS3、在这四种说明三角形全等的条件中,你发现了什么?答:至少有一个条件:边相等“边边角”不能判定两个三角形全等作业1、P82页习题3.4A 第8、9题
2、阅读P80—82页 再见祝同学们学习进步已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中∵ AC = A D (已知)
BC = BD (已知)
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)备用题
如图:AB=AD,AE=AF,BE=DF,问:∠BAF与∠DAE相等吗?请说明理由。
在下列推理中填写需要补充的条件,使结论成立:如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,还应该有AB=FD这个条件∵ DB是AB与FD的公共部分,且AD=FB
∴ AD+DB=FB+DB
即 AB=FD解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS 想一想△ABC ≌ ( ) 1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 △DCBBCCBBF=CD或 BD=CF1、今天我们学习哪种方法判定两三角形全等?答:边角边(SSS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、ASA、AAS3、在这四种说明三角形全等的条件中,你发现了什么?答:至少有一个条件:边相等“边边角”不能判定两个三角形全等作业1、P82页习题3.4A 第8、9题
2、阅读P80—82页 再见祝同学们学习进步已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中∵ AC = A D (已知)
BC = BD (已知)
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)备用题
如图:AB=AD,AE=AF,BE=DF,问:∠BAF与∠DAE相等吗?请说明理由。
