第十一章 三角形 单元测试 人教版八年级数学上册(含解析)
文档属性
| 名称 | 第十一章 三角形 单元测试 人教版八年级数学上册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-04 08:34:17 | ||
图片预览



文档简介
人教版八年级数学上册
第十一章三角形
一、选择题
1.以下列各组线段为边,能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
2.已知一个多边形的内角和是外角和的倍,则这个多边形是( )
A. 八边形 B. 九边形 C. 十边形 D. 十二边形
3.若正多边形的内角和是,则该正多边形的一个外角为( )
A. B. C. D.
4.如图,等于( )
A. B. C. D.
5.如图,在中,是边上的高,平分交边于,,,则的大小是( )
A.
B.
C.
D.
6.将一副三角尺按如图摆放,点在上,点在的延长线上,,,,,则的度数是( )
A. B. C. D.
7.如图,,直线平移后得到直线,则( )
A. B. C. D.
8.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则图中的度数为( )
A.
B.
C.
D.
9.如图,是边的中线,、分别是、的中点,若的面积为,则的面积等于( )
A.
B.
C.
D.
10.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
二、填空题
11.三角形的三边长分别为,,,则的取值范围是 .
12.一个边形的内角和是它外角和的倍,则边数______.
13.小明发现交通指示牌中“停车让行标志”可以看成是正八边形,如图所示,则______
14.在中,若,则是_____________三角形.
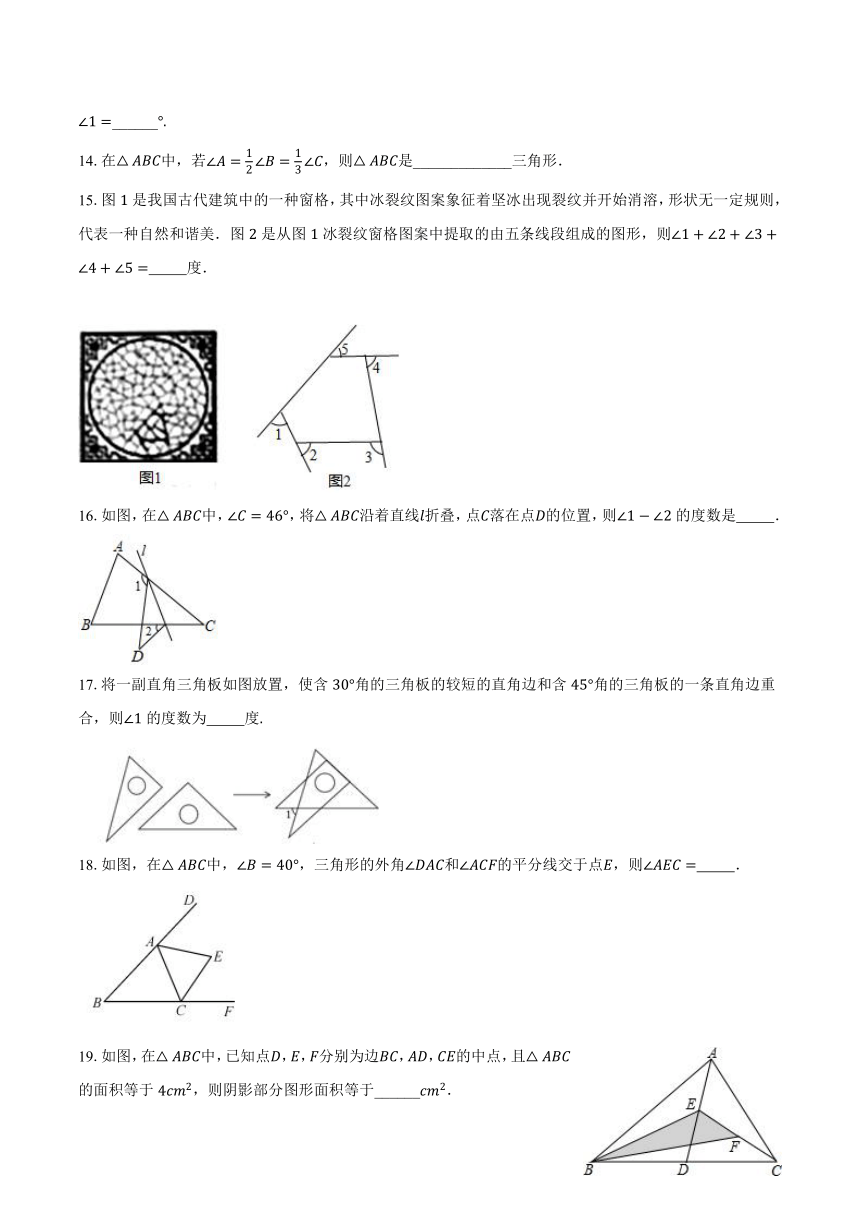
15.图是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图是从图冰裂纹窗格图案中提取的由五条线段组成的图形,则 度.
16.如图,在中,,将沿着直线折叠,点落在点的位置,则的度数是 .
17.将一副直角三角板如图放置,使含角的三角板的较短的直角边和含角的三角板的一条直角边重合,则的度数为 度
18.如图,在中,,三角形的外角和的平分线交于点,则 .
19.如图,在中,已知点,,分别为边,,的中点,且的面积等于,则阴影部分图形面积等于______.
20.如图,已知,,,,,则 度.
三、解答题
21.如图,在中,,,的外角的平分线交的延长线于点.
求的度数;
过点作,交的延长线于点,求的度数.
22.已知:如图,是任意一个三角形,求证:.
23.如图,已知于点,且,,求的度数.
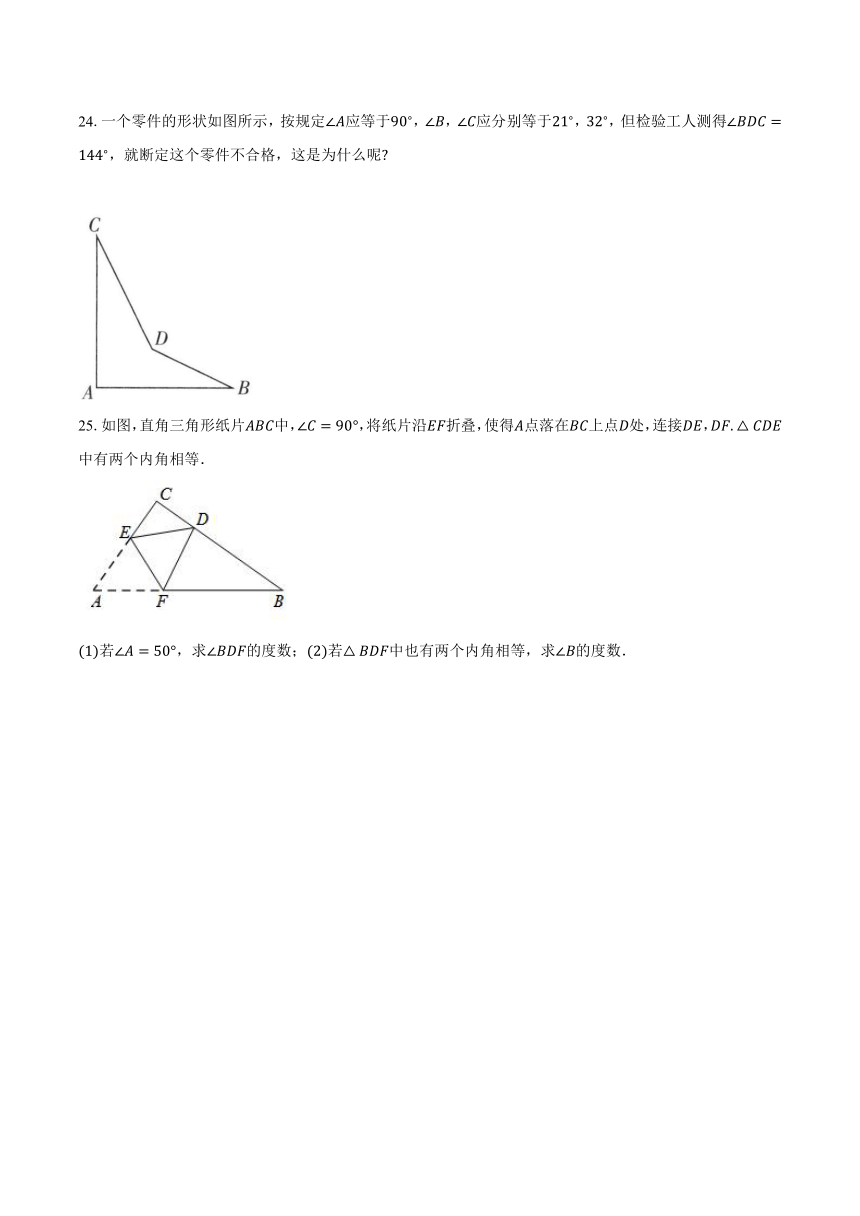
24.一个零件的形状如图所示,按规定应等于,,应分别等于,,但检验工人测得,就断定这个零件不合格,这是为什么呢
25.如图,直角三角形纸片中,,将纸片沿折叠,使得点落在上点处,连接,中有两个内角相等.
若,求的度数;若中也有两个内角相等,求的度数.
答案和解析
1.【答案】
【解析】【分析】
根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
【解答】
解:根据三角形的三边关系,知:
A、,不能组成三角形;
B、,不能组成三角形;
C、,不能组成三角形;
D、,能够组成三角形.
故选:.
2.【答案】
【解析】解:设这个多边形的边数为,则该多边形的内角和为,
依题意得,
解得,
这个多边形的边数是.
故选:.
先设这个多边形的边数为,得出该多边形的内角和为,根据多边形的内角和是外角和的倍,列方程求解.
本题主要考查了多边形内角和定理与外角和定理,多边形内角和且为整数,而多边形的外角和指每个顶点处取一个外角,则边形取个外角,无论边数是几,其外角和始终为.
3.【答案】
【解析】【分析】
本题主要考查了多边形的内角和与外角和之间的关系,关键是记住内角和的公式与外角和的特征,难度适中.
根据多边形的内角和公式求出多边形的边数,再根据多边形的外角和是固定的,依此可以求出多边形的一个外角.
【解答】
解:正多边形的内角和是,
多边形的边数为,
多边形的外角和都是,
多边形的每个外角.
故选:.
4.【答案】
【解析】【分析】
本题考查的是三角形外角的性质及三角形内角和定理,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.
先根据三角形外角的性质得出及的度数,再由三角形内角和定理即可得出结论.
【解答】
解:如图,
是的外角,
;
是的外角,
,
,
.
故选D.
5.【答案】
【解析】【分析】
本题考查了三角形的内角和定理,角平分线的定义,准确识图理清图中各角度之间的关系是解题的关键.
根据角平分线的定义可得,再根据直角三角形两锐角互余求出,然后根据计算即可得解.
【解答】
解:平分,
,
是边上的高,
,
.
故选B.
6.【答案】
【解析】【分析】
本题考查了三角形的内角和定理,平行线的性质,以及三角形的外角性质,牢记“两直线平行,内错角相等”是解题的关键.
根据三角形的内角和定理,得,,根据可得,根据三角形的外角性质得,进而可得答案.
【解答】
解:,,
.
,,
.
,
,
,
.
故选A.
7.【答案】
【解析】【分析】
此题考查了平移的性质,平行线的性质,以及三角形外角的性质,熟练掌握平移的性质是解本题的关键.
由平移的性质得到与平行,利用两直线平行同旁内角互补以及三角形外角性质,即可求出所求.
【解答】
解:如图,
直线平移后得到直线,
,
,
,
,
,,
.
故选C.
8.【答案】
【解析】解:,
,
,
又,
,
故选:。
由邻补角概念和翻折变换性质得出,据此知,结合知,从而得出答案。
本题主要考查翻折变换的性质,解题的关键是掌握翻折变换的对应边、对应角相等的性质及直角三角形两锐角互余、对顶角相等的性质。
9.【答案】
【解析】【分析】
本题考查了三角形的面积公式,掌握三角形的中线把三角形的面积分成相等的两部分是解题的关键.
由于是的中点,,那么和可看作等底同高的两个三角形,根据三角形的面积公式,得出和的面积相等,进而得出的面积等于的面积的倍;同理,由于是的中点,得出的面积等于面积的倍;由于是边上的中线,得出的面积等于面积的倍,代入求解即可.
【解答】
解:是的中点,
,
,
又,
.
同理,.
10.【答案】
【解析】【解答】
解:是中的平分线,是的外角的平分线,
,,
,,
,
,
,
,
,
,
故选:.
【分析】
根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出的度数,根据补角的定义求出的度数,根据三角形的内角和即可求出的度数,即可求出结果.
本题考查了角平分线的定义,一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为,难度适中.
11.【答案】
【解析】【分析】
此题主要考查了三角形的三边关系,属于基础题.
根据三角形的三边关系,可得,再解即可.
【解答】
解:根据三角形的三边关系可得:,
解得:.
故答案为.
12.【答案】
【解析】【分析】
本题主要考查了多边形的内角和的计算公式以及多边形的外角和定理,比较简单.
利用多边形的外角和是,一个边形的内角和等于它外角和的倍,则内角和是,而边形的内角和是,则可得到方程,解之即可.
【解答】
解:设多边形的边数为,
根据题意列方程,得:
,
解得:,
故答案为.
13.【答案】
【解析】解:“停车让行标志”可以看成是正八边形,
;
故答案为:.
根据多边形的外角和是,个外角都相等,即可求出.
此题考查了多边形内角与外角,熟练掌握多边形的外角和是是解题的关键.
14.【答案】直角
【解析】【分析】
本题考查了三角形的内角和定理及直角三角形的判定先设,则,,再根据三角形内角和定理列方程,解方程求出三个角的度数即可判断.
【解答】
解:,
设,则,,
,
,
解得,
,,,
是直角三角形.
故答案为直角.
15.【答案】
【解析】【分析】
本题考查的是多边形的外角和,掌握多边形的外角和等于是解题的关键.
根据多边形的外角和等于解答即可.
【解答】
解:由多边形的外角和等于可知,
.
16.【答案】
【解析】【分析】
此题考查了翻折变换折叠问题以及三角形外角性质,熟练掌握折叠的性质是解本题的关键.
由折叠的性质得到,再利用外角性质即可求出所求角的度数.
【解答】
解:
由折叠的性质得:,
根据外角性质得:,,
则,
则.
故答案为:.
17.【答案】
【解析】【分析】
本次考查了平行线的性质和三角形内角和定理根据两副直角三角板直角边重合得到边平行于边,根据平行线内错角相等判断出 ,再根据三角形的内角和定理与平角的定义求出.
【解答】
解:如图:根据两副直角三角板直角边重合得垂直,垂直,得,
,
,
在中,,
.
故答案为.
18.【答案】
【解析】【分析】
此题主要考查了三角形内角和定理以及角平分线的定义,熟练应用角平分线的性质是解题关键.
根据三角形内角和定理、角平分线的定义以及三角形外角定理求得;最后在中利用三角形内角和定理可以求得的度数.
【解答】
解:三角形的外角和的平分线交于点,
,;
又已知,三角形内角和定理,
外角定理,
.
故答案为.
19.【答案】
【解析】解:如图,点是的中点,
在中以为底,在中以为底,且,而高相等,
,
是的中点,
,
,且,
,
即阴影部分的面积为.
故答案为.
因为点是的中点,所以的底是的底的一半,高等于的高;同理,、、分别是、的中点,可得的面积是面积的一半;利用三角形的等积变换可解答.
本题主要考查了三角形面积的等积变换:若两个三角形的高或底相等,其中一个三角形的底或高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.
20.【答案】
【解析】【分析】
本题考查了三角形内角和定理,三角形外角与内角的关系及等腰三角形的性质的综合运用.充分利用外角的性质推出与的关系是正确解答本题的关键.
由根据三角形内角和公式可求得的度数,再根据等腰三角形的性质及三角形外角的性质推出与的关系即可解答.
【解答】
解:,,
,,
,
是的外角,
.
故答案为.
21.【答案】解:在中,,,
.
是的平分线,
,,
.
,
.
【解析】本题考查了三角形的角平分线的定义、三角形外角的性质、平行线的性质及三角形内角和定理,
先由三角形外角的性质求出的度数,再根据角平分线的定义即可得到答案;
由内角和定理求出的度数,再根据两直线平行同位角相等即可得到答案.
22.【答案】证明:过点作,
,
,.
,
.
即.
【解析】本题考查了三角形的内角和定理的证明,作辅助线把三角形的三个内角转化到一个平角上是解题的关键.
过点作,利用,可得,,而,利用等量代换可证.
23.【答案】解:于点
【解析】本题考查了三角形内角和定理,三角形外角的性质,灵活应用三角形内角和计算角度是解题的关键。
先利用垂直的定义得到,根据三角形内角和定理计算出,再利用对顶角相等得,最后根据三角形外角性质计算的度数。
24.【答案】解:连接并延长至点,如图.
,.
,,,
.
,
这个零件不合格.
【解析】本题考查了三角形外角的性质,主要利用三角形的一个外角等于和它不相邻的两个内角的和的性质,
熟练掌握性质是解题的关键.连接并延长,根据三角形的一个外角等于和它不相邻的两个内角的和求出,,然后求出的度数,根据零件规定数据,只有才是合格产品.
25.【答案】解:,且中有两个内角相等,
,
是由翻折得到,,
,
;
设,
,,
,
中有两个内角相等,可分三种情况讨论:
当时,令,则方程无解,
此情况不成立,舍去;
当时,令,
解得,
;
当时,令,
解得,
,
综上所述,若中也有两个内角相等,则的度数可能为或.
【解析】本题主要考查了分类讨论思想、折叠问题以及三角形内角和定理,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
依据,且中有两个内角相等,可得,再根据折叠的性质,即可得到的度数;
设,即可得到,,,再分三种情况讨论,即可得到的度数可能为或.
第十一章三角形
一、选择题
1.以下列各组线段为边,能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
2.已知一个多边形的内角和是外角和的倍,则这个多边形是( )
A. 八边形 B. 九边形 C. 十边形 D. 十二边形
3.若正多边形的内角和是,则该正多边形的一个外角为( )
A. B. C. D.
4.如图,等于( )
A. B. C. D.
5.如图,在中,是边上的高,平分交边于,,,则的大小是( )
A.
B.
C.
D.
6.将一副三角尺按如图摆放,点在上,点在的延长线上,,,,,则的度数是( )
A. B. C. D.
7.如图,,直线平移后得到直线,则( )
A. B. C. D.
8.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则图中的度数为( )
A.
B.
C.
D.
9.如图,是边的中线,、分别是、的中点,若的面积为,则的面积等于( )
A.
B.
C.
D.
10.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
二、填空题
11.三角形的三边长分别为,,,则的取值范围是 .
12.一个边形的内角和是它外角和的倍,则边数______.
13.小明发现交通指示牌中“停车让行标志”可以看成是正八边形,如图所示,则______
14.在中,若,则是_____________三角形.
15.图是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图是从图冰裂纹窗格图案中提取的由五条线段组成的图形,则 度.
16.如图,在中,,将沿着直线折叠,点落在点的位置,则的度数是 .
17.将一副直角三角板如图放置,使含角的三角板的较短的直角边和含角的三角板的一条直角边重合,则的度数为 度
18.如图,在中,,三角形的外角和的平分线交于点,则 .
19.如图,在中,已知点,,分别为边,,的中点,且的面积等于,则阴影部分图形面积等于______.
20.如图,已知,,,,,则 度.
三、解答题
21.如图,在中,,,的外角的平分线交的延长线于点.
求的度数;
过点作,交的延长线于点,求的度数.
22.已知:如图,是任意一个三角形,求证:.
23.如图,已知于点,且,,求的度数.
24.一个零件的形状如图所示,按规定应等于,,应分别等于,,但检验工人测得,就断定这个零件不合格,这是为什么呢
25.如图,直角三角形纸片中,,将纸片沿折叠,使得点落在上点处,连接,中有两个内角相等.
若,求的度数;若中也有两个内角相等,求的度数.
答案和解析
1.【答案】
【解析】【分析】
根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
【解答】
解:根据三角形的三边关系,知:
A、,不能组成三角形;
B、,不能组成三角形;
C、,不能组成三角形;
D、,能够组成三角形.
故选:.
2.【答案】
【解析】解:设这个多边形的边数为,则该多边形的内角和为,
依题意得,
解得,
这个多边形的边数是.
故选:.
先设这个多边形的边数为,得出该多边形的内角和为,根据多边形的内角和是外角和的倍,列方程求解.
本题主要考查了多边形内角和定理与外角和定理,多边形内角和且为整数,而多边形的外角和指每个顶点处取一个外角,则边形取个外角,无论边数是几,其外角和始终为.
3.【答案】
【解析】【分析】
本题主要考查了多边形的内角和与外角和之间的关系,关键是记住内角和的公式与外角和的特征,难度适中.
根据多边形的内角和公式求出多边形的边数,再根据多边形的外角和是固定的,依此可以求出多边形的一个外角.
【解答】
解:正多边形的内角和是,
多边形的边数为,
多边形的外角和都是,
多边形的每个外角.
故选:.
4.【答案】
【解析】【分析】
本题考查的是三角形外角的性质及三角形内角和定理,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.
先根据三角形外角的性质得出及的度数,再由三角形内角和定理即可得出结论.
【解答】
解:如图,
是的外角,
;
是的外角,
,
,
.
故选D.
5.【答案】
【解析】【分析】
本题考查了三角形的内角和定理,角平分线的定义,准确识图理清图中各角度之间的关系是解题的关键.
根据角平分线的定义可得,再根据直角三角形两锐角互余求出,然后根据计算即可得解.
【解答】
解:平分,
,
是边上的高,
,
.
故选B.
6.【答案】
【解析】【分析】
本题考查了三角形的内角和定理,平行线的性质,以及三角形的外角性质,牢记“两直线平行,内错角相等”是解题的关键.
根据三角形的内角和定理,得,,根据可得,根据三角形的外角性质得,进而可得答案.
【解答】
解:,,
.
,,
.
,
,
,
.
故选A.
7.【答案】
【解析】【分析】
此题考查了平移的性质,平行线的性质,以及三角形外角的性质,熟练掌握平移的性质是解本题的关键.
由平移的性质得到与平行,利用两直线平行同旁内角互补以及三角形外角性质,即可求出所求.
【解答】
解:如图,
直线平移后得到直线,
,
,
,
,
,,
.
故选C.
8.【答案】
【解析】解:,
,
,
又,
,
故选:。
由邻补角概念和翻折变换性质得出,据此知,结合知,从而得出答案。
本题主要考查翻折变换的性质,解题的关键是掌握翻折变换的对应边、对应角相等的性质及直角三角形两锐角互余、对顶角相等的性质。
9.【答案】
【解析】【分析】
本题考查了三角形的面积公式,掌握三角形的中线把三角形的面积分成相等的两部分是解题的关键.
由于是的中点,,那么和可看作等底同高的两个三角形,根据三角形的面积公式,得出和的面积相等,进而得出的面积等于的面积的倍;同理,由于是的中点,得出的面积等于面积的倍;由于是边上的中线,得出的面积等于面积的倍,代入求解即可.
【解答】
解:是的中点,
,
,
又,
.
同理,.
10.【答案】
【解析】【解答】
解:是中的平分线,是的外角的平分线,
,,
,,
,
,
,
,
,
,
故选:.
【分析】
根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出的度数,根据补角的定义求出的度数,根据三角形的内角和即可求出的度数,即可求出结果.
本题考查了角平分线的定义,一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为,难度适中.
11.【答案】
【解析】【分析】
此题主要考查了三角形的三边关系,属于基础题.
根据三角形的三边关系,可得,再解即可.
【解答】
解:根据三角形的三边关系可得:,
解得:.
故答案为.
12.【答案】
【解析】【分析】
本题主要考查了多边形的内角和的计算公式以及多边形的外角和定理,比较简单.
利用多边形的外角和是,一个边形的内角和等于它外角和的倍,则内角和是,而边形的内角和是,则可得到方程,解之即可.
【解答】
解:设多边形的边数为,
根据题意列方程,得:
,
解得:,
故答案为.
13.【答案】
【解析】解:“停车让行标志”可以看成是正八边形,
;
故答案为:.
根据多边形的外角和是,个外角都相等,即可求出.
此题考查了多边形内角与外角,熟练掌握多边形的外角和是是解题的关键.
14.【答案】直角
【解析】【分析】
本题考查了三角形的内角和定理及直角三角形的判定先设,则,,再根据三角形内角和定理列方程,解方程求出三个角的度数即可判断.
【解答】
解:,
设,则,,
,
,
解得,
,,,
是直角三角形.
故答案为直角.
15.【答案】
【解析】【分析】
本题考查的是多边形的外角和,掌握多边形的外角和等于是解题的关键.
根据多边形的外角和等于解答即可.
【解答】
解:由多边形的外角和等于可知,
.
16.【答案】
【解析】【分析】
此题考查了翻折变换折叠问题以及三角形外角性质,熟练掌握折叠的性质是解本题的关键.
由折叠的性质得到,再利用外角性质即可求出所求角的度数.
【解答】
解:
由折叠的性质得:,
根据外角性质得:,,
则,
则.
故答案为:.
17.【答案】
【解析】【分析】
本次考查了平行线的性质和三角形内角和定理根据两副直角三角板直角边重合得到边平行于边,根据平行线内错角相等判断出 ,再根据三角形的内角和定理与平角的定义求出.
【解答】
解:如图:根据两副直角三角板直角边重合得垂直,垂直,得,
,
,
在中,,
.
故答案为.
18.【答案】
【解析】【分析】
此题主要考查了三角形内角和定理以及角平分线的定义,熟练应用角平分线的性质是解题关键.
根据三角形内角和定理、角平分线的定义以及三角形外角定理求得;最后在中利用三角形内角和定理可以求得的度数.
【解答】
解:三角形的外角和的平分线交于点,
,;
又已知,三角形内角和定理,
外角定理,
.
故答案为.
19.【答案】
【解析】解:如图,点是的中点,
在中以为底,在中以为底,且,而高相等,
,
是的中点,
,
,且,
,
即阴影部分的面积为.
故答案为.
因为点是的中点,所以的底是的底的一半,高等于的高;同理,、、分别是、的中点,可得的面积是面积的一半;利用三角形的等积变换可解答.
本题主要考查了三角形面积的等积变换:若两个三角形的高或底相等,其中一个三角形的底或高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.
20.【答案】
【解析】【分析】
本题考查了三角形内角和定理,三角形外角与内角的关系及等腰三角形的性质的综合运用.充分利用外角的性质推出与的关系是正确解答本题的关键.
由根据三角形内角和公式可求得的度数,再根据等腰三角形的性质及三角形外角的性质推出与的关系即可解答.
【解答】
解:,,
,,
,
是的外角,
.
故答案为.
21.【答案】解:在中,,,
.
是的平分线,
,,
.
,
.
【解析】本题考查了三角形的角平分线的定义、三角形外角的性质、平行线的性质及三角形内角和定理,
先由三角形外角的性质求出的度数,再根据角平分线的定义即可得到答案;
由内角和定理求出的度数,再根据两直线平行同位角相等即可得到答案.
22.【答案】证明:过点作,
,
,.
,
.
即.
【解析】本题考查了三角形的内角和定理的证明,作辅助线把三角形的三个内角转化到一个平角上是解题的关键.
过点作,利用,可得,,而,利用等量代换可证.
23.【答案】解:于点
【解析】本题考查了三角形内角和定理,三角形外角的性质,灵活应用三角形内角和计算角度是解题的关键。
先利用垂直的定义得到,根据三角形内角和定理计算出,再利用对顶角相等得,最后根据三角形外角性质计算的度数。
24.【答案】解:连接并延长至点,如图.
,.
,,,
.
,
这个零件不合格.
【解析】本题考查了三角形外角的性质,主要利用三角形的一个外角等于和它不相邻的两个内角的和的性质,
熟练掌握性质是解题的关键.连接并延长,根据三角形的一个外角等于和它不相邻的两个内角的和求出,,然后求出的度数,根据零件规定数据,只有才是合格产品.
25.【答案】解:,且中有两个内角相等,
,
是由翻折得到,,
,
;
设,
,,
,
中有两个内角相等,可分三种情况讨论:
当时,令,则方程无解,
此情况不成立,舍去;
当时,令,
解得,
;
当时,令,
解得,
,
综上所述,若中也有两个内角相等,则的度数可能为或.
【解析】本题主要考查了分类讨论思想、折叠问题以及三角形内角和定理,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
依据,且中有两个内角相等,可得,再根据折叠的性质,即可得到的度数;
设,即可得到,,,再分三种情况讨论,即可得到的度数可能为或.
