湘教版数学八年级上册(新) 习题课课件:5.2《二次根式的乘除》(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级上册(新) 习题课课件:5.2《二次根式的乘除》(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 684.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-13 20:56:35 | ||
图片预览





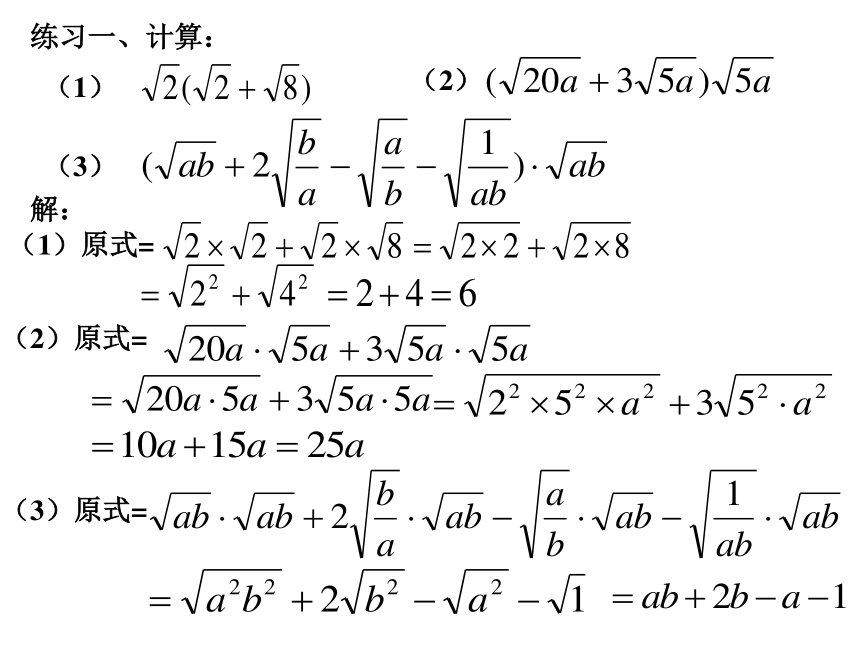
文档简介
课件13张PPT。二次根式的乘除
习题课 一、复习:
1、填空:
(1)二次根式的乘法法则用式子表示为
(2)二次根式的除法法则用式子表示为
(3)把分母中的 化去,叫做分母有理化。将式子
分母有理化后等于 .
(4) 成立的条件是 .
(5) 成立的条件是 .
(6) 成立的条件是 .
(7)化简: 根号(8)计算:2、判断题:下列运算是否正确.( )( )( )( )( )( )( ) ( )3、你能用几种方法将式子化简? 答:可以用三种方法:
(1)将分子与分母乘以同一个代数式,使分母有理化,即(2)利用关系式 ,把分子与分母中的公因式直接约分,即(3)运用二次根式的除法运算,即1、运用乘法分配律进行简单的根式运算 .二、新课:例1 计算 (1) (2)(2)原式 =解:(1) 原式=练习一、计算:(1)(2)(3)(2)原式=(3)原式=2、比较两个实数的大小: 两个正数中,较大的正数,它的算术平方根也较大,即a>b>0时,可以得出 .例2 比较下列两个数的大小.(2)因为又因为18>12,所以 . 即练习二、比较下列各组中两个数的大小所以例3、 计算(1)(2)(2)原式=(2)原式=4、运用分母有理化进行计算.例4、化简 分析:当分母里二次根式的被开方数都相差1时,如果分母有理化后则变为1或-1,就可将原式变为不含分母的二次根式. 解:原式=思考题:计算 2、在进行二次根式的乘除法混合算时, 如果没有括号, 应按从左到右的顺序进行运算,运算结果要注意化简,使被开方数中每个因式(或因数)的指数都小于2. 3、分母有理化的关键是找出分子与分母同乘以一个怎样的代数式, 才能使分母变为有理式(或有理数).它的理论根据是分式的基本性质.三、小结:
1、二次根式的乘法公式
(a≥0,b≥0),由左到右是先乘再开方,由右到左是先开方再乘,运用此公式可以进行二次根式的化简和计算. 运用公式时, 要根据题目以简便为准.
习题课 一、复习:
1、填空:
(1)二次根式的乘法法则用式子表示为
(2)二次根式的除法法则用式子表示为
(3)把分母中的 化去,叫做分母有理化。将式子
分母有理化后等于 .
(4) 成立的条件是 .
(5) 成立的条件是 .
(6) 成立的条件是 .
(7)化简: 根号(8)计算:2、判断题:下列运算是否正确.( )( )( )( )( )( )( ) ( )3、你能用几种方法将式子化简? 答:可以用三种方法:
(1)将分子与分母乘以同一个代数式,使分母有理化,即(2)利用关系式 ,把分子与分母中的公因式直接约分,即(3)运用二次根式的除法运算,即1、运用乘法分配律进行简单的根式运算 .二、新课:例1 计算 (1) (2)(2)原式 =解:(1) 原式=练习一、计算:(1)(2)(3)(2)原式=(3)原式=2、比较两个实数的大小: 两个正数中,较大的正数,它的算术平方根也较大,即a>b>0时,可以得出 .例2 比较下列两个数的大小.(2)因为又因为18>12,所以 . 即练习二、比较下列各组中两个数的大小所以例3、 计算(1)(2)(2)原式=(2)原式=4、运用分母有理化进行计算.例4、化简 分析:当分母里二次根式的被开方数都相差1时,如果分母有理化后则变为1或-1,就可将原式变为不含分母的二次根式. 解:原式=思考题:计算 2、在进行二次根式的乘除法混合算时, 如果没有括号, 应按从左到右的顺序进行运算,运算结果要注意化简,使被开方数中每个因式(或因数)的指数都小于2. 3、分母有理化的关键是找出分子与分母同乘以一个怎样的代数式, 才能使分母变为有理式(或有理数).它的理论根据是分式的基本性质.三、小结:
1、二次根式的乘法公式
(a≥0,b≥0),由左到右是先乘再开方,由右到左是先开方再乘,运用此公式可以进行二次根式的化简和计算. 运用公式时, 要根据题目以简便为准.
同课章节目录
