必修第一册苏教版第5章单元测试卷(含解析)
文档属性
| 名称 | 必修第一册苏教版第5章单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-05 10:11:59 | ||
图片预览




文档简介
第5章 函数概念与性质 单元测试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数f(x)=的定义域为 ( )
A.{x|x>1} B.{x|x<-1} C.{x|-12.已知≈1.414 21,如果对应关系f将n对应到的小数点后第n位上的数字,则f(2)+f(4)= ( )
A.5 B.6 C.3 D.2
3.函数y=的值域是 ( )
A.(-1,] B.(-1,1) C.(-∞,] D.(-2,2)
4.函数g(x)=f(x)-f(-x)+1的图象可能是( )
A B C D
5.已知f(x)是定义在(-2,2)上的奇函数,且在(-2,2)上为增函数,若f(2+a)+f(1-2a)>0,则实数a的取值范围为 ( )
A.(-,0) B.(-∞,3) C.(-4,0) D.(-,)
6.已知函数f(x)=设F(x)=x2·f(x),则对F(x)的描述正确的是 ( )
A.是奇函数,在(-∞,+∞)上单调递减
B.是奇函数,在(-∞,+∞)上单调递增
C.是偶函数,在(-∞,0)上单调递减,在(0,+∞)上单调递增
D.是偶函数,在(-∞,0)上单调递增,在(0,+∞)上单调递减
7.已知定义在R上的函数y=f(x)同时满足下列三个条件:
①对于任意的x∈R都有f(x+4)=f(x);
②对于任意的0≤x1③函数y=f(x+2)的图象关于y轴对称.
则f(5),f(6.5),f(15.5)的大小关系为 ( )
A.f(6.5)>f(5)>f(15.5) B.f(15.5)>f(6.5)>f(5)
C.f(5)>f(6.5)>f(15.5) D.f(6.5)>f(15.5)>f(5)
8.已知函数f(x)=若存在唯一的整数x,使得(2 022f(x)-2 021)(x-a)<0成立,则所有满足条件的整数a的取值集合为 ( )
A.{-2,0,1,2} B.{-2,-1,0,1} C.{-1,0,1,2} D.{-1,0,1}
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列各对函数中,图象完全相同的是 ( )
A.y=x与y= B.y=()2与y=|x|
C.y=与y=x0 D.y=与y=
10.已知函数f(x)的定义域为R,对任意的实数x,y满足f(x+y)=f(x)+f(y)+,且f()=0,下列结论正确的是 ( )
A.f(0)=- B.f(-1)=-
C.f(x)为R上的减函数 D.f(x)+为奇函数
11.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设x∈R,用[x]表示不超过x的最大整数,称y=[x]为高斯函数,如:[1.2]=1,[-1.2]=-2,因而y=[x]又被称为取整函数,在现实生活中有着广泛的应用,诸如停车收费,出租车收费等均按“取整函数”进行计费.以下关于“取整函数”的描述,正确的是 ( )
A. x∈R,[2x]=2[x] B. x∈R,[x]+[x+]=[2x]
C. x,y∈R,若[x]=[y],则有x-y>-1 D.方程x2=3[x]+1的解集为{,}
三、填空题:本题共3小题,每小题5分,共15分.
12.若g(x)=x-1,f(g(x))=,则f(1)= .
13.已知f (x+2)是偶函数,f(x)在(-∞,2]上单调递减,f(0)=0,则f(2-3x)>0的解集是 .
14.设函数f(x)=
(1)若 x∈R且x≠0,使得f(1+x)=f(1-x)成立,则实数a的取值范围是 ;
(2)若函数f(x)为R上的单调函数,则实数a的取值范围是 .(本题第一空2分,第二空3分)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)(1)用定义法证明函数f(x)=x2-在(0,+∞)上单调递增;
(2)已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=x3+3x2+1,求g(x)的解析式.
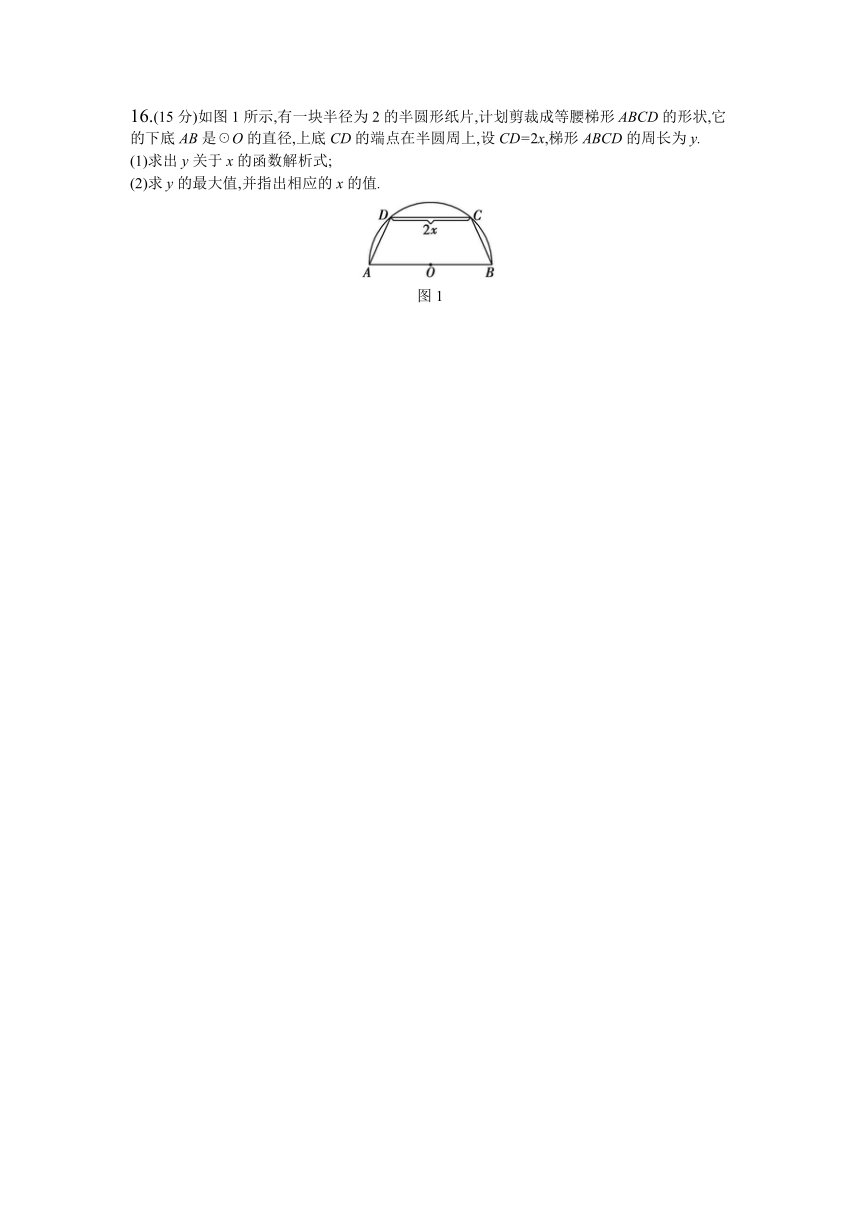
16.(15分)如图1所示,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是☉O的直径,上底CD的端点在半圆周上,设CD=2x,梯形ABCD的周长为y.
(1)求出y关于x的函数解析式;
(2)求y的最大值,并指出相应的x的值.
图1
17.(15分)已知函数f(x)=的定义域是(-1,1).
(1)当b=2时,求f(x)的值域;
(2)当b=0时,解不等式f(t-1)+f(t)<0.
18.(17分)有三个条件:①f(x+1)=f(x)+2x-1;②f(x+1)=f(1-x)且f(0)=3;③f(x)的最小值为2且f(0)=3.
从这三个条件中任选一个,补充在下面的问题中,并作答.
问题:已知二次函数f(x)满足 ,f(1)=2.
(1)求f(x)的解析式;
(2)设函数g(x)=f(x),x∈[-1,4],求g(x)的最值.
注:若选择多个条件分别进行解答,则按第一个解答计分.
19.(17分)定义:设函数f(x)的定义域为D,若存在实数m,M,对任意的实数x∈D,有f(x)≤M,则称函数f(x)为有上界函数,M是f(x)的一个上界;有f(x)≥m,则称函数f(x)为有下界函数,m是f(x)的一个下界.
(1)若函数f(x)=x2+cx-2在(0,1)上是以2为上界的有界函数,求实数c的取值范围.
(2)某同学在研究函数y=x+(b>0)的单调性时发现该函数在(0,]与[,+∞)上具有单调性,
(i)请直接写出函数y=x+(b>0)在(0,]与[,+∞)上的单调性,不必证明;
(ii)若函数g(x)=(a>0)的定义域为[4,16],m是函数g(x)的下界,请利用(i)的结论,求m的最大值m(a).
第5章 函数概念与性质 单元测试卷 参考答案
1.D 因为f(x)是分式,所以函数f(x)的定义域是使分母不等于零的实数,故x2-1≠0,即x≠±1,所以函数的定义域为{x|x≠±1}.
2.C 根据题意,对应关系f将n对应到的小数点后第n位上的数字,则f(2)=1,f(4)=2,则f(2)+f(4)=3,故选C.
3.A 函数y===-1+,
∵0<≤,∴-14.C 令h(x)=f(x)-f(-x),则g(x)=h(x)+1,g(x)的图象就是将h(x)的图象向上平移一个单位,
因为h(-x)=f(-x)-f(x)=-h(x),所以函数h(x)为奇函数,图象关于原点对称,
所以g(x)=f(x)-f(-x)+1的图象关于点(0,1)对称.
结合选项可知C正确.
5.A ∵f(2+a)+f(1-2a)>0,∴f(2+a)>-f(1-2a).
又f(x)为奇函数,∴f(2+a)>f(2a-1).
∵f(x)在(-2,2)上为增函数,∴
解得-6.B ∵f(-x)=∴f(-x)=-f(x),∴f(x)为奇函数.
∵F(x)=x2·f(x),
∴F(-x)=(-x)2·f(-x)=-x2·f(x)=-F(x),
∴F(x)是奇函数,可排除C,D.
又F(x)=x2·f(x)=
∴F(x)在(-∞,+∞)上单调递增.故选B.
7.A 由f(x+4)=f(x)可知,f(6.5)=f(2.5),f(5)=f(1),
f(15.5)=f(3.5).
因为函数y=f(x+2)的图象关于y轴对称,且y=f(x)的图象向左平移2个单位长度可得y=f(x+2)的图象,
所以y=f(x)的图象关于直线x=2对称,则有f(6.5)=f(2.5)=f(1.5),f(15.5)=f(3.5)=f(0.5).
对于任意的0≤x1f(1)>f(0.5),即f(6.5)>f(5)>f(15.5).
8.B 作出函数f(x)的图象,如图D 1所示,
图D 1
对于(2 022f(x)-2 021)(x-a)<0,
当2 022f(x)-2 021<0,即f(x)<时,x-a>0,即x>a,记A={x|x>a},
对于f(x)<,则或且x∈Z,
可得f(x)<的整数解集为B={x∈Z|x≤-2或x=0}.
由题意可得,集合A∩B只有一个元素,即A∩B={0},则
-2≤a<0,
满足条件的整数a的取值为-2,-1.
当2 022f(x)-2 021>0,即f(x)>时,x-a<0,即x对于f(x)>,则或且x∈Z,
可得f(x)>的整数解集为D={x∈Z|x≥1或x=-1},
由题意可得,集合C∩D只有一个元素,即C∩D={-1},则-1满足条件的整数a的取值为0,1.
综上所述,所有满足条件的整数a的取值集合为{-2,-1,0,1}.
9.AC 对于A,∵y=x的定义域为R,y=的定义域为R,两个函数的对应关系相同,∴是同一个函数.对于B,∵y=()2的定义域为[0,+∞),y=|x|的定义域为R,∴两个函数不是同一个函数.对于C,∵y=的定义域为(-∞,0)∪(0,+∞),y=x0的定义域为(-∞,0)∪(0,+∞),两个函数的对应关系相同,∴两个函数是同一个函数.对于D,y=的定义域是{x|x≠±1},y=的定义域是{x|x≠1},定义域不相同,∴不是同一个函数.
10.ABD 依题意f(x+y)=f(x)+f(y)+,且f()=0,
令x=y=0,得f(0+0)=f(0)+f(0)+,所以f(0)=-,故A选项正确.
令x=,y=-,则f(-)=f()+f(-)+,
即-=0+f(-)+,所以f(-)=-1,
令x=y=-,得f(--)=f(-)+f(-)+,
即f(-1)=2f(-)+=-2+=-,故B选项正确.
由于f(-1)令y=-x,得f(x-x)=f(x)+f(-x)+,即-=f(x)+f(-x)+,即0=[f(x)+]+[f(-x)+],所以f(x)+为奇函数,故D选项正确.故选ABD.
11.BCD 对于A,取x=,则[2x]=[1]=1,2[x]=2[]=0,故A错误.对于B,设[x]=x-a,a∈[0,1),所以[x]+[x+]=[x]+[[x]+a+]=2[x]+[a+],[2x]=[2[x]+2a]=2[x]+[2a],当a∈[0,)时,a+∈[,1),2a∈[0,1),则[a+]=0,[2a]=0,则[x]+[x+]=2[x],[2x]=2[x],故当a∈[0,)时,[x]+[x+]=[2x]成立;当a∈[,1)时,a+∈[1,),2a∈[1,2),则[a+]=1,[2a]=1,则[x]+[x+]=2[x]+1,[2x]=2[x]+1,故当a∈[,1)时,[x]+[x+]=[2x]成立,综上B正确.对于C,设[x]=[y]=m,则x=m+t,0≤t<1,y=m+s,0≤s<1,则|x-y|=|(m+t)-(m+s)|=|t-s|<1,因此x-y>-1,故C正确.对于D,由x2=3[x]+1知,x2一定为整数且3[x]+1≥0,所以[x]≥-,所以[x]≥0,所以x≥0,由[x]2≤x2<([x]+1)2,得[x]2≤3[x]+1<([x]+1)2,由[x]2≤3[x]+1,解得≤[x]≤≈3.3,只能取0≤[x]≤3,由3[x]+1<([x]+1)2,解得[x]>1或[x]<0(舍去),故2≤[x]≤3,所以[x]=2或[x]=3,当[x]=2时,x=,当[x]=3时,x=,所以方程x2=3[x]+1的解集为{,},故D正确.故选BCD.
12.1 在f(g(x))=中,令x=2可得f(g(2))=f(1)==1.
14.(-∞,-)∪(,+∞) 因为f(x+2)是偶函数,所以f(x+2)=f(-x+2),f(x)的图象关于直线x=2对称,
由f(0)=0得f(4)=0,又f(x)在(-∞,2]上单调递减,所以f(x)在[2,+∞)上单调递增,
所以f(2-3x)>0,即2-3x<0或2-3x>4,解得x>或x<-.
因此,f(2-3x)>0的解集是(-∞,-)∪(,+∞).
14.(1)a>1 f(1+x)=f(1-x),即函数f(x)的图象关于直线x=1对称.令g(x)=-x2+2x,易知其图象开口向下,对称轴方程为x=1,可画出f(x)的大致图象(图略).
结合图象易知,若 x∈R且x≠0,使得f(1+x)=f(1-x),则a>1.
(2)a≤0或a=1 g(x)=-x2+2x在(-∞,1)上单调递增,令h(x)=x,则h(x)在R上单调递增,令g(x)≤h(x),则x≤0或x≥1.
结合图象知,若使f(x)在R上为单调函数,则a≤0或a=1.
15.(1)任取x1,x2∈(0,+∞),且x1则f(x1)-f(x2)=--+=(x1+x2)(x1-x2)+=(x1+x2+)(x1-x2).
因为00,所以f(x1)故函数f(x)=x2-在(0,+∞)上单调递增.
(2)当x>0时,-x<0,g(-x)=(-x)3+3(-x)2+1=-x3+3x2+1,
因为g(x)是定义在R上的奇函数,所以g(x)=-g(-x)=x3-3x2-1,且g(0)=0.
故g(x)=
图D 2
16.(1)作OH垂直DC交DC于点H,可知H是DC的中点,作DN垂直AB交AB于点N,连接OD,如图D 2所示.
设 OH=h,则h==.
在Rt△AND中,AD====2,所以y=AB+DC+2AD=4+2x+4,定义域是(0,2).
(2)令t=,则t∈(0,),且x=2-t2,
所以y=4+2(2-t2)+4t=-2(t-1)2+10,
故当t=1即x=1时,y取得最大值,最大值是10.
17.(1)当b=2时,可得f(x)==,
设y===(x+2)+-4,
∵f(x)的定义域是(-1,1),∴1根据对勾函数的性质可得2-4≤y<0,
∴函数f(x)≤,
即f(x)的值域为(-∞,-].
(2)当b=0时,可得f(x)=,则f(-x)=-=-f(x),故f(x)是奇函数.
任取-10,即f(x1)>f(x2),故f(x)在(-1,1)上为减函数.
不等式f(t-1)+f(t)<0,即f(t-1)<-f(t),∴f(t-1)故得解得故不等式的解集为(,1).
18.(1)选择①.
设f(x)=ax2+bx+c(a≠0),则f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c,
∵f(x+1)=f(x)+2x-1,
∴ax2+(2a+b)x+a+b+c=ax2+(b+2)x+c-1,
∴解得a=1,b=-2.
又二次函数f(x)的图象经过点(1,2),∴a+b+c=2,∴c=3,故f(x)的解析式为f(x)=x2-2x+3.
选择②.
设f(x)=ax2+bx+c(a≠0),由f(0)=3,可得c=3.
∵f(x+1)=f(1-x),
∴二次函数f(x)图象的对称轴方程为x=1,即-=1.
又f(x)的图象经过点(1,2),∴a+b+c=2,
解得a=1,b=-2,故f(x)的解析式为f(x)=x2-2x+3.
选择③.
设f(x)=ax2+bx+c(a≠0),由f(0)=3,可得c=3.
∵f(x)≥2恒成立,且f(1)=2,∴f(x)图象的对称轴方程为x=1,即-=1,又f(1)=a+b+c=2,
∴a=1,b=-2,故f(x)的解析式为f(x)=x2-2x+3.
(2)根据(1)可知g(x)=x2-2x+3,x∈[-1,4],结合二次函数性质可知,
g(x)在区间[-1,1]上单调递减,在区间[1,4]上单调递增,
∴g(x)max=g(4)=11,g(x)min=g(1)=2.
故g(x)在[-1,4]上的最小值为2,最大值为11.
19.(1)依题意得,对任意x∈(0,1),x2+cx-2≤2恒成立.
∴c≤-x对任意x∈(0,1)恒成立.
令h(x)=-x,显然函数h(x)=-x在(0,1)上单调递减,
∴当x∈(0,1)时,h(x)>h(1)=3,
∴c≤3,即实数c的取值范围为(-∞,3].
(i)函数y=x+(b>0)在(0,]上为减函数,在[,+∞)上为增函数.
(ii)g(x)==x+(a>0).
①当≥16,即a≥128时,由(i)知g(x)在[4,16]上为减函数,
∴g(x)≥g(16)=16+,
∴m(a)=16+;
②当≤4,即0∴g(x)≥g(4)=4+,
∴m(a)=4+;
③当4<<16,即8当且仅当x=时等号成立,
∴m(a)=2.
综上所述,m(a)=.(17分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数f(x)=的定义域为 ( )
A.{x|x>1} B.{x|x<-1} C.{x|-1
A.5 B.6 C.3 D.2
3.函数y=的值域是 ( )
A.(-1,] B.(-1,1) C.(-∞,] D.(-2,2)
4.函数g(x)=f(x)-f(-x)+1的图象可能是( )
A B C D
5.已知f(x)是定义在(-2,2)上的奇函数,且在(-2,2)上为增函数,若f(2+a)+f(1-2a)>0,则实数a的取值范围为 ( )
A.(-,0) B.(-∞,3) C.(-4,0) D.(-,)
6.已知函数f(x)=设F(x)=x2·f(x),则对F(x)的描述正确的是 ( )
A.是奇函数,在(-∞,+∞)上单调递减
B.是奇函数,在(-∞,+∞)上单调递增
C.是偶函数,在(-∞,0)上单调递减,在(0,+∞)上单调递增
D.是偶函数,在(-∞,0)上单调递增,在(0,+∞)上单调递减
7.已知定义在R上的函数y=f(x)同时满足下列三个条件:
①对于任意的x∈R都有f(x+4)=f(x);
②对于任意的0≤x1
则f(5),f(6.5),f(15.5)的大小关系为 ( )
A.f(6.5)>f(5)>f(15.5) B.f(15.5)>f(6.5)>f(5)
C.f(5)>f(6.5)>f(15.5) D.f(6.5)>f(15.5)>f(5)
8.已知函数f(x)=若存在唯一的整数x,使得(2 022f(x)-2 021)(x-a)<0成立,则所有满足条件的整数a的取值集合为 ( )
A.{-2,0,1,2} B.{-2,-1,0,1} C.{-1,0,1,2} D.{-1,0,1}
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列各对函数中,图象完全相同的是 ( )
A.y=x与y= B.y=()2与y=|x|
C.y=与y=x0 D.y=与y=
10.已知函数f(x)的定义域为R,对任意的实数x,y满足f(x+y)=f(x)+f(y)+,且f()=0,下列结论正确的是 ( )
A.f(0)=- B.f(-1)=-
C.f(x)为R上的减函数 D.f(x)+为奇函数
11.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设x∈R,用[x]表示不超过x的最大整数,称y=[x]为高斯函数,如:[1.2]=1,[-1.2]=-2,因而y=[x]又被称为取整函数,在现实生活中有着广泛的应用,诸如停车收费,出租车收费等均按“取整函数”进行计费.以下关于“取整函数”的描述,正确的是 ( )
A. x∈R,[2x]=2[x] B. x∈R,[x]+[x+]=[2x]
C. x,y∈R,若[x]=[y],则有x-y>-1 D.方程x2=3[x]+1的解集为{,}
三、填空题:本题共3小题,每小题5分,共15分.
12.若g(x)=x-1,f(g(x))=,则f(1)= .
13.已知f (x+2)是偶函数,f(x)在(-∞,2]上单调递减,f(0)=0,则f(2-3x)>0的解集是 .
14.设函数f(x)=
(1)若 x∈R且x≠0,使得f(1+x)=f(1-x)成立,则实数a的取值范围是 ;
(2)若函数f(x)为R上的单调函数,则实数a的取值范围是 .(本题第一空2分,第二空3分)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)(1)用定义法证明函数f(x)=x2-在(0,+∞)上单调递增;
(2)已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=x3+3x2+1,求g(x)的解析式.
16.(15分)如图1所示,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是☉O的直径,上底CD的端点在半圆周上,设CD=2x,梯形ABCD的周长为y.
(1)求出y关于x的函数解析式;
(2)求y的最大值,并指出相应的x的值.
图1
17.(15分)已知函数f(x)=的定义域是(-1,1).
(1)当b=2时,求f(x)的值域;
(2)当b=0时,解不等式f(t-1)+f(t)<0.
18.(17分)有三个条件:①f(x+1)=f(x)+2x-1;②f(x+1)=f(1-x)且f(0)=3;③f(x)的最小值为2且f(0)=3.
从这三个条件中任选一个,补充在下面的问题中,并作答.
问题:已知二次函数f(x)满足 ,f(1)=2.
(1)求f(x)的解析式;
(2)设函数g(x)=f(x),x∈[-1,4],求g(x)的最值.
注:若选择多个条件分别进行解答,则按第一个解答计分.
19.(17分)定义:设函数f(x)的定义域为D,若存在实数m,M,对任意的实数x∈D,有f(x)≤M,则称函数f(x)为有上界函数,M是f(x)的一个上界;有f(x)≥m,则称函数f(x)为有下界函数,m是f(x)的一个下界.
(1)若函数f(x)=x2+cx-2在(0,1)上是以2为上界的有界函数,求实数c的取值范围.
(2)某同学在研究函数y=x+(b>0)的单调性时发现该函数在(0,]与[,+∞)上具有单调性,
(i)请直接写出函数y=x+(b>0)在(0,]与[,+∞)上的单调性,不必证明;
(ii)若函数g(x)=(a>0)的定义域为[4,16],m是函数g(x)的下界,请利用(i)的结论,求m的最大值m(a).
第5章 函数概念与性质 单元测试卷 参考答案
1.D 因为f(x)是分式,所以函数f(x)的定义域是使分母不等于零的实数,故x2-1≠0,即x≠±1,所以函数的定义域为{x|x≠±1}.
2.C 根据题意,对应关系f将n对应到的小数点后第n位上的数字,则f(2)=1,f(4)=2,则f(2)+f(4)=3,故选C.
3.A 函数y===-1+,
∵0<≤,∴-1
因为h(-x)=f(-x)-f(x)=-h(x),所以函数h(x)为奇函数,图象关于原点对称,
所以g(x)=f(x)-f(-x)+1的图象关于点(0,1)对称.
结合选项可知C正确.
5.A ∵f(2+a)+f(1-2a)>0,∴f(2+a)>-f(1-2a).
又f(x)为奇函数,∴f(2+a)>f(2a-1).
∵f(x)在(-2,2)上为增函数,∴
解得-
∵F(x)=x2·f(x),
∴F(-x)=(-x)2·f(-x)=-x2·f(x)=-F(x),
∴F(x)是奇函数,可排除C,D.
又F(x)=x2·f(x)=
∴F(x)在(-∞,+∞)上单调递增.故选B.
7.A 由f(x+4)=f(x)可知,f(6.5)=f(2.5),f(5)=f(1),
f(15.5)=f(3.5).
因为函数y=f(x+2)的图象关于y轴对称,且y=f(x)的图象向左平移2个单位长度可得y=f(x+2)的图象,
所以y=f(x)的图象关于直线x=2对称,则有f(6.5)=f(2.5)=f(1.5),f(15.5)=f(3.5)=f(0.5).
对于任意的0≤x1
8.B 作出函数f(x)的图象,如图D 1所示,
图D 1
对于(2 022f(x)-2 021)(x-a)<0,
当2 022f(x)-2 021<0,即f(x)<时,x-a>0,即x>a,记A={x|x>a},
对于f(x)<,则或且x∈Z,
可得f(x)<的整数解集为B={x∈Z|x≤-2或x=0}.
由题意可得,集合A∩B只有一个元素,即A∩B={0},则
-2≤a<0,
满足条件的整数a的取值为-2,-1.
当2 022f(x)-2 021>0,即f(x)>时,x-a<0,即x
可得f(x)>的整数解集为D={x∈Z|x≥1或x=-1},
由题意可得,集合C∩D只有一个元素,即C∩D={-1},则-1
综上所述,所有满足条件的整数a的取值集合为{-2,-1,0,1}.
9.AC 对于A,∵y=x的定义域为R,y=的定义域为R,两个函数的对应关系相同,∴是同一个函数.对于B,∵y=()2的定义域为[0,+∞),y=|x|的定义域为R,∴两个函数不是同一个函数.对于C,∵y=的定义域为(-∞,0)∪(0,+∞),y=x0的定义域为(-∞,0)∪(0,+∞),两个函数的对应关系相同,∴两个函数是同一个函数.对于D,y=的定义域是{x|x≠±1},y=的定义域是{x|x≠1},定义域不相同,∴不是同一个函数.
10.ABD 依题意f(x+y)=f(x)+f(y)+,且f()=0,
令x=y=0,得f(0+0)=f(0)+f(0)+,所以f(0)=-,故A选项正确.
令x=,y=-,则f(-)=f()+f(-)+,
即-=0+f(-)+,所以f(-)=-1,
令x=y=-,得f(--)=f(-)+f(-)+,
即f(-1)=2f(-)+=-2+=-,故B选项正确.
由于f(-1)
11.BCD 对于A,取x=,则[2x]=[1]=1,2[x]=2[]=0,故A错误.对于B,设[x]=x-a,a∈[0,1),所以[x]+[x+]=[x]+[[x]+a+]=2[x]+[a+],[2x]=[2[x]+2a]=2[x]+[2a],当a∈[0,)时,a+∈[,1),2a∈[0,1),则[a+]=0,[2a]=0,则[x]+[x+]=2[x],[2x]=2[x],故当a∈[0,)时,[x]+[x+]=[2x]成立;当a∈[,1)时,a+∈[1,),2a∈[1,2),则[a+]=1,[2a]=1,则[x]+[x+]=2[x]+1,[2x]=2[x]+1,故当a∈[,1)时,[x]+[x+]=[2x]成立,综上B正确.对于C,设[x]=[y]=m,则x=m+t,0≤t<1,y=m+s,0≤s<1,则|x-y|=|(m+t)-(m+s)|=|t-s|<1,因此x-y>-1,故C正确.对于D,由x2=3[x]+1知,x2一定为整数且3[x]+1≥0,所以[x]≥-,所以[x]≥0,所以x≥0,由[x]2≤x2<([x]+1)2,得[x]2≤3[x]+1<([x]+1)2,由[x]2≤3[x]+1,解得≤[x]≤≈3.3,只能取0≤[x]≤3,由3[x]+1<([x]+1)2,解得[x]>1或[x]<0(舍去),故2≤[x]≤3,所以[x]=2或[x]=3,当[x]=2时,x=,当[x]=3时,x=,所以方程x2=3[x]+1的解集为{,},故D正确.故选BCD.
12.1 在f(g(x))=中,令x=2可得f(g(2))=f(1)==1.
14.(-∞,-)∪(,+∞) 因为f(x+2)是偶函数,所以f(x+2)=f(-x+2),f(x)的图象关于直线x=2对称,
由f(0)=0得f(4)=0,又f(x)在(-∞,2]上单调递减,所以f(x)在[2,+∞)上单调递增,
所以f(2-3x)>0,即2-3x<0或2-3x>4,解得x>或x<-.
因此,f(2-3x)>0的解集是(-∞,-)∪(,+∞).
14.(1)a>1 f(1+x)=f(1-x),即函数f(x)的图象关于直线x=1对称.令g(x)=-x2+2x,易知其图象开口向下,对称轴方程为x=1,可画出f(x)的大致图象(图略).
结合图象易知,若 x∈R且x≠0,使得f(1+x)=f(1-x),则a>1.
(2)a≤0或a=1 g(x)=-x2+2x在(-∞,1)上单调递增,令h(x)=x,则h(x)在R上单调递增,令g(x)≤h(x),则x≤0或x≥1.
结合图象知,若使f(x)在R上为单调函数,则a≤0或a=1.
15.(1)任取x1,x2∈(0,+∞),且x1
因为0
(2)当x>0时,-x<0,g(-x)=(-x)3+3(-x)2+1=-x3+3x2+1,
因为g(x)是定义在R上的奇函数,所以g(x)=-g(-x)=x3-3x2-1,且g(0)=0.
故g(x)=
图D 2
16.(1)作OH垂直DC交DC于点H,可知H是DC的中点,作DN垂直AB交AB于点N,连接OD,如图D 2所示.
设 OH=h,则h==.
在Rt△AND中,AD====2,所以y=AB+DC+2AD=4+2x+4,定义域是(0,2).
(2)令t=,则t∈(0,),且x=2-t2,
所以y=4+2(2-t2)+4t=-2(t-1)2+10,
故当t=1即x=1时,y取得最大值,最大值是10.
17.(1)当b=2时,可得f(x)==,
设y===(x+2)+-4,
∵f(x)的定义域是(-1,1),∴1
∴函数f(x)≤,
即f(x)的值域为(-∞,-].
(2)当b=0时,可得f(x)=,则f(-x)=-=-f(x),故f(x)是奇函数.
任取-1
不等式f(t-1)+f(t)<0,即f(t-1)<-f(t),∴f(t-1)
18.(1)选择①.
设f(x)=ax2+bx+c(a≠0),则f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c,
∵f(x+1)=f(x)+2x-1,
∴ax2+(2a+b)x+a+b+c=ax2+(b+2)x+c-1,
∴解得a=1,b=-2.
又二次函数f(x)的图象经过点(1,2),∴a+b+c=2,∴c=3,故f(x)的解析式为f(x)=x2-2x+3.
选择②.
设f(x)=ax2+bx+c(a≠0),由f(0)=3,可得c=3.
∵f(x+1)=f(1-x),
∴二次函数f(x)图象的对称轴方程为x=1,即-=1.
又f(x)的图象经过点(1,2),∴a+b+c=2,
解得a=1,b=-2,故f(x)的解析式为f(x)=x2-2x+3.
选择③.
设f(x)=ax2+bx+c(a≠0),由f(0)=3,可得c=3.
∵f(x)≥2恒成立,且f(1)=2,∴f(x)图象的对称轴方程为x=1,即-=1,又f(1)=a+b+c=2,
∴a=1,b=-2,故f(x)的解析式为f(x)=x2-2x+3.
(2)根据(1)可知g(x)=x2-2x+3,x∈[-1,4],结合二次函数性质可知,
g(x)在区间[-1,1]上单调递减,在区间[1,4]上单调递增,
∴g(x)max=g(4)=11,g(x)min=g(1)=2.
故g(x)在[-1,4]上的最小值为2,最大值为11.
19.(1)依题意得,对任意x∈(0,1),x2+cx-2≤2恒成立.
∴c≤-x对任意x∈(0,1)恒成立.
令h(x)=-x,显然函数h(x)=-x在(0,1)上单调递减,
∴当x∈(0,1)时,h(x)>h(1)=3,
∴c≤3,即实数c的取值范围为(-∞,3].
(i)函数y=x+(b>0)在(0,]上为减函数,在[,+∞)上为增函数.
(ii)g(x)==x+(a>0).
①当≥16,即a≥128时,由(i)知g(x)在[4,16]上为减函数,
∴g(x)≥g(16)=16+,
∴m(a)=16+;
②当≤4,即0
∴m(a)=4+;
③当4<<16,即8
∴m(a)=2.
综上所述,m(a)=.(17分)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
