3.2.1古典概型
图片预览






文档简介
课件18张PPT。3.2.1 古典 概型新课标人教版数学学科高二年级上学期多媒体教学课件教学要求:1.通过实例,了解基本事件的意义.
2.通过实例,理解古典概型及其概率计算公式.
3.会用列举法计算随机事件包含的基本事件数及事件发生的概率.
4.会初步应用概率计算公式解决简单的古典概型问题.
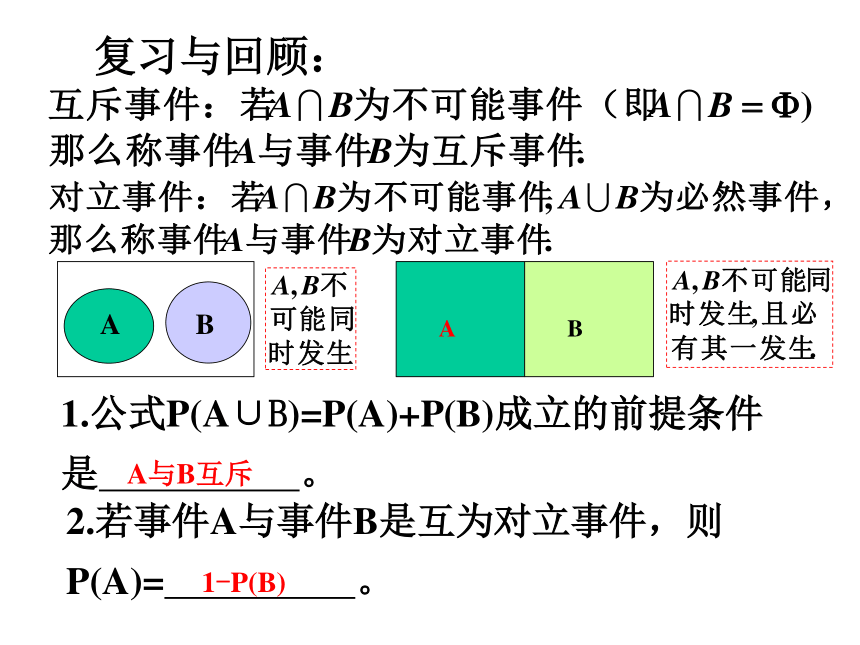
5*.了解随机数的产生,介绍计算器产生两位随机数的方法.教学重点:理解古典概型及其概率计算公式教学难点:设计和运用模拟方法近似计算概率复习与回顾:1.公式P(A∪B)=P(A)+P(B)成立的前提条件是 。2.若事件A与事件B是互为对立事件,则
P(A)= 。A与B互斥1-P(B)例如:在抛掷一枚硬币观察哪个面向上的试验中, “正面朝上”和“反面朝上”这两个事件就是基本事件;又如,在掷骰子的试验中,出现“1点”、“2点”、“3点”、“4点”、“5点”、“6点”这6个事件也是基本事件。 在一个试验可能发生的所有结果中,那些不能再分的最简单的随机事件称为基本事件。(其他事件都可由基本事件来描述)基本事件的特点:
(1)任何两个基本事件是互斥的;
(2)任何事件都可以表示成基本事件的和。 1.什么是“基本事件”?例1.(1)在掷骰子的试验中,事件“出现的点数是2
的倍 数”是哪些基本事件的并事件?
(2)从字母a,b,c,d中任意选出两个不同字母的试
验中,有哪些基本事件?解:(1){出现的点数是2的倍数}
={出现的点数是2}∪{出现的点数是4}∪{出现的点数是6}
(2)所求的基本事件有:
A={a,b}, B={a,c}, C={a,d},
D={b,c}, E={b,d},
F={c,d}。类似抛掷硬币和掷骰子这样的试验,它们都具有以下的共同特点:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等。
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。思考:在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?答:(1)若该古典概型共有n个基本事件,则每一个基本事件发 生的概率都为 P=1/n;
(2)因为每个随机事件都可看成若干个基本事件的并事件,而基本事件之间是互斥的关系,所以若一随机事件是m个基本事件的并事件,则该事件发生的概率为 P=m/n. 2.古典概型的概念3.古典概型下随机事件A发生的概率的计算公式例 在掷骰子的试验中,事件“出现的点数是2的倍数”发生的概率是多少?解:{出现的点数是2的倍数}
={出现的点数是2}∪{出现的点数是4}∪{出现的点数是6}
而这3个基本事件发生的概率都是1/6,所以
P(“出现点数是2的倍数”)
=P(“出现点数是2”)+ P(“出现点数是4”)+ P(“出现点数是6”)
=1/6+1/6+1/6=1/2古典概型事件A发生的概率计算公式:例2. 单选题是标准化考试中常用的题型,一般是从A、
B、C、D四个选项中选择一个正确答案,如果考
生掌握了考察的内容,他可以选择唯一正确的答
案,假设考生不会做,他随机的选择一个答案,
问他答对的概率是多少?解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件只有4个,考生随机选择一个答案即选择A、B、C、D的可能性是相等的,由古典概型的概率计算公式得: 古典概型事件A发生的概率计算公式:探究:在标准化的考试中既有单选题又有不定项选择题,不 定项选择题从A、B、C、D四个选项中选出所有正确 答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?我们探讨正确答案的所有结果:
如果只有一个正确答案是对的,则有4种;
如果有两个答案是正确的,则正确答案可以是(A、B)(A、C)(A、D)(B、C)(B、D) (C、D)6种
如果有三个答案是正确的,则正确答案可以是(A、B、C) (A、B、D) (A、C、D)(B、C、D)4种
所有四个都正确,则正确答案只有1种。
正确答案的所有可能结果有4+6+4+1=15种,从这15种答案中任选一种的可能性只有1/15,因此更难猜对。例3 同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?解:(1)掷一个骰子的结果有6种。我们把两个骰子标上记号1、
2以便区分,由于1号骰子 的每一个结果都可与2号骰子的
任意一个结果配对,组成同时掷两个骰子的一个结果,因
此同时掷两个骰子的结果共有36种。例3 同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?(2)在上面的所有结果中,向上的点数之和为5的结果有
(1,4),(2,3)(3,2)(4,1)
其中第一个数表示1号骰子的结果,第二个数表示2号
骰子的结果。(3)由于所有36种结果是等可能的,其中向上点数之和为5的
结果(记为事件A)有4种,因此,
由古典概型的概率计算公式可得 P(A)=4/36=1/9思考:为什么要把两个骰子标上记号?如果不
标记号会出现什么情况?你能解释其中的原因吗?分析:如果不标记号,类似(1,2)和(2,1)就会没有区别,这样产生的结果就只有1种,其中和是5的就只有两种(1,4),(2,3),所以和为5的概率为解:这个人随机试一个密码,相当做1次随机试验,试验的基本事件(所有可能的结果)共有10 000种.它们是0000,0001,……,9998,9999. 由于假设是随机地试密码,相当于试到任何一个密码可能性是相等的的,所以这是一个古典概型,由计算公式得例4、假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码,问他在自动提款机上随机试一次密码就能取到钱的概率是多少?答:随机试一次密码就能取到钱概率是0.0001。例5、某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽取2听,检测出不合格产品的概率有多大?解:我们把每听饮料标上记号:合格标为:1,2,3,4;不合格的标为a,b. 每次抽取2听,得到的记号标为x和y,则(x,y)表示一次抽取的结果,即基本事件.A表示“抽取的两听饮料中有不合格产品”A1表示“仅第一次抽取不合格产品”A2表示“仅第二次抽取不合格产品”A3表示“两次抽取的都是不合格产品”思考: 随着检测听数的增加,查出不合格产品的概率怎样变化?为什么质检人员都采用抽查的方法而不采用逐个检查的方法?检测的听数和不合格产品的概率如下表:用抽样的方法:节约成本,简单可行,也能达到目的.课堂练习:课本P130 练习1,2,3,练习:1).解:在20瓶饮料中任意抽取1瓶,共有20种取法,
取到过了保质期的只有2种可能,
所以,取到过了保质期的饮料的概率为:2/20=0.1
答:取到过了保质期的饮料的概率为0.1。2).解:在7名同学中任选2名同学,因为被选到的第一位同学有
7种可能,第二位被选到的同学有6种可能,
所以共有 种可能,
同理可得
其中选到的2名同学都去过北京共有 种可能,
所以,选出的2名同学都去过北京的概率为3/21=1/7
答:选出的2名同学都去过北京的概率为1/7。2.古典概型事件A发生的概率计算公式:类似抛掷硬币和掷骰子这样的试验,它们都具有以下的共同特点:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等。
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。 1.古典概型的概念小结:
2.通过实例,理解古典概型及其概率计算公式.
3.会用列举法计算随机事件包含的基本事件数及事件发生的概率.
4.会初步应用概率计算公式解决简单的古典概型问题.
5*.了解随机数的产生,介绍计算器产生两位随机数的方法.教学重点:理解古典概型及其概率计算公式教学难点:设计和运用模拟方法近似计算概率复习与回顾:1.公式P(A∪B)=P(A)+P(B)成立的前提条件是 。2.若事件A与事件B是互为对立事件,则
P(A)= 。A与B互斥1-P(B)例如:在抛掷一枚硬币观察哪个面向上的试验中, “正面朝上”和“反面朝上”这两个事件就是基本事件;又如,在掷骰子的试验中,出现“1点”、“2点”、“3点”、“4点”、“5点”、“6点”这6个事件也是基本事件。 在一个试验可能发生的所有结果中,那些不能再分的最简单的随机事件称为基本事件。(其他事件都可由基本事件来描述)基本事件的特点:
(1)任何两个基本事件是互斥的;
(2)任何事件都可以表示成基本事件的和。 1.什么是“基本事件”?例1.(1)在掷骰子的试验中,事件“出现的点数是2
的倍 数”是哪些基本事件的并事件?
(2)从字母a,b,c,d中任意选出两个不同字母的试
验中,有哪些基本事件?解:(1){出现的点数是2的倍数}
={出现的点数是2}∪{出现的点数是4}∪{出现的点数是6}
(2)所求的基本事件有:
A={a,b}, B={a,c}, C={a,d},
D={b,c}, E={b,d},
F={c,d}。类似抛掷硬币和掷骰子这样的试验,它们都具有以下的共同特点:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等。
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。思考:在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?答:(1)若该古典概型共有n个基本事件,则每一个基本事件发 生的概率都为 P=1/n;
(2)因为每个随机事件都可看成若干个基本事件的并事件,而基本事件之间是互斥的关系,所以若一随机事件是m个基本事件的并事件,则该事件发生的概率为 P=m/n. 2.古典概型的概念3.古典概型下随机事件A发生的概率的计算公式例 在掷骰子的试验中,事件“出现的点数是2的倍数”发生的概率是多少?解:{出现的点数是2的倍数}
={出现的点数是2}∪{出现的点数是4}∪{出现的点数是6}
而这3个基本事件发生的概率都是1/6,所以
P(“出现点数是2的倍数”)
=P(“出现点数是2”)+ P(“出现点数是4”)+ P(“出现点数是6”)
=1/6+1/6+1/6=1/2古典概型事件A发生的概率计算公式:例2. 单选题是标准化考试中常用的题型,一般是从A、
B、C、D四个选项中选择一个正确答案,如果考
生掌握了考察的内容,他可以选择唯一正确的答
案,假设考生不会做,他随机的选择一个答案,
问他答对的概率是多少?解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件只有4个,考生随机选择一个答案即选择A、B、C、D的可能性是相等的,由古典概型的概率计算公式得: 古典概型事件A发生的概率计算公式:探究:在标准化的考试中既有单选题又有不定项选择题,不 定项选择题从A、B、C、D四个选项中选出所有正确 答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?我们探讨正确答案的所有结果:
如果只有一个正确答案是对的,则有4种;
如果有两个答案是正确的,则正确答案可以是(A、B)(A、C)(A、D)(B、C)(B、D) (C、D)6种
如果有三个答案是正确的,则正确答案可以是(A、B、C) (A、B、D) (A、C、D)(B、C、D)4种
所有四个都正确,则正确答案只有1种。
正确答案的所有可能结果有4+6+4+1=15种,从这15种答案中任选一种的可能性只有1/15,因此更难猜对。例3 同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?解:(1)掷一个骰子的结果有6种。我们把两个骰子标上记号1、
2以便区分,由于1号骰子 的每一个结果都可与2号骰子的
任意一个结果配对,组成同时掷两个骰子的一个结果,因
此同时掷两个骰子的结果共有36种。例3 同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?(2)在上面的所有结果中,向上的点数之和为5的结果有
(1,4),(2,3)(3,2)(4,1)
其中第一个数表示1号骰子的结果,第二个数表示2号
骰子的结果。(3)由于所有36种结果是等可能的,其中向上点数之和为5的
结果(记为事件A)有4种,因此,
由古典概型的概率计算公式可得 P(A)=4/36=1/9思考:为什么要把两个骰子标上记号?如果不
标记号会出现什么情况?你能解释其中的原因吗?分析:如果不标记号,类似(1,2)和(2,1)就会没有区别,这样产生的结果就只有1种,其中和是5的就只有两种(1,4),(2,3),所以和为5的概率为解:这个人随机试一个密码,相当做1次随机试验,试验的基本事件(所有可能的结果)共有10 000种.它们是0000,0001,……,9998,9999. 由于假设是随机地试密码,相当于试到任何一个密码可能性是相等的的,所以这是一个古典概型,由计算公式得例4、假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码,问他在自动提款机上随机试一次密码就能取到钱的概率是多少?答:随机试一次密码就能取到钱概率是0.0001。例5、某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽取2听,检测出不合格产品的概率有多大?解:我们把每听饮料标上记号:合格标为:1,2,3,4;不合格的标为a,b. 每次抽取2听,得到的记号标为x和y,则(x,y)表示一次抽取的结果,即基本事件.A表示“抽取的两听饮料中有不合格产品”A1表示“仅第一次抽取不合格产品”A2表示“仅第二次抽取不合格产品”A3表示“两次抽取的都是不合格产品”思考: 随着检测听数的增加,查出不合格产品的概率怎样变化?为什么质检人员都采用抽查的方法而不采用逐个检查的方法?检测的听数和不合格产品的概率如下表:用抽样的方法:节约成本,简单可行,也能达到目的.课堂练习:课本P130 练习1,2,3,练习:1).解:在20瓶饮料中任意抽取1瓶,共有20种取法,
取到过了保质期的只有2种可能,
所以,取到过了保质期的饮料的概率为:2/20=0.1
答:取到过了保质期的饮料的概率为0.1。2).解:在7名同学中任选2名同学,因为被选到的第一位同学有
7种可能,第二位被选到的同学有6种可能,
所以共有 种可能,
同理可得
其中选到的2名同学都去过北京共有 种可能,
所以,选出的2名同学都去过北京的概率为3/21=1/7
答:选出的2名同学都去过北京的概率为1/7。2.古典概型事件A发生的概率计算公式:类似抛掷硬币和掷骰子这样的试验,它们都具有以下的共同特点:
(1) 试验中所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等。
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。 1.古典概型的概念小结:
