2.2 法拉第电磁感应定律 教学课件 (共34张PPT)
文档属性
| 名称 | 2.2 法拉第电磁感应定律 教学课件 (共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-04 14:45:19 | ||
图片预览











文档简介
(共34张PPT)
法拉第电磁感应定律
K
电磁感应现象
实验回顾
N
S
①
②
N
S
N
S
Ф
△Ф
磁通量Ф 磁通量变化△Ф 磁通量变化率与电磁感应的关系
物理意义
与电磁感应的关系
磁通量Ф
穿过回路的磁感线的条数
无关
磁通量变化△Ф
穿过回路的磁通量的变化量
感应电动势产生的条件
磁通量变化率
穿过回路的磁通量的变化快慢
决定感应电动势的大小
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2.磁通量变化越快,感应电动势越大。
磁通量变化
磁通量变化快慢
磁通量
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2.磁通量变化越快,感应电动势越大。
电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(K是一个常数)
(n为线圈的匝数)
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(n为线圈的匝数)
2.数学表达式:
平均磁通变化率
平均感应电动势
例:如图所示,一个50匝的线圈的两端跟R=99Ω的电阻相连接,置于竖直向下的匀强磁场中,线圈的横截面积是20㎝2,电阻为1Ω,磁感应强度以100T/s的变化率均匀减少。在这一过程中通过电阻R的电流为多大?线圈某一横截面内通过的电荷量是多少?
解析:
巩固练习:
√
1.穿过一个单匝线圈的磁通量始终为每秒钟均匀地增加2 Wb,则:
A.线圈中的感应电动势每秒钟增加2 V
B.线圈中的感应电动势每秒钟减少2 V
C.线圈中的感应电动势始终是2 V
D.线圈中不产生感应电动势
三、重要的推论
如图所示闭合线圈一部分导体ab处于匀强磁场中,磁感应强度是B,ab以速度v匀速切割磁感线,求产生的感应电动势。
回路在时间t内增大的面积为:
ΔS=LvΔt
解:
产生的感应电动势为:
穿过回路的磁通量的变化为:
ΔΦ=BΔS
=BLvΔt
G
v
θ
B
V2
V1
=Vsinθ
若导体斜切磁感线
当速度v与磁感应强度B不垂直时,可将B分解为平行于速度分量B||(对感应电动势无贡献),垂直于速度分量B ,则感应电动势:
I
B||
B
B
v
为B、v之间的夹角
感应电动势
L
v
B
公式BLv中的L指的是切割磁感线的有效长度。在上图中E=BLv,L是圆弧切割磁感线的有效长度。
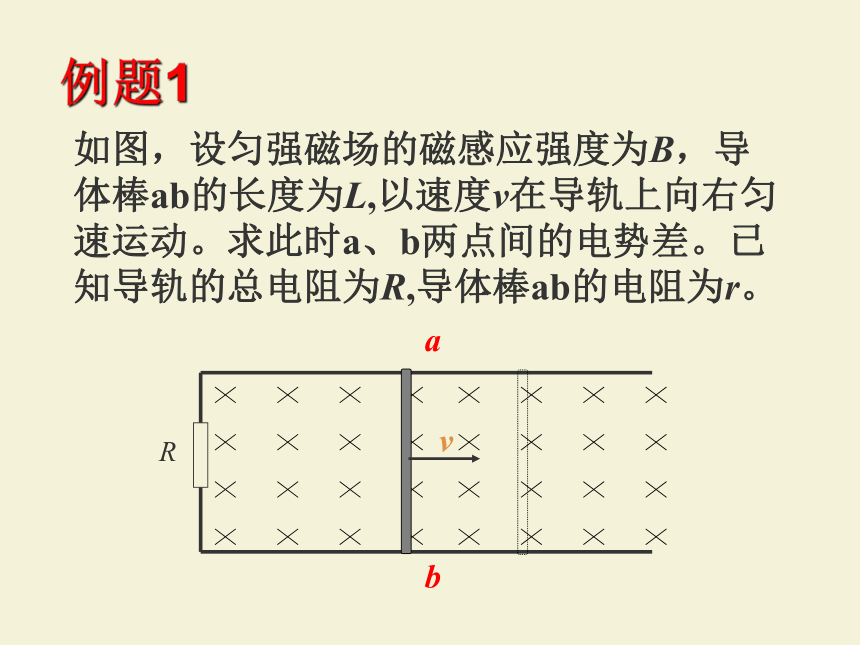
例题1
如图,设匀强磁场的磁感应强度为B,导体棒ab的长度为L,以速度v在导轨上向右匀速运动。求此时a、b两点间的电势差。已知导轨的总电阻为R,导体棒ab的电阻为r。
a
b
v
R
在上题中,导体棒ab的质量为m。若开始导体棒ab在导轨上静止,用一水平向右的恒力F拉导体棒,使它向右运动,试分析导体棒的受力情况、运动情况。求出导体棒运动的最大速度。
a
b
F
V
例题2
a
b
F
运动分析:
F
F安
水平方向受力分析:
F合=F- F安
v
I
F合
a
a=0
N
Y
Vm
当F=F安时,a=0, 此时导体棒最大速度为:
B
G
F安
N
当mgsinθ =F安时,a=0,此时导体棒最大速度为:
拓展
如图所示,长为 的金属杆OA绕过O点垂直于纸面的固定轴沿顺时针方向匀速转动,角速度为ω。一匀强磁场垂直于纸面向里,磁感应强度为B,磁场范围足够大。求OA杆产生感应电动势的大小。
解析:
由于OA杆是匀速转动,故OA产生的感应电动势是恒定的,其平均值与瞬时值相同,求感应电动势的两个公式均可以用。
O
例题3
ω
A
B
C
R
O
例4:如图所示,在磁感应强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架。OC
为一端绕O点在框架上滑动的导体棒,OA之
间连一个阻值为R的电阻(其余电阻都不计),
若使OC以角速度ω匀速转动。试求:
(1)图中哪部分相当于电源?
(2)感应电动势E为多少?
(3)流过电阻R的电流I为多少?
如图所示,边长为a的正方形金属线圈绕通过OO′轴,以角速度ω做匀速转动,匀强磁场的磁感应强度为B,求下列情况的平均感应电动势
1)线框从图示位置转过900
2)线框从图示位置转过1800
3)线框从图示位置转过300
【例题5】线框在磁场中的转动
o
O’
四.反电动势
1.既然线圈在磁场中转动,线圈中就会产生感应电动势。感应电动势加强了电源了产生的电流,还是削弱了它?是有得于线圈的转动,还是阻碍了线圈的转动?
电动机转动是时,线圈中产生的感应电动势
总要削弱电源电动势的作用,阻碍线圈的转动.
──反电动势
2.电动机由于机械故障停转,要立即切断电源。
2.一个矩形线圈,在匀强磁场中绕一个固定轴做匀速转动,当线圈处于如图所示位置时,它的: A.磁通量最大,磁通量变化率最大,感应电动势最大
B.磁通量最小,磁通量变化率最大,感应电动势最大
C.磁通量最大,磁通量变化率最小,感应电动势最大
D.磁通量最小,磁通量变化率最小,感应电动势最大
√
如图所示,导线全部为裸导线,半径为r的圆导线处在垂直于圆平面的匀强磁场中,磁感应强度为B,方向如图。一根长度大于2r的直导线MN,以速率V在圆上自左端匀速滑到右端,电路中定值电阻为R,其余电阻忽略不计。在滑动过程中,通过电阻R的电流的平均值为__________;当MN从圆环左端滑到右端的过程中,通过R的电荷量为_________,当MN通过圆环中心O时,通过R的电流为_________.
(πBrv/2R, πBr2/R,2Brv/R)
应用举例
例1、如图所示为穿过某线路的磁通量Φ随
时间t变化的关系图,试根据图说明:
(1)穿过某线路的磁通量Φ何时最大?
何时最小?
(2)Δφ/Δt何时最大?何时最小?
(3)感应电动势E何时最大?何时最小?
Φ
t
O
t1
t2
t3
t4
注意区分几个物理量:
①Φ、Δφ、Δφ/Δt
②E只与Δφ/Δt有关,
而与Φ、Δφ无关。
思考与讨论:
如图所示,长度都是L、质量都为m的两金属杆ab、cd放在水平
放置的足够长的金属导轨MN、EF上,磁感应强度为B的匀强磁
场强度竖直向上,若ab以速度v向右运动,试回答下列问题:
(不计一切摩擦且导轨足够长)
(1)cd杆将向哪儿动?
(2)两金属杆各做什么性质的运动?
(3)从开始运动直到最后,在金属框架上消耗掉的能量有多少
a
b
d
c
N
F
E
M
B
如图,质量为m,电阻为R,边长为l的正方形线圈从一匀强场区域上方高h处自由下落。设磁场的磁感应强度为B,方向如图,试分析:在线圈下边刚进入磁场到上边尚未进入磁场的过程中,线圈有可能做什么运动,并讨论其条件。
h
l
B
例题5
下落h高度,线框速度为:
若此时线框恰匀速进入磁场,应满足:F安=mg
而F安
线框下落的高度应为:
h0
l
B
v
F安
mg
h0
l
B
v
F安
mg
线框作减速运动,且加速度不断减小
h0
l
B
v
F安
mg
线框作加速运动,且加速度不断减小
讨论
v
t
(1)
(2)
(3)
0
引起磁通量变化的原因
1)稳恒磁场中的导体运动 , 或者回路面积
变化、取向变化等 动生电动势
2)导体不动,磁场变化 感生电动势
电动势
+
-
I
: 非静电的电场强度
动生电动势和感生电动势
+ + + + + + +
+ + + + + + +
+ + + + + + +
+ + + + + + +
+ + + + + + +
O
P
一 动生电动势
动生电动势的非静电力场来源 洛伦兹力
-
- -
++
感应电动势
磁通量 m变
动生电动势
磁场不变,回路面积 S 变
感生电动势
回路不动,磁感应强度变
在磁场中,导体棒AB以 v 沿金属导轨向右运动,导体切割磁力线,回路面积发生变化,导体内产生动生电动势。
自由电子所受的洛仑兹力
产生动生电动势的实质是由于运动导体中的电荷在磁场中受洛仑兹力 fL 的结果。
一、动生电动势的起因
电子感应加速器:在涡旋电场作用下,
电子可以被加速到 10 —100 MeV。
铁
芯
线圈
电
束
子
环形
真空室
B
磁场
基本原理
应用感生电场加速电子的电子感应加速器( betatron ) ,是感生电场存在的最重要的例证之一。
实验装置及原理:
在电磁铁的两极之间安置一个环形真空室,当用交变电流励磁电磁铁时,在环形室内就会感生出很强的、同心环状的有旋电场。用电子枪将电子注入环形室,电子在有旋电场的作用下被加速,并在洛仑兹力的作用下,沿圆形轨道运动。
直流电激励电磁铁:
此时环行真空室中只有恒定的磁场,电子在室内只做匀速圆周运动。
交流电激励电磁铁:
当激励电流增加时,真空室中既有磁场又有有旋电场,电子在其中得到加速。磁场变化越快,电子的加速越明显。
法拉第电磁感应定律
K
电磁感应现象
实验回顾
N
S
①
②
N
S
N
S
Ф
△Ф
磁通量Ф 磁通量变化△Ф 磁通量变化率与电磁感应的关系
物理意义
与电磁感应的关系
磁通量Ф
穿过回路的磁感线的条数
无关
磁通量变化△Ф
穿过回路的磁通量的变化量
感应电动势产生的条件
磁通量变化率
穿过回路的磁通量的变化快慢
决定感应电动势的大小
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2.磁通量变化越快,感应电动势越大。
磁通量变化
磁通量变化快慢
磁通量
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2.磁通量变化越快,感应电动势越大。
电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(K是一个常数)
(n为线圈的匝数)
一、感应电动势
(E)
法拉第电磁感应定律
——感应电动势的大小
电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(n为线圈的匝数)
2.数学表达式:
平均磁通变化率
平均感应电动势
例:如图所示,一个50匝的线圈的两端跟R=99Ω的电阻相连接,置于竖直向下的匀强磁场中,线圈的横截面积是20㎝2,电阻为1Ω,磁感应强度以100T/s的变化率均匀减少。在这一过程中通过电阻R的电流为多大?线圈某一横截面内通过的电荷量是多少?
解析:
巩固练习:
√
1.穿过一个单匝线圈的磁通量始终为每秒钟均匀地增加2 Wb,则:
A.线圈中的感应电动势每秒钟增加2 V
B.线圈中的感应电动势每秒钟减少2 V
C.线圈中的感应电动势始终是2 V
D.线圈中不产生感应电动势
三、重要的推论
如图所示闭合线圈一部分导体ab处于匀强磁场中,磁感应强度是B,ab以速度v匀速切割磁感线,求产生的感应电动势。
回路在时间t内增大的面积为:
ΔS=LvΔt
解:
产生的感应电动势为:
穿过回路的磁通量的变化为:
ΔΦ=BΔS
=BLvΔt
G
v
θ
B
V2
V1
=Vsinθ
若导体斜切磁感线
当速度v与磁感应强度B不垂直时,可将B分解为平行于速度分量B||(对感应电动势无贡献),垂直于速度分量B ,则感应电动势:
I
B||
B
B
v
为B、v之间的夹角
感应电动势
L
v
B
公式BLv中的L指的是切割磁感线的有效长度。在上图中E=BLv,L是圆弧切割磁感线的有效长度。
例题1
如图,设匀强磁场的磁感应强度为B,导体棒ab的长度为L,以速度v在导轨上向右匀速运动。求此时a、b两点间的电势差。已知导轨的总电阻为R,导体棒ab的电阻为r。
a
b
v
R
在上题中,导体棒ab的质量为m。若开始导体棒ab在导轨上静止,用一水平向右的恒力F拉导体棒,使它向右运动,试分析导体棒的受力情况、运动情况。求出导体棒运动的最大速度。
a
b
F
V
例题2
a
b
F
运动分析:
F
F安
水平方向受力分析:
F合=F- F安
v
I
F合
a
a=0
N
Y
Vm
当F=F安时,a=0, 此时导体棒最大速度为:
B
G
F安
N
当mgsinθ =F安时,a=0,此时导体棒最大速度为:
拓展
如图所示,长为 的金属杆OA绕过O点垂直于纸面的固定轴沿顺时针方向匀速转动,角速度为ω。一匀强磁场垂直于纸面向里,磁感应强度为B,磁场范围足够大。求OA杆产生感应电动势的大小。
解析:
由于OA杆是匀速转动,故OA产生的感应电动势是恒定的,其平均值与瞬时值相同,求感应电动势的两个公式均可以用。
O
例题3
ω
A
B
C
R
O
例4:如图所示,在磁感应强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架。OC
为一端绕O点在框架上滑动的导体棒,OA之
间连一个阻值为R的电阻(其余电阻都不计),
若使OC以角速度ω匀速转动。试求:
(1)图中哪部分相当于电源?
(2)感应电动势E为多少?
(3)流过电阻R的电流I为多少?
如图所示,边长为a的正方形金属线圈绕通过OO′轴,以角速度ω做匀速转动,匀强磁场的磁感应强度为B,求下列情况的平均感应电动势
1)线框从图示位置转过900
2)线框从图示位置转过1800
3)线框从图示位置转过300
【例题5】线框在磁场中的转动
o
O’
四.反电动势
1.既然线圈在磁场中转动,线圈中就会产生感应电动势。感应电动势加强了电源了产生的电流,还是削弱了它?是有得于线圈的转动,还是阻碍了线圈的转动?
电动机转动是时,线圈中产生的感应电动势
总要削弱电源电动势的作用,阻碍线圈的转动.
──反电动势
2.电动机由于机械故障停转,要立即切断电源。
2.一个矩形线圈,在匀强磁场中绕一个固定轴做匀速转动,当线圈处于如图所示位置时,它的: A.磁通量最大,磁通量变化率最大,感应电动势最大
B.磁通量最小,磁通量变化率最大,感应电动势最大
C.磁通量最大,磁通量变化率最小,感应电动势最大
D.磁通量最小,磁通量变化率最小,感应电动势最大
√
如图所示,导线全部为裸导线,半径为r的圆导线处在垂直于圆平面的匀强磁场中,磁感应强度为B,方向如图。一根长度大于2r的直导线MN,以速率V在圆上自左端匀速滑到右端,电路中定值电阻为R,其余电阻忽略不计。在滑动过程中,通过电阻R的电流的平均值为__________;当MN从圆环左端滑到右端的过程中,通过R的电荷量为_________,当MN通过圆环中心O时,通过R的电流为_________.
(πBrv/2R, πBr2/R,2Brv/R)
应用举例
例1、如图所示为穿过某线路的磁通量Φ随
时间t变化的关系图,试根据图说明:
(1)穿过某线路的磁通量Φ何时最大?
何时最小?
(2)Δφ/Δt何时最大?何时最小?
(3)感应电动势E何时最大?何时最小?
Φ
t
O
t1
t2
t3
t4
注意区分几个物理量:
①Φ、Δφ、Δφ/Δt
②E只与Δφ/Δt有关,
而与Φ、Δφ无关。
思考与讨论:
如图所示,长度都是L、质量都为m的两金属杆ab、cd放在水平
放置的足够长的金属导轨MN、EF上,磁感应强度为B的匀强磁
场强度竖直向上,若ab以速度v向右运动,试回答下列问题:
(不计一切摩擦且导轨足够长)
(1)cd杆将向哪儿动?
(2)两金属杆各做什么性质的运动?
(3)从开始运动直到最后,在金属框架上消耗掉的能量有多少
a
b
d
c
N
F
E
M
B
如图,质量为m,电阻为R,边长为l的正方形线圈从一匀强场区域上方高h处自由下落。设磁场的磁感应强度为B,方向如图,试分析:在线圈下边刚进入磁场到上边尚未进入磁场的过程中,线圈有可能做什么运动,并讨论其条件。
h
l
B
例题5
下落h高度,线框速度为:
若此时线框恰匀速进入磁场,应满足:F安=mg
而F安
线框下落的高度应为:
h0
l
B
v
F安
mg
h0
l
B
v
F安
mg
线框作减速运动,且加速度不断减小
h0
l
B
v
F安
mg
线框作加速运动,且加速度不断减小
讨论
v
t
(1)
(2)
(3)
0
引起磁通量变化的原因
1)稳恒磁场中的导体运动 , 或者回路面积
变化、取向变化等 动生电动势
2)导体不动,磁场变化 感生电动势
电动势
+
-
I
: 非静电的电场强度
动生电动势和感生电动势
+ + + + + + +
+ + + + + + +
+ + + + + + +
+ + + + + + +
+ + + + + + +
O
P
一 动生电动势
动生电动势的非静电力场来源 洛伦兹力
-
- -
++
感应电动势
磁通量 m变
动生电动势
磁场不变,回路面积 S 变
感生电动势
回路不动,磁感应强度变
在磁场中,导体棒AB以 v 沿金属导轨向右运动,导体切割磁力线,回路面积发生变化,导体内产生动生电动势。
自由电子所受的洛仑兹力
产生动生电动势的实质是由于运动导体中的电荷在磁场中受洛仑兹力 fL 的结果。
一、动生电动势的起因
电子感应加速器:在涡旋电场作用下,
电子可以被加速到 10 —100 MeV。
铁
芯
线圈
电
束
子
环形
真空室
B
磁场
基本原理
应用感生电场加速电子的电子感应加速器( betatron ) ,是感生电场存在的最重要的例证之一。
实验装置及原理:
在电磁铁的两极之间安置一个环形真空室,当用交变电流励磁电磁铁时,在环形室内就会感生出很强的、同心环状的有旋电场。用电子枪将电子注入环形室,电子在有旋电场的作用下被加速,并在洛仑兹力的作用下,沿圆形轨道运动。
直流电激励电磁铁:
此时环行真空室中只有恒定的磁场,电子在室内只做匀速圆周运动。
交流电激励电磁铁:
当激励电流增加时,真空室中既有磁场又有有旋电场,电子在其中得到加速。磁场变化越快,电子的加速越明显。
