【专项培优】人教版数学八年级上册第11章三角形培优卷(含答案)
文档属性
| 名称 | 【专项培优】人教版数学八年级上册第11章三角形培优卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
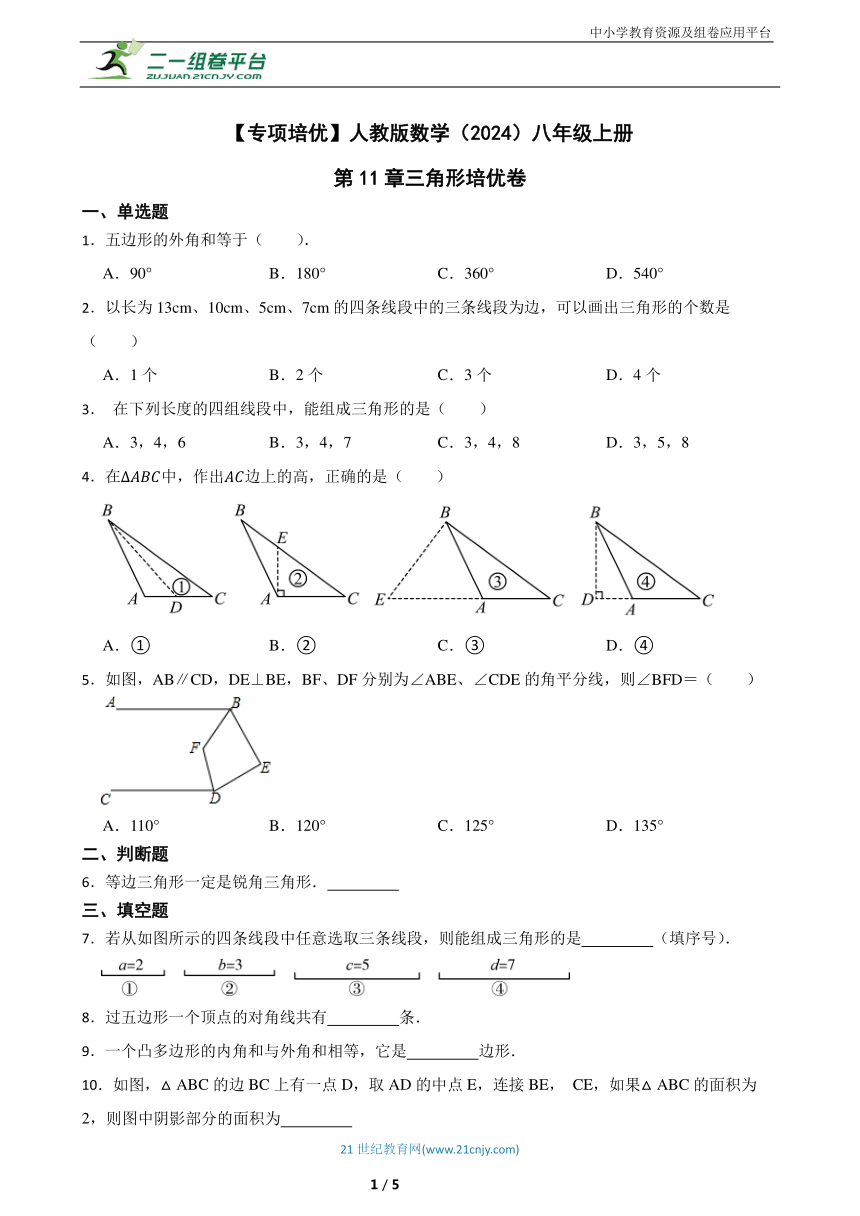
【专项培优】人教版数学(2024)八年级上册
第11章三角形培优卷
一、单选题
1.五边形的外角和等于( ).
A.90° B.180° C.360° D.540°
2.以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
3. 在下列长度的四组线段中,能组成三角形的是( )
A.3,4,6 B.3,4,7 C.3,4,8 D.3,5,8
4.在中,作出边上的高,正确的是( )
A.① B.② C.③ D.④
5.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
二、判断题
6.等边三角形一定是锐角三角形.
三、填空题
7.若从如图所示的四条线段中任意选取三条线段,则能组成三角形的是 (填序号).
8.过五边形一个顶点的对角线共有 条.
9.一个凸多边形的内角和与外角和相等,它是 边形.
10.如图,△ABC的边BC上有一点D,取AD的中点E,连接BE, CE,如果△ABC的面积为2,则图中阴影部分的面积为
11.五边形的内角和的度数是 .
12.如图,小林已经画出了一个三角形的两条角平分线,他说:“我不用再将第三个角平分,就能画出第三条角平分线.”他说的有道理吗 他会怎样做 答: .他这样做的理由是什么 答: .
四、计算题
13.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,求∠BFD的度数.
14.计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
五、解答题
15.如图,是的高,,,求的度数.
六、作图题
16.如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)求△A′B′C′的面积.
七、综合题
17.已知一个三角形的三边长为,若此三角形的周长为偶数,求的值.
18.如图是某款婴儿手推车的平面示意图,若,,,求的度数.
答案解析部分
1.【答案】C
【知识点】多边形内角与外角
2.【答案】C
【知识点】三角形三边关系
3.【答案】A
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形的角平分线、中线和高
5.【答案】D
【知识点】平行线的判定与性质;多边形内角与外角
6.【答案】T
【知识点】三角形相关概念
7.【答案】②③④
【知识点】三角形三边关系
8.【答案】2
【知识点】多边形的对角线
9.【答案】四
【知识点】多边形内角与外角
10.【答案】1
【知识点】三角形的面积
11.【答案】540°
【知识点】多边形内角与外角
12.【答案】有道理;连接CO,并延长交AB于点F,则CF即为∠ACB的平分线;三角形的三条角平分线交于一点
【知识点】三角形的角平分线、中线和高
13.【答案】解:∵AD⊥BC,∠BAD=40°,
∴∠ABD=90°﹣40°=50°.
∵BE是△ABC的内角平分线,
∴∠ABF= ∠ABD=25°,
∴∠BFD=∠BAD+∠ABF=40°+25°=65°.
【知识点】三角形内角和定理
14.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
15.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理
16.【答案】(1)解:如图所示,△A′B′C′即为所求.
(2)解:△A′B′C′的面积为 ×4×4=8.
【知识点】三角形的面积;平移的性质
17.【答案】
【知识点】三角形三边关系
18.【答案】
【知识点】三角形内角和定理;邻补角;内错角的概念
21世纪教育网(www.21cnjy.com)
1 / 1
【专项培优】人教版数学(2024)八年级上册
第11章三角形培优卷
一、单选题
1.五边形的外角和等于( ).
A.90° B.180° C.360° D.540°
2.以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
3. 在下列长度的四组线段中,能组成三角形的是( )
A.3,4,6 B.3,4,7 C.3,4,8 D.3,5,8
4.在中,作出边上的高,正确的是( )
A.① B.② C.③ D.④
5.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
二、判断题
6.等边三角形一定是锐角三角形.
三、填空题
7.若从如图所示的四条线段中任意选取三条线段,则能组成三角形的是 (填序号).
8.过五边形一个顶点的对角线共有 条.
9.一个凸多边形的内角和与外角和相等,它是 边形.
10.如图,△ABC的边BC上有一点D,取AD的中点E,连接BE, CE,如果△ABC的面积为2,则图中阴影部分的面积为
11.五边形的内角和的度数是 .
12.如图,小林已经画出了一个三角形的两条角平分线,他说:“我不用再将第三个角平分,就能画出第三条角平分线.”他说的有道理吗 他会怎样做 答: .他这样做的理由是什么 答: .
四、计算题
13.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,求∠BFD的度数.
14.计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
五、解答题
15.如图,是的高,,,求的度数.
六、作图题
16.如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)求△A′B′C′的面积.
七、综合题
17.已知一个三角形的三边长为,若此三角形的周长为偶数,求的值.
18.如图是某款婴儿手推车的平面示意图,若,,,求的度数.
答案解析部分
1.【答案】C
【知识点】多边形内角与外角
2.【答案】C
【知识点】三角形三边关系
3.【答案】A
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形的角平分线、中线和高
5.【答案】D
【知识点】平行线的判定与性质;多边形内角与外角
6.【答案】T
【知识点】三角形相关概念
7.【答案】②③④
【知识点】三角形三边关系
8.【答案】2
【知识点】多边形的对角线
9.【答案】四
【知识点】多边形内角与外角
10.【答案】1
【知识点】三角形的面积
11.【答案】540°
【知识点】多边形内角与外角
12.【答案】有道理;连接CO,并延长交AB于点F,则CF即为∠ACB的平分线;三角形的三条角平分线交于一点
【知识点】三角形的角平分线、中线和高
13.【答案】解:∵AD⊥BC,∠BAD=40°,
∴∠ABD=90°﹣40°=50°.
∵BE是△ABC的内角平分线,
∴∠ABF= ∠ABD=25°,
∴∠BFD=∠BAD+∠ABF=40°+25°=65°.
【知识点】三角形内角和定理
14.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
15.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理
16.【答案】(1)解:如图所示,△A′B′C′即为所求.
(2)解:△A′B′C′的面积为 ×4×4=8.
【知识点】三角形的面积;平移的性质
17.【答案】
【知识点】三角形三边关系
18.【答案】
【知识点】三角形内角和定理;邻补角;内错角的概念
21世纪教育网(www.21cnjy.com)
1 / 1
