江苏省苏州市昆山市周庄中学2024-2025学年八年级上学期第一次形成性评价数学卷(无答案)
文档属性
| 名称 | 江苏省苏州市昆山市周庄中学2024-2025学年八年级上学期第一次形成性评价数学卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 376.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-04 21:22:09 | ||
图片预览

文档简介
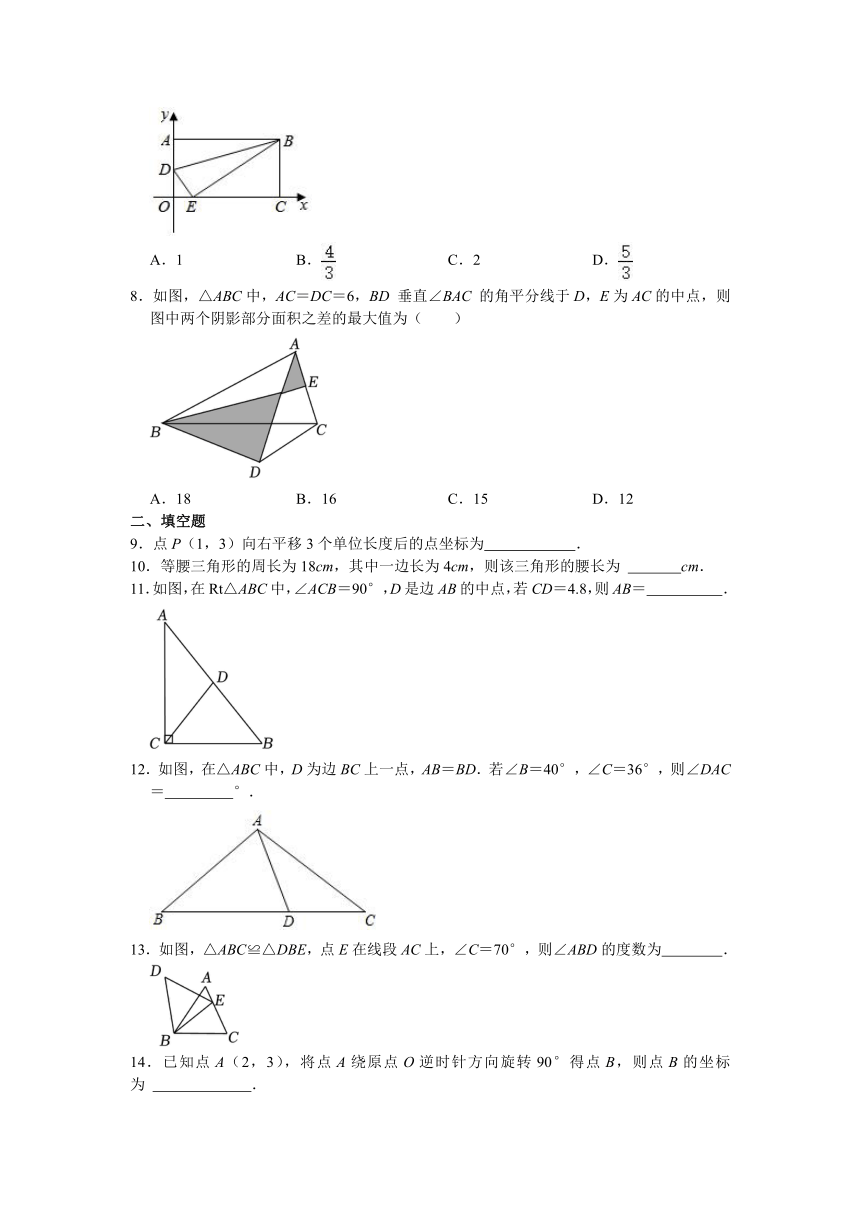
八年级(上)数学第一次形成性评价卷
一、选择题(每题3分)
1.在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.甲、乙、丙三家分别位于△ABC的三个顶点处,现要建造一个超市,使得三家到超市的距离相等,则超市应建造在( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三边垂直平分线的交点
3.如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是( )
A.6 B.8 C.10 D.12
4.已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B'处,DB',EB'分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为( )
A.70° B.75° C.80° D.85°
5.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4 B.6 C.8 D.10
6.已知点A(a﹣1,3),点B(﹣2,a+1),且直线AB∥y轴,则a的值为( )
A.﹣3 B.2 C.1 D.﹣1
7.如图,在平面直角坐标系中,A(0,3),B(5,3),C(5,0),点D在线段OA上,将△ABD沿着直线BD折叠,点A的对应点为E,当点E在线段OC上时,则AD的长是( )
A.1 B. C.2 D.
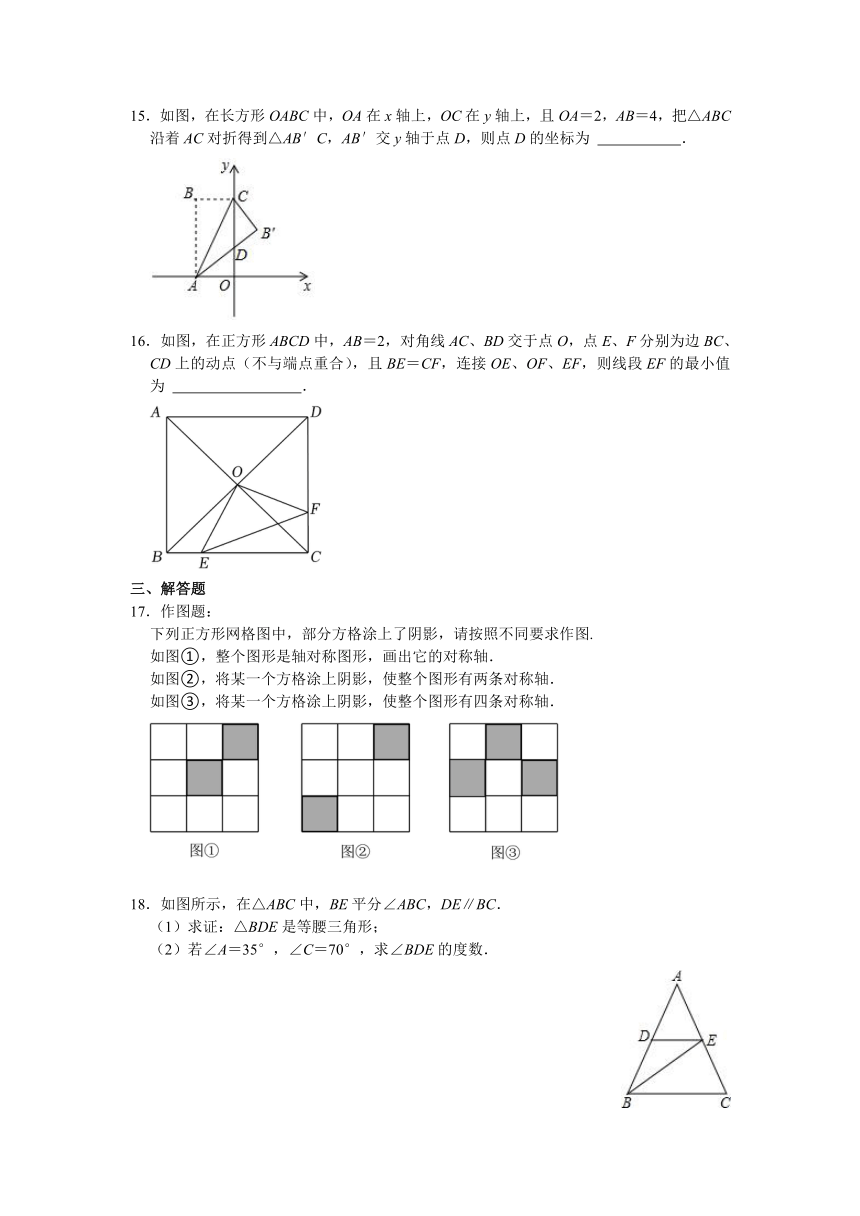
8.如图,△ABC中,AC=DC=6,BD 垂直∠BAC 的角平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为( )
A.18 B.16 C.15 D.12
二、填空题
9.点P(1,3)向右平移3个单位长度后的点坐标为 .
10.等腰三角形的周长为18cm,其中一边长为4cm,则该三角形的腰长为 cm.
11.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,若CD=4.8,则AB= .
12.如图,在△ABC中,D为边BC上一点,AB=BD.若∠B=40°,∠C=36°,则∠DAC= °.
13.如图,△ABC≌△DBE,点E在线段AC上,∠C=70°,则∠ABD的度数为 .
14.已知点A(2,3),将点A绕原点O逆时针方向旋转90°得点B,则点B的坐标为 .
15.如图,在长方形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB′C,AB′交y轴于点D,则点D的坐标为 .
16.如图,在正方形ABCD中,AB=2,对角线AC、BD交于点O,点E、F分别为边BC、CD上的动点(不与端点重合),且BE=CF,连接OE、OF、EF,则线段EF的最小值为 .
三、解答题
17.作图题:
下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
如图①,整个图形是轴对称图形,画出它的对称轴.
如图②,将某一个方格涂上阴影,使整个图形有两条对称轴.
如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
18.如图所示,在△ABC中,BE平分∠ABC,DE∥BC.
(1)求证:△BDE是等腰三角形;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
19.如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE、AC,且AE=AC,求证:
(1)△ABE≌△CDA;
(2)AD∥EC.
20.如图,在Rt△ABC中,∠C=90°,∠B=54°,AD是△ABC的角平分线.
(1)请在AD上确定点E,使得EA=EB;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:DE=DB.
21.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)△ABC和△A1B1C1关于x轴对称,请在坐标系中画出△A1B1C1;
(2)求△ABC的面积;
(3)若P点是x轴上一动点,直接写出PB+PC长度的最小值为 .
22.如图,BD是∠ABC的平分线,AB=BC,点E在BD上,连接AE、CE,过点D作DF⊥AE,DG⊥CE,垂足分别是F、G.
(1)求证:△ABE≌△CBE;
(2)求证:DF=DG.
23.如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)求证:AE=BF;
(2)求DG的长.
24.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
25.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α.
(1)AD、BE相交于点M.
①求证:AD=BE;
②用含α的式子表示∠AMB的度数;
(2)如图2,点P、Q分别是AD、BE的中点,连接CP、CQ,判断△CPQ的形状,并加以证明;
(3)如图3,在△ABC中,∠ACB=45°,BC=,AC=3,以AB为直角边,B为直角顶点作等腰Rt△ABD,则CD= (直接写出结果).
26.如图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(﹣2,0),点C的坐标为(3,0).
(1)求证:△ABC是等腰三角形;
(2)若点P在AO上且点P到∠ACB两边的距离相等,利用尺规作图,找出点P的位置(保留作图痕迹),并求出△ACP的面积;
(3)若动点Q从点O出发,沿着O→A→C的路径运动,当△COQ是等腰三角形时,直接写出点Q的坐标.
一、选择题(每题3分)
1.在平面直角坐标系中,点(3,﹣2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.甲、乙、丙三家分别位于△ABC的三个顶点处,现要建造一个超市,使得三家到超市的距离相等,则超市应建造在( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三边垂直平分线的交点
3.如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是( )
A.6 B.8 C.10 D.12
4.已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B'处,DB',EB'分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为( )
A.70° B.75° C.80° D.85°
5.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4 B.6 C.8 D.10
6.已知点A(a﹣1,3),点B(﹣2,a+1),且直线AB∥y轴,则a的值为( )
A.﹣3 B.2 C.1 D.﹣1
7.如图,在平面直角坐标系中,A(0,3),B(5,3),C(5,0),点D在线段OA上,将△ABD沿着直线BD折叠,点A的对应点为E,当点E在线段OC上时,则AD的长是( )
A.1 B. C.2 D.
8.如图,△ABC中,AC=DC=6,BD 垂直∠BAC 的角平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为( )
A.18 B.16 C.15 D.12
二、填空题
9.点P(1,3)向右平移3个单位长度后的点坐标为 .
10.等腰三角形的周长为18cm,其中一边长为4cm,则该三角形的腰长为 cm.
11.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,若CD=4.8,则AB= .
12.如图,在△ABC中,D为边BC上一点,AB=BD.若∠B=40°,∠C=36°,则∠DAC= °.
13.如图,△ABC≌△DBE,点E在线段AC上,∠C=70°,则∠ABD的度数为 .
14.已知点A(2,3),将点A绕原点O逆时针方向旋转90°得点B,则点B的坐标为 .
15.如图,在长方形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB′C,AB′交y轴于点D,则点D的坐标为 .
16.如图,在正方形ABCD中,AB=2,对角线AC、BD交于点O,点E、F分别为边BC、CD上的动点(不与端点重合),且BE=CF,连接OE、OF、EF,则线段EF的最小值为 .
三、解答题
17.作图题:
下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
如图①,整个图形是轴对称图形,画出它的对称轴.
如图②,将某一个方格涂上阴影,使整个图形有两条对称轴.
如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
18.如图所示,在△ABC中,BE平分∠ABC,DE∥BC.
(1)求证:△BDE是等腰三角形;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
19.如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE、AC,且AE=AC,求证:
(1)△ABE≌△CDA;
(2)AD∥EC.
20.如图,在Rt△ABC中,∠C=90°,∠B=54°,AD是△ABC的角平分线.
(1)请在AD上确定点E,使得EA=EB;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:DE=DB.
21.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)△ABC和△A1B1C1关于x轴对称,请在坐标系中画出△A1B1C1;
(2)求△ABC的面积;
(3)若P点是x轴上一动点,直接写出PB+PC长度的最小值为 .
22.如图,BD是∠ABC的平分线,AB=BC,点E在BD上,连接AE、CE,过点D作DF⊥AE,DG⊥CE,垂足分别是F、G.
(1)求证:△ABE≌△CBE;
(2)求证:DF=DG.
23.如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)求证:AE=BF;
(2)求DG的长.
24.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC=13,CD=5,连接ED,求△EDC的面积.
25.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α.
(1)AD、BE相交于点M.
①求证:AD=BE;
②用含α的式子表示∠AMB的度数;
(2)如图2,点P、Q分别是AD、BE的中点,连接CP、CQ,判断△CPQ的形状,并加以证明;
(3)如图3,在△ABC中,∠ACB=45°,BC=,AC=3,以AB为直角边,B为直角顶点作等腰Rt△ABD,则CD= (直接写出结果).
26.如图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(﹣2,0),点C的坐标为(3,0).
(1)求证:△ABC是等腰三角形;
(2)若点P在AO上且点P到∠ACB两边的距离相等,利用尺规作图,找出点P的位置(保留作图痕迹),并求出△ACP的面积;
(3)若动点Q从点O出发,沿着O→A→C的路径运动,当△COQ是等腰三角形时,直接写出点Q的坐标.
同课章节目录
