九年级上册数学22.3实际问题与二次函数同步练习(含答案)
文档属性
| 名称 | 九年级上册数学22.3实际问题与二次函数同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 530.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-05 00:00:00 | ||
图片预览




文档简介
九年级上册数学 22.3 实际问题与二次函数 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某种商品每天的销售利润元与单价元之间的函数关系式为,则这种商品每天的最大利润为( )
A.50元 B.60元 C.40元 D.30元
2.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为,该药品原价为元,降价后的价格为元,则与的函数关系式为( )
A. B. C. D.
3.用72米木料制作成一个如图所示的“目”形长方形大窗框(横档,也用木料).其中,要使窗框的面积最大,则的长为( )
A.8米 B.9米 C.10米 D.米
4.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
5.多人花样跳绳形式多样、对场地要求低、操作简单、健身效果明显,受到大众的喜爱.如图,绳被甩至最高处时的形状满足抛物线,甩绳的两名同学两手之间的距离,两人甩绳之手距地面的距离均为,则绳的最高点与地面之间的距离为( )
A. B. C. D.
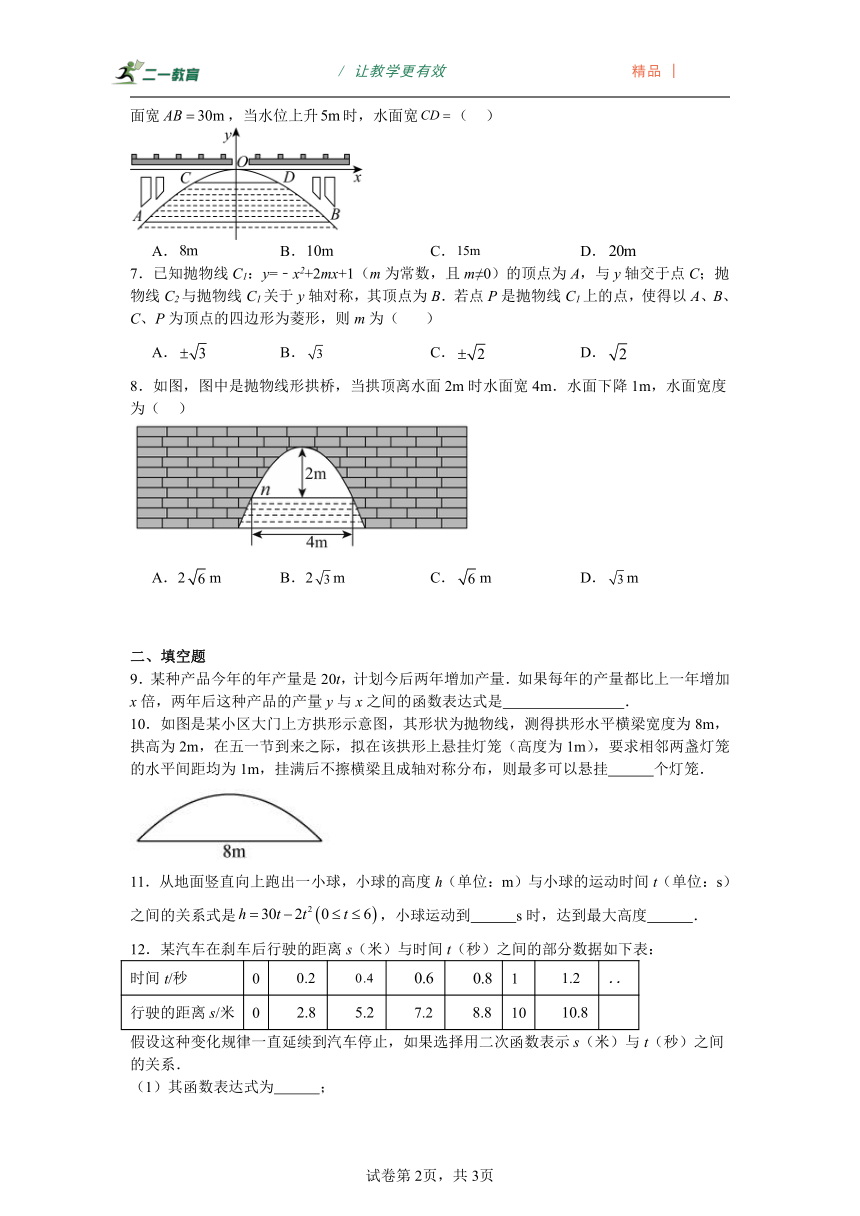
6.如图是根据某拱桥形状建立的直角坐标系,从中得到函数.在正常水位时水面宽,当水位上升时,水面宽( )
A. B. C. D.
7.已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
A. B. C. D.
8.如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( )
A.2m B.2m C.m D.m
二、填空题
9.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .
10.如图是某小区大门上方拱形示意图,其形状为抛物线,测得拱形水平横梁宽度为8m,拱高为2m,在五一节到来之际,拟在该拱形上悬挂灯笼(高度为1m),要求相邻两盏灯笼的水平间距均为1m,挂满后不擦横梁且成轴对称分布,则最多可以悬挂 个灯笼.
11.从地面竖直向上跑出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,小球运动到 s时,达到最大高度 .
12.某汽车在刹车后行驶的距离s(米)与时间t(秒)之间的部分数据如下表:
时间t/秒 0 1 ..
行驶的距离s/米 0 10
假设这种变化规律一直延续到汽车停止,如果选择用二次函数表示s(米)与t(秒)之间的关系.
(1)其函数表达式为 ;
(2)刹车后汽车行驶了 米才停止.
13.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
三、解答题
14.如图,四边形是矩形,,两点在轴的正半轴上,,两点在抛物线,已知,求矩形的周长.
15.某网店经营一种热销的小商品,若该商品的售价为每件元,第天(为正整数)的每件进价为元,与的对应关系如下(为所学过的一次函数或二次函数中的一种):
第天 ……
每件进价(单位:元) ……
(1)直接写出与的函数关系式;
(2)统计发现该网店每天卖掉的件数,设该店每天的利润为元;
①求该店每天利润的最大值;
②若该店每卖一件小商品就捐元给某慈善组织,该店若想在第天获得最大利润,求的取值范围.
16.某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低. 若该果园每棵果树产果(千克),增种果树(棵),它们之间满足函数关系:(且为整数).
(1)求果园的总产量(千克)与增种果树(棵)之间的函数表达式.
(2)当增种果树多少棵时,果园的总产量(千克)最大?最大产量是多少?
17.一位滑雪者从某山坡滑下并滑完全程,滑行距离s(单位:m)与滑行时间t(单位:s)近似满足“一次函数”、“二次函数”或“反比例函数”关系中的一种. 测得一些数据如下:
滑行时间t/s 0 1 2 3 4
滑行距离s/m 0 2 6 12 20
(1)s是t的 函数(填“一次”、“二次”或“反比例”);
(2)求s关于t的函数表达式;
(3)已知第二位滑雪者也从坡顶滑下并滑完全程,且滑行距离与第一位滑雪者相同,滑行距离s(单位:m)与滑行时间t(单位:s)近似满足函数关系.记第一位滑雪者滑完全程所用时间为,第二位滑雪者滑完全程所用时间为,则___(填“<”,“=”或“>”).
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题主要考查了二次函数的实际应用,根据二次函数解析式可知二次函数开口向下,则在对称轴处取得最大值,即60,据此可得答案.
【详解】解:∵某种商品每天的销售利润元与单价元之间的函数关系式为,,
∴当时,y有最大值,最大值为60,
∴这种商品每天的最大利润为60元,
故选B.
2.C
【分析】本题主要考查二次函数的增长率问题.本题需要注意第二次降价是在第一次降价后的价格的基础上降价的.
根据题意可知,原价为,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则即可求得函数关系式.
【详解】解:原价为18,
第一次降价后的价格是,
第二次降价是在第一次降价后的价格的基础上降价的为:,
则函数解析式为:,
故选:C
3.B
【分析】设的长为米,则的长为米.表示出窗框的面积,利用二次函数的性质即可求解.
【详解】解:设的长为米,则的长为米
则窗框的面积
∵
∴当时,窗框的面积最大
故选:B
【点睛】本题考查二次函数的实际应用.掌握建模思想是解题关键.
4.B
【分析】根据售价减去进价表示出实际的利润.
【详解】解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得: 即y=(x-35)(400-5x),
故选:B.
【点睛】本题考查了二次函数的应用,解题的关键是理解“商品每上涨1元,其销售量就减少5个”.
5.C
【分析】本题考查了二次函数的应用,熟练掌握待定系数法是解题关键.先利用待定系数法求出的值,再求出点的坐标,由此即可得.
【详解】解:由题意可知,点的坐标为,
将点代入得:,
解得,
则抛物线的解析式为,
当时,,
所以,
因为两人甩绳之手距地面的距离均为,
所以绳的最高点与地面之间的距离为,
故选:C.
6.D
【分析】本题主要考查了二次函数的实际应用,由题意得,点A的横坐标为,据此求出,进而得到点C的纵坐标为,再求出即可得到答案.
【详解】解:由题意得,点A的横坐标为,
在中,当时,,
∴,
∴点C的纵坐标为,
在中,当时,解得或,
∴,
∴,
故选:D.
7.A
【详解】易知:C(0,1),A(m,m2+1);
若以A、B、C、P为顶点的四边形为菱形,则CP//AB①,CP=AP②;
由①得:点P与点C纵坐标相同,将y=1代入C1,得:x=0或x=2m,即P(2m,1);
由②得:(2m)2=m2+(m2+1﹣1)2,即m2=3,解得m=±;
故选A.
考点:二次函数综合题.
8.A
【详解】建立如图所示直角坐标系:
可设这条抛物线为y=ax2,把点(2,–2)代入,得–2=a×22,解得:a=–,
∴y=–x2,当y=–3时,–x2=–3.解得:x=±,∴水面下降1m,水面宽度为2m.故选A.
9.
【分析】根据每年的产量都比上一年增加x倍,列出函数解析式,即可求解.
【详解】解:根据题意得:
故答案为:
【点睛】本题主要考查了二次函数的实际应用,明确题意,准确得到数量关系是解题的关键.
10.6
【分析】以抛物线状拱形的顶点为原点,建立直角坐标系,即设抛物线的解析式为:,结合图象求出抛物线解析式为:,当时,可得,如图,,问题随之得解.
【详解】如图,以抛物线状拱形的顶点为原点,建立直角坐标系,即设抛物线的解析式为:,
根据题意可知:,
将代入中,有,
解得:,
则抛物线解析式为:,
当时,,解得:,
如图,,
∵相邻两盏灯笼的水平间距均为1m,且按轴对称的方式摆放,
∴共计最多可以挂6盏灯笼,
故答案为:6.
【点睛】本题考查了二次函数的应用,构造合适的直角坐标系,求出二次函数的解析式,是解答本题的关键.
11. 6 108m/108米
【分析】本题考查二次函数的应用,将题目中的函数解析式化为顶点式,即可得到当t为何值时,h取得最大值.
【详解】解:∵,
∴当时,h取得最大值,此时,
故答案为:6,108m.
12.
【分析】本题考查了二次函数的应用,解决问题的关键是熟练掌握二次函数的图像和性质并能结合实际意义比较刹车时的平均速度的大小.
(1)设出二次函数解析式,把3个点的坐标代入可得二次函数解析式,进而再把其余的点代入验证是否在二次函数上;
(2)汽车在刹车时间最长时停止,利用公式法,结合(1)得到的函数解析式,求得相应的最值即可;
【详解】解:(1)设二次函数的解析式为:,
∵抛物线经过点,
,
又由点可得:,
解得:;
∴二次函数的解析式为:;
经检验,其余各点均在上.
(2)解:汽车刹车后到停止时的距离即汽车滑行的最大距离,
当时,滑行距离最大,,
即刹车后汽车行驶了米才停止.
故答案为:;.
13.55
【分析】根据题意,可以得到利润和售价之间的函数关系,然后化为顶点式,即可得到当售价为多少元时,利润达到最大值.
【详解】解:设每顶头盔的售价为x元,获得的利润为w元,
w=(x 40)[200+(60 x)×20]= 20(x 55)2+4500,
∴当x=55时,w取得最大值,此时w=4500.
故答案为:55.
【点睛】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质解答.
14.18
【分析】此题考查了二次函数上点的坐标特点,矩形的性质,解题的关键是求出 C、 D的坐标.
首先将代入求出,得到,然后将代入求出点C的横坐标为5,然后根据矩形的性质求周长即可.
【详解】∵
∴点A的横坐标为1
∴将代入
∴,
∴
∴将代入得,
整理得,
解得或5
∴点C的横坐标为5
∵四边形是矩形
∴,
∴矩形的周长.
15.(1)与的函数关系式为;(2)①当x=11时,该店每天利润的最大值512元;②.
【分析】(1)利用待定系数法代入x与y的对应值得,解方程组即可;
(2)①求出该店每天的利润函数配方得即可;
②该店每天的捐款后利润为,整理得=, 由-2<0,函数图像的开口方向向下,由该店若想在第天获得最大利润,满足不等式组,整理得,解不等式组即可.
【详解】解:(1)∵每天进价差都是0.5常数不变,
∴此函数是一次函数,
设代入x与y的对应值得,
解得,
与的函数关系式为;
(2)①该店每天的利润为,
,
=,
=,
=,
当x=11时,该店每天利润的最大值512元;
②该店每天的利润为,
,
=,
=,
∵-2<0,函数图像的开口方向向下,
∵该店若想在第天获得最大利润,
满足不等式组,
整理得
解得,
解得.
【点睛】本题考查待定系数法求一次函数解析式,二次函数最值的应用,掌握待定系数法求一次函数解析式,二次函数性质是解题关键.
16.(1)
(2)当增种果树棵时,果园的总产量(千克)最大,最大产量是千克
【分析】本题考查了二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的性质解答.
(1)根据总产量每棵果树产果量棵数,即可得到果园的总产量(千克)与增种果树(棵)之间的函数表达式;
(2)根据二次函数的性质即可得出答案.
【详解】(1)解:由题意得:,
果园的总产量(千克)与增种果树(棵)之间的函数表达式为:;
(2)解:,
,抛物线开口向下,
当时,有最大值,此时,
当增种果树棵时,果园的总产量(千克)最大,最大产量是千克.
17.(1)二次
(2)
(3)>
【分析】(1)根据自变量增加1时,函数值依次增加2,4,6,8,可得出结论;
(2)待定系数法求出函数解析式;
(3)时,分别求出,,再比较大小.
【详解】(1)解:根据自变量增加1时,函数值依次增加2,4,6,8,可判断为二次函数,
故答案为:二次.
(2)解:设s关于t的函数表达式为,
根据题意,得
解得
∴s关于t的函数表达式为.
(3)解:根据题意,
当时,,
∴
故答案为>.
【点睛】本题考查了二次函数的应用,根据点的坐标利用待定系数法求出二次函数关系式是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某种商品每天的销售利润元与单价元之间的函数关系式为,则这种商品每天的最大利润为( )
A.50元 B.60元 C.40元 D.30元
2.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为,该药品原价为元,降价后的价格为元,则与的函数关系式为( )
A. B. C. D.
3.用72米木料制作成一个如图所示的“目”形长方形大窗框(横档,也用木料).其中,要使窗框的面积最大,则的长为( )
A.8米 B.9米 C.10米 D.米
4.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是( )
A. B.
C. D.
5.多人花样跳绳形式多样、对场地要求低、操作简单、健身效果明显,受到大众的喜爱.如图,绳被甩至最高处时的形状满足抛物线,甩绳的两名同学两手之间的距离,两人甩绳之手距地面的距离均为,则绳的最高点与地面之间的距离为( )
A. B. C. D.
6.如图是根据某拱桥形状建立的直角坐标系,从中得到函数.在正常水位时水面宽,当水位上升时,水面宽( )
A. B. C. D.
7.已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
A. B. C. D.
8.如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( )
A.2m B.2m C.m D.m
二、填空题
9.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .
10.如图是某小区大门上方拱形示意图,其形状为抛物线,测得拱形水平横梁宽度为8m,拱高为2m,在五一节到来之际,拟在该拱形上悬挂灯笼(高度为1m),要求相邻两盏灯笼的水平间距均为1m,挂满后不擦横梁且成轴对称分布,则最多可以悬挂 个灯笼.
11.从地面竖直向上跑出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,小球运动到 s时,达到最大高度 .
12.某汽车在刹车后行驶的距离s(米)与时间t(秒)之间的部分数据如下表:
时间t/秒 0 1 ..
行驶的距离s/米 0 10
假设这种变化规律一直延续到汽车停止,如果选择用二次函数表示s(米)与t(秒)之间的关系.
(1)其函数表达式为 ;
(2)刹车后汽车行驶了 米才停止.
13.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
三、解答题
14.如图,四边形是矩形,,两点在轴的正半轴上,,两点在抛物线,已知,求矩形的周长.
15.某网店经营一种热销的小商品,若该商品的售价为每件元,第天(为正整数)的每件进价为元,与的对应关系如下(为所学过的一次函数或二次函数中的一种):
第天 ……
每件进价(单位:元) ……
(1)直接写出与的函数关系式;
(2)统计发现该网店每天卖掉的件数,设该店每天的利润为元;
①求该店每天利润的最大值;
②若该店每卖一件小商品就捐元给某慈善组织,该店若想在第天获得最大利润,求的取值范围.
16.某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低. 若该果园每棵果树产果(千克),增种果树(棵),它们之间满足函数关系:(且为整数).
(1)求果园的总产量(千克)与增种果树(棵)之间的函数表达式.
(2)当增种果树多少棵时,果园的总产量(千克)最大?最大产量是多少?
17.一位滑雪者从某山坡滑下并滑完全程,滑行距离s(单位:m)与滑行时间t(单位:s)近似满足“一次函数”、“二次函数”或“反比例函数”关系中的一种. 测得一些数据如下:
滑行时间t/s 0 1 2 3 4
滑行距离s/m 0 2 6 12 20
(1)s是t的 函数(填“一次”、“二次”或“反比例”);
(2)求s关于t的函数表达式;
(3)已知第二位滑雪者也从坡顶滑下并滑完全程,且滑行距离与第一位滑雪者相同,滑行距离s(单位:m)与滑行时间t(单位:s)近似满足函数关系.记第一位滑雪者滑完全程所用时间为,第二位滑雪者滑完全程所用时间为,则___(填“<”,“=”或“>”).
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题主要考查了二次函数的实际应用,根据二次函数解析式可知二次函数开口向下,则在对称轴处取得最大值,即60,据此可得答案.
【详解】解:∵某种商品每天的销售利润元与单价元之间的函数关系式为,,
∴当时,y有最大值,最大值为60,
∴这种商品每天的最大利润为60元,
故选B.
2.C
【分析】本题主要考查二次函数的增长率问题.本题需要注意第二次降价是在第一次降价后的价格的基础上降价的.
根据题意可知,原价为,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则即可求得函数关系式.
【详解】解:原价为18,
第一次降价后的价格是,
第二次降价是在第一次降价后的价格的基础上降价的为:,
则函数解析式为:,
故选:C
3.B
【分析】设的长为米,则的长为米.表示出窗框的面积,利用二次函数的性质即可求解.
【详解】解:设的长为米,则的长为米
则窗框的面积
∵
∴当时,窗框的面积最大
故选:B
【点睛】本题考查二次函数的实际应用.掌握建模思想是解题关键.
4.B
【分析】根据售价减去进价表示出实际的利润.
【详解】解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得: 即y=(x-35)(400-5x),
故选:B.
【点睛】本题考查了二次函数的应用,解题的关键是理解“商品每上涨1元,其销售量就减少5个”.
5.C
【分析】本题考查了二次函数的应用,熟练掌握待定系数法是解题关键.先利用待定系数法求出的值,再求出点的坐标,由此即可得.
【详解】解:由题意可知,点的坐标为,
将点代入得:,
解得,
则抛物线的解析式为,
当时,,
所以,
因为两人甩绳之手距地面的距离均为,
所以绳的最高点与地面之间的距离为,
故选:C.
6.D
【分析】本题主要考查了二次函数的实际应用,由题意得,点A的横坐标为,据此求出,进而得到点C的纵坐标为,再求出即可得到答案.
【详解】解:由题意得,点A的横坐标为,
在中,当时,,
∴,
∴点C的纵坐标为,
在中,当时,解得或,
∴,
∴,
故选:D.
7.A
【详解】易知:C(0,1),A(m,m2+1);
若以A、B、C、P为顶点的四边形为菱形,则CP//AB①,CP=AP②;
由①得:点P与点C纵坐标相同,将y=1代入C1,得:x=0或x=2m,即P(2m,1);
由②得:(2m)2=m2+(m2+1﹣1)2,即m2=3,解得m=±;
故选A.
考点:二次函数综合题.
8.A
【详解】建立如图所示直角坐标系:
可设这条抛物线为y=ax2,把点(2,–2)代入,得–2=a×22,解得:a=–,
∴y=–x2,当y=–3时,–x2=–3.解得:x=±,∴水面下降1m,水面宽度为2m.故选A.
9.
【分析】根据每年的产量都比上一年增加x倍,列出函数解析式,即可求解.
【详解】解:根据题意得:
故答案为:
【点睛】本题主要考查了二次函数的实际应用,明确题意,准确得到数量关系是解题的关键.
10.6
【分析】以抛物线状拱形的顶点为原点,建立直角坐标系,即设抛物线的解析式为:,结合图象求出抛物线解析式为:,当时,可得,如图,,问题随之得解.
【详解】如图,以抛物线状拱形的顶点为原点,建立直角坐标系,即设抛物线的解析式为:,
根据题意可知:,
将代入中,有,
解得:,
则抛物线解析式为:,
当时,,解得:,
如图,,
∵相邻两盏灯笼的水平间距均为1m,且按轴对称的方式摆放,
∴共计最多可以挂6盏灯笼,
故答案为:6.
【点睛】本题考查了二次函数的应用,构造合适的直角坐标系,求出二次函数的解析式,是解答本题的关键.
11. 6 108m/108米
【分析】本题考查二次函数的应用,将题目中的函数解析式化为顶点式,即可得到当t为何值时,h取得最大值.
【详解】解:∵,
∴当时,h取得最大值,此时,
故答案为:6,108m.
12.
【分析】本题考查了二次函数的应用,解决问题的关键是熟练掌握二次函数的图像和性质并能结合实际意义比较刹车时的平均速度的大小.
(1)设出二次函数解析式,把3个点的坐标代入可得二次函数解析式,进而再把其余的点代入验证是否在二次函数上;
(2)汽车在刹车时间最长时停止,利用公式法,结合(1)得到的函数解析式,求得相应的最值即可;
【详解】解:(1)设二次函数的解析式为:,
∵抛物线经过点,
,
又由点可得:,
解得:;
∴二次函数的解析式为:;
经检验,其余各点均在上.
(2)解:汽车刹车后到停止时的距离即汽车滑行的最大距离,
当时,滑行距离最大,,
即刹车后汽车行驶了米才停止.
故答案为:;.
13.55
【分析】根据题意,可以得到利润和售价之间的函数关系,然后化为顶点式,即可得到当售价为多少元时,利润达到最大值.
【详解】解:设每顶头盔的售价为x元,获得的利润为w元,
w=(x 40)[200+(60 x)×20]= 20(x 55)2+4500,
∴当x=55时,w取得最大值,此时w=4500.
故答案为:55.
【点睛】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质解答.
14.18
【分析】此题考查了二次函数上点的坐标特点,矩形的性质,解题的关键是求出 C、 D的坐标.
首先将代入求出,得到,然后将代入求出点C的横坐标为5,然后根据矩形的性质求周长即可.
【详解】∵
∴点A的横坐标为1
∴将代入
∴,
∴
∴将代入得,
整理得,
解得或5
∴点C的横坐标为5
∵四边形是矩形
∴,
∴矩形的周长.
15.(1)与的函数关系式为;(2)①当x=11时,该店每天利润的最大值512元;②.
【分析】(1)利用待定系数法代入x与y的对应值得,解方程组即可;
(2)①求出该店每天的利润函数配方得即可;
②该店每天的捐款后利润为,整理得=, 由-2<0,函数图像的开口方向向下,由该店若想在第天获得最大利润,满足不等式组,整理得,解不等式组即可.
【详解】解:(1)∵每天进价差都是0.5常数不变,
∴此函数是一次函数,
设代入x与y的对应值得,
解得,
与的函数关系式为;
(2)①该店每天的利润为,
,
=,
=,
=,
当x=11时,该店每天利润的最大值512元;
②该店每天的利润为,
,
=,
=,
∵-2<0,函数图像的开口方向向下,
∵该店若想在第天获得最大利润,
满足不等式组,
整理得
解得,
解得.
【点睛】本题考查待定系数法求一次函数解析式,二次函数最值的应用,掌握待定系数法求一次函数解析式,二次函数性质是解题关键.
16.(1)
(2)当增种果树棵时,果园的总产量(千克)最大,最大产量是千克
【分析】本题考查了二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的性质解答.
(1)根据总产量每棵果树产果量棵数,即可得到果园的总产量(千克)与增种果树(棵)之间的函数表达式;
(2)根据二次函数的性质即可得出答案.
【详解】(1)解:由题意得:,
果园的总产量(千克)与增种果树(棵)之间的函数表达式为:;
(2)解:,
,抛物线开口向下,
当时,有最大值,此时,
当增种果树棵时,果园的总产量(千克)最大,最大产量是千克.
17.(1)二次
(2)
(3)>
【分析】(1)根据自变量增加1时,函数值依次增加2,4,6,8,可得出结论;
(2)待定系数法求出函数解析式;
(3)时,分别求出,,再比较大小.
【详解】(1)解:根据自变量增加1时,函数值依次增加2,4,6,8,可判断为二次函数,
故答案为:二次.
(2)解:设s关于t的函数表达式为,
根据题意,得
解得
∴s关于t的函数表达式为.
(3)解:根据题意,
当时,,
∴
故答案为>.
【点睛】本题考查了二次函数的应用,根据点的坐标利用待定系数法求出二次函数关系式是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
