九年级上册数学24.1圆的有关性质同步练习(含解析)
文档属性
| 名称 | 九年级上册数学24.1圆的有关性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-06 00:00:00 | ||
图片预览



文档简介
九年级上册数学 24.1 圆的有关性质 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点在上,,则的度数为( )
A.15° B.30° C.50° D.60°
2.如图,的半径为5,M是弦的中点,且,则的长为( )
A.4 B.6 C.8 D.10
3.如图,的半径为1,内接于,若,,则长为( )
A.2 B. C. D.
4.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(一种水利灌溉工具)的工作原理.如图,筒车盛水桶的运行轨道是以轴心为圆心的圆.已知圆心在水面上方,且被水面截得弦长为米,半径长为米,若点为运行轨道的最低点,则点到弦所在直线的距离是( )
A.米 B.米 C.米 D.米
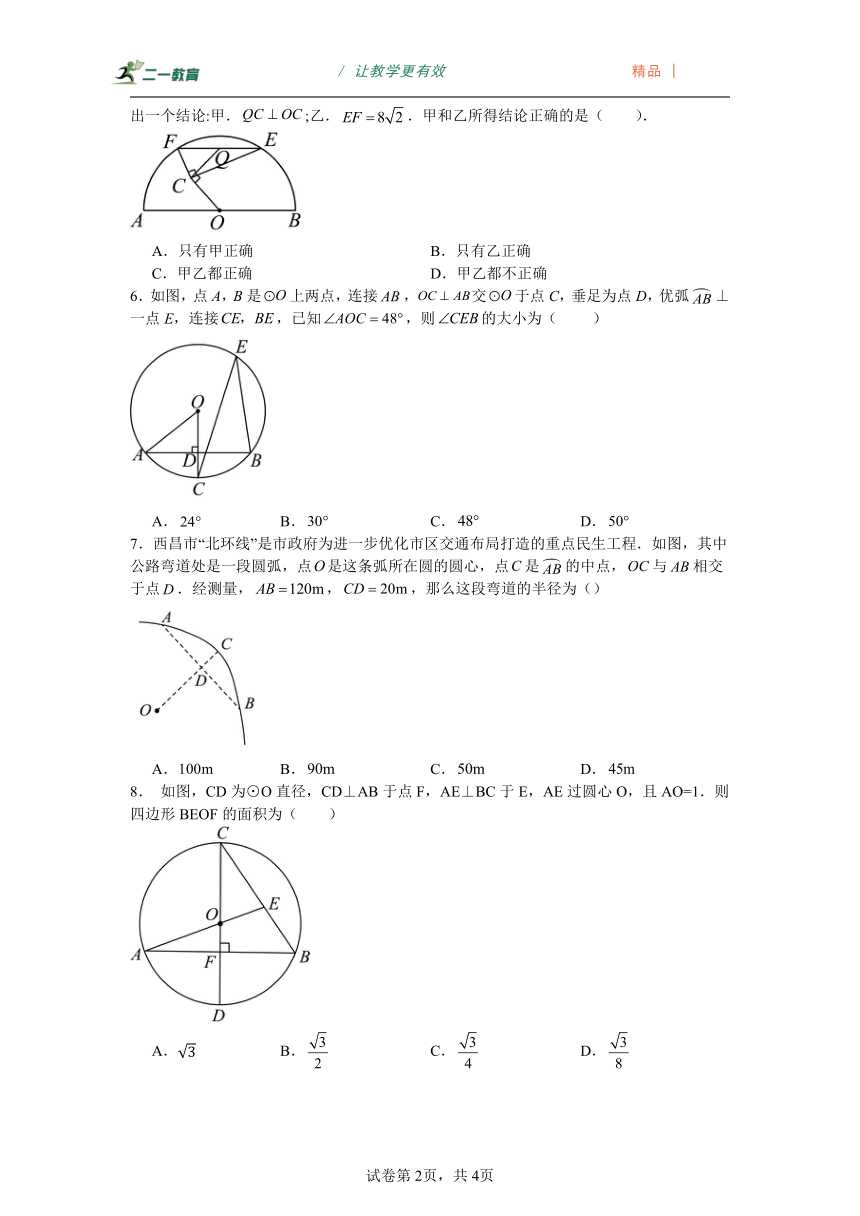
5.如图,AB是半圆的直径,EF为⊙O的弦,为内一点,,,若点为弦的中点,连接QC.甲和乙分别得出一个结论:甲.;乙..甲和乙所得结论正确的是( ).
A.只有甲正确 B.只有乙正确
C.甲乙都正确 D.甲乙都不正确
6.如图,点A,B是上两点,连接,交于点C,垂足为点D,优弧⊥一点E,连接,已知,则的大小为( )
A. B. C. D.
7.西昌市“北环线”是市政府为进一步优化市区交通布局打造的重点民生工程.如图,其中公路弯道处是一段圆弧,点是这条弧所在圆的圆心,点是的中点,与相交于点.经测量,,,那么这段弯道的半径为()
A. B. C. D.
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A. B. C. D.
二、填空题
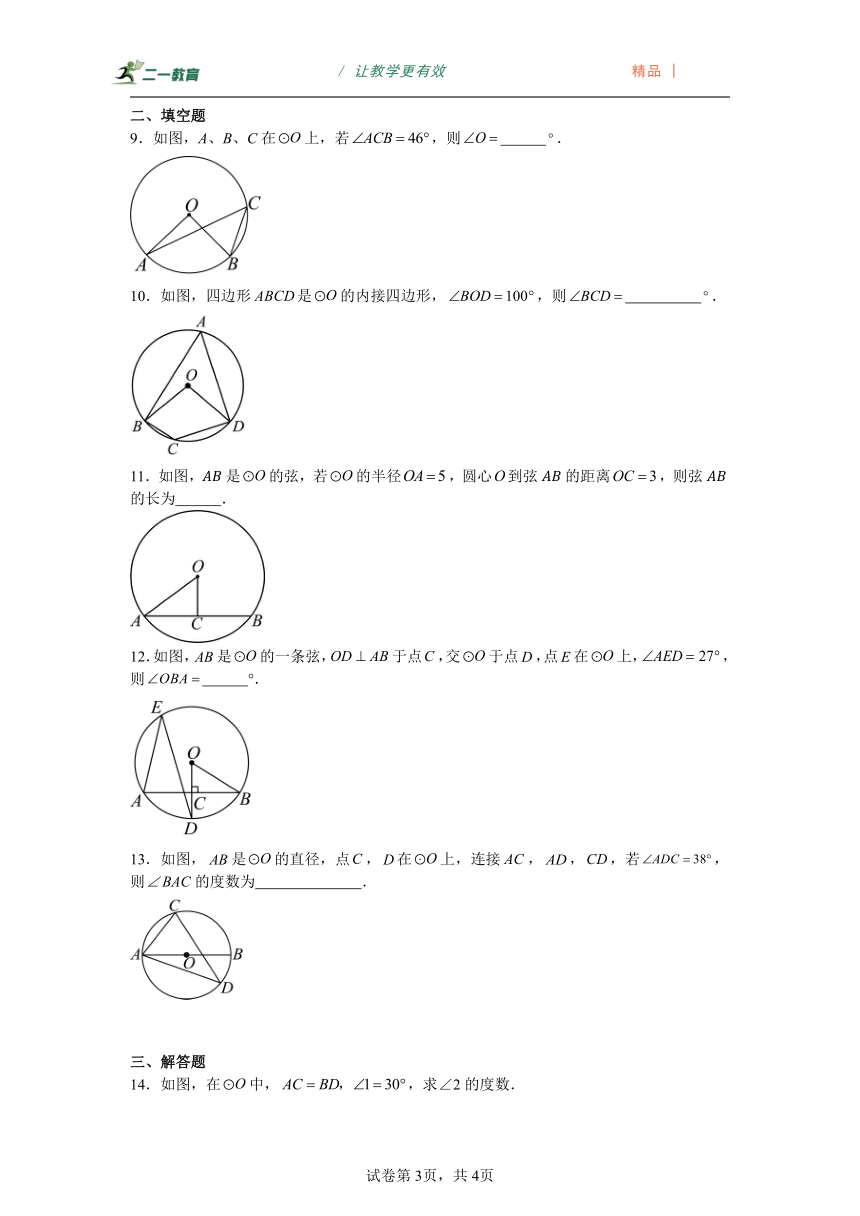
9.如图,A、B、C在上,若,则 .
10.如图,四边形是的内接四边形,,则 .
11.如图,是的弦,若的半径,圆心到弦的距离,则弦的长为 .
12.如图,是的一条弦,于点,交于点,点在上,,则 °.
13.如图,是的直径,点,在上,连接,,,若,则的度数为 .
三、解答题
14.如图,在中,,求∠2的度数.
15.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.经过格点A,B,点C为与格线的交点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)画出该圆的圆心O,并画弦,使平分;
(2)先将弦绕点A顺时针旋转得到线段,再在圆上画点E,使.
16.如图,是的外接圆,平分并交于点,分别连接.
(1)与相等吗?为什么?
(2)若弧的度数与弧的度数之比为,求的度数.
17.如图,为的直径,点C,D为直径同侧圆上的点,且点D为的中点,过点D作于点E,延长,交于点F,与交于点G.
(Ⅰ)如图①,若点C为的中点,求的度数;
(Ⅱ)如图②,若,求的半径.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了圆周角定理.根据圆周角定理即可得出答案.
【详解】解:∵,,
∴.
故选:D.
2.C
【分析】本题考查的是垂径定理及勾股定理,先根据垂径定理:“平分弦的直径平分这条弦,并且平分弦所对的两条弧”得出,,再根据勾股定理求出的长,故可得出结论.
【详解】解:连接
∵是的弦,点是的中点,
∴,
∴,
在中,
∵,,
∴,
∴
故选:C.
3.B
【分析】连接OA、OB,由三角形内角和可得出∠C=45°,再根据圆周角定理可得∠AOB=90°,即△OAB是等腰直角三角形,又圆半径为1,可得出结论.
【详解】解:如图,连接OA、OB,
在△ABC中,∠BAC=60°,∠ABC=75°,
∴∠ACB=180° ∠A ∠B=45°,
∴∠AOB=90°,
∵OA=OB,
∴△OAB是等腰直角三角形,
∴AB=OA=.
故选:B.
【点睛】本题主要考查三角形内角和定理,圆周角定理,等腰直角三角形的性质等内容,作出正确的辅助线是解题关键.
4.C
【分析】本题考查的知识点是垂径定理、勾股定理,解题关键是熟练掌握垂径定理.
连接交于点,根据垂径定理得到米,,再根据勾股定理得到即可得解.
【详解】解:连接交于点,
依题得:米,,米,
设,即,
中,,
即,
解得,
即米,
米,
即点到弦所在直线的距离是米.
故选:.
5.C
【详解】连接,,先证,设,则,,在中由勾股定理得,根据垂径定理及推论得,然后在中勾股定理得据此可得出,因此解出即可得的长.
【解答】解:连接,,
∵是的中点,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
即,
∴,
故甲的说法正确;
设,则,,
在中,,,
由勾股定理得: ,
∵是的中点,点半圆的圆心,
∴,
在中,,,
由勾股定理得:,
∴,
整理得:,
∴(舍去负值),
∴,
故乙的说法正确.
故选:C.
【点睛】此题主要考查了垂径定理及其推论,直角三角形的性质,勾股定理等,熟练掌握垂径定理及其推论,灵活运用勾股定理构造方程是解答此题的关键.
6.A
【分析】本题考查垂径定理及圆周角定理,根据垂径定理可得,由圆周角定理可得即可求解.
【详解】∵交于点C,
∴,
∴,
∵,
∴,
故选:A.
7.A
【分析】本题考查垂径定理,勾股定理,圆心角、弧、弦的关系,关键是作辅助线构造直角三角形,由勾股定理列出关于半径的方程.连接,,设这段弯道的半径为,由圆心角、弧、弦的关系得到,由等腰三角形的性质得到,由垂径定理求出的长,由勾股定理得到,求出即可.
【详解】解:连接,,
设这段弯道的半径为,
是的中点,
,
,
,
,
,
,
,
,
,
这段弯道的半径为.
故选:A
8.C
【分析】根据垂径定理求出AF=BF,CE=BE,,求出∠AOD=2∠C,求出∠AOD=2∠A,求出∠A=30°,解直角三角形求出OF和BF,求出OE、BE、BF,根据三角形的面积公式求出即可.
【详解】解:∵CD为直径,CD⊥AB,
∴,
∴∠AOD=2∠C,
∵CD⊥AB,AE⊥BC,
∴∠AFO=∠CEO=90°,
在△AFO和△CEO中
∴△AFO≌△CEO(AAS),
∴∠C=∠A,
∴∠AOD=2∠A,
∵∠AFO=90°,
∴∠A=30°,
∵AO=1,
∴OF=AO=,AF=OF=,
同理CE=,OE=,
连接OB,
∵CD⊥AB,AE⊥BC,CD、AE过O,
∴由垂径定理得:BF=AF=,BE=CE=,
∴四边形BEOF的面积S=S△BFO+S△BEO=××+=,
故选:C.
【点睛】本题考查了垂径定理,圆周角定理,解直角三角形等知识点,能够综合运用定理进行推理是解此题的关键.
9.
【分析】本题考查圆周角定理,根据同弧所对的圆周角是圆心角的一半,即可得出结果.
【详解】解:∵,
∴;
故答案为:.
10.
【分析】本题考查圆周角定理,圆内接四边形性质,根据圆周角定理求出的度数,再根据圆内接四边形的对角互补,进行求解即可.
【详解】解:∵四边形是的内接四边形,,
∴,
∴,
∴;
故答案为:130.
11.
【分析】本题考查了垂径定理,勾股定理,由可得,,进而利用勾股定理求出即可求解,掌握垂径定理是解题的关键.
【详解】解:∵,
∴,,
∵,,
∴,
∴,
故答案为:.
12.36
【分析】本题考查的是圆周角定理.连接,由圆周角定理可得,再由垂直求出度数,最后根据得到,即可求出的度数.
【详解】解:连接,
,
,
∵,
∴,
∴
,
,
故答案为:36.
13.
【分析】本题主要考查了圆周角定理,熟练掌握圆周角定理是解题关键.先根据圆周角定理可得,,再根据直角三角形的性质求解即可得.
【详解】解:如图,连接,
由圆周角定理得:,,
则,
故答案为:.
14.
【分析】本题主要考查了圆的基本性质,全等三角形的性质与判定,证明得到,即可推出.
【详解】解:∵,
∴,
∴,
∴,
∴.
15.(1)见解析
(2)见解析
【分析】(1)取圆与格线交点E,连接交弦的垂直平分线于点O,O即为圆心;连接,交格线于点P,连接并延长,交于点D,连接,即为作求作;
(2)取点C关于圆心O的对称点N,连接,连接,交格线于点F,过点F作于点H, 则线段即为所求作;取与上方的一条格线交点E,则即为所求作.
【详解】(1)解:如图,取圆与格线交点E,连接交弦的垂直平分线于点O,O即为圆心;连接,交格线于点P,连接并延长,交于点D,连接,即为作求作;
∵,
∴为的直径,
∵为弦,垂直平分,
∴为直径所在直线,
∴O为圆心;
∵,
∴,
∴,
∵O为圆心,
∴,为的中点,
∴,
∴,
∴平分;
(2)解:如图,取点C关于圆心O的对称点N,连接,连接,交格线于点F,过点F作于点H, 则线段即为所求作;取与上方的一条格线交点E,则即为所求作.
∵点C关于圆心O的对称点为N,
∴为直径,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
∵为直径,
∴,,
∴,
∴,
∴.
【点睛】本题考查了网格作图,圆周角定理,垂径定理,三角形全等的判定和性质.熟练掌握圆周角定理及其推论,垂径定理,旋转性质,全等三角形的判定和性质,圆的对称性,是解决问题的关键.
16.(1),理由见解析
(2)
【分析】本题考查圆周角定理,三角形内角和定理.
(1)由角平分线的定义得到,由圆周角的定理得到,,根据三角形内角和定理结合平角的定义得,进而得到,推出,即可得出结论;
(2)由(1)可知,根据,得到是周长的,即可求出,即可解答.
【详解】(1)解:,理由如下:
如图,
平分,
,
,
,
,
,
,
,
,
,
;
(2)解:由(1)知,
弧的度数与弧的度数之比为,即,
是周长的,
弧的度数为,即,
.
17.(Ⅰ);(Ⅱ)
【分析】本题考查了圆周角定理、垂径定理、勾股定理等知识,熟练掌握圆周角定理和垂径定理是解题关键.
(Ⅰ)先求出弧的度数,再根据圆周角定理可得,由此即可得;
(Ⅱ)连接,先求出,从而可得,再根据垂径定理可得,然后设的半径为,则,在中,利用勾股定理求解即可得.
【详解】解:(Ⅰ)∵为的直径,点为的中点,点为的中点,
∴,
∴弧的度数为,
∴,
∵,
∴,
∴;
(Ⅱ)如图,连接,
∵为的直径,,
∴,,
∵,
∴,
∴,
∴,
∴,
设的半径为,则,
∵,
∴,
在中,,即,
解得,
所以的半径为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点在上,,则的度数为( )
A.15° B.30° C.50° D.60°
2.如图,的半径为5,M是弦的中点,且,则的长为( )
A.4 B.6 C.8 D.10
3.如图,的半径为1,内接于,若,,则长为( )
A.2 B. C. D.
4.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(一种水利灌溉工具)的工作原理.如图,筒车盛水桶的运行轨道是以轴心为圆心的圆.已知圆心在水面上方,且被水面截得弦长为米,半径长为米,若点为运行轨道的最低点,则点到弦所在直线的距离是( )
A.米 B.米 C.米 D.米
5.如图,AB是半圆的直径,EF为⊙O的弦,为内一点,,,若点为弦的中点,连接QC.甲和乙分别得出一个结论:甲.;乙..甲和乙所得结论正确的是( ).
A.只有甲正确 B.只有乙正确
C.甲乙都正确 D.甲乙都不正确
6.如图,点A,B是上两点,连接,交于点C,垂足为点D,优弧⊥一点E,连接,已知,则的大小为( )
A. B. C. D.
7.西昌市“北环线”是市政府为进一步优化市区交通布局打造的重点民生工程.如图,其中公路弯道处是一段圆弧,点是这条弧所在圆的圆心,点是的中点,与相交于点.经测量,,,那么这段弯道的半径为()
A. B. C. D.
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A. B. C. D.
二、填空题
9.如图,A、B、C在上,若,则 .
10.如图,四边形是的内接四边形,,则 .
11.如图,是的弦,若的半径,圆心到弦的距离,则弦的长为 .
12.如图,是的一条弦,于点,交于点,点在上,,则 °.
13.如图,是的直径,点,在上,连接,,,若,则的度数为 .
三、解答题
14.如图,在中,,求∠2的度数.
15.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.经过格点A,B,点C为与格线的交点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)画出该圆的圆心O,并画弦,使平分;
(2)先将弦绕点A顺时针旋转得到线段,再在圆上画点E,使.
16.如图,是的外接圆,平分并交于点,分别连接.
(1)与相等吗?为什么?
(2)若弧的度数与弧的度数之比为,求的度数.
17.如图,为的直径,点C,D为直径同侧圆上的点,且点D为的中点,过点D作于点E,延长,交于点F,与交于点G.
(Ⅰ)如图①,若点C为的中点,求的度数;
(Ⅱ)如图②,若,求的半径.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了圆周角定理.根据圆周角定理即可得出答案.
【详解】解:∵,,
∴.
故选:D.
2.C
【分析】本题考查的是垂径定理及勾股定理,先根据垂径定理:“平分弦的直径平分这条弦,并且平分弦所对的两条弧”得出,,再根据勾股定理求出的长,故可得出结论.
【详解】解:连接
∵是的弦,点是的中点,
∴,
∴,
在中,
∵,,
∴,
∴
故选:C.
3.B
【分析】连接OA、OB,由三角形内角和可得出∠C=45°,再根据圆周角定理可得∠AOB=90°,即△OAB是等腰直角三角形,又圆半径为1,可得出结论.
【详解】解:如图,连接OA、OB,
在△ABC中,∠BAC=60°,∠ABC=75°,
∴∠ACB=180° ∠A ∠B=45°,
∴∠AOB=90°,
∵OA=OB,
∴△OAB是等腰直角三角形,
∴AB=OA=.
故选:B.
【点睛】本题主要考查三角形内角和定理,圆周角定理,等腰直角三角形的性质等内容,作出正确的辅助线是解题关键.
4.C
【分析】本题考查的知识点是垂径定理、勾股定理,解题关键是熟练掌握垂径定理.
连接交于点,根据垂径定理得到米,,再根据勾股定理得到即可得解.
【详解】解:连接交于点,
依题得:米,,米,
设,即,
中,,
即,
解得,
即米,
米,
即点到弦所在直线的距离是米.
故选:.
5.C
【详解】连接,,先证,设,则,,在中由勾股定理得,根据垂径定理及推论得,然后在中勾股定理得据此可得出,因此解出即可得的长.
【解答】解:连接,,
∵是的中点,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
即,
∴,
故甲的说法正确;
设,则,,
在中,,,
由勾股定理得: ,
∵是的中点,点半圆的圆心,
∴,
在中,,,
由勾股定理得:,
∴,
整理得:,
∴(舍去负值),
∴,
故乙的说法正确.
故选:C.
【点睛】此题主要考查了垂径定理及其推论,直角三角形的性质,勾股定理等,熟练掌握垂径定理及其推论,灵活运用勾股定理构造方程是解答此题的关键.
6.A
【分析】本题考查垂径定理及圆周角定理,根据垂径定理可得,由圆周角定理可得即可求解.
【详解】∵交于点C,
∴,
∴,
∵,
∴,
故选:A.
7.A
【分析】本题考查垂径定理,勾股定理,圆心角、弧、弦的关系,关键是作辅助线构造直角三角形,由勾股定理列出关于半径的方程.连接,,设这段弯道的半径为,由圆心角、弧、弦的关系得到,由等腰三角形的性质得到,由垂径定理求出的长,由勾股定理得到,求出即可.
【详解】解:连接,,
设这段弯道的半径为,
是的中点,
,
,
,
,
,
,
,
,
,
这段弯道的半径为.
故选:A
8.C
【分析】根据垂径定理求出AF=BF,CE=BE,,求出∠AOD=2∠C,求出∠AOD=2∠A,求出∠A=30°,解直角三角形求出OF和BF,求出OE、BE、BF,根据三角形的面积公式求出即可.
【详解】解:∵CD为直径,CD⊥AB,
∴,
∴∠AOD=2∠C,
∵CD⊥AB,AE⊥BC,
∴∠AFO=∠CEO=90°,
在△AFO和△CEO中
∴△AFO≌△CEO(AAS),
∴∠C=∠A,
∴∠AOD=2∠A,
∵∠AFO=90°,
∴∠A=30°,
∵AO=1,
∴OF=AO=,AF=OF=,
同理CE=,OE=,
连接OB,
∵CD⊥AB,AE⊥BC,CD、AE过O,
∴由垂径定理得:BF=AF=,BE=CE=,
∴四边形BEOF的面积S=S△BFO+S△BEO=××+=,
故选:C.
【点睛】本题考查了垂径定理,圆周角定理,解直角三角形等知识点,能够综合运用定理进行推理是解此题的关键.
9.
【分析】本题考查圆周角定理,根据同弧所对的圆周角是圆心角的一半,即可得出结果.
【详解】解:∵,
∴;
故答案为:.
10.
【分析】本题考查圆周角定理,圆内接四边形性质,根据圆周角定理求出的度数,再根据圆内接四边形的对角互补,进行求解即可.
【详解】解:∵四边形是的内接四边形,,
∴,
∴,
∴;
故答案为:130.
11.
【分析】本题考查了垂径定理,勾股定理,由可得,,进而利用勾股定理求出即可求解,掌握垂径定理是解题的关键.
【详解】解:∵,
∴,,
∵,,
∴,
∴,
故答案为:.
12.36
【分析】本题考查的是圆周角定理.连接,由圆周角定理可得,再由垂直求出度数,最后根据得到,即可求出的度数.
【详解】解:连接,
,
,
∵,
∴,
∴
,
,
故答案为:36.
13.
【分析】本题主要考查了圆周角定理,熟练掌握圆周角定理是解题关键.先根据圆周角定理可得,,再根据直角三角形的性质求解即可得.
【详解】解:如图,连接,
由圆周角定理得:,,
则,
故答案为:.
14.
【分析】本题主要考查了圆的基本性质,全等三角形的性质与判定,证明得到,即可推出.
【详解】解:∵,
∴,
∴,
∴,
∴.
15.(1)见解析
(2)见解析
【分析】(1)取圆与格线交点E,连接交弦的垂直平分线于点O,O即为圆心;连接,交格线于点P,连接并延长,交于点D,连接,即为作求作;
(2)取点C关于圆心O的对称点N,连接,连接,交格线于点F,过点F作于点H, 则线段即为所求作;取与上方的一条格线交点E,则即为所求作.
【详解】(1)解:如图,取圆与格线交点E,连接交弦的垂直平分线于点O,O即为圆心;连接,交格线于点P,连接并延长,交于点D,连接,即为作求作;
∵,
∴为的直径,
∵为弦,垂直平分,
∴为直径所在直线,
∴O为圆心;
∵,
∴,
∴,
∵O为圆心,
∴,为的中点,
∴,
∴,
∴平分;
(2)解:如图,取点C关于圆心O的对称点N,连接,连接,交格线于点F,过点F作于点H, 则线段即为所求作;取与上方的一条格线交点E,则即为所求作.
∵点C关于圆心O的对称点为N,
∴为直径,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
∵为直径,
∴,,
∴,
∴,
∴.
【点睛】本题考查了网格作图,圆周角定理,垂径定理,三角形全等的判定和性质.熟练掌握圆周角定理及其推论,垂径定理,旋转性质,全等三角形的判定和性质,圆的对称性,是解决问题的关键.
16.(1),理由见解析
(2)
【分析】本题考查圆周角定理,三角形内角和定理.
(1)由角平分线的定义得到,由圆周角的定理得到,,根据三角形内角和定理结合平角的定义得,进而得到,推出,即可得出结论;
(2)由(1)可知,根据,得到是周长的,即可求出,即可解答.
【详解】(1)解:,理由如下:
如图,
平分,
,
,
,
,
,
,
,
,
,
;
(2)解:由(1)知,
弧的度数与弧的度数之比为,即,
是周长的,
弧的度数为,即,
.
17.(Ⅰ);(Ⅱ)
【分析】本题考查了圆周角定理、垂径定理、勾股定理等知识,熟练掌握圆周角定理和垂径定理是解题关键.
(Ⅰ)先求出弧的度数,再根据圆周角定理可得,由此即可得;
(Ⅱ)连接,先求出,从而可得,再根据垂径定理可得,然后设的半径为,则,在中,利用勾股定理求解即可得.
【详解】解:(Ⅰ)∵为的直径,点为的中点,点为的中点,
∴,
∴弧的度数为,
∴,
∵,
∴,
∴;
(Ⅱ)如图,连接,
∵为的直径,,
∴,,
∵,
∴,
∴,
∴,
∴,
设的半径为,则,
∵,
∴,
在中,,即,
解得,
所以的半径为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
