北师大版八年级上册探索勾股定理说课课件
文档属性
| 名称 | 北师大版八年级上册探索勾股定理说课课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 493.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-20 00:00:00 | ||
图片预览







文档简介
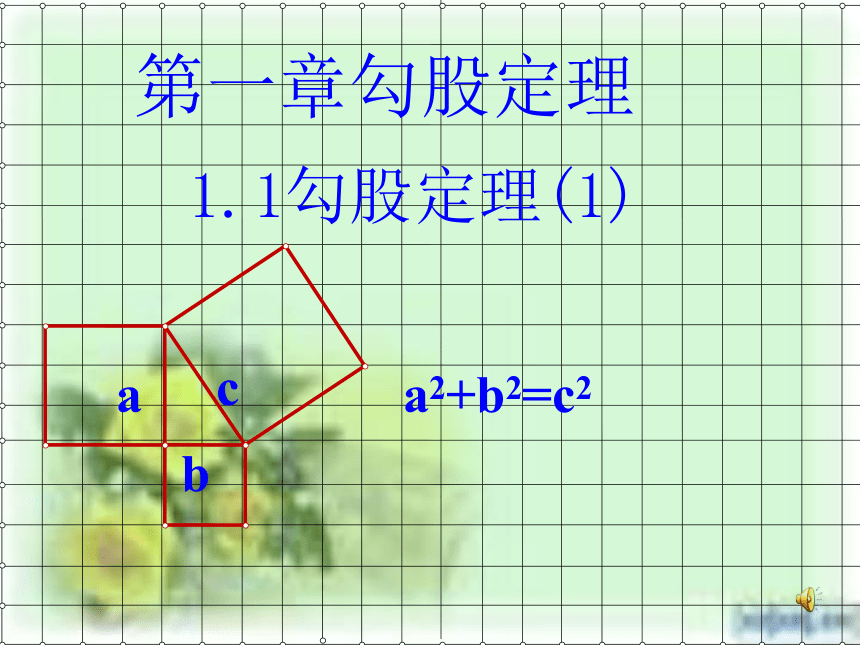
课件23张PPT。第一章勾股定理baca2+b2=c21.1勾股定理(1)一、教材分析三、学法指导二、教法分析四、教学过程
(一)教材的地位
这节课是九年制义务教育初级中学教材北师大版八年级第一章第1节《探索勾股定理》第一课时,勾股定理是几何中几个重要定理之一,它揭示的是直角三角形中三边的数量关系。它在数学的发展中起过重要的作用,在现时世界中也有着广泛的作用。
(二)教学三维目标
1、经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
3、 在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法。
4、 通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
(三)教学重点、难点
重点:了解勾股定理的由来,并能用它来解决一些简单的问题。
难点:用面积法(拼图法)发现勾股定理。
一、教材分析返回二、教法分析:
针对八年级学生的知识结构和心理特征,本节课可选择引导探索法,由浅入深,由特殊到一般地提出问题。引导学生自主探索,合作交流,这种教学理念反映了时代精神,有利于提高学生的思维能力,能有效地激发学生的思维积极性,基本教学流程是:提出问题—实验操作—归纳验证—问题解决—课堂小结—布置作业六部分。返回三、学法指导:
在教师的组织引导下,采用自主探索、合作交流的研讨式学习方式,让学生思考问题,获取知识,掌握方法,借此培养学生动手、动脑、动口的能力,使学生真正成为学习的主体。
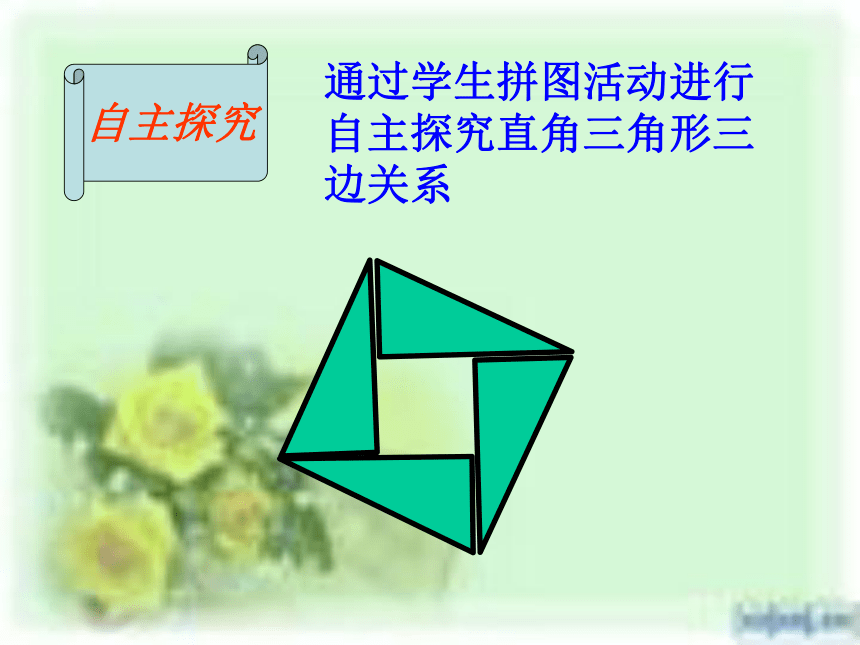
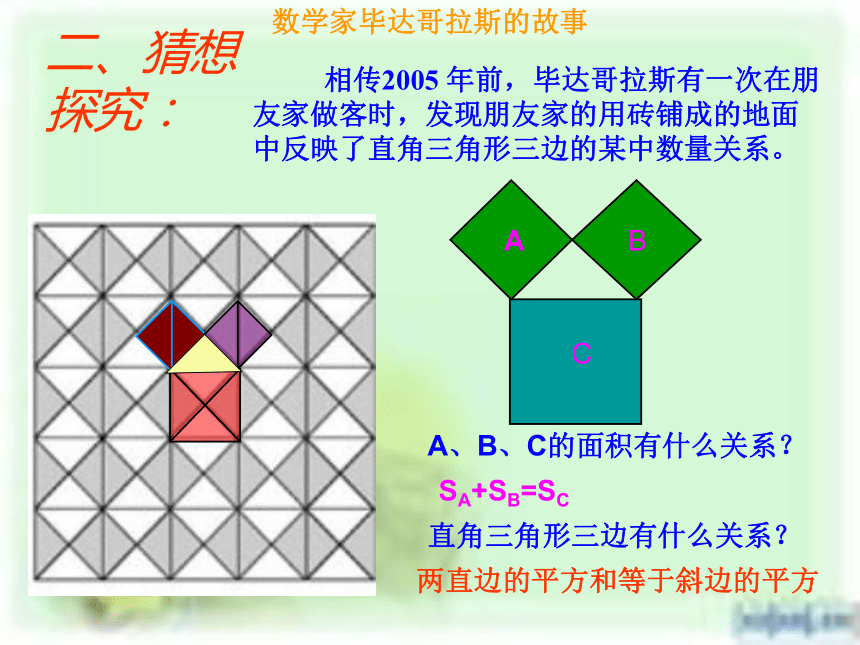
返回1、 情境引入 2、 猜想探究3 、理论证明4、 拓展练习四、教学过程5、 课堂小结6、 布置作业 下图是2002年在北京召开的国 际数学家大会会徽,你知道该图形具有什么特点吗?思考?自主探究通过学生拼图活动进行自主探究直角三角形三边关系 数学家毕达哥拉斯的故事A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方二、猜想探究: 相传2005 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某中数量关系。图1—1444488A的面积+ B的面积= C的面积图1—299991818A的面积+ B的面积= C的面积边为特殊值的直角三角形有下列性质:
对于任意直角三角形都有这样的性质吗?两直边的平方和等于斜边的平方看下图大胆尝试,练一练!图1-3图1-4491392534sA+sB=sC两直角边的平方和
等于斜边的平方探究二:你会求出三角形的面积吗?cb ? a c2 = (a ? b)2 + 4(?ab)
= a2 ? 2ab + b2 + 2ab
? c2 = a2 + b2问题一 你能证明下列图形吗? 讨论分析解题思路赵爽弦图三、 理论证明 在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么,只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。问题二 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟∟∟ba (a + b)2 = c2 + 4(?ab)
a2 + 2ab + b2 = c2 + 2ab
? a2 + b2 = c2c问题三 目前,世界上共有500多种证明“勾股定理”的方法。 定理: 经过证明被确认是正确的命题叫做定理。勾股弦1 错例辩析
(1)三角形ABC的两边为3和4,求第三边
解:由于三角形的两边为3和4
所以它的第三边C=5
(2)若告诉三角形ABC是直角三角形,第三边也不一定是满足,题目中并未交待C是斜边
综合上述这个题目条件不足,第三边无法求得,进一步体会勾股定理的前提——直角三角形
2 课堂练习
做本节前问题 :求折断之前旗杆有多高?
合作交流 试一试四1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。感悟与反思:五作业:1.完成课本习题1.1 1, 2, 3, 4。
2.收集有关勾股定理的事例。六、谢谢合作!
(一)教材的地位
这节课是九年制义务教育初级中学教材北师大版八年级第一章第1节《探索勾股定理》第一课时,勾股定理是几何中几个重要定理之一,它揭示的是直角三角形中三边的数量关系。它在数学的发展中起过重要的作用,在现时世界中也有着广泛的作用。
(二)教学三维目标
1、经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
3、 在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法。
4、 通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
(三)教学重点、难点
重点:了解勾股定理的由来,并能用它来解决一些简单的问题。
难点:用面积法(拼图法)发现勾股定理。
一、教材分析返回二、教法分析:
针对八年级学生的知识结构和心理特征,本节课可选择引导探索法,由浅入深,由特殊到一般地提出问题。引导学生自主探索,合作交流,这种教学理念反映了时代精神,有利于提高学生的思维能力,能有效地激发学生的思维积极性,基本教学流程是:提出问题—实验操作—归纳验证—问题解决—课堂小结—布置作业六部分。返回三、学法指导:
在教师的组织引导下,采用自主探索、合作交流的研讨式学习方式,让学生思考问题,获取知识,掌握方法,借此培养学生动手、动脑、动口的能力,使学生真正成为学习的主体。
返回1、 情境引入 2、 猜想探究3 、理论证明4、 拓展练习四、教学过程5、 课堂小结6、 布置作业 下图是2002年在北京召开的国 际数学家大会会徽,你知道该图形具有什么特点吗?思考?自主探究通过学生拼图活动进行自主探究直角三角形三边关系 数学家毕达哥拉斯的故事A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方二、猜想探究: 相传2005 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某中数量关系。图1—1444488A的面积+ B的面积= C的面积图1—299991818A的面积+ B的面积= C的面积边为特殊值的直角三角形有下列性质:
对于任意直角三角形都有这样的性质吗?两直边的平方和等于斜边的平方看下图大胆尝试,练一练!图1-3图1-4491392534sA+sB=sC两直角边的平方和
等于斜边的平方探究二:你会求出三角形的面积吗?cb ? a c2 = (a ? b)2 + 4(?ab)
= a2 ? 2ab + b2 + 2ab
? c2 = a2 + b2问题一 你能证明下列图形吗? 讨论分析解题思路赵爽弦图三、 理论证明 在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么,只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。问题二 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟∟∟ba (a + b)2 = c2 + 4(?ab)
a2 + 2ab + b2 = c2 + 2ab
? a2 + b2 = c2c问题三 目前,世界上共有500多种证明“勾股定理”的方法。 定理: 经过证明被确认是正确的命题叫做定理。勾股弦1 错例辩析
(1)三角形ABC的两边为3和4,求第三边
解:由于三角形的两边为3和4
所以它的第三边C=5
(2)若告诉三角形ABC是直角三角形,第三边也不一定是满足,题目中并未交待C是斜边
综合上述这个题目条件不足,第三边无法求得,进一步体会勾股定理的前提——直角三角形
2 课堂练习
做本节前问题 :求折断之前旗杆有多高?
合作交流 试一试四1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。感悟与反思:五作业:1.完成课本习题1.1 1, 2, 3, 4。
2.收集有关勾股定理的事例。六、谢谢合作!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
