湘教版数学八年级下册(新) 课件:1.1.1直角三角形的性质和判定(共14张PPT)
文档属性
| 名称 | 湘教版数学八年级下册(新) 课件:1.1.1直角三角形的性质和判定(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-14 16:51:32 | ||
图片预览


文档简介
课件14张PPT。直角三角形性质和判定(1)
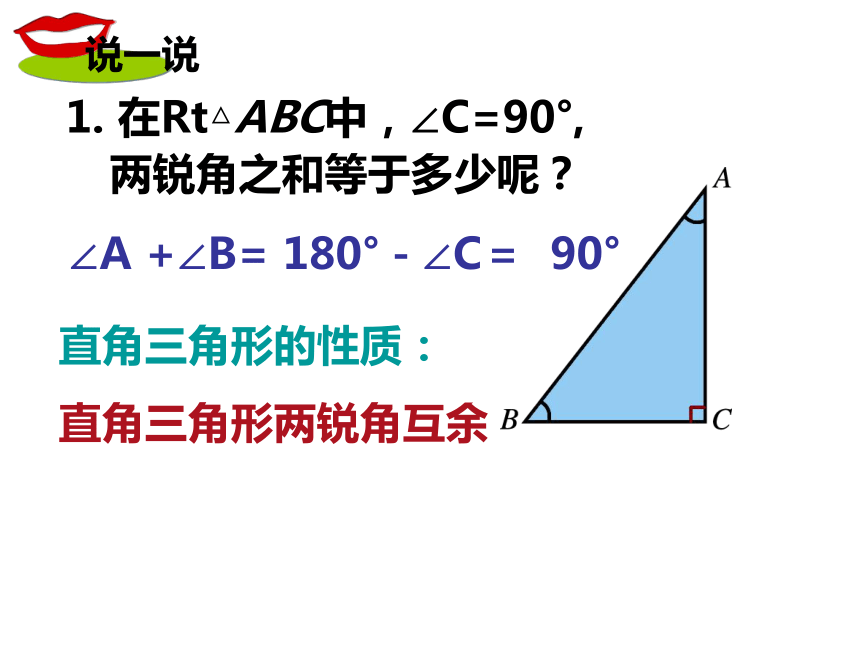
1.1 1. 在Rt△ABC中,∠C=90°,
两锐角之和等于多少呢?∠A +∠B= 180°-∠C= 90°直角三角形的性质:
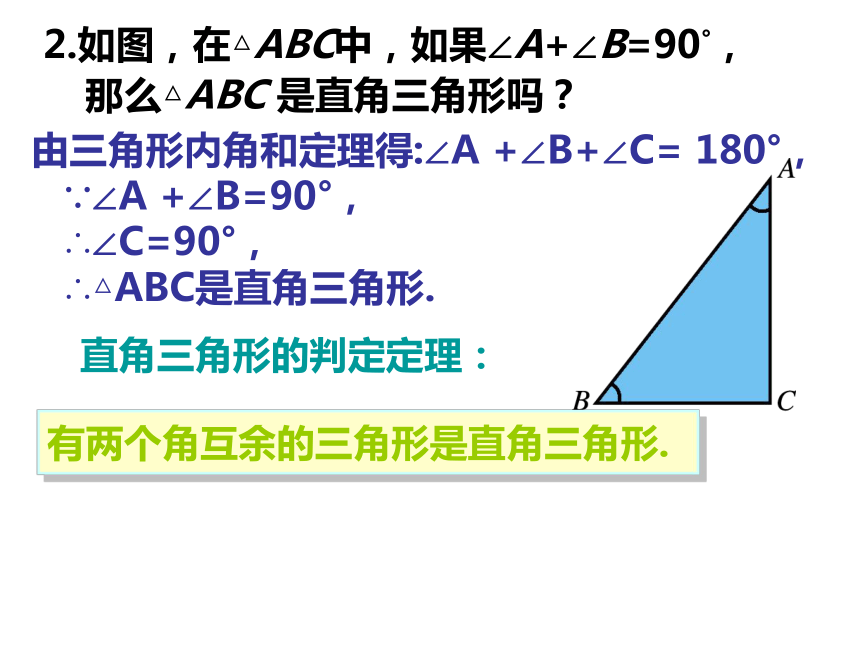
直角三角形两锐角互余 2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC 是直角三角形吗? 由三角形内角和定理得:∠A +∠B+∠C= 180°,
∵∠A +∠B=90°,
∴∠C=90°,
∴△ABC是直角三角形.
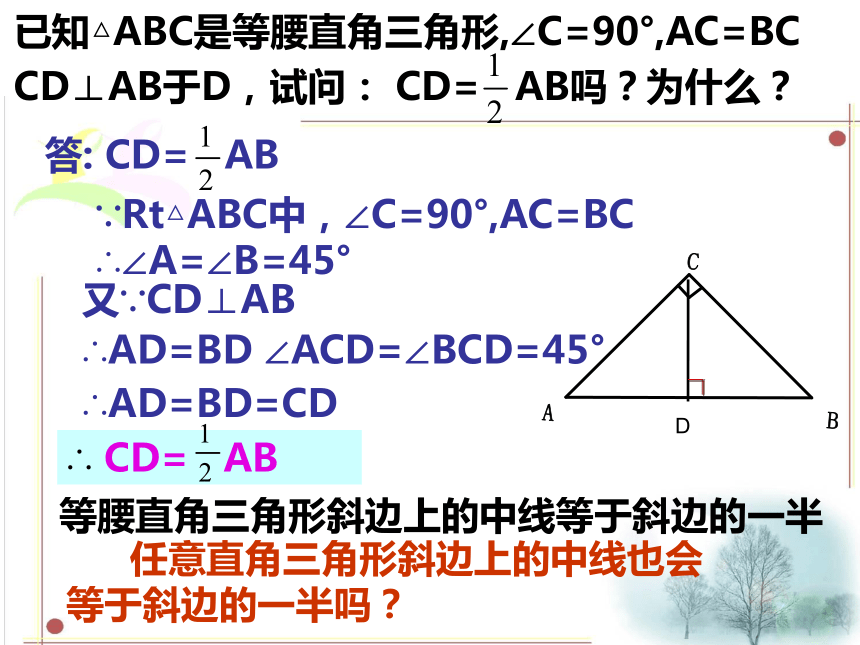
有两个角互余的三角形是直角三角形. 直角三角形的判定定理:已知△ABC是等腰直角三角形,∠C=90°,AC=BC CD⊥AB于D,试问: CD= AB吗?为什么? ∵Rt△ABC中,∠C=90°,AC=BC ∴∠A=∠B=45°D又∵CD⊥AB
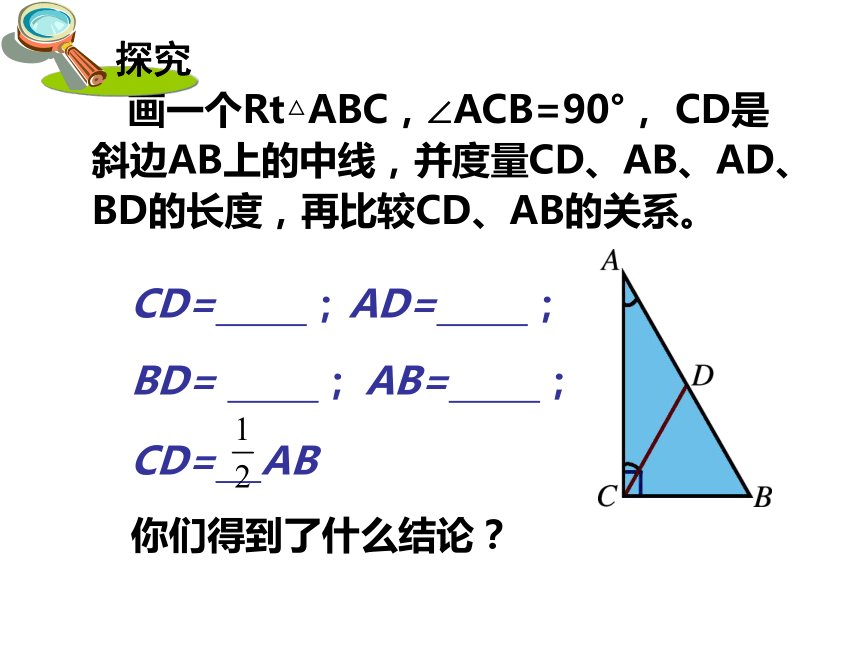
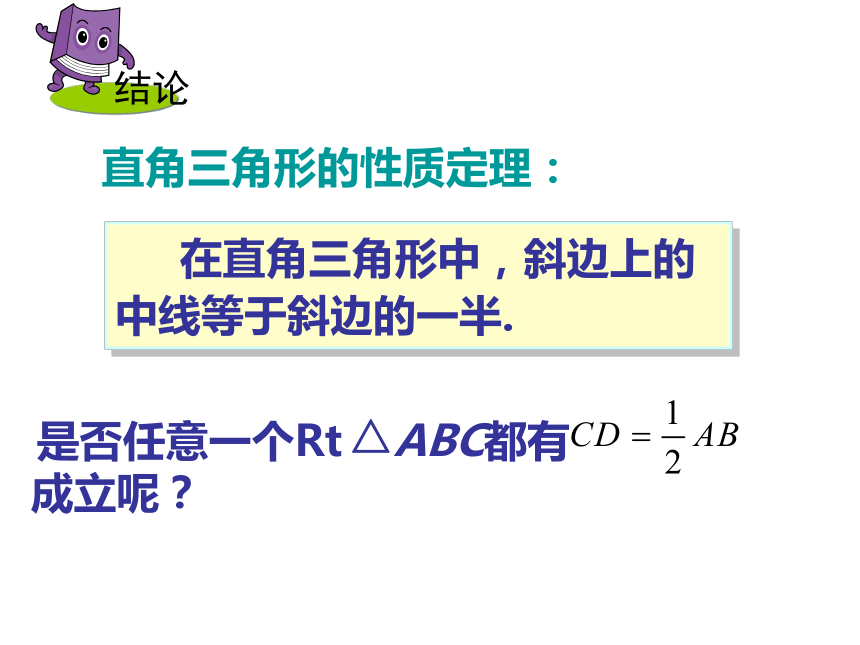
∴AD=BD ∠ACD=∠BCD=45°∴ CD= AB 任意直角三角形斜边上的中线也会等于斜边的一半吗?等腰直角三角形斜边上的中线等于斜边的一半答: CD= AB∴AD=BD=CD 画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。CD= ;AD= ;BD= ;AB= ;CD= AB你们得到了什么结论? 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理: 是否任意一个Rt ABC都有 成立呢?
△图2 如图1,如果中线 ,即CD=AD,
所以∠ACD=∠A。于是在图2中,过
Rt ABC 的直角顶点 C 作射线 CD′交 AB
于D′,使 ∠1 = ∠A,则有
(等角对等边)图1AD′=CD′.△直角三角形两锐角互余又∵∠A+∠B=90° ( )
∠1+∠2=90° ∴ ∠B =∠2 (等角对等边)∴∴ D′是斜边AB的中点 即CD′就是斜边AB的中线,从而 CD′与CD重合,并且有例题:如图,已知CD是△ABC的
AB边上的中线,且CD= AB
求证: △ABC是直角三角形证明∵∴ ∠1=∠A等边对等角∠2=∠B ( )又 ∵ ∠A+∠B+∠ACB =180°
(三角形内角和的性质)即∠A+∠B+∠1+∠2=180°∴ 2(∠A+∠B)=180°∴ ∠A+∠B =90°∴ △ABC是直角三角形( ) 有两个角互余的三角形是
直角三角形 三角形一边上的中线等于这条边的一半的三角形是直角三角形. 直角三角形的判定定理:(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????; (2)在Rt△ABC中,∠C=90度,∠A -∠B =30°,那么∠A=?????? ,∠B=?????? ;(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.(4)在直角三角形中,斜边及其中线之和
为6,那么该三角形的斜边长为________. 本节课我们学习了哪些内容?1:直角三角形两锐角互余;2:在直角三角形中,斜边上的中线等于斜边的一半;
……2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。3:有两个角互余的三角形是直角三角形; ……1、如图,在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的高,那么,
与∠B互余的角有????????,
与∠A互余的角有????????,
与∠B相等的角有????????? ,
与∠A相等的角有?????????.作业:
1.1 1. 在Rt△ABC中,∠C=90°,
两锐角之和等于多少呢?∠A +∠B= 180°-∠C= 90°直角三角形的性质:
直角三角形两锐角互余 2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC 是直角三角形吗? 由三角形内角和定理得:∠A +∠B+∠C= 180°,
∵∠A +∠B=90°,
∴∠C=90°,
∴△ABC是直角三角形.
有两个角互余的三角形是直角三角形. 直角三角形的判定定理:已知△ABC是等腰直角三角形,∠C=90°,AC=BC CD⊥AB于D,试问: CD= AB吗?为什么? ∵Rt△ABC中,∠C=90°,AC=BC ∴∠A=∠B=45°D又∵CD⊥AB
∴AD=BD ∠ACD=∠BCD=45°∴ CD= AB 任意直角三角形斜边上的中线也会等于斜边的一半吗?等腰直角三角形斜边上的中线等于斜边的一半答: CD= AB∴AD=BD=CD 画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。CD= ;AD= ;BD= ;AB= ;CD= AB你们得到了什么结论? 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理: 是否任意一个Rt ABC都有 成立呢?
△图2 如图1,如果中线 ,即CD=AD,
所以∠ACD=∠A。于是在图2中,过
Rt ABC 的直角顶点 C 作射线 CD′交 AB
于D′,使 ∠1 = ∠A,则有
(等角对等边)图1AD′=CD′.△直角三角形两锐角互余又∵∠A+∠B=90° ( )
∠1+∠2=90° ∴ ∠B =∠2 (等角对等边)∴∴ D′是斜边AB的中点 即CD′就是斜边AB的中线,从而 CD′与CD重合,并且有例题:如图,已知CD是△ABC的
AB边上的中线,且CD= AB
求证: △ABC是直角三角形证明∵∴ ∠1=∠A等边对等角∠2=∠B ( )又 ∵ ∠A+∠B+∠ACB =180°
(三角形内角和的性质)即∠A+∠B+∠1+∠2=180°∴ 2(∠A+∠B)=180°∴ ∠A+∠B =90°∴ △ABC是直角三角形( ) 有两个角互余的三角形是
直角三角形 三角形一边上的中线等于这条边的一半的三角形是直角三角形. 直角三角形的判定定理:(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????; (2)在Rt△ABC中,∠C=90度,∠A -∠B =30°,那么∠A=?????? ,∠B=?????? ;(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.(4)在直角三角形中,斜边及其中线之和
为6,那么该三角形的斜边长为________. 本节课我们学习了哪些内容?1:直角三角形两锐角互余;2:在直角三角形中,斜边上的中线等于斜边的一半;
……2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。3:有两个角互余的三角形是直角三角形; ……1、如图,在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的高,那么,
与∠B互余的角有????????,
与∠A互余的角有????????,
与∠B相等的角有????????? ,
与∠A相等的角有?????????.作业:
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
