湘教版数学九年级(新) 课件:4.3.1解直角三角形(共19张PPT)
文档属性
| 名称 | 湘教版数学九年级(新) 课件:4.3.1解直角三角形(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 209.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-14 16:55:00 | ||
图片预览



文档简介
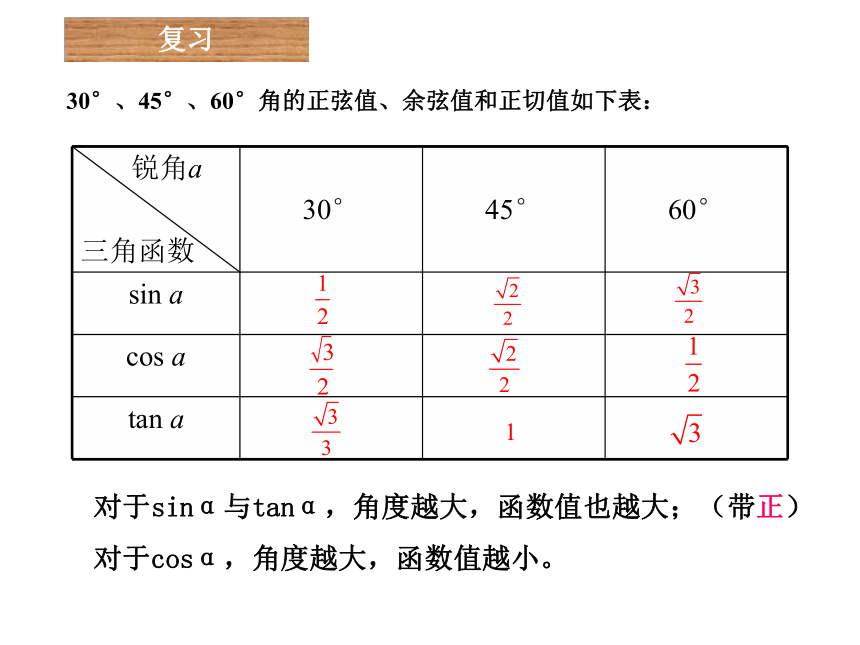
课件19张PPT。第四章 锐角三角函数4.3解直角三角形(1) 知 识回 顾一个直角三角形有几个元素?它们之间有何关系?(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=cosA=tanA=有三条边和三个角,其中有一个角为直角锐角三角函数复习30°、45°、60°角的正弦值、余弦值和正切值如下表:对于sinα与tanα,角度越大,函数值也越大;(带正)
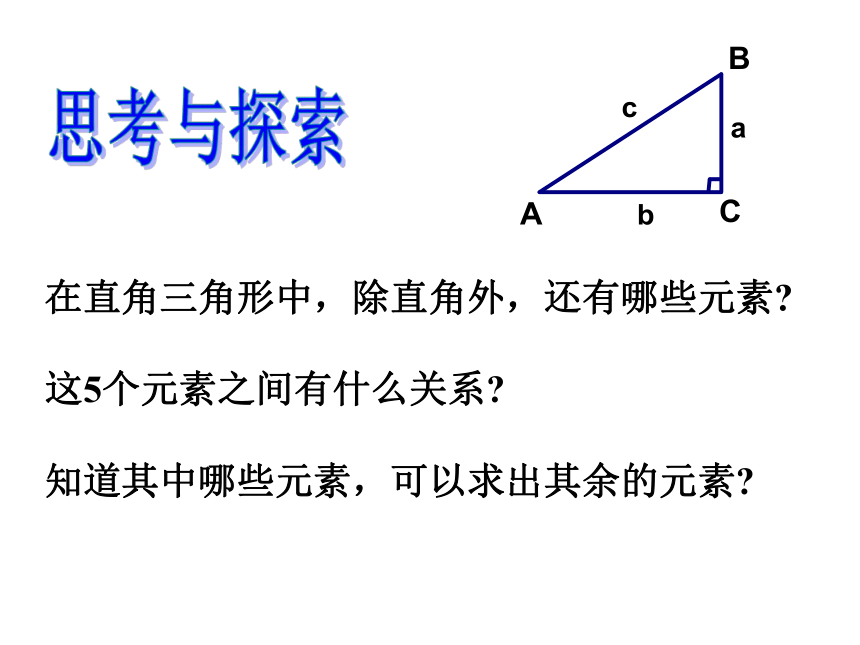
对于cosα,角度越大,函数值越小。在直角三角形中,除直角外,还有哪些元素?
这5个元素之间有什么关系?
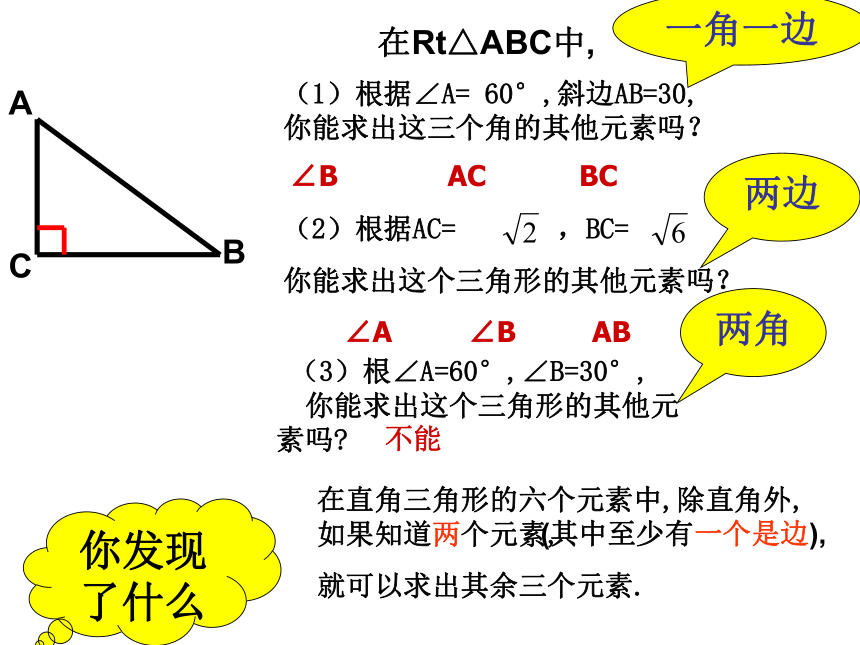
知道其中哪些元素,可以求出其余的元素?思考与探索在Rt△ABC中,(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A你发现了什么BC∠B AC BC∠A ∠B AB一角一边两边两角 (3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?不能如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有
哪些等量关系呢?
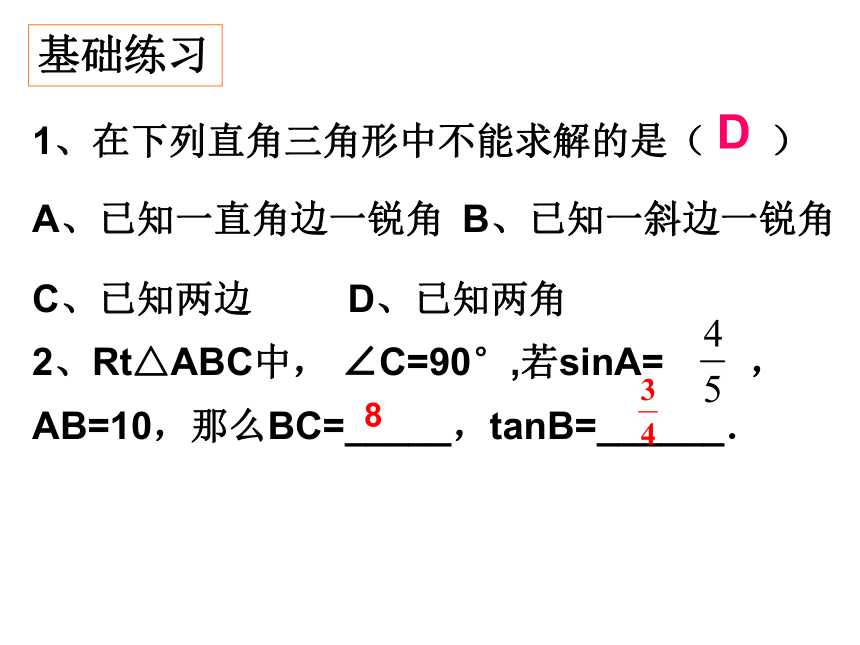
(1)两锐角关系 :∠ A+ ∠ B= 90o(2)三边关系:a2+b2=c2(勾股定理); (3)边与角关系:abc基础练习1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,那么BC=_____,tanB=______.D8例题分析
解:由勾股定理得:在Rt △ABC中,AB=2AC所以, ∠B=30° ∠A=60°?在Rt△ABC中,如果∠A=α,AC=x米,你能用α、x分别表示∠B、AB、BC吗?有斜用弦无斜用切∠B=90°-ααx1例题分析2、在Rt△ABC中,∠C=90°,∠B=60°,
b= .解这个直角三角形 .解:在Rt△ABC中,∠B=60°,b=
∴∠A=30°,c=2a方法一:设a=x,c=2x
由勾股定理得:∴c=8,a=4方法二:即:∴c=8方法一方法二比较这两种方法哪个方法更简单?如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形。6解:因为AD平分∠BAC变式: 如图,根据图中已知数据,求 △ABC其余各边的长,各角的度数和△ABC的面积.
75°ABC┓D⌒450如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求:AB的长; ⌒⌒60°6点睛:添加辅助线,“化斜为直”是我们常用的一种方法。再接再励例题分析3. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线AD= ,解这个直角三角形。6解:因为AD平分∠BAC基础练习3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.(1)c=8,∠A =60°;(4)a=1, ∠B=30°.在⊿ABC中,∠C=900,解直角三角形:(如图)CAB4.已知a,c.则通过 ,求 ∠A 已知∠A,a. 则b= c= a 3.已知∠A,b. 则a= 的2. 已知∠A,c. 则a= b= a 提高练习5.已知b,c.则通过 ,求 ∠A ∠A+ ∠ B=90°a2+b2=c2三角函数
关系式解直角三角形:由已知元素求未知元素的过程直角三角形中,已知一边一角如何解直角三角形?1.定义:解直角三角形
解直角三角形中,有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
2.直角三角形中的五个元素之间关系;
(1)有斜用弦,无斜用切.(2)数形结合,利于分析.(3)构造直角三角形.课堂小结3.解直角三角形中的几个注意:1已知斜边求直边,已知直边求直边,已知两边求一边,已知两边求一角,已知锐角求锐角,已知直边求斜边,计算方法要选择,正弦余弦很方便;正切余切理当然;函数关系要选好;勾股定理最方便;互余关系要记好;用除还需正余弦;能用乘法不用除.优选关系式1
对于cosα,角度越大,函数值越小。在直角三角形中,除直角外,还有哪些元素?
这5个元素之间有什么关系?
知道其中哪些元素,可以求出其余的元素?思考与探索在Rt△ABC中,(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A你发现了什么BC∠B AC BC∠A ∠B AB一角一边两边两角 (3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?不能如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有
哪些等量关系呢?
(1)两锐角关系 :∠ A+ ∠ B= 90o(2)三边关系:a2+b2=c2(勾股定理); (3)边与角关系:abc基础练习1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,那么BC=_____,tanB=______.D8例题分析
解:由勾股定理得:在Rt △ABC中,AB=2AC所以, ∠B=30° ∠A=60°?在Rt△ABC中,如果∠A=α,AC=x米,你能用α、x分别表示∠B、AB、BC吗?有斜用弦无斜用切∠B=90°-ααx1例题分析2、在Rt△ABC中,∠C=90°,∠B=60°,
b= .解这个直角三角形 .解:在Rt△ABC中,∠B=60°,b=
∴∠A=30°,c=2a方法一:设a=x,c=2x
由勾股定理得:∴c=8,a=4方法二:即:∴c=8方法一方法二比较这两种方法哪个方法更简单?如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形。6解:因为AD平分∠BAC变式: 如图,根据图中已知数据,求 △ABC其余各边的长,各角的度数和△ABC的面积.
75°ABC┓D⌒450如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求:AB的长; ⌒⌒60°6点睛:添加辅助线,“化斜为直”是我们常用的一种方法。再接再励例题分析3. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线AD= ,解这个直角三角形。6解:因为AD平分∠BAC基础练习3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.(1)c=8,∠A =60°;(4)a=1, ∠B=30°.在⊿ABC中,∠C=900,解直角三角形:(如图)CAB4.已知a,c.则通过 ,求 ∠A 已知∠A,a. 则b= c= a 3.已知∠A,b. 则a= 的2. 已知∠A,c. 则a= b= a 提高练习5.已知b,c.则通过 ,求 ∠A ∠A+ ∠ B=90°a2+b2=c2三角函数
关系式解直角三角形:由已知元素求未知元素的过程直角三角形中,已知一边一角如何解直角三角形?1.定义:解直角三角形
解直角三角形中,有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
2.直角三角形中的五个元素之间关系;
(1)有斜用弦,无斜用切.(2)数形结合,利于分析.(3)构造直角三角形.课堂小结3.解直角三角形中的几个注意:1已知斜边求直边,已知直边求直边,已知两边求一边,已知两边求一角,已知锐角求锐角,已知直边求斜边,计算方法要选择,正弦余弦很方便;正切余切理当然;函数关系要选好;勾股定理最方便;互余关系要记好;用除还需正余弦;能用乘法不用除.优选关系式1
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
