鸡兔同笼课件(共20张PPT)人教版四年级下册数学
文档属性
| 名称 | 鸡兔同笼课件(共20张PPT)人教版四年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 556.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-05 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
人教版 数学 四年级 下册
第九单元 数学广角
鸡兔同笼
今有雉兔同笼, 上有三十五头, 下有九十四足, 问雉兔各几何
疑学问思
我国古代数学名著《孙子算经》中记载一
道数学趣题—“鸡兔同笼”问题。
请你猜一猜,大概有多少只鸡, 多少只兔?
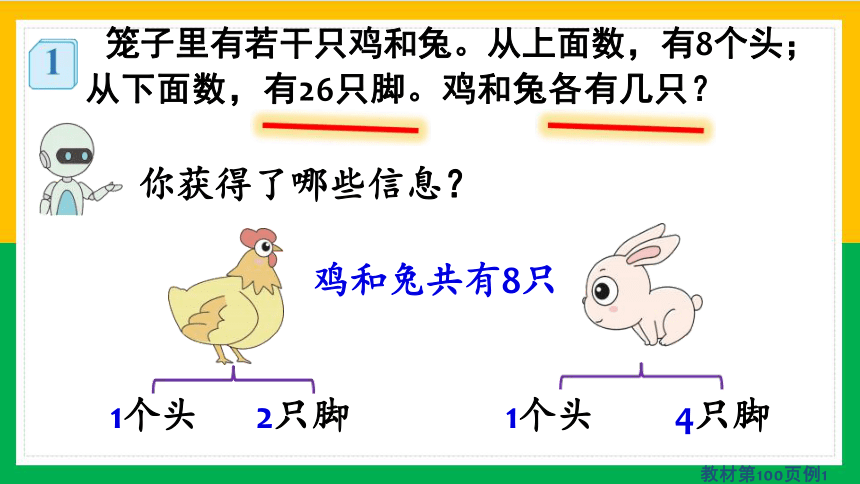
笼子里有若干只鸡和兔。从上面数,有8个头;
从下面数,有26只脚。鸡和兔各有几只?
你获得了哪些信息?
鸡和兔共有8只
1个头 2只脚 1个头 4只脚
教材第100页例1
组学辨思
合作学习要求:
1.独立思考,选择你喜欢的方法解决问题(可以 用画一画、写算式、列表格等方法)
2.小组内交流想法
用 表示头,用 表示脚。
如果用8个圈表示8个头,我来画一画脚......
我来画图
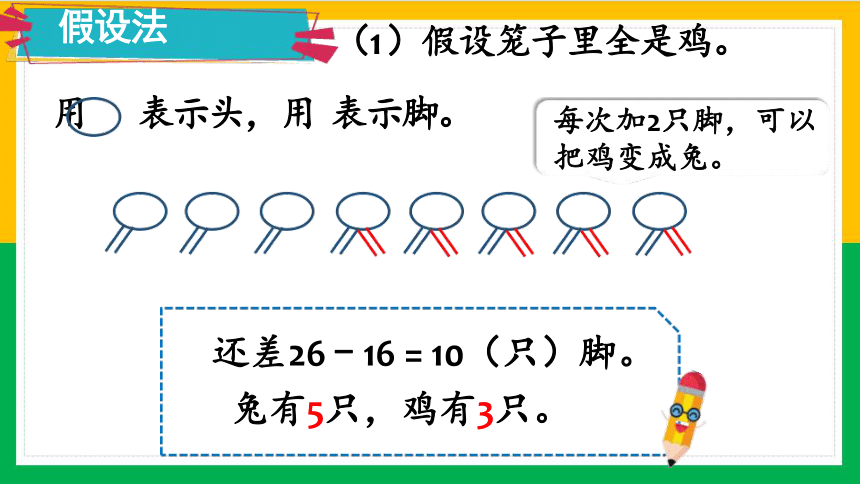
还差26 - 16 = 10(只)脚。 兔有5只,鸡有3只。
假设法 (1 )假设笼子里全是鸡。
每次加2只脚,可以 把鸡变成兔。
用 表示头,用 表示脚。
兔的只数:(26-8×2 ) ÷(4-2)
=10÷2 =5(只)
鸡的只数:8 - 5 = 3(只)
答:兔有5只,鸡有3只。
假设法
设鸡得兔法
(1 )假设笼子里全是鸡。
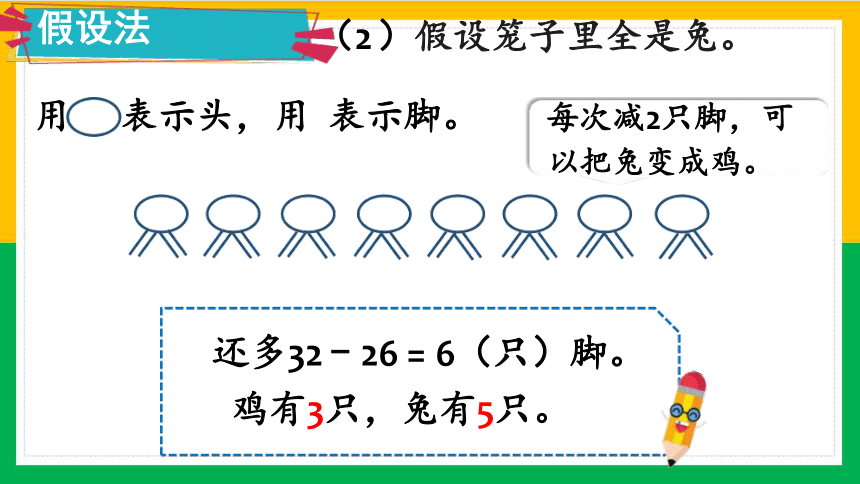
假设法 (2 )假设笼子里全是兔。
用 表示头,用 表示脚。 每次减2只脚,可
以把兔变成鸡。
还多32 - 26 = 6(只)脚。 鸡有3只,兔有5只。
鸡的只数:(8×4-26) ÷(4-2)
=6÷2 =3(只)
兔的只数:8 - 3 = 5(只)
答:兔有5只,鸡有3只。
假设法
设兔得鸡法
(2)假设笼子里全是兔。
当用假设法解决“鸡兔同笼”问题时,假
设全是鸡,先算出的是兔的只数;假设
全是兔,先算出的是兔的只数。
猜测法、画图法、和列表法效率低。对于数据较
大的“鸡兔同笼”问题,一般用假设法来解决。
兔的只数:( 94-35×2 ) ÷(4-2)
=24÷2 =12(只)
鸡的只数:35-12=23(只) 答:兔有12只,鸡有23只。
笼子里有若干只鸡和兔。从上面数,有35个头, 从下面数,有94只脚。鸡和兔各有几只?
你能用上面的方法解决前面的“鸡兔同笼”问题吗?
方法一:假设全是鸡
鸡的只数:( 35×4-94) ÷(4-2)
=46÷2 =23(只)
兔的只数:35-23=12(只) 答:兔有12只,鸡有23只。
笼子里有若干只鸡和兔。从上面数,有35个头, 从下面数,有94只脚。鸡和兔各有几只?
你能试着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法二:假设全是兔
龟的只数:( 112-40×2 ) ÷(4-2)
=32÷2 =16(只)
鹤的只数:40-16=24(只) 答:龟有16只,鹤有24只。
龟鹤问题
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟和鹤 各有几只?
方法一:假设全是鹤
拓学创思
鹤的只数:( 4 0×4-112) ÷(4-2)
=48÷2 =24(只)
龟的只数:40-24=16(只) 答:龟有16只,鹤有24只。
龟鹤问题
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟 和鹤各有几只?
方法二:假设全是龟
课堂练习
1.停车场上停有小轿车和摩托车一共32辆,这些车
一共有108个轮子。小轿车和摩托车各有多少辆?
方法一:假设32辆车全是摩托车
小轿车的数量:
(108-32×2) ÷(4-2)
=(108-64) ÷2
=44÷2
=22(辆)
摩托车的数量:32-22=10(辆)
课堂练习
1.停车场上停有小轿车和摩托车一共32辆,这些车
一共有108个轮子。小轿车和摩托车各有多少辆?
方法二:假设32辆车全是小轿车
摩托车的数量:
(32×4-108) ÷(4-2)
=(128-108) ÷2
=20÷2
=10(辆)
小轿车的数量:32-10=22(辆)
2.全班有54人去公园划船,一共租用了10只船,每只大 船坐6人,每只小船坐4人,且所有的船刚好坐满。租 用的大船和小船分别有多少只?
方法一:假设全是小船
大船的数量: (54-10 ×4) ÷(6-4)
=(54-40) ÷2
=14÷2
=7(只)
小船的数量:10-7=3(人)
答:租用的大船有7只,小船有3只。
2.全班有54人去公园划船,一共租用了10只船,每只大 船坐6人,每只小船坐4人,且所有的船刚好坐满。租 用的大船和小船分别有多少只?
方法二:假设全是大船
小船的数量: (10 ×6-54) ÷(6-4) =(60-54) ÷2
=6÷2 =3(只)
大船的数量:10-3=7(人)
答:租用的大船有7只,小船有3只。
3.某小学举办语文知识竞赛,共有10道抢答题,每 答对一道题加10分,答错一道题扣5分。壮壮同学在 这次竞赛中得了70分,他答对了几道题?
答对的数量:
(10×10-70) ÷(10+5)
=(100-70) ÷15
=30÷15
=2(道)
答对的数量:10-2=8(道)
学习评价
学习目标:
1.会用画图、 列表、 假设等方法解决 “鸡兔同笼”问题, 了解不同方法之间的联系和区别。
2.能够辨别除了 “鸡兔同笼”问题外 , 还有哪些问题也 算“鸡兔同笼”问题 , 并能用上面的方法灵活解决。
人教版 数学 四年级 下册
第九单元 数学广角
鸡兔同笼
今有雉兔同笼, 上有三十五头, 下有九十四足, 问雉兔各几何
疑学问思
我国古代数学名著《孙子算经》中记载一
道数学趣题—“鸡兔同笼”问题。
请你猜一猜,大概有多少只鸡, 多少只兔?
笼子里有若干只鸡和兔。从上面数,有8个头;
从下面数,有26只脚。鸡和兔各有几只?
你获得了哪些信息?
鸡和兔共有8只
1个头 2只脚 1个头 4只脚
教材第100页例1
组学辨思
合作学习要求:
1.独立思考,选择你喜欢的方法解决问题(可以 用画一画、写算式、列表格等方法)
2.小组内交流想法
用 表示头,用 表示脚。
如果用8个圈表示8个头,我来画一画脚......
我来画图
还差26 - 16 = 10(只)脚。 兔有5只,鸡有3只。
假设法 (1 )假设笼子里全是鸡。
每次加2只脚,可以 把鸡变成兔。
用 表示头,用 表示脚。
兔的只数:(26-8×2 ) ÷(4-2)
=10÷2 =5(只)
鸡的只数:8 - 5 = 3(只)
答:兔有5只,鸡有3只。
假设法
设鸡得兔法
(1 )假设笼子里全是鸡。
假设法 (2 )假设笼子里全是兔。
用 表示头,用 表示脚。 每次减2只脚,可
以把兔变成鸡。
还多32 - 26 = 6(只)脚。 鸡有3只,兔有5只。
鸡的只数:(8×4-26) ÷(4-2)
=6÷2 =3(只)
兔的只数:8 - 3 = 5(只)
答:兔有5只,鸡有3只。
假设法
设兔得鸡法
(2)假设笼子里全是兔。
当用假设法解决“鸡兔同笼”问题时,假
设全是鸡,先算出的是兔的只数;假设
全是兔,先算出的是兔的只数。
猜测法、画图法、和列表法效率低。对于数据较
大的“鸡兔同笼”问题,一般用假设法来解决。
兔的只数:( 94-35×2 ) ÷(4-2)
=24÷2 =12(只)
鸡的只数:35-12=23(只) 答:兔有12只,鸡有23只。
笼子里有若干只鸡和兔。从上面数,有35个头, 从下面数,有94只脚。鸡和兔各有几只?
你能用上面的方法解决前面的“鸡兔同笼”问题吗?
方法一:假设全是鸡
鸡的只数:( 35×4-94) ÷(4-2)
=46÷2 =23(只)
兔的只数:35-23=12(只) 答:兔有12只,鸡有23只。
笼子里有若干只鸡和兔。从上面数,有35个头, 从下面数,有94只脚。鸡和兔各有几只?
你能试着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法二:假设全是兔
龟的只数:( 112-40×2 ) ÷(4-2)
=32÷2 =16(只)
鹤的只数:40-16=24(只) 答:龟有16只,鹤有24只。
龟鹤问题
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟和鹤 各有几只?
方法一:假设全是鹤
拓学创思
鹤的只数:( 4 0×4-112) ÷(4-2)
=48÷2 =24(只)
龟的只数:40-24=16(只) 答:龟有16只,鹤有24只。
龟鹤问题
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟 和鹤各有几只?
方法二:假设全是龟
课堂练习
1.停车场上停有小轿车和摩托车一共32辆,这些车
一共有108个轮子。小轿车和摩托车各有多少辆?
方法一:假设32辆车全是摩托车
小轿车的数量:
(108-32×2) ÷(4-2)
=(108-64) ÷2
=44÷2
=22(辆)
摩托车的数量:32-22=10(辆)
课堂练习
1.停车场上停有小轿车和摩托车一共32辆,这些车
一共有108个轮子。小轿车和摩托车各有多少辆?
方法二:假设32辆车全是小轿车
摩托车的数量:
(32×4-108) ÷(4-2)
=(128-108) ÷2
=20÷2
=10(辆)
小轿车的数量:32-10=22(辆)
2.全班有54人去公园划船,一共租用了10只船,每只大 船坐6人,每只小船坐4人,且所有的船刚好坐满。租 用的大船和小船分别有多少只?
方法一:假设全是小船
大船的数量: (54-10 ×4) ÷(6-4)
=(54-40) ÷2
=14÷2
=7(只)
小船的数量:10-7=3(人)
答:租用的大船有7只,小船有3只。
2.全班有54人去公园划船,一共租用了10只船,每只大 船坐6人,每只小船坐4人,且所有的船刚好坐满。租 用的大船和小船分别有多少只?
方法二:假设全是大船
小船的数量: (10 ×6-54) ÷(6-4) =(60-54) ÷2
=6÷2 =3(只)
大船的数量:10-3=7(人)
答:租用的大船有7只,小船有3只。
3.某小学举办语文知识竞赛,共有10道抢答题,每 答对一道题加10分,答错一道题扣5分。壮壮同学在 这次竞赛中得了70分,他答对了几道题?
答对的数量:
(10×10-70) ÷(10+5)
=(100-70) ÷15
=30÷15
=2(道)
答对的数量:10-2=8(道)
学习评价
学习目标:
1.会用画图、 列表、 假设等方法解决 “鸡兔同笼”问题, 了解不同方法之间的联系和区别。
2.能够辨别除了 “鸡兔同笼”问题外 , 还有哪些问题也 算“鸡兔同笼”问题 , 并能用上面的方法灵活解决。
